Литвиненко А.В. Методы и средства защиты информации

Подождите немного. Документ загружается.

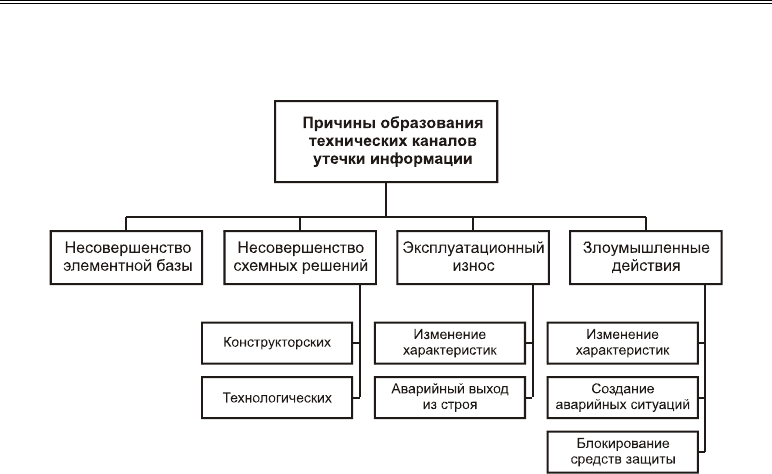
Технические каналы утечки информации. Классификация, причины и источники…

101

принятых для данной категории технических средств, эксплуатационный износ элемен-

тов изделия, а также злоумышленные действия.

Рис. 4.1. Классификация причин образования

технических каналов утечки информации

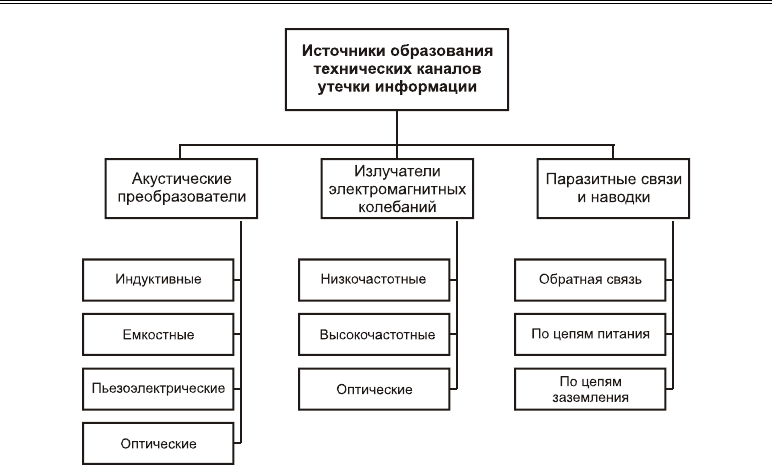
Основными источниками образования технических каналов утечки информации

(рис. 4.2) являются:

• преобразователи физических величин;

• излучатели электромагнитных колебаний;

• паразитные связи и наводки на провода и элементы электронных устройств.

Для каждой из этих групп, в свою очередь, можно выполнить декомпозицию по

принципу преобразования или иным параметрам. Так, по принципам преобразования

акустические преобразователи подразделяются на индуктивные, емкостные, пьезоэлек-

трические и оптические. При этом по виду преобразования они могут быть и акустиче

скими, и электромагнитными.

Декомпозиция излучателей электромагнитных колебаний выполняется по диапазону

частот.

102 Глава 4. Каналы несанкционированного получения информации

Рис. 4.2. Классификация источников образования

технических каналов утечки информации

Паразитные связи и наводки проявляются в виде обратной связи (наиболее характерна по-

ложительная обратная связь), утечки по цепям питания и заземления.

Технические средства и системы могут не только непосредственно излучать в про-

странство сигналы, содержащие обрабатываемую ими информацию, но и улавливать за

счет своих микрофонных или антенных свойств существующие в непосредственной

близости от них акустические либо электромагнитные излучения. Такие технические

средства могут преобразовывать принятые излучения в электрические сигналы и пере-

давать их по своим линиям связи, как правило, бесконтрольным, за территорией объекта

на значительные расстояния, что в еще большей степени повышает опасность

утечки

информации.

Возможностью образовывать подобные радиотехнические каналы утечки обладают

некоторые телефонные аппараты, датчики охранной и пожарной сигнализации, их ли-

нии, а также сеть электропитания.

Нередки случаи, когда технические устройства имеют в своем составе, помимо по-

добных “микрофонов” и “антенн”, высокочастотные или импульсные генераторы. Гене-

рируемые колебания в таких устройствах могут быть

промодулированы проявившимися

электрическими сигналами, вследствие чего эти технические устройства превращаются в

радиопередатчики и представляют серьезную опасность, так как способны излучать ин-

формацию в окружающее пространство.

Как в любой системе связи, в каналах утечки информации опасный сигнал (сигнал, не-

сущий секретную информацию) характеризуется длительностью

, динамическим диапа-

зоном

и шириной спектра F

, произведение которых представляет собой его объем V

= T

Технические каналы утечки информации. Классификация, причины и источники…

103

Чтобы принять такой объем информации, на принимающей стороне должна быть ап-

паратура, обладающая соответствующими характеристиками, т.е. имеющая необходи-

мую чувствительность при определенном превышении сигнала над уровнем собствен-

ных помех, и обеспечивающая необходимую ширину полосы принимаемых сигналов

при соответствующей длительности их передачи.

Очевидно, что по каналу может пройти без искажения лишь

такой сигнал, который

удовлетворяет условиям (

, F

и Д

— это длительность приема информации каналом,

ширина спектра принимаемого сигнала и динамический диапазон канала, соответствен-

но):

≤ Т

; F

≤ F

; Д

≤ Д

К основным информационным характеристикам канала относятся:

• местоположение начала и конца канала;

• форма передаваемой информации (дискретная, непрерывная) в звеньях канала;

• структура канала передачи (датчик, кодер, модулятор, линия, демодулятор, декодер,

устройство фиксации и др.);

• вид канала (телефонный, телеграфный, телевизионный и др.);

• скорость передачи и объем передаваемой информации;

• способы преобразования информации в звеньях канала передачи (методы модуляции,

кодирования и т.д.);

• пропускная способность канала;

• емкость канала.

Кроме того, классификация каналов передачи возможна по следующим признакам:

• по виду сигналов и способу передачи;

• по исполнению: проводные, кабельные, световодные, радио и другое;

• по принципу действия: электромагнитные, оптические, акустические.

Параметры канала определяются физической структурой канала, его типом и режи-

мом использования.

Ширина полосы пропускания (частотный спектр) канала

F меняется от 3100 Гц для

телефонного до 8 МГц для телевидения и до сотен мегагерц для оптических линий свя-

зи.

Превышение сигнала над помехой в канале (динамический диапазон)

Д, определяе-

мое соотношения мощностей сигнала и помехи в канале, — способность канала переда-

вать различные уровни сигнала. Этот параметр связан с расчетным уровнем помех, воз-

можностями модуляции. Динамический диапазон

Д ограничивает дальность передачи, а

также влияет на возможность выделения сигнала на фоне помех. Дальность определяет-

ся выражением:

Д = log (Р

/ Р

104 Глава 4. Каналы несанкционированного получения информации

где Р

и Р

— средние мощности, соответственно, сигнала и помехи в канале на входе

приемника.

Каждый канал также характеризуется количеством информации, которое может быть

передано по нему.

Предельное значение количества информации, которое может быть передано по

каналу связи, обладающему полосой пропускания

, определяется формулой Шенно-

на:

max

= F

log (1 + Р

/ Р

) [дв. ед./с],

где Р

— средняя мощность сигнала, Р

— мощность шумов с равномерным частотным

спектром.

Сигнал и его описание

Основным элементом рассмотренных каналов утечки информации являются сигна-

лы, совокупность которых, в свою очередь, формирует информационное сообщение.

Сообщение может иметь дискретную природу, т.е. состоять из отдельных символов. В

этом случае и сигнал составляется из отдельных элементов, и представляет собою дис-

кретную последовательность. Примером может служить передача текста по телеграфу.

Сообщение

может представлять собою и непрерывную функцию времени. В про-

стейшем случае эта функция непосредственно используется в качестве сигнала. Так об-

стоит, например, дело при обычной городской телефонной связи. Для передачи на

большие расстояния прибегают к модуляции, к которой и сводится образование сигнала.

Если же при передаче используется непрерывная функция с

импульсными или кодо-

выми методами, то нужно произвести дискретизацию функции по времени, т.е. перейти

от функции непрерывного аргумента к функции дискретного аргумента. Эта операция

выполняется путем взятия отсчетов функции в определенные дискретные моменты

. В

результате функция

m(t) заменяется совокупностью мгновенных значений

{ m

} = { m(t

) }.

Обычно моменты отсчетов располагаются по оси времени равномерно, т.е.

= k Δt.

Выбор интервала Δt производится на основании теоремы Котельникова, которая

гласит:

функция с ограниченным спектром полностью определяется своими значениями, от-

считанными через интервалы

Δt = ½ F,

где F — ширина спектра.

Это положение может применяться и к функциям с неограниченным, но быстро убы-

вающим за пределами интервала

F спектром. В таком случае функция восстанавливается по

своим отсчетам не точно, но с легко оцениваемым приближением.

Сигнал и его описание 105

Исходное сообщение может представлять собой функцию не одного, а многих аргу-

ментов. В этом случае такая функция превращается в функцию

m(t), зависящую от од-

ного аргумента. Это осуществляется посредством операции, называемой разверткой.

При этом может произойти дискретизация по одному, нескольким или всем аргументам.

Примером может послужить образование телевизионного сигнала. Изображение может

быть представлено как

B(x, y, t), где x и y — пространственные координаты (координа-

ты плоскости изображения),

B — яркость. Время дискретизируется в результате покад-

ровой передачи (

Δt = 1/25 с). При обычной строчной развертке координата x (вдоль

строки) остается непрерывной, а координата

y дискретизируется. Шаг Δy определяется

количеством строк развертки. Таким образом, получается функция

m(t) = m(iΔy, kΔt, vt),

где v — скорость развертки вдоль строки, i — номер строки, k — номер кадра.

До сих пор речь шла о дискретизации по аргументам. Но возможна (а иногда необхо-

дима) дискретизация по значениям функции. Предполагается, что функция ограничена,

т.е. ее значения лежат в конечном интервале. В таком случае дискретизация состоит в

замене несчетного множества возможных значений функции конечным множеством.

Обычно дискретные значения

располагаются по шкале функции равномерно, так что

= [m/Δm + ½] Δm,

где скобки обозначают функцию выделения целой части, Δm — шаг квантования.

Понятно, что квантование, заменяющее истинное значение

m округленным значени-

ем

, вносит погрешность ε = m – m

Однако существенно, что эта погрешность не превосходит половины шага квантова-

ния и, следовательно, находится под нашим контролем.

Итак, при импульсной передаче необходима дискретизация по времени, а при кодо-

вой передаче, кроме того, и дискретизация по значениям функции, т.е. квантование.

Рассмотрим вопросы модуляции. Берется некоторая функция

f = f(a, b, c, ..., t),

называемая переносчиком. Величины a, b, c, ... представляют собой в отсутствие моду-

ляции постоянные параметры.

Сущность модуляции состоит в том, что один из параметров получает приращение,

пропорциональное передаваемому сообщению, например

a = a

+ δa = a

+ Δa m(t) = a

(1 + (Δa/a

) m(t)),

где δa — переменное приращение, Δa — постоянная величина, выражающая степень

изменения параметра. Если

|m(t)| ≤ 1, то отношение Δa/a

есть наибольшее относитель-

ное изменение параметра

a, или глубина модуляции.

Таким же образом может изменяться и любой другой параметр. Если изменяется

(модулируется) параметр

a, то мы имеем a-модуляцию, если параметр b — b-

модуляцию и т.д. Количество возможных видов модуляции при данном переносчике

106 Глава 4. Каналы несанкционированного получения информации

равно количеству его параметров. Так, например, если в качестве переносчика выбрано

синусоидальное колебание

f(t) = A sin (ωt + ψ),

то параметрами являются амплитуда A, частота ω и начальная фаза ψ. Каждый из этих

параметров можно модулировать, в результате чего получается, соответственно, ампли-

тудная (АМ), частотная (ЧС) и фазовая модуляция ФМ.

Если переносчиком является периодическая последовательность импульсов опреде-

ленной формы, параметрами являются: амплитуда, длительность, частота следования и

фаза. Это дает четыре основные вида импульсной модуляции: амплитудно-импульсная

(АИМ), длительностно-импульсная (ДИМ

), частотно-импульсная (ЧИМ) и фазово-

импульсная (ФИМ). Переход от видеоимпульсов к радиоимпульсам позволяет получить

еще два вида модуляции: по частоте и по фазе высокочастотного заполнения.

Возможны, в принципе, многочисленные виды модуляции по параметрам, опреде-

ляющим форму видеоимпульсов; однако на практике такие виды модуляции пока не

применяются.

В качестве переносчика можно

воспользоваться не только периодической функцией,

но и стационарным случайным процессом. В этом случае в качестве модулируемого

параметра можно взять любую числовую характеристику, которая в силу стационарно-

сти является, по определению, постоянной (т.е. не зависящей от начала отсчета времени)

величиной. Таковы, например, моменты распределения или их Фурье-преобразования.

Первый момент, т

.е. среднее значение, обычно равен нулю. Второй момент есть функция

корреляции, зависящая от временного сдвига

τ. Фурье-преобразование функции корре-

ляции есть спектр мощности. Второй момент при

τ = 0 есть просто мощность. Модуля-

ция по мощности представляет собой аналогию амплитудной модуляции. Модуляция по

положению спектра на шкале частот в чем-то подобна частотной модуляции. Аналога

фазовой модуляции для случайного процесса не существует.

Следует иметь в виду, что мощность, определенная для конечного отрезка реализа-

ции случайного процесса, есть случайная величина, флуктуирующая

около среднего

значения. Тоже относится и к любым другим моментам или их преобразованиям. По-

этому при использовании случайного процесса в качестве переносчика в сигнал с самого

начала примешивается специфическая помеха, хотя и не устранимая, но с известными

статистическими характеристиками.

Сигналы с помехами

Наряду с полезным сигналом на вход приемника, как правило, действует помеха.

Обычно сигнал и помеха взаимодействуют между собой аддитивно, т.е. суммируются.

Иногда между ними имеет место и мультипликативное взаимодействие. Таким образом,

при достаточно сильных помехах прием полезного сигнала может значительно затруднит-

ся или вообще стать невозможным. Поэтому для обеспечения необходимого

качества

приема необходимо каким-то образом устранить или ослабить воздействие помехи на

средство приема.

Сигналы с помехами 107

Исследуем влияние помехи на основные характеристики сигнала при аддитивном их

взаимодействии в трех основных случаях.

1. Если сигнал х(t) и помеха х

(t) являются квазидетерминированными, то суммарный

сигнал

(t) = х(t) + х

(t). Предположим, что х(t) и х

(t) — импульсы. Тогда спектр

суммарного сигнала

(iω) = S(iω) + S

(iω),

где S(iω) и S

(iω) спектры соответственно х(t) и х

(t).

Энергия суммарного сигнала будет описываться следующим выражением:

⌡

⌠

–∞

+∞

(t) dt = E

+ E

+ 2E

⌡

⌠

–∞

+∞

(t) dt +

⌡

⌠

–∞

+∞

(t) dt + 2

⌡

⌠

–∞

+∞

х(t)x

(t) dt ,

где E

— энергия взаимодействия сигнала и помехи.

Если

= 0, то сигнал и помеха ортогональны. Корреляционная функция суммар-

ного сигнала в этом случае имеет следующий вид:

(τ) =

⌡

⌠

–∞

+∞

(t) х

(t – τ)dt = R

(τ) + R

(τ)

(0) + R

(0) = E

Если сигнал является квазидетерминированным, а помеха случайной, то суммарный

сигнал, описываемый выражением

(t) = х(t) + х

(t), может рассматриваться, как

нестационарный сигнал, у которого математическое ожидание является функцией

времени. Сигнал и помеха в этом случае взаимонезависимы, поэтом корреляционная

функция суммарного сигнала

(τ) = R

(τ) + R

(τ)

Если сигнал периодический, то

(τ) является периодической функцией, а R

(∞) =

. Это используется для выделения периодического сигнала из случайной помехи.

Если сигнал и помеха являются случайными, то

(t) = X(t) + X

(t). В этом случае

плотность вероятности

(x) сигнала X

(t) будет равна свертке распределений p(x)

p(х

Корреляционная функция суммарного сигнала:

(τ) = R

(τ) + R

(τ) + …

Если X(t) и X

(t) некоррелированы, то

(τ) = 0 и R

(τ) = 0

Тогда

(τ) = R

(τ) + R

(τ)

108 Глава 4. Каналы несанкционированного получения информации

Энергетический спектр суммарного сигнала

(ω) =

⌡

⌠

–∞

+∞

(τ) e

–jωτ

dτ = G

(ω) + G

(ω) + …

Если X(t) и X

(t) некоррелированы, то

(ω) = G

(ω) = 0

Способы борьбы с помехами в значительной мере зависят от их спектра. По относи-

тельному спектральному составу различают следующие три вида помех:

• высокочастотная с периодом повторений Т

значительно меньше времени измерения

изм

;

• с периодом повторения, близким к Т

изм

;

• низкочастотная с периодом повторения Т

, значительно превышающим Т

изм

Высокочастотную составляющую наиболее целесообразно уменьшать усреднением,

если при этом обеспечивается необходимое быстродействие приема информации.

Составляющая с периодом

≈ T

изм

часто представляет собой помехи с частотой се-

ти. В этом случае помехи уменьшают, применяя фильтры, интегрирование за время,

кратное периоду помехи, и осуществляя синфазирование моментов получения информа-

ции и перехода помехи через нулевое значение.

Низкочастотная составляющая устраняется обычно способами, разработанными для

систематических погрешностей.

Излучатели электромагнитных колебаний

Источниками опасного сигнала являются элементы, узлы и проводящие цепи техни-

ческих средств с токами и напряжениями опасных сигналов, а также голосовой аппарат

человека и элементы технических средств, создающие акустические поля опасных сиг-

налов.

К основным техническим системам и средствам относятся средства, предназначен-

ные для передачи, приема, обработки и хранения информации с

ограниченным доступом

(ИсОД):

• электронно-вычислительные машины (ЭВМ), в том числе персональные (ПЭВМ);

• аппаратура звукозаписи, звуковоспроизведения и звукоусиления;

• системы оперативно-командной и громкоговорящей связи;

• системы внутреннего телевидения;

• средства изготовления и размножения документов.

Вспомогательные технические системы и средства не предназначены для обработки

ИсОД, но при совместной установке с основными техническими системами и средства-

ми или при установке в служебных помещениях, где ведутся переговоры или работы,

связанные с ИсОД, они могут способствовать утечке информации или образовывать

“самостоятельные” системы утечки.

Излучатели электромагнитных колебаний 109

К вспомогательныем техническим системам и средствам относятся:

• системы открытой телефонной связи;

• системы радиотрансляции;

• системы электропитания;

• системы охранной и пожарной сигнализации.

Вспомогательные технические средства, а также различного рода цепи, расположенные

в непосредственной близости от основных технических систем и средств, могут обладать

антенным эффектом. Этот эффект заключается в преобразовании энергии приходящей от

основных технических систем и средств электромагнитной волны в энергию электриче-

ских токов. Вторичные технические системы и

средства, а также образовываемые ими це-

пи, называются также случайными приемными антеннами. К сосредоточенным случай-

ными приемным антеннам относятся телефонные аппараты, электрические звонки, датчи-

ки охранной и пожарной сигнализации и т.п. К распределенным случайным антеннам

относятся различного рода кабели, провода систем сигнализации, ретрансляционные сети,

трубы, металлические конструкции и т.

п.

При прохождении опасных сигналов по элементам и цепям технических средств, со-

единительным линиям, в окружающем пространстве возникает электромагнитное поле.

Поэтому такие средства и линии можно считать излучателями. Все источники опасного

сигнала принято рассматривать как излучатели, условно подразделяемые на три типа:

точечные, линейные (распределенные) и площадные.

Точечные излучатели — это технические средства

или излучающие элементы их

электрических схем, размеры которых значительно меньше длины волны опасного сиг-

нала, обрабатываемого технической системой и средством, и расстояния до границы

контролируемой зоны.

К распределенным излучателям относят кабельные и соединительные проводные

линии.

Площадные излучатели — это совокупность технических средств, равномерно рас-

пределенных на некоторой площади и обтекаемых одним

и тем же током.

Технические средства, для которых характерна большая амплитуда напряжения

опасного сигнала и малая амплитуда тока, относятся к электрическим излучателям. Тех-

нические средства с большой амплитудой тока и малой амплитудой напряжения рас-

сматриваются, как магнитные излучатели.

Кроме того, электромагнитные излучения радиоэлектронного оборудования (РЭО)

можно разделить на основные и нежелательные

Основные радиоизлучения характеризуются:

• несущей частотой;

• мощностью (напряженностью) поля;

• широкой полосой излучаемых частот;

• параметрами модуляции.

Нежелательные излучения подразделяются на побочные, внеполосные и шумовые.

110 Глава 4. Каналы несанкционированного получения информации

Наиболее опасными, с точки зрения образования каналов утечки информации, яв-

ляются побочные излучения.

Побочные излучения — это радиоизлучения, возникающие в результате любых не-

линейных процессов в радиоэлектронном устройстве, кроме процессов модуляции. По-

бочные излучения возникают как на основной частоте, так и на гармониках, а также в

виде их взаимодействия. Радиоизлучение на гармонике — это излучение на частоте (час-

тотах), в целое число раз большей частоты основного

излучения. Радиоизлучение на суб-

гармониках — это излучение на частотах, в целое число раз меньших частоты основного

излучения. Комбинационное излучение — это излучение, возникающее в результате взаи-

модействия на линейных элементах радиоэлектронных устройств колебаний несущей

(основной) частоты и их гармонических составляющих.

Отмечая многообразие форм электромагнитных излучений, следует подчеркнуть, что

имеется и так

называемое интермодуляционное излучение, возникающее в результате

воздействия на нелинейный элемент высокочастотного (ВЧ) тракта радиоэлектронной

системы (РЭС) генерируемых колебаний и внешнего электромагнитного поля.

Каждое электронное устройство является источником магнитных и электромагнит-

ных полей широкого частотного спектра, характер которых определяется назначением и

схемными решениями, мощностью устройства, материалами, из которых оно изготовле-

но,

и его конструкцией.

Известно, что характер поля изменяется в зависимости от расстояния до приемного

устройства. Если это расстояние значительно меньше длины волны электромагнитного

сигнала (

r<<λ), поле имеет ярко выраженный магнитный (или электрический) характер,

а в дальней зоне (

r>>λ) поле носит явный электромагнитный характер и распространя-

ется в виде полосной волны, энергия которой делится поровну между электрической и

магнитной компонентами.

Коль скоро длина волны определяет расстояние и тем более назначение, устройство,

принцип работы и другие характеристики правомерно подразделять излучатели элек-

тромагнитных сигналов на низкочастотные, высокочастотные и оптические.

Низкочастотные излучатели

Низкочастотными (НЧ) излучателями электромагнитных колебаний в основном явля-

ются звукоусилительные устройства различного функционального назначения и конструк-

тивного исполнения. В ближней зоне таких устройств наиболее мощным выступает маг-

нитное поле опасного сигнала. Такое поле усилительных систем достаточно легко обнару-

живается и принимается посредством магнитной антенны и селективного усилителя

звуковых частот (рис. 4.3).