Литейное производство 2011 № 1 январь

Подождите немного. Документ загружается.

ЛИТЕЙНОЕ ПРОИЗВОДСТВО№1/2011

пециальные способы литья

тичном кожухе, в котором находится

форма, создается разрежение, за

счет которого расплав поднимается

по металлопроводу и заполняет по-

лость формы. Схема процесса при-

ведена на рис. 4.

Несмотря на то, что все эти спо-

собы литья позволяют полностью

автоматизировать процесс изготов-

ления отливок и получать отливки

повышенного качества, широкого

распространения в нашей стране

они не получили. Это связано, с

одной стороны, с отсутствием обо-

рудования, а с другой, тем, что нет

анализа преимуществ того или ино-

го способа, с точки зрения получе-

ния качественных заготовок разной

конфигурации.

Для сравнительных испытаний

каждым из указанных способов

последовательно изготовляли от-

ливки в виде плиты 200×200×25

мм из сплава АК12, при одинаковых

температурах расплава (680°C) и

формы (200°C). Формы заполняли

при одинаковых параметрах (пере-

паде давления и скорости нараста-

ния давления). Таким образом, раз-

ницу в результатах получали только

за счет разницы в технологической

схеме изготовления отливок. Для

экспериментов использовали ли-

тейную машину ВИД-13, на которой

можно произвести все необходи-

мые исследования. Результаты ме-

ханических испытаний приведены в

таблице.

Способ литья Образец

, МПа

, МПа δ, %

Значения Среднее

ЛНД

229

222 150 7,5

212

224

223

ЛНД с р = 0,4 атм

237

225 158 7,0

211

208

226

ЛПрД

245

235 155 7,3

222

243

229

ЛНД в ВФ

250

233 160 6,9

225

238

220

ЛВВ с р = 0,4 атм

260

246 153 7,2

235

247

240

ЛВВ

244

231 152 7,1

227

230

224

По результатам испытаний можно

сделать следующие выводы:

• для всех исследуемых спосо-

бов литья избыточное давление в 0,4

атм приводит к повышению механи-

ческих свойств;

• самый высокий предел про-

чности получен при ЛВВ (246 МПа),

при ЛПрД, в ВФ и ЛНД, соответс-

твенно, 235; 233; 225 МПа;

Сведения об авторах

Алексей Геннадьевич Меркушев, О

АО “УралНИТИ”, (343) 355-25-98, ptlp@uralniti.ru;

Михаил Викторович Быстров, ОАО “УралНИТИ”, (343) 355-25-98, ptlp@uralniti.ru.

• по пределу текучести образ-

цы во всех рассматриваемых видах

литья различаются незначительно и

находятся в пределах 150…160 МПа;

• относительное удлинение для

всех видов литья повышенное и на-

ходится в пределах 6,9…7,5%;

• при литье в ВФ и при ЛВВ

заполняемость лучше, чем при

ЛНД и ЛПрД.

ЛИТЕЙНОЕ ПРОИЗВОДСТВО №1/2011

пециальные способы литья

Аннотация

The Summary

Положение о более эффективном удалении НМВ из

жидкого металла в условиях ц ентробежного ли-

тья (ЦЛ), по сравнению с другими способами, одно из

ведущих в современной теории центробежного литья,

основано на законе Архимеда, согласно которому вы-

талкивающая сила, действующая на погруженное в жид-

кость тело, равна равнодействующей сил, приложенных

к элементарным объемам вытесненной телом жидкости.

Поскольку центробежные силы, действующие во враща-

емом расплаве, больше сил тяжести, действующих при

обычном литье, то и выталкивающая сила будет больше.

Отсюда, казалось бы, очевидный вывод о более эффек-

тивном удалении НМВ из расплава в условиях ЦЛ. Авто-

ры монографии по ЦЛ [1], рассматривая эффективность

удаления НМВ, утверждают, что скорость их всплытия при

УДК 621.74.042

Е.К. Иванько

E.K. Ivanko

О динамике всплытия

неметаллических включений в

расплаве при центробежном литье

Dynamic Factors Emergings Of Non-

metallic Inclusions in Liquid Metal in

Conditions of Centrifugal Moulding

ЦЛ больше, чем при обычном, в √К раз, где K – гравита-

ционный коэффициент, что глубоко укоренилось в теории

ЦЛ. Но обратимся к практике.

Постановка вопроса. Исходя из приведенных в мо-

нографии формул, следует ожидать, что в условиях ЦЛ

максимальная скорость всплытия наиболее распростра-

ненных силикатных включений ∅ 0,1 мм, плотностью при

скорости вращения ρ = 4100 кг/м

, формы с К = 100 на

свободной поверхности расплава ρ = 6900 кг/м

, должна

составить 0,25 м/с, а при К = 50 – 0,11 м/с. Если учесть,

что скорость продвижения фронта кристаллизации метал-

ла, как правило, на два порядка ниже, следует ожидать

высокого уровня рафинирования металла при ЦЛ. Одна-

ко на практике эти ожидания, увы, не подтверждаются. В

ЦЛ-металле обнаруживаются НМВ размером не только

В работе рассмотрены, на основе законов гидродинамики, динамические факто-

ры, действующие на н еметаллические включения (НМВ) при их всплы-

тии в жидком металле в условиях центробежного литья. Показано, что всплытие

НМВ происходит не только под действием центробежных сил, но и возникающих

при этом тангенциальных сил. Движение НМВ происходит не в радиальном на-

правлении, как принято считать, а по более сложной траектории, имеющей тан-

генциальную составляющую. Рассмотрено влияние формы НМВ на их всплытие.

Ключевые слова

Неметаллические включения, центробежное литье, гидродинамика, жидкий металл

In work are considered, on the basis of laws of hydrodynamics, the dynamic factors

influencing nonmetallic inclusions at their emerging in liquid metal in conditions of

centrifugal moulding. It is shown, that emerging of nonmetallic inclusions occurs not

only under action of centrifugal forces, but also, arising at emerging, tangential forces.

Movement of nonmetallic inclusions occurs not in a radial direction as is standard to

count, and on more complex trajectory having a tangential component. Influence of the

form of nonmetallic inclusions on their emerging is considered.

Key words

Nonmetallic inclusions, centrifugal moulding, hydrodinamics, liquid metal

ЛИТЕЙНОЕ ПРОИЗВОДСТВО№1/2011

пециальные способы литья

0,1 мм, но и значительно большие. Почему же, вопреки

теоретическим расчетам, НМВ не всплыли? Действи-

тельно ли центробежные силы обеспечивают увеличение

скорости всплытия НМВ в √К раз и гарантируют более

эффективное их удаление?

В ЦЛ-металле обнаруживаются не только отдельные

НМВ, но и их скопления вытянутой формы. Такая не-

обычная их форма создала в литейной практике серьез-

ную проблему при количественной их оценке, поскольку

шкалы по ГОСТ 1778-80, предназначенные для обычного

металла, не имеют эталонов скоплений такой формы. В

80-е гг. в НПО «ЦНИИТМАШ» при разработке специаль-

ных шкал для ЦЛ-металла выяснили, что их вытянутость

ориентирована по окружности [2]. Почему? Согласно сов-

ременным представлениям [1], при ЦЛ устанавливается

«состояние относительного покоя» жидкого металла, то

есть всплытие НМВ происходит в тех же условиях, что и

при обычном литье. Отличие – в действии центробежных

сил. Но центробежные силы действуют в радиальном на-

правлении и не могут вытянуть скопления НМВ в танген-

циальном. Очевидно, что в вопросе удаления НМВ теория

ЦЛ практикой не подтверждается.

Несостоятельность существующих теорети-

ческих положений. В соо

тветствии с гидродинамикой,

всякому движению тела в жидкости противодействует со-

противление жидкости. Всплытие тела – частный случай

его движения под действием выталкивающей силы F

которой противодействует сопротивление жидкости F

. В

общем случае, уравнение движения всплывающего тела

будет иметь вид:

– F

= 0. (1)

Определить F

, как правило, несложно по закону Архи-

меда в условиях действия центробежных сил:

= Vω

r(ρ

– ρ

) = VKg(ρ

– ρ

), (2)

где V – объем НМВ плотностью ρ

; ω – угловая ско-

рость вращения жидкого металла плотностью ρ

; r – ра-

диус вращения; g – ускорение свободного падения.

А вот определение F

– сложная задача в гидроди-

намике. Как правило, ее определяют экспериментально.

Но авторы монографии, упростив решение, использо-

вали известные формулы для расчета всплытия НМВ с

наибольшим ∅ 0,1 мм в обычных условиях, применив

формулу Стокса, которая позволяет определить силу со-

противления жидкости на медленно движущееся в ней

шаровидное тело. Формула Стокса имеет вид [3]:

= 6πηRu, (3)

где R – радиус тела; u – скорость всплытия тела; η

– динамический коэффициент вязкости жидкости.

Подставив в уравнение движения (1) значения F

и F

найденные по формулам (2) и (3), соответственно, и ре-

шив его относительно u, получили формулу:

max

(ρ

– ρ

)

18η

(4)

где d – диаметр шарообразного включения.

Но формула Стокса справедлива лишь при Re << 1

(Re = uRρ/η) [3]. Приведенные выше расчеты по формуле

(4) скорости всплытия силикатных включений ∅ 0,1 мм

показывают, что при таких скоростях Re = 11,25. Отсюда

вывод: применение формулы (4) в условиях ЦЛ возмож-

но лишь при расчете для НМВ < ∅ 0,01 мм и непримени-

мо для включений ∅ 0,1 мм. Однако такие мелкие НМВ

всплывают не только по законам гидродинамики, но зави-

сят и от их поверхностных свойств, поскольку составляют

с расплавом коллоидную (микрогетерогенную) систему, в

которой процесс седиментации (осаждения) протекает под

воздействием межфазного натяжения на границе расплав

– НМВ. Таким образом, формула (4) несостоятельна для

условий ЦЛ.

Для расчета всплытия НМВ размером > 0,1 мм авторы

монографии предлагают использовать формулу, которая

основана на известной в гидродинамике формуле опре-

деления F

при турбулентном обтекании жидкостью шаро-

образного тела, которая отличается от известной формулы

Ньютона-Риттингера [4], определяющей скорость всплы-

тия включений сферической формы в обычных условиях

лишь входящим в нее гравитационным коэффициентом

K. На этой основе авторы сделали вывод об увеличении

этой скорости в условиях ЦЛ в √K раз. Так, рассчитан-

ная по формуле Ньютона-Риттингера, в условиях обыч-

ного литья, эта скорость достигает 0,025 м/с, а по вновь

предложенной формуле, в условиях ЦЛ, при K = 100, она

равна 0,25 м/с. Но достигает ли силикатное включение

таких больших скоростей? Практика ЦЛ говорит, что нет.

Почему?

Предложенная формула лишь позволяет определить

максимально возможную скорость при турбулентном

обтекании НМВ жидким металлом, которую НВМ может

и не достигнуть.

Динамика всплытия твердых тел в жидкости.

Изменение кинетических характеристик взаимодействия

между твердыми телами не влечет за собой изменения

самого механизма их взаимодействия. Иное взаимодейс-

твие – между твердым телом и жидкостью. Всплытие

твердого тела в жидкости под воздействием выталкиваю-

щей силы начинается из его неподвижного, по отношению

к жидкости, состояния и происходит с ускорением. Внача-

ле, когда движение тела медленное, сопротивление жид-

кости определяется ее вязкостью и, если тело шаровид-

ной формы, подчиняется закону Стокса. При увеличении

скорости всплытия между телом и жидкостью появляется

пограничный слой, которым также начинает определяться

сопротивление жидкости. На поверхности всплывающего

ЛИТЕЙНОЕ ПРОИЗВОДСТВО №1/2011

пециальные способы литья

тела скорость жидкости равна скорости всплытия тела, ко-

торое вовлекает в движение жидкость, и та, за счет инер-

ции, увеличивает силу сопротивления. Влияние толщины

пограничного слоя на силу сопротивления учитывается в

формулах в виде присоединенной массы.

С дальнейшим увеличением скорости всплытия тела

толщина пограничного слоя уменьшается. Ламинарный

характер обтекания жидкостью всплывающего тела пере-

ходит в турбулентный, что изменяет механизм сопротив-

ления жидкости всплытию тела и приводит к увеличению

градиента скорости на поверхности тела и коэффициен-

та трения, что становится превалирующим фактором в

создании сопротивления всплытию. Скорость всплытия

растет до тех пор, пока тело не достигнет уравновешен-

ного состояния, то есть пока выталкивающая тело сила

уравновесится силами сопротивления жидкости, и тогда

тело начинает всплывать с постоянной скоростью, кото-

рую называют максимальной. Она может наступить как на

стадии сопротивления жидкости только за счет вязкости

с появления пограничного слоя, так и на стадии турбули-

зации.

Сложная, изменяющаяся динамика всплытия тела в

жидкости порождает необходимость в каждом конкрет-

ном случае определять механизм сопротивления жид-

кости движению тела, при котором наступает его уравно-

вешенное состояние. Приняв для расчета свою формулу,

авторы монографии должны были обосновать, что ско-

рость всплытия НМВ достигнет турбулентного режима

обтекания. Но она может быть достигнута уже при появле-

нии пограничного слоя или даже вязкого сопротивления.

К тому же, интенсивное охлаждение расплава может не

позволить включению достигнуть максимальной скорости

всплытия. Поэтому расчет максимальной скорости всплы-

тия НМВ не может быть показателем эффективности их

удаления, которую необходимо определять не только по

этой максимально возможной скорости, но и по времени

достижения этой скорости, то есть по ускорению, с кото-

рым НМВ всплывает.

Таким образом, обе формулы из работы [1] не имеют

не только практического подтверждения, но и теоретичес-

кого обоснования, как и утверждение авторов о том, что

при ЦЛ скорость всплытия НМВ в √К раз больше, чем при

обычном литье.

Траектория всплытия НМВ. Рассматривая условия,

при к

оторых во вращаемом жидком металле всплывают

НМВ, авторы монографии совершают две ошибки. Они

утверждают, что при ЦЛ устанавливается «состояние отно-

сительного покоя» жидкого металла. О несостоятельности

этого утверждения говорится в работе [5]. Кольцевой по-

ток расплава во вращаемой форме – это неустановивше-

еся движение. Авторы монографии утверждают, что «при

вращении вокруг горизонтальной оси частицы всплывают

на свободную поверхность радиально по кратчайшему

пути» и представляют это, как «одно из преимуществ цен-

тробежного литья», что противоречит закону сохранения

количества движения, согласно которому mv = const, где

m – масса системы, v – скорость ее движения.

НМВ, переходя, за счет всплытия в сторону свободной

поверхности, на меньший радиус вращения, стремится

увеличить свою угловую скорость вращения. Если вклю-

чение массой m вращается в расплаве со скоростью ω

находясь на радиусе r

, то при переходе на меньший ра-

диус r

оно приобретает скорость ω

, и мы имеем: mω

= mω

, в соответствии с чем скорость вращения НМВ,

к которой оно стремится: ω

= ω

, то есть будет уве-

личиваться и заставлять включение двигаться в танген-

циальном направлении, и это движение усиливается

скольжением слоев жидкого металла. Если НМВ стремит-

ся к увеличению скорости вращения, то расплав, наобо-

рот, из-за скольжения ее уменьшает, создавая активное

кольцевое движение включения относительно расплава.

Таким образом, на всплывающее включение действует не

только выталкивающая сила F

, но и сила F

, действующая

в тангенциальном направлении , и всплытие НМВ при ЦЛ

происходит не радиально по кратчайшему пути, а по бо-

лее сложной траектории. Именно этим объясняется ха-

рактерная только для структуры ЦЛ-металла вытянутая,

ориентированная по окружности форма их скоплений.

Влияние на всплытие включений их формы.

Авторы монографии исключили из рассмотрения этот

фактор. При рассмотрении всплытия шаровидных тел со-

противление жидкости противоположно выталкивающей

силе. В общем случае для тела любой формы направле-

ние силы сопротивления жидкости зависит от формы тела

и представляет собой результирующую сил – лобового со-

противления в направлении движения жидкости и подъ-

емной, действующей в перпендикулярном направлении,

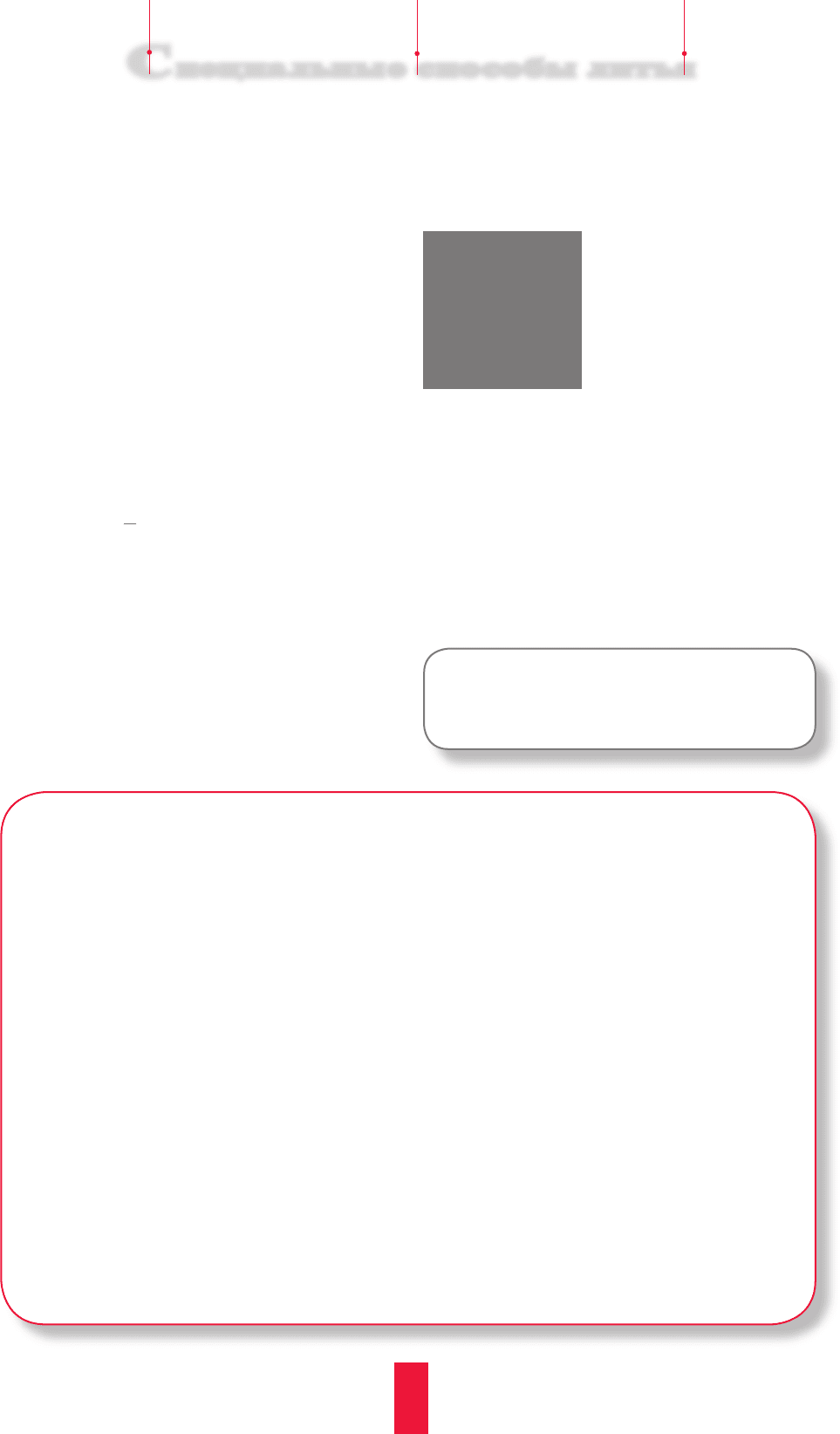
которую еще называют силой Жуковского. Анализ эпюры

сил (рисунок), действующих на включение в расплаве,

показывает, что его всплытию противодействуют силы F

свл

и F

стф

. Силы же F

, F

стл

и F

свф

, действуя в тангенциальном

направлении, этому не противодействуют. Если рассмат-

Эпюра сил,

действующих

на НМВ в жид-

ком металле

при ЦЛ

ЛИТЕЙНОЕ ПРОИЗВОДСТВО№1/2011

пециальные способы литья

Ê àâòîðàì!

К статьям, присылаемым в редакцию,

предъявляются следующие требования:

• статьи должны быть с рецензиями, а также к ним следует добавлять ключевые слова;

• к статье обязательно прилагайте краткую аннотацию на русском и, желательно, английском языках;

•

текст сохраняйте в редакторе MS Word;

• статья должна содержать ссылки на все рисунки и таблицы, а также подписи к ним;

• все рисунки, графики и чертежи должны быть четкими (с разрешением, как минимум, 300 dpi/inch)

и присланы отдельными файлами со стандартными графическими расширениями *.cdr, *.al, *.eps, *.jpeg, *.tif;

• формулы и буквенные обозначения набирайте четко, крупно;

• в тексте ссылка на литературу дается порядковым номером в квадратных скобках, список литературы состав-

ляется в порядке цитирования работ, для статей обязательно указывать название журнала, сборника и т.п., в

которых они опубликованы, год издания, том, начальную страницу;

• объем статьи – не более 8 страниц, рисунков – не более 4;

• статья должна быть подписана всеми авторами.

Также прилагайте подробные сведения об авторах и контактную информацию (адрес, телефон, факс, e-mail)

ривать движение НМВ только в сторону всплытия, уравне-

ние такого движения будет иметь вид:

– F

свл

– F

стф

= 0 (5)

свл

– это сила сопротивления F

, противодействующая

силе всплытия, F

стф

возникает за счет тангенциального

движения включения. По сравнению с уравнением (1), в

уравнении (5) появилась еще одна составляющая – F

стф

Формулы из работы [1] ее не учитывают. Это еще один

довод их несостоятельности.

Не вдаваясь в сложное математическое определение

стф

, важно знать, что она пропорциональна квадрату ско-

рости движения включения в жидком металле в тангенци-

альном направлении.

Выводы

• Известные в теории ЦЛ формулы для расчета ско-

рости всплытия включений и утверждение об увеличении

этой скорости в √К раз, по сравнению со скоростью при

обычном литье, не имеют ни теоретического, ни практи-

ческого обоснования, и их надо признать несостоятель-

ными.

• Действие центробежных сил при ЦЛ, благоприятс-

твуя всплытию НМВ, не гарантирует их более эффектив-

ное удаление из жидкого металла, по сравнению с други-

ми видами литья.

• НМВ всплывают по сложной траектории, имеющей

как радиальную, так и тангенциальную составляющие.

• Возникающая при этом тангенциальная сила и

скольжение жидкого металла – факторы, которые проти-

водействуют всплытию НМВ.

Сведения об авторе

Иванько Е.К.– к

анд. техн. наук.

E-mail: evgenij-ivanko@yandex.ru

1. Юдин С.Б., Левин М.М.,

Розенфельд С.Е. Центробеж-

ное литье. – М.: Машиностро-

ение, 1972.

2. Мирзоян Г.С., Павпе-

рова И.В., Иванько Е.К. Рас-

пределение неметаллических

включений в центробежноли-

СПИСОК

ЛИТЕРАТУРЫ

тых заготовках // Металловедение и термическая обработ-

ка металлов. – 1988. – №2.

3. Яворский Б.М., Детлаф А.А. Справочник по фи-

зике. – М.: Изд-во «Наука», 1979.

4. Ефимов В.А. Разливка и кристаллизация стали.

– М.: Металлургия, 1976.

5. Иванько Е.К. К вопросу об основах центробежного

способа литья // Литейное производство. – 2010. –№2 – С

37–40.

Николай Иванович Бех

К 65-летию со дня рождения

2 января 2011 исполнилось 65 лет Николаю Ивановичу Беху, председателю Редакционных советов журналов «Литейное

производство» и «Металлургия машиностроения», президенту ОАО «Звезда Энергетика», доктору технических наук, доктору

транспорта, профессору, академику инженерной академии и транспорта РФ, академику международных академий – инженерной

и бизнеса, инженерной академии Украины.

Николай Иванович Бех награжден орденами: «За заслуги перед отечеством» III степени, Трудового Красного Знамени, Дружбы

Народов, Знак Почета, а также премией Правительства в области науки и техники и золотым почетным знаком «Общественное

признание».

В 1992 г. Международный географический центр (Кембридж) присвоил Н.И, Беху звание «Человек ХХ века».

После окончания Киевского политехнического института Николай Иванович с 1969 по 1980 г. работал на АвтоВАЗе – инженером-

технологом, начальником бюро, начальником отдела, главным инженером металлургического производства. С 1980 по 1984 гг.

он – директор литейного завода КамАЗа. Это были не лучшие времена для литейного завода, производство подводили литые

детали из ковкого чугуна. Новый директор литейного завода нашел решение – за три с лишним года >100 тыс. т отливок были

переведены на высокопрочный чугун. Личный научный результат – кандидатская а затем и докторская диссертации. А КамАЗ стал

в нашей стране пионером в освоении высокопрочного чугуна. В 1984 г. Н.И. Бех назначается генеральным директором Камского

тракторного завода (г. Елабуга), с 1987 по 1997г. он – генеральный директор КамАЗа. С 1997 по 2001 г. Н.И. Бех – Советник мэра

и правительства Москвы по промышленной политике, генеральный директор Московской управляющей финансовой компании. С

2001 по 2002 г. – старший вице-президент АК «Сибур». В 2003 г. он становится генеральным директором, а с 2005 г. президентом

ОАО «Звезда-Энергетика», компании, которая специализируется на производстве электрогенераторов.

Николай Иванович Бех активно занимался общественной работой: был народным депутатом СССР, депутатом Верховного

Совета Татарской АССР, заместителем председателя Совета по промышленной политике при правительстве СССР. С 1990 по

1991 г. – он член Президентского Совета СССР и попечительского совета независимой организации «Гражданское общество»,

вице-президент Российского Союза Промышленников и Предпринимателей (работодателей) – РСПП.

По единодушному мнению коллег, Николай Иванович – яркий лидер, способный увлечь и повести за собой людей.

Где нужно было сделать невозможное, туда направляли Николая Ивановича. Так было в Елабуге, так было и на КамАЗе. Все

поставленные задачи Николай Иванович решал с честью и высокопрофессионально.

Возглавляемая с 2003 г. Н.И. Бехом компания ОАО «Звезда Энергетика» интенсивно развивается. Менее чем за три года она

заняла лидирующие позиции на рынке малой энергетики России, а в 2004 г. стала победителем всероссийского конкурса «Лучшие

российские предприятия» в номинации «За динамичное развитие» и была сертифицирована по международным стандартам

менеджмента качества ИСО 9001:2000.

Все эти трудные годы Николай Иванович активно поддерживал журнал «Литейное производство», а затем и наши новые

журналы – «Металлургия машиностроения» и «Библиотечка литейщика».

Отмечая юбилей бессменного руководителя Редакционных советов журналов «Литейное производство» и «Металлургия

машиностроения», желаем Николаю Ивановичу Беху здоровья, творческих успехов и процветания наших изданий.

К 75-летию со дня рождения

Аркадий Константинович Тихонов, д-р техн. наук, проф.,

Заслуженный инженер России, Заслуженный изобретатель

СССР, советник по науке ОАО «АВТОВАЗ», родился 13 января

1936 г. В 1960 г. после окончания Магнитогорского горноме-

таллургического института он был направлен на УралАЗ, где

прошел путь от помощника мастера до начальника проектно-

технологического отдела металлургического производства. С

1968 г. А.К. Тихонов работает на ОАО «АВТОВАЗ» – замести-

Аркадий Константинович

Тихонов

телем начальника, начальником термического цеха, начальником управления лабораторно-исследовательских

работ, советником по науке.

Аркадий Константинович участвовал в проектировании цехов серого и ковкого чугуна УралАЗа, возглавлял про-

ектирование и запуск самых крупных и передовых термических цехов АвтоВАЗа, УралАЗа, КамАЗа. Он – постоянный

руководитель «Межотраслевых программ работ по освоению новых видов и улучшению качества металлических,

химических и нефтехимических материалов для автомобилестроения», позволивших освоить в стране основную

номенклатуру материалов, идущих на изготовление автомобилей с европейским уровнем качества.

А.К. Тихонов – известный специалист в области металловедения и термообработки металлов. Им сформули-

рованы научные направления, основанные на применении оксидирования перед низкотемпературным и высоко-

температурным насыщением металлов углеродом и азотом, разработана теория ускорения диффузии оксидом

железа при совместном насыщении углеродом и азотом стали, признанная мировой наукой как «Механизм Тихо-

нова-Криштала». Он, по праву, признан первопроходцем освоения в массовом производстве кратковременного

низкотемпературного газового азотирования. При его участии разработано более 50 марок сталей и чугунов,

совместно с КЭКТИавтопром созданы проходные агрегаты для цементации и отжига, разработаны новые перс-

пективные технологии.

Работы А.К. Тихонов нашли широкое признание в нашей стране и за рубежом. Он – автор более 200 публикаций,

25 патентов, пяти монографий, «Атласов микроструктур сталей». Он – почетный прокатчик России, действительный

член Российской и Международной инженерных академий, научный руководитель АНТЦ «Материаловедение и

технология» поволжского отделения РИА, председатель Самарского отделения ассоциации металловедов России,

ASM International (Чикаго), Итальянской ассоциации металлургов (Милан), Международного общества металло-

ведов (Женева), член Высшего инженерного совета России. Аркадий Константинович активно передает научный

и производственный опыт сотрудникам, студентам и аспирантам, под его руководством защищены кандидатские

и докторские диссертаций. Он – член редколлегии ряда журналов, в том числе «Металлургия машиностроения»

и «Литейное производство», организатор всесоюзных конференций по термообработке, международных кон-

ференций «Материалы в автомобилестроении», участник международных конгрессов по металлам и литейному

производству. Он – лауреат премии им. П.П. Аносова, за разработку и освоение новых сталей и технологии их

обработки, награжден медалями ВДНХ, золотыми медалями Международной и Российской инженерных академий,

золотой медалью им. Б.Е. Патона НАН Украины, имеет ордена «Трудового красного знамени», «Знак почета»,

медаль за трудовую доблесть в честь 100-летия В.И. Ленина.

Сердечно поздравляем Аркадия Константиновича с юбилеем и желаем ему здоровья и творческого долголе-

тия.

Россия, 119331, Москва, Проспект Вернадского 29,

Тел.: (495) 787-28-71, факс: (495) 787-28-72

www.ognecom.ru foundry@ognecom.ru

Эксклюзивный поставщик продукции

в России ООО "РЕДАГ"

Футеровочные материалы для индукционных печей и канальных миксеров

Сплавы Zn, Al, Cu, Ni, Fe

Футеровка печей материалами SAINT-GOBAIN, торговая марка NORTON

Сопровождение футеровки, спекания, плавки специалистами компании

ПеноКерамические Фильтры для сплавов Al , Cu, Ni, Fe

Расчет литниковых систем

Техническая поддержка применение ПКФ специалистами компании SELEE

40 лет работы на рынке Северной Америки, Европы, Азии

ЛИТЕЙНОЕ ПРОИЗВОДСТВО №1/2011

рганизация производства

Аннотация

The Summary

I. Производственная эффективность

Производство одинакового объема литейной продук-

ции в России занимает на 60% больше времени, чем в

Евросоюзе в связи с низкой производственной эффек-

тивностью.

Показатель производственная эффективность про-

слеживает выполнение производственного плана во

времени и показывает фактический расход времени для

Автор статьи – руководитель проекта «Повышение ресурсоэф-

фективности машиностроения и литейного производства в России»

IFC, (Международная финансовая корпорация, член группы Всемир-

ного Банка)

К.К. Турилова

Kristina Turilova

International Fi-

nance Corporation,

World Bank Group

Сравнение российских и

европейских литейных

предприятий по ключевому

показателю производственная

эффективность

Comparison of Russian and

European foundries against the key

performance indicators total effec-

tive equipment productivity and

capacity utilization

Статья продолжает цикл публикаций, посвященных результатам всесторонне-

го практического исследования потенциала ресурсоэффективности литейной

отрасли России. Автор отвечает на вопрос о том, как предприятия могут по-

высить свою производственную эффективность по двум из семи к лючевых

показателей эффективности (КПЭ) литейного производства –

про-

изводственная эффективность

общая эффективная производительность обо-

рудования

. В последующих статьях будут представлены результаты анализа

оставшихся четырех показателей эффективности: расходу – энергии, свежего

песка, свежей воды; производительности труда.

This article continues the series of publications on the results of the recent resource

efficiency benchmarking study of Russian ferrous foundry industry. The author high-

lights how foundries can improve their operational performance by looking specifically

at two of seven key performance indicators (KPIs) – total effective equipment pro-

ductivity and capacity utilization. Next articles in this series will present benchmarking

results and recommendations for further improvements in another four KPIs: energy

consumption, sand consumption, fresh water consumption, labor productivity.

производства годных отливок, в % от запланированного

времени.

КПЭ состоит из четырех п о к а з а т е лей, %:

• простой;

• задержки;

• бракованные формы;

• бракованные отливки.

Этот КПЭ влияет на повышение производительности

как труда, так и оборудования.

Фактор производительности – (расход времени к ко-

личеству годных отливок – РФ против ЕС).

• Лучшая практика (ЛП) – 1,07.

• Средняя практика (СП) – 0,63