Li S.Z., Jain A.K. (eds.) Encyclopedia of Biometrics

Подождите немного. Документ загружается.

federal legal proceedings (the citation is Daubert v.

Merrell Dow Pharmaceuticals, 509 U.S. 579).

▶ Gait, Forensic Evidence of

Daugman Algorithm

▶ Iris Encoding and Recognition using Gabo r

Wavelets

Dead Finger Detection

▶ Fingerprint Fake Detection

Decision

Decision is the output result of a biometric system

given a biometric sample. For a veriﬁcation task, the

decision is ‘‘reject or accept’’ of the claimed identity,

while for identiﬁcation task it is the identity of the

presented subject or rejecting him or her as one of

the enrolled subject.

▶ Performance Evaluation, Overview

Decision Criterion Adjustment

▶ Score Normalization Rules in Iris Recognition

Deformable Models

THOMAS ALBRECHT,MARCEL LU

THI,THOMAS VETTE R

Computer Science Department, University of Basel,

Switzerland

Synonyms

Statistical Models; PCA (Principal Component Analysis);

Active (Contour, Shape, Appearance) Models; Morph-

able Models

Definition

The term Deformable Model describes a group of

computer algorithms and techniques widely used in

computer vision today. They all share the common

characteristic that they model the variability of a cer-

tain class of objects. In biometrics this could be the

class of all faces, hands, or eyes, etc. Tod ay, different

representations of the object classes are commonly

used. Earlier algorithms modeled shape variations

only. The shape, represented as curve or surface, is

deformed to match a speciﬁc example in the object

class. Later, the representations were extended to

model texture variations in the object classes as well

as imaging factors such as perspective projection and

illumination effects. For biometrics, deformable mod-

els are used for image analysis such as face recognition,

image segmentation, or classiﬁcation. The image anal-

ysis is performe d by ﬁtting the deformable model to a

novel image, thereby parametrizing the novel image in

terms of the known model.

Introduction

Deformable models denote a class of methods that

provide an abstract model of an object class [1]by

modeling separa tely the variability in shape, texture,

or imaging conditions of the objects in the class. In its

most basic form, deformable models represent the

shape of objects as a ﬂexible 2D cur ve or a 3D surface

that can be deformed to match a particular instance of

that object class. The deformation a model can under-

go is not arbtitrary, but should satisfy some problem-

speciﬁc constraints. These constraints reﬂect the prior

210

Daugman Algorithm

knowledge about the object class to be modeled.

The key considerations are the way curves or surfaces

are represented and the different form of prior knowl-

edge to be incorporated. The different ways of repre-

senting the curves range from parametrized curves in

2D images, as in the ﬁrst successful method introduced

as Snakes in 1988 [2], to 3D surface meshes in one of

the most sophisticated approaches, the 3D Morphable

Model (3DMM) [3], introduced in 1999. In the case

of Snakes, the requirement on the deformation is that

the ﬁnal deformed curve should be sm ooth. In the

3DMM, statistical information about the object class

(e.g., such as the class of all faces) is used as prior

knowledge. In other words, the constraint states that

the deformed surface should with high probability

belong to a valid instance of the object class that is

modeled. The required probability distributions are

usually derived from a set of representative examples

of the class.

All algorithms for matching a deformation model

to a given data set are deﬁned as an energy minimiza-

tion problem. Some measure of how well the deformed

model matches the data has to be minimized. We call

this the external energy that pushes the model to match

the data set as good as possible. At the same time the

internal energy, representing the prior knowledge,

has to be kept as low as possible. The internal energy

models the object’s resistance to be pushed by the

external force into directions not coherent with the

prior knowledge. The optimal solution constitutes

an equilibrium of internal and external forces. For

instance, in the case of Snakes, this means that a

contour is pushed to an image feature by the external

force while the contour itself exhibits resistance to be

deformed into a non-smooth curve. In the case of

the 3DMM, the internal forces become strong when

the object is deformed such that it does not belong

to the modeled object class.

This concept can be expressed in a formal frame-

work. In each of the algorithms, a model M has to be

deformed in order to best match a data set D. The

optimally matched model M



is sought as the mini-

mum of the energy functional E, which is comprised of

the external and internal energies E

ext

and E

int

E½M ¼ E

ext

½M; D þ E

int

½M ð1Þ



¼ arg min

E½M: ð2Þ

Snakes

Kaas et al. introduced Snakes, also known as the Active

Contour Model in their landmark paper [2]. Here, the

deformable model M is a parametrized curve and

the goal is to segment objects in an image D by ﬁtting

the curve to object boundaries in the image.

The external energy E

ext

½M; D measures how well the

snake matches the boundaries in the image. It is

expressed in form of a feature image, for instance,

an edge image. If an edge image I with low values on

the edges of the image is used, the external energy is

given as:

ext

½M; D ¼ E

ext

½v; I¼

IðvðsÞÞds; ð3Þ

where v : [0,1] !IR

is a suitable parametrization

of the curve M and I :IR

!IR is the edge image of

the input image D. If a point v ( s) of the curve lies on

a boundary, the value of the edge image I(v(s)) at this

point is low. Therefore, the extern al energy is mini-

mized if the curve comes to lie completely on a bound-

ary of an image.

The internal energy ensures that the curve always

remains a smooth curve. For the classical snakes for-

mulation, it is deﬁned as the spline bending energy of

the curve:

int

½M ¼ E

int

½v¼ðaðsÞjv

ðsÞj

þ bðsÞjv

ðsÞj

Þ=2;

ð4Þ

where a and b control the weight of the ﬁrst and

second derivative terms.

By ﬁnding a minimum of the combined functio nal

E½M, the aim is to ﬁnd a smooth curve M, which

matches the edges of the image and thereby segments

the objects present in the image.

The Snake methodolog y is the foundation for

a large number of methods based on the same

framework. There are three main lines of

development:



Flexible representation of curves and surfaces



Incorporation of problem speciﬁc prior know-

ledge from examples of the same object class



Use of texture to complement the shape

information

Deformable Models

211

Level Set Representation for Curves

and Surfaces

The idea of snakes was to represent the curve M as a

parametric curve. While such a representation is simple,

it is topologically rigid, i.e., it cannot represent objects

that are comprised of a variable number of independent

parts. Caselles et al. [4] proposed to represent the curve

M as a level set, i.e., the contour is represented as the

zero level set of an auxiliary function f:

M¼ff ¼ 0g: ð5Þ

A typical choice for f is the distance function to the

model M.

This representation offers more topological ﬂexi-

bility, because contours represented by level sets can

break apart or join without the need of reparametri-

zation. Additionally, the level set formulation allows

a treatment of surfaces and images in any dimension,

without the need of reformulating the methods or algo-

rithms. The idea of representing a surface by a level-set

has led to a powerful framework for image segmenta-

tion, which is referred to as level-set segmentation.

Example Based Shape Priors

Before the introduction of Active Shape Models [5],

the internal energy or prior knowledge of the Deform-

able Model has been very generic. Independent of the

object class under consideration, the only prior knowl-

edge imposed was a smoothnes s constraint on the

deformed model. Active Shape Models or ‘‘Smart

Snakes’’ and the 3DMM [3] incorporate more speciﬁc

prior knowledge about the object class by learning the

typical shapes of the class.

The main idea of these methods is to assume that

all shapes in the object class are distributed according

to a multivariate normal distribution. Let a representa-

tive training set of shapes M

; ...; M

, all belonging

to the same object class be given. Each shape M

represented by a vector x

containing the coordinates of

a set of points. For 2D points (x

, y

), such a vector x

takes the form x ¼ðx

; y

; ...; x

; y

Þ: For the result-

ing example vectors x

,...,x

, we can estimate the

mean

x and covariance matrix S. Thus, the shapes

are assumed to be distributed according to the multi-

variate normal distribution Nð

x; SÞ. To conveniently

handle this normal distribution, its main modes of

variation, which are the eigenvectors of S, are cal-

culated via

▶ Principal Components Analysis (PCA)

[6]. The corresponding eigenvalues measure the ob-

served variance in the direction of an eigenvector.

Only the ﬁrst k most signiﬁcant eigenvectors v

,...,v

corresponding to the largest eigenvalues are used, and

each shape is modeled as:

x ¼

x þ

i¼1

; ð6Þ

with a

2IR. In this way, the prior knowledge about the

object class, represented by the estimated normal dis-

tribution Nð

x; SÞ, is used to deﬁne the internal energy.

Indeed, looking at Equation (6), we see that the shape

can only be deformed by the principal modes of varia-

tion of the training examples.

Furthermore, the coefﬁcients a

are usually con-

strained, such that deformations in the direction of v

are not much larger than those observed in the training

data. For the Active Shape Model, this is achieved by

introducing a threshold D

max

on the mean squares of

the coefﬁcients a

, scaled by the corresponding stan-

dard deviation s

of the training data. The internal

force of the Active Shape Model is given by :

int

½M ¼ E

int

½a

; ...; a



0if

i¼1

 D

max

1 else:

(

ð7Þ

In contrast, the 3DMM [3] does not strictly constrain

the size of these coefﬁcients. Rather, the assumed mul-

tivariate normal distributions Nð

x; SÞ is used to

model the internal energy of a deformed model M as

the probability of obser ving this model in the normally

distributed object class:

int

½M ¼ E

int

½a¼ln PðaÞ

¼ln e



i¼1

ða

i¼1

ða

ð8Þ

Correspondence and Registration

All deformable models using prior knowledge in form

of statistical information presented here assume the

212

Deformable Models

example data sets to be in correspondence. All objects

are labeled by the same number of points and

cor responding points always label the same part of

the object. For instance in a shape model of a han d, a

given point could always label the tip of the index

ﬁnger in all the examples. Without this correspon-

dence assumption, the resulting statistics would not

capture the variability of features of the object but

only the deviations of the coordinates of the sampled

points. The task of bringing a set of examples of the

same object class into correspondence is known as the

Registration Problem and constitutes another large

group of algorithms in computer vision.

Incorporating Texture Information

One limitation of the classical Snake model is that the

information of the data set D is only evaluated at

contour points of the model M. In level-set

▶ segmen-

tation, new external energy terms have been intro-

duced in [7, 8]. Instead of measuring the goodness of

ﬁt only by the values of the curve M on a feature

image, in these new approaches the distance between

the original image and an approximation deﬁned by

the segmentation is calculated. Typical approximations

are images with constant or smoothly varying values

on the segments. This amounts to incorporating the

prior knowledge that the appearance or texture of the

shape outlined by the deformable model is constant or

smooth.

By incorporating more speciﬁc prior knowledge

about the object class under consideration, the appear-

ance or texture can be modeled much more precisely.

This can be done in a similar fashion to the shape

modeling described in the previous section. The ap-

pearance or texture T of a model M is represented by

a vector T. All such vectors belonging to a speciﬁc

object class are assumed to be normally distributed.

For instance, it is assumed that the texture images of all

faces can be modeled by a multivariate normal distri-

bution. Similar to the shapes, these texture vectors

need to be in correspondence in order to permit a

meaningful statistical analysis.

Given m example textures T

,...,T

, which are in

correspondence, their mean

T, covariance matrix S

main modes of variation t

,...,t

, and eigenvalues r

can be calculated. Thus, the multivariate normal

distribution Nð

T; S

Þ can be used to model all tex-

tures of the object class, which are then represented as:

T ¼

T þ

i¼1

: ð9Þ

A constraint on the coefﬁcients b

analogous to Equa-

tion (7)or(8) is used to ensure that the model texture

stays in the range of the example textures. In this

way, not only the outline or shape of an object from

the object class but also its appearance or texture can

be modeled. The Active Appearance Models [1, 9, 10]

and the 3D Morphable Model [3 ] both use a combined

model of shape and texture to model a speciﬁc object

class. A complete object is modeled as a shape given

by Equation (6) with texture given by Equation (9).

The model’s shape and texture are deformed by choos-

ing the shape and texture coefﬁcients a¼(a

,...,a

)

and b¼(b

,...,b

). The external energy of the model is

deﬁned by the distance between the input data set D

and the modeled objec t ( S,T), measured with a dis-

tance measure which not only takes the difference in

shape but also that in texture into account. The inter-

nal energy is given by Equation (7)or(8) and the

analogous equation for the b

2D versus 3D Representation

While the mathematical formalism describing all pre-

viously introduced models is independent of the di-

mensionality of the data, historically the Active

Contour, Shape, and Appearance Models were only

used on 2D images, whereas the 3DMM was the ﬁrst

model to model an object class in 3D. The main differ-

ence between 2D and 3D modeling is in the expressive

power and the difﬁculty of building the deformable

models. Deformable models, when incorporating prior

knowledge on the objects class, are derived from a set

of examples of this class. In the 2D case these examples

are usually registered images showing different

instances of the class. Similarly, 3D models require

registered 3D examples. As an additional difﬁculty,

3D examples can only be obtained with a complex

scanning technology, e.g., CT, MRI, laser, or structured

light scanners. Additionally, when applied to images

the 3D models require a detailed model for the imag-

ing process such as the simulation of occlusions, per-

spective, or the effects of variable illumination.

Deformable Models

213

While building 3D models might be difﬁcult, 3D

models naturally offer a better separation of object

speciﬁc parameters from parameters such as pose and

illumination that orig inate in the speciﬁc imaging

parameters. For 2D mode ls these parameters are often

extremely difﬁcult to separate. For instance, with a 2D

model, 3D pose changes can only be modeled by shape

parameters. Similarly, 3D illumination effects are mod-

eled by texture variations.

Applications

Deformable Models have found a wide range of appli-

cations in many ﬁelds of computer science. For

biometrics, the most obvious and well-researched

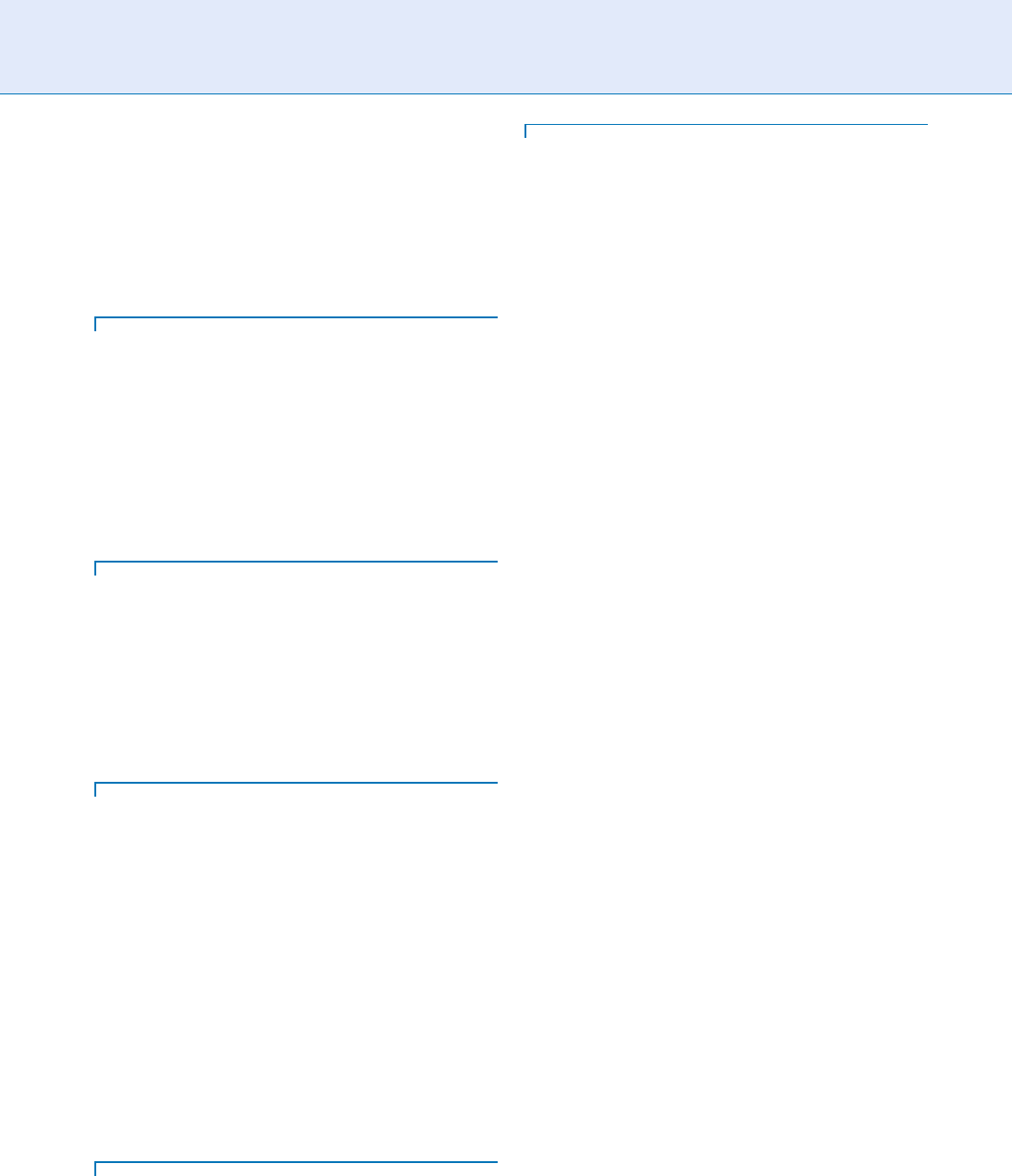
applications are certainly face tracking ([10], Fig. 1)

and face recognition, [11]. For face recognition, the

fact is exploited that an individual face is represented

by its shape and texture coefﬁcients. Faces can be

compared for recognition or veriﬁcation by comparing

these coefﬁcients.

Another important area in which Deformable

Models have found application is in medical image

analysis, most importantly medical image segmenta-

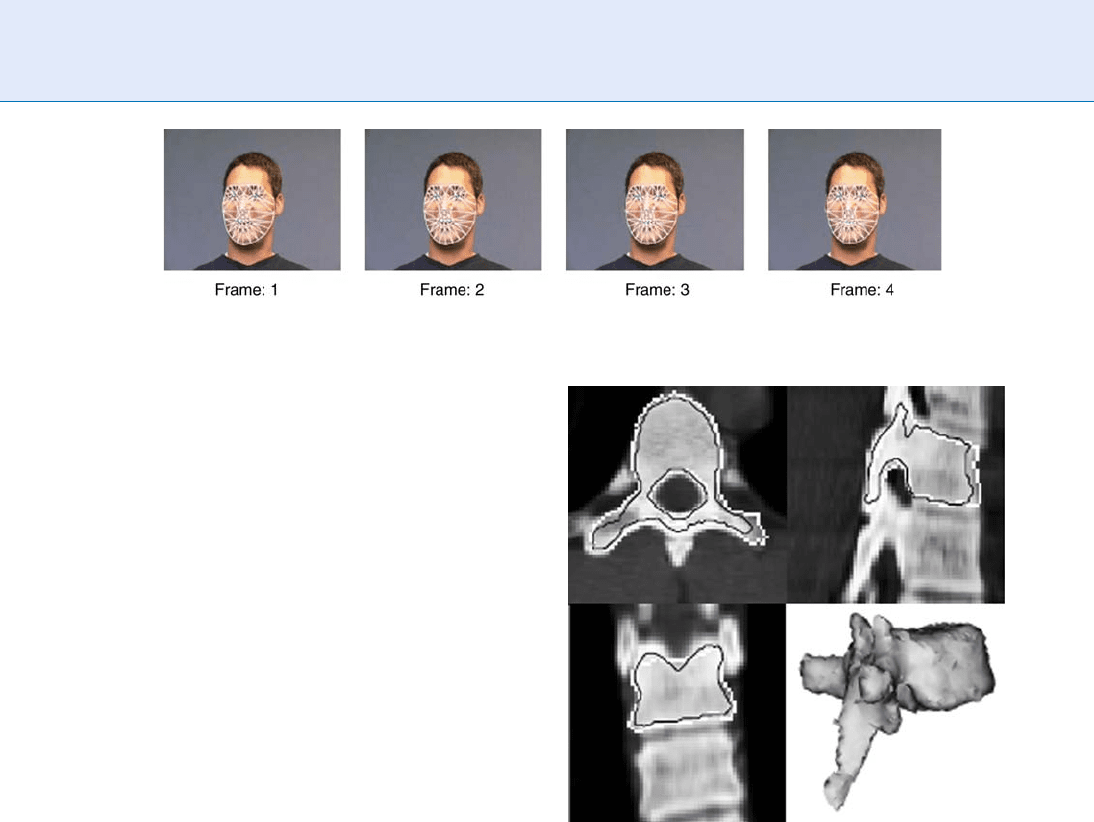
tion, ([12], Fig. 2).

Recent Developments

While the level-set methods allow for greater topologi-

cal ﬂexibility, the Active Appearance Model and

the 3DMM in turn provide an internal energy term

representing prior knowledge about the object class.

It is natural to combine the advantages of all these

methods by using the level-set representation and its

resulting external energy term together with the inter-

nal energy term incorporating statistical prior knowl-

edge. In [12], Leventon et al. propose such a method

that relies on the level-set representation of snakes

introduced by Caselles et al. [4]. The internal energy

is given by statistical prior knowledge computed di-

rectly from a set of level-set functions (distance func-

tions) representing the curves using a standard PCA

approach.

Summary

Deformable models provide a versatile and ﬂexible

framework for representing a certain class of objects

by specifying a model of the object together with

its variations. The variations are obtained by deform-

ing the model in accordance to problem speciﬁc

constraints the deformation has to fulﬁll. These

Deformable Models. Figure 1 Tracking a face with the active appearance model. Image from [10].

Deformable Models. Figure 2 3D level set segmentation

with shape prior of a vertebrae. Image from [12].

(ß 2000 IEEE).

214

Deformable Models

constraints represent the prior knowledge about the

object and can range from simple smoothness assump-

tion on the deformed object to the requirement

that the resulting object still belongs to the same object

class. The analysis of novel objects is done by ﬁtting

the deformable model to characteristics of a new

object. The ﬁtting ranges from simple approaches of

matching the object’s boundar y in an image, to opti-

mally matching the object’s full texture. Because of

their ﬂexibility, deformable models are used for many

applications in biometrics and the related ﬁelds of

computer vision and medical image analysis. Among

others, the most successful use of these models are

in automatic segmentation and image analysis and

synthesis [3].

Related Entries

▶ Active (Contour, Shape, Appearance) Models

▶ Face Alignment

▶ Face Recognition, Over view

▶ Image Pattern Recognition

References

1. Vetter, T., Poggio, T.: Linear object classes and image synthesis

from a single example image. IEEE Trans. Pattern Anal. Mach.

Intell. 19(7), 733–742 (1997)

2. Kass, M., Witkin, A., Terzopoulos, D.: Snakes: Active contour

models. Int. J. Comput. Vis. 1(4), 321–331 (1988)

3. Blanz, V., Vetter, T.: A morphable model for the synthesis of 3d

faces. In: SIGGRAPH ’99: Proceedings of the 26th annual con-

ference on Computer graphics and interactive techniques, pp.

187–194. ACM Press (1999). DOI http://doi.acm.org/10.1145/

311535.311556

4. Caselles, V., Kimmel, R., Sapiro, G.: Geodesic Active Contours.

Int. J. Comput. Vis. 22(1), 61–79 (1997)

5. Cootes, T., Taylor, C.: Active shape models-’smart snakes’. In:

Proceedings British Machine Vision Conference, pp. 266–275

(1992)

6. Bishop, C.: Pattern recognition and machine learning. Springer

(2006)

7. Chan, T.F., Vese, L.A.: Active contours without edges. IEEE

Trans. Image Process. 10(2), 266–277 (2001)

8. Mumford, D., Shah, J., for Intelligent Control Systems (US, C.:

Optimal Approximations by Piecewise Smooth Functions and

Associated Variational Problems. Center for Intelligent Control

Systems (1988)

9. Cootes, T., Edwards, G., Taylor, C.: Active appearance models.

IEEE Trans. Pattern Anal. Mach. Intell. 23(6), 681–685 (2001)

10. Matthews, I., Baker, S.: Active Appearance Models Revisited. Int.

J. Comput. Vis. 60(2), 135–164 (2004)

11. Blanz, V., Vetter, T.: Face recognition based on ﬁtting a 3 D

morphable model. IEEE Trans. Pattern Anal. Mach. Intell.

25(9), 1063–1074 (2003)

12. Leventon, M.E., Grimson, W.E.L., Faugeras, O.: Statistical shape

inﬂuence in geodesic active contours. IEEE Comput. Soc. Conf.

Comput. Vis. Pattern Recogn. 1, 1316 (2000). DOI http://doi.

ieeecomputersociety.org/10.1109/CVPR.2000.855835

Deformation

Since expressions are common in faces, robust face

tracking methods should be able to perform well

inspite of large facial expressions. Also, many face

trackers are able to estimate the expression.

▶ Face Tracking

Delta

The point on a ridge at or nearest to the point of

divergence of two type lines, and located at or directly

in front of the point of divergence.

▶ Fingerprint Templates

Demisyllables

A demisyllable brackets exactly one syllable-to-syllable

transition. Demisyllable boundaries are positioned

during the stationary portion of the vowel where

there is minimal coarticulation. For general American

English, a minimum of 2,500 demisyllables are

necessary.

▶ Voice Sample Synthesis

Demisyllables

215

Dental Biometrics

HONG CHEN,ANIL K. JAIN

Michigan State University, East Lansing, MI, USA

Synonyms

Dental identiﬁcation; Forensic Identiﬁcation Based on

Dental Radiographs; Tooth Biometrics

Definition

Dental biometrics uses information about dental

structures to automatically identify human remains.

The methodology is mainly applied to the identiﬁ-

cation of victims of massive disasters. The process of

dental identiﬁcation consists in measuring dental fea-

tures, labeling individual teeth with tooth indices, and

the matching of dental features. Dental radiographs are

the major source for obtaining dental features. Com-

monly used dental features are based on tooth mor-

phology (shape) and appearance ( gray level).

Motivation

The signiﬁcance of automatic dental identiﬁcation

became evident after recent disasters, such as the 9/11

terrorist attack in the United States in 2001 and the

Asian tsunami in 2004. The victims’ bodies were seriously

damaged and decomposed due to ﬁre, water, and other

environmental factors. As a result, in man y cases, com-

mon biometric traits, e.g., ﬁngerprints and faces, were not

available. Therefore dental features may be the only clue

for identiﬁcation. After the 9/11 attack, about 20% of the

973 victims identiﬁed in the ﬁrst year were identiﬁed

using dental biometrics [1]. About 75% of the 2004

Asian tsunami victims in Thailand were identiﬁed

using dental records [2]. Table 1 gives a comparison

between dental biometrics and other victim identiﬁca-

tion approaches, i.e.,

▶ circumstantial identiﬁcation,

external identiﬁcation, internal identiﬁcation, and

▶ genetic identiﬁcation [3]. The number of victims

to be identiﬁed based on dental biometrics is often

very large in disaster scenarios, but the traditional

manual identiﬁcation based on forensic odontology

is time consuming. For example, the number of Asian

tsunami victims identiﬁed during the ﬁrst 9 months

was only 2,200 (out of an estimated total of 190,000

victims) [2]. The low efﬁciency of manual methods for

dental identiﬁcation makes it imperative to develop auto-

matic methods for matching dental records [4, 5].

Dental Information

Dental information includes the number of teeth, tooth

orientation, and shape of dental restorations, etc.

This information is recorded in dental codes, which

are symbolic strings, describing types and positions of

dental restorations, presence or absence of each tooth,

and number of cusps in teeth, etc. Adams concluded

from his analysis [7] that when adequate antemortem

(AM) dental codes are available for comparison with

postmortem (PM) dental codes, the inherent variability

of the human dentition could accurately establish iden-

tity with a high degree of conﬁdence. Dental codes are

entered by forensic odontologists after carefully

reading dental radiographs. Dental radiographs, also

called dental X-rays, are X-ray images of dentition.

Compared to dental codes, dental radiographs contain

richer information for identiﬁcation, and, therefore,

are the most commonly used source of information

for dental identiﬁcation.

Dental Biometrics. Table 1 A comparison of evidence types used in victim identification [6]

Physical

Identification approach Circumstantial External Internal Dental Genetic

Accuracy Med. High Low High High

Time for identification Short Short Long Short Long

Antemortem record availability High Med. Low Med. High

Robustness to decomposition Med. Low Low High Med.

Instrument requirement Low Med. High Med. High

216

Dental Biometrics

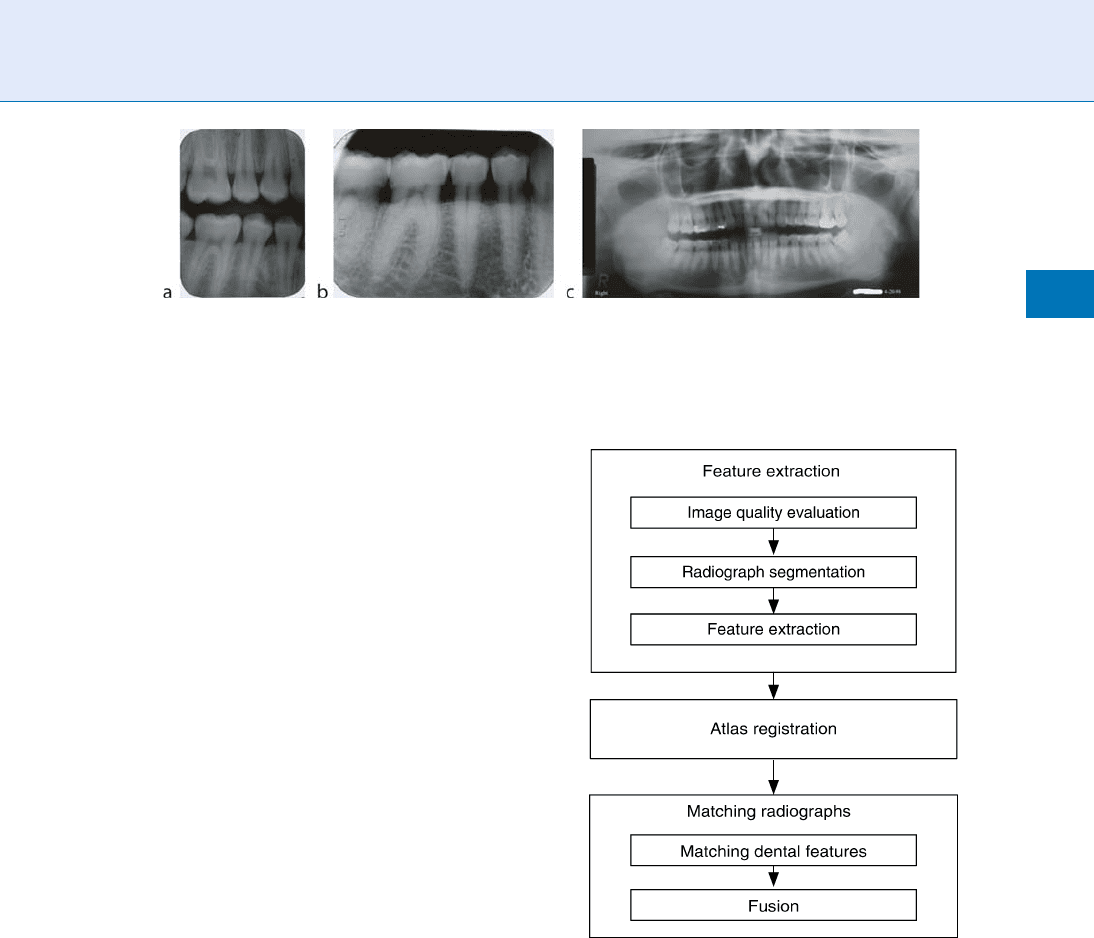
There are three common t ypes of den tal radio-

graphs: periapical, bitewing, and panoramic. Periapical

X-rays (Fig. 1a) show the entire tooth, including

the crown, root, and the bone surrounding the root.

Bitewing X-rays (Fig. 1b) show both upper and lower

rows of teeth. Panoramic X-rays (Fig. 1c) give a broad

overview of the entire dentiti on (the development of

teeth and their arrangement in the mouth), providing

information not only about the teeth, but also about

upper and lower jawbones, sinuses, and other tissues

in head and neck. Digital radiographs will be used for

victim identiﬁcation in future due to their advantages

in speed, storage, and image qualit y.

Antemortem Dental Records

Forensic identiﬁcation of humans based on dental in-

formation requires the availability of antemortem den-

tal records. The discovery and collection of antemortem

records is ordinarily the responsibility of investigative

agencies. Antemortem dental radiographs are usually

available from dental clinics, oral surgeons, orthodon-

tists, hospitals, military service, insurance carriers, and

the FBI National Crime Information Center (NCIC).

Automatic Dental Identification

System

Figure 2 shows the system diagram of an automatic

dental identiﬁcation system [6 ]. The system consists

of three steps: extraction of features, registration of

dentition to a dental atlas, and matching dental fea-

tures. The ﬁrst step involves image quality evaluation,

segmentation of radiographs, and extraction of dental

information from each tooth. The second step labels

teeth in dental radiog raphs so that only the cor-

responding teeth are matched in the matching stage.

Dental features extracted from PM and AM images are

matched in the third step. For many victims that need

to be identiﬁed, several AM and PM dental radiographs

are available. Therefore, there can be more than one

pair of corresponding teeth. In such cases, the matching

step also fuses matching scores for all pairs of cor-

responding teeth to generate an overall matching

score between the AM and PM images. Figure 3

shows the process of matching a pair of AM and PM

dental radiographs.

Dental Biometrics. Figure 1 Three types of dental radiographs. (a) A bitewing radiograph; (b) a periapical radiograph;

Dental Biometrics. Figure 2 Block diagram of automatic

dental identification system.

Dental Biometrics

217

Feature Extraction

The ﬁrst step in processing dental radiographs is to

segment dental radiographs into regions, each contain-

ing only one tooth. Segmentation of dental radiographs

uses Fast Marching algorithm [8] or integral projection

[9, 10]. Figure 4 shows examples of successful radio-

graph segmentation by the Fast Marching algorithm.

Due to the degradation of X-ray ﬁlms over time as well

as image capture in ﬁeld env ironments, AM and PM

radiographs are often of poor quality, leading to seg-

mentation errors. To prevent propagation of errors in

segmentation, an image quality evaluation module is

introduced [6]. If the estimated image quality is poor,

an alert is triggered to get human experts involved dur-

ing segmentation.

Dental features are extracted from each tooth. The

most commonly used features are the contours of teeth

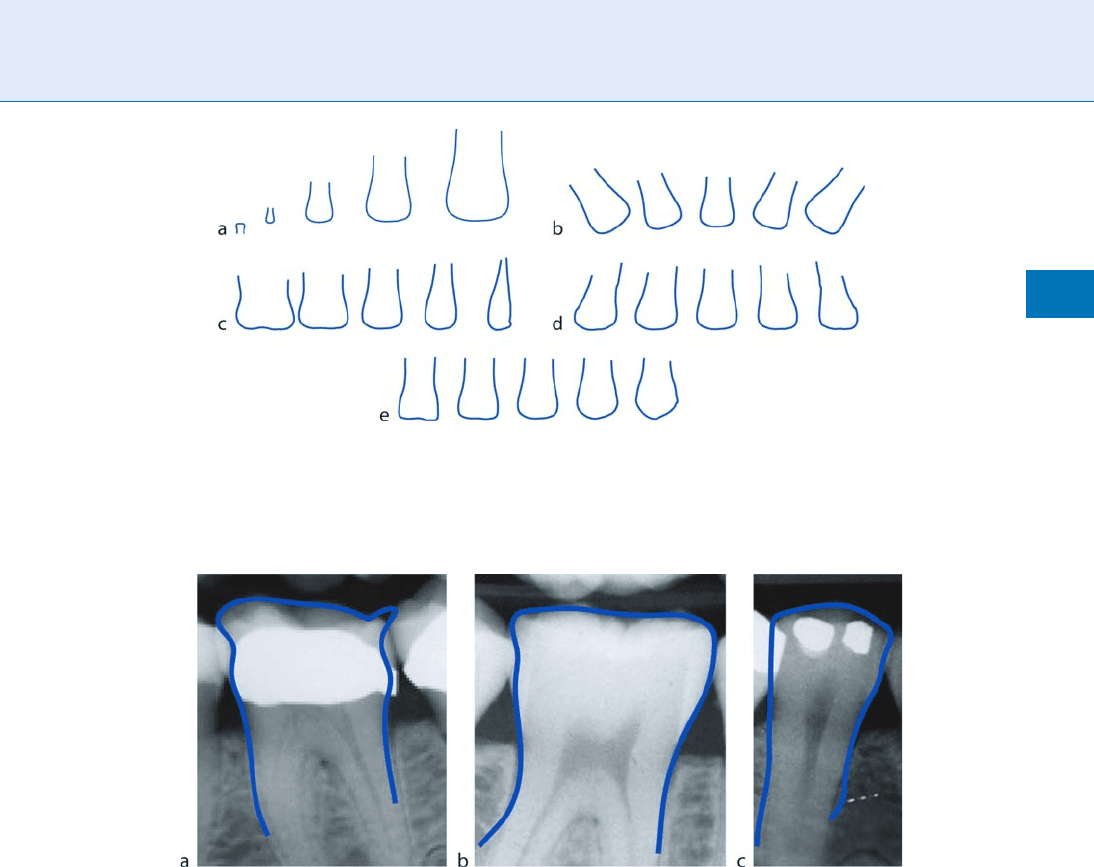
and the contours of dental work. Active shape models

are used to extract eigen-shapes from aligned training

tooth contours [6]. Figure 5 shows the ﬁve most prin-

cipal deformation modes of teeth, which, respectively,

represent scaling, rotation, variations in tooth width,

variations in tooth orientation, and variations in

shapes of tooth root and crown. Figure 6 shows some

extracted contours. Anisotropic diffusion is used to

enhance radiograph images and segment regions of

dental work (including crowns, ﬁllings, and root canal

treatment, etc.) [9]. Thresholding is used to extract the

boundaries of dental work (Fig. 7).

Atlas Registration

The second step is to register individual teeth segmented

in radiographs to a

▶ human dental atlas (Fig. 8). This

allows for labeling the teeth with tooth indices. Nomir

and Abdel-Mottaleb [11] proposed to form a symbolic

string by concatenating classiﬁcation results of the

teeth and match the string against known patterns of

Dental Biometrics. Figure 3 Matching a pair of PM and

AM images.

Dental Biometrics. Figure 4 Some examples of correct segmentation.

218

Dental Biometrics

tooth arrangement to ﬁnd out tooth indices. To hand le

classiﬁcation errors and missing teeth, Chen and Jain

[12] proposed a hybrid model composed of Support

Vector Machines (SVMs) and a Hidden Markov Model

(HMM) (Fig. 9). The HMM serves as an underlying

representation of the dental atlas, with HMM states

representing teeth and distances between neighboring

teeth. The SVMs classify the teeth into three classes

based on their contours. Tooth indices, as well as

Missing teeth, can be detected by registering the ob-

served tooth shapes and the distances between adjacent

teeth to the hybrid model. Furthermore, instead of

simply assigning a class label to each tooth, the hybrid

model assigns a probability of correct detection to

possible indices of each tooth. The tooth indices with

the highest probabilities are used in the matching

stage. Figure 10 shows some examples of tooth index

estimation.

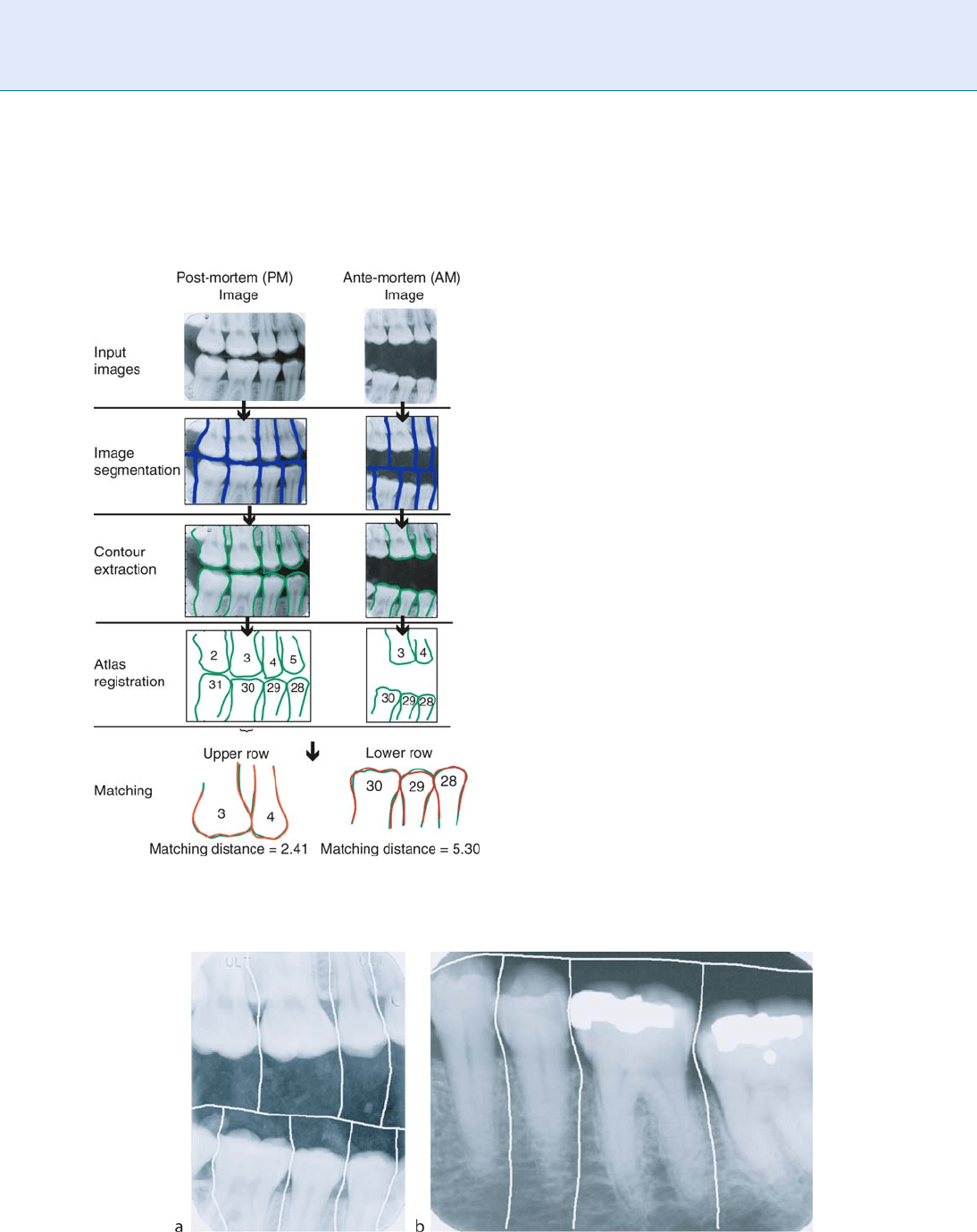
Matching

For matching the corresponding teeth from PM and

AM radiographs, the tooth contours are registered

using scaling and a rigid transformation, and corres-

ponding contour points are located for calculating the

distance between the contours [9]. If dental work is

present in both the teeth, the regions of dental work are

also matched to calculate the distance between dental

work. The matching distance between tooth contours

and between dental work contours are fused to generate

the distance between the tw o teeth [9]. Given the match-

ing distances between individual pairs of teeth, the

matching distance between two dental radiographs is

computed as the average distance of all the corresponding

teethinthem.Thedistancebetweenthequeryanda

record in the database is calculated based on the dis-

tance between all the available dental radiographs in the

Dental Biometrics. Figure 5 First five modes of the shape model of teeth. The middle shape in each image is the mean

shape, while the other four shapes are, from left to right, mean shape plus four eigenvectors multiplied by 2, 1, 1,

and 2 times the square root of the corresponding eigenvalues.

Dental Biometrics. Figure 6 Tooth shapes extracted using Active Shape Models.

Dental Biometrics

219