Леонов Г.А. Лекции по курсу теории управления I (анализ)

Подождите немного. Документ загружается.

Тогда уравнения (2.13) запишем в следующем виде:

˙x

= x

˙x

n−1

= x

˙x

= −N

n−1

− . . . − N

+ ξ(t),

σ = M

m+1

+ M

m−1

+ . . . + M

Поэтому здесь

A =







0 1 0 0 . . . 0

0 0 1 0 . . . 0

0 0 0 1 . . . 0

0 0 0 0 . . . 1

−N

. . . . . . . . . . . . −N

n−1







, b =













c =













, x





(0)









η(0)

(n−1)

(0)





Напомним, что решение уравнения (2.14) может быть записано в следующей интегральной

форме (формула Коши):

x(t) = e

A(t−τ )

bξ(τ)dτ.

Поэтому

σ(t) = c

∗

A(t−τ )

bξ(τ) dτ. (2.15)

Рассматривая описание блока L в виде (2.15), естественно приходим к следующему его

обобщению:

σ(t) = α(t) +

γ(t, τ) ξ(τ ) dτ. (2.16)

Здесь α(t) — непрерывная l-мерная вектор-функция из некоторого функционального мно-

жества {α(t)}, которое называют множеством собственных выходов (собственных процес-

сов, собственных колебаний) блока. В теории интегральных операторов матрицу-функцию

γ(t, τ) размерности l × m называют ядром интегрального оператора

γ(t, τ) ξ(τ ) dτ.

К описанию вида (2.16) приводится также описание блоков (2.14), когда матрицы A и b

зависят от t. В дальнейшем будем рассматривать только случай разностного ядра

γ(t, τ) = γ(t − τ ).

Обычно в теории управления такое ядро γ(t) называется импульсной переходной функ-

цией блока. Часто преобразование

γ(t − τ)ξ(τ) dτ

называют преобразованием свертки.

Итак, среди рассмотренных выше описаний блока L наиболее общим описанием является

описание (2.16). В случае когда имеется описание (2.14), получаем

α(t) = c

∗

, γ(t, τ) = c

∗

A(t−τ )

Остановимся теперь на вопросе о том, в каком смысле понимается линейность всех

упомянутых выше описаний блока L. Для описания (2.10), (2.13) и (2.14) можно было

говорить о линейности блока, поскольку все входящие в описание уравнения линейны.

Однако более естественно ввести другое определение линейности, под которое подпадает

и описание (2.16).

Определение 2.1. Блок L назовем линейным, если любой линейной комбинации любых

входов ξ

(t) и ξ

(t)

(t) + µ

(t)

соответствует линейная комбинация выходов минус µ

(t) + µ

(t):



(t) − α

(t)



+ µ



(t) − α

(t)



Здесь

(t) = α

(t) +

γ(t, τ) ξ

(τ) dτ.

Поскольку описания (2.10), (2.13) и (2.14) блока L могут быть сведены к форме (2.16),

а описание (2.16) очевидно линейно, то в силу приведенного здесь определения описания

(2.10), (2.13) и (2.14) также линейны.

§ 2.2. Передаточные функции и частотные

характеристики линейных блоков

Для линейных блоков, задаваемых уравнениями (2.10) или (2.13), определим переда-

точную функцию следующим образом.

Определение 2.2. Передаточной функцией W (p) линейного блока называется дробно-

рациональная функция

W (p) = −

M(p)

N(p)

, (2.17)

заданная на комплексной плоскости C.

Определение 2.3. Передаточной функцией линейного блока, задаваемого уравнениями

(2.14), называется l × n-матрица

W (p) = c

∗

(A − pI)

−1

b, (2.18)

элементами которой являются дробно-рациональные функции, заданные на комплексной

плоскости C.

Ясно, что передаточная функция (2.17) определена всюду за исключением точек C,

которые являются нулями полинома N(p). Эти особые точки являются полюсами дробно-

рациональной функции W (p). Аналогичное суждение имеет место и для W (p), заданной в

виде (2.18). Из правила обращения матриц получаем, что элементами матрицы (A −pI)

−1

являются выражения

(p)

α(p)

, i = 1, . . . , n, j = 1, . . . , n,

где α(p) — характеристический полином матрицы A: α(p) = det(pI − A), а α

(p) —

некоторые полиномы, степень которых не превосходит n −1. Поэтому в рассматриваемом

случае элементами W (p) являются дробно-рациональные функции

(p)

α(p)

, i = 1, . . . , l, j = 1, . . . , m.

Полюсами этих функций являются нули полинома α(p). Другими словами, полюсы W (p)

здесь совпадают с собственными значениями матрицы A.

Для корректности определений 2.2 и 2.3 необходимо показать, что если уравнения (2.10)

и (2.13) переписать в виде (2.14), то передаточные функции из определений 2.2 и 2.3

совпадут друг с другом. Для доказательства этого факта вспомним, что в данном случае

матрицы A, b и c имеют вид

A =







0 1 0 0 . . . . . . 0

0 0 1 0 . . . . . . 0

0 0 0 1 0 . . . 0

0 0 0 . . . 0 1

−N

. . . . . . . . . . . . . . . −N

n−1







b =













, c =













. (2.19)

Для таких матриц A, b, c имеет место следующая формула:

∗

(A − pI)

−1

b = −

+ M

p + . . . + M

det(pI − A)

. (2.20)

В самом деле, из вида вектора b следует, что для вычисления выражения (A − pI)

−1

необходимо вычислить лишь последний столбец матрицы (A −pI)

−1

. Из правила обраще-

ния матриц вытекает, что этот столбец составлен из алгебраических дополнений последней

строки матрицы

−







p −1 0 . . . 0

0 p −1 0 . . . 0

0 . . . 0 p −1

. . . N

n−2

n−1

+ p)







поделенных на det(pI − A).

Легко видеть, что искомые алгебраические дополнения равны −1, −p, . . . , −p

n−1

. Поэто-

му

(A − pI)

−1

b = −

det(pI − A)







n−1







Отсюда сразу следует формула (2.20).

Поскольку легко видеть, что

det(pI − A) = p

+ N

n−1

+ . . . + N

окончательно получим равенство

∗

(A − pI)

−1

b = −

M(p)

N(p)

(2.21)

для матриц, заданных в форме (2.19).

Отметим здесь очень важное свойство передаточной матрицы системы (2.14).

Т е о р е м а 1.1. Передаточная матрица W (p) инвариантна относительно неособых

линейных замен x = Sy (det S 6= 0).

Д о к а з а т е л ь с т в о. Выполним линейную неособую замену в системе (2.14) вида x =

Sy. В результате такой замены получим новую систему

= S

−1

ASy + S

−1

bξ,

σ = c

∗

Sy.

(2.22)

Составим передаточную матрицу этой системы:

(p) = c

∗

S(S

−1

AS − pI)

−1

Поскольку

−1

AS − pI)

−1

= (S

−1

AS − pS

−1

= (S

−1

(A − pI)S)

−1

= S

−1

(A − pI)

−1

получим, что

∗

S(S

−1

AS − pI)

−1

b = c

∗

(A − pI)

−1

Таким образом, передаточные матрицы W (p) системы (2.14) и W

(p) системы (2.22) сов-

падают.

Из формулы (2.21) и инвариантности передаточных функций относительно линейных

замен следует корректность определений 2.2 и 2.3.

Рассмотрим теперь линейный блок вида (2.16) с разностным ядром

γ(t, τ) = γ(t − τ ).

Для определения передаточной функции такого блока необходимо ввести преобразова-

ние Лапласа. Для этого рассмотрим множество вещественных непрерывных на [0, +∞)

функций {f (t)}, удовлетворяющих следующим неравенствам:

|f(t)| ≤ ρ e

æt

∀ t ≥ 0. (2.23)

Здесь число ρ может быть свое для каждой функции из множества {f(t)}, а число æ —

одно и то же для всего множества {f(t)}.

Определение 2.4. Преобразованием Лапласа называется оператор, заданный на мно-

жестве {f (t)} и отображающий каждый элемент этого множества в множество ком-

плекснозначных функций {g(p)}, заданных на множестве



p | p ∈ C, Re p > æ



(2.24)

по следующему правилу:

g(p) =

+∞

−pt

f(t) dt. (2.25)

Из неравенства (2.23) очевидным образом следует сходимость интеграла (2.25).

Естественным образом это определение распространяется на вектор-функции f (t). В

этом случае под абсолютной величиной | · | в левой части неравенства (2.23) следует по-

нимать евклидову норму | · |. В этом случае g(p) также являются вектор-функциями,

размерность которых совпадает с размерностями вектор-функции f(t).

Сформулируем здесь два важных свойства оператора Лапласа, обозначив этот оператор

через L: {f (t)} → {g(p)}.

Предложение 2.1. Если функция f(t) из множества {f (t)} имеет непрерывную про-

изводную в каждой точке t, то для

f(t) также может быть определен оператор Ла-

пласа по формуле



f(t)



+∞

−pt

f(t) dt,



f(t)



= pL(f (t)) − f (0). (2.26)

Доказательство этого утверждения состоит из следующей цепочки равенств:

+∞

−pt

f(t) dt=e

−pt

f(t)



+∞

+ p

+∞

−pt

f(t) dt= − f(0) + pL(f(t)).

Таким образом, можно распространить оператор Лапласа с множества {f(t)} на мно-

жество {f(t)} ∪ {

f(t)}.

Однако следует помнить, что интеграл

+∞

−pt

f(t) dt

не всегда будет сходиться абсолютно.

Предложение 2.2. Для функций f

(t) и f

(t) из множества {f (t)} справедлива фор-

мула



(t − τ) f

(τ) dτ



= L(f

(t)) L(f

(t)). (2.27)

Доказательство этого утверждения состоит из следующей цепочки равенств:



(t − τ)f

(τ) dτ



+∞

−pt

(t − τ)f

(τ) dτ dt =

Ω

−pt

(t − τ) f

(τ) dt dτ =

+∞

(τ)

+∞

−pt

(t − τ) dt dτ =

+∞

−pτ

(τ)

+∞

−pt

) dt

dτ =

+∞

−pτ

(τ) dτ

+∞

−pt

) dt

= L(f

(t)) L(f

(t)).

Здесь t

= t−τ, и область Ω имеет вид, изображенный на рис. 2.5, где Ω — сектор, располо-

женный в первом квадранте, границами которого являются ось абсцисс и биссектриса пря-

мого угла

τ = t.

Рис. 2.5

Заметим, что все несобственные интегралы в этих равенствах абсолютно сходятся в силу

неравенства (2.23).

Легко видеть, что предложения 2.1 и 2.2 справедливы и для множества матриц-функций

или вектор-функций {f (t)}. В этом случае в формуле (2.27) следует предположить, что

(t) — k × m-матрица-функция и f

(t) — m × l-матрица-функция.

Применим теперь развитый здесь аппарат к анализу уравнений (2.13) и (2.14). При этом

заметим, что если рассматривать вход ξ(t), удовлетворяющий неравенству

|ξ(t)| ≤ ρ

∀t ≥ 0,

то легко видеть, что и для вектор-функции x(t), и для функции η(t) можно указать числа

, ρ

такие, что выполнены неравенства

|x(t)| ≤ ρ

, |η

(i)

(t)| ≤ ρ

∀t ≥ 0. (2.28)

Здесь i = 0, 1, . . . , n − 1.

В самом деле, для этого достаточно доказать лишь первое неравенство, а оно следует

из оценок

|x(t)| ≤ |e

x(0)| +



A(t−τ )

bξ(τ) dτ



≤ βe

λt

|x(0)|+

A(t−τ )

| |b| |ξ(τ)|dτ ≤ βe

λt

|x(0)| + β|b|ρ

λt

(æ

−λ)τ

dτ.

Здесь числа β и λ таковы, что

| ≤ βe

λt

∀ t ≥ 0.

Очевидно также, что из оценок (2.28) следует существование ρ

, для которого

|σ(t)| ≤ ρ

∀t ≥ 0. (2.29)

Конечно, оценки (2.28), (2.29) могут быть получены и другими способами, улучшены и

т. д. Для нас сейчас важно, что имеются оценки такого вида.

В этом случае, выбирая æ = max(æ

, æ

) и полагая начальные условия нулевыми:

x(0) = 0 или η

(i)

(0) = 0, i = 0, 1, . . . , n − 1, получаем в силу предложения 2.1 следую-

щие соотношения:

1) для уравнений (2.13)





η(t)



= L(ξ(t)),

L(σ(t)) = L



η(t)













N(p) L(η(t)) = L(ξ(t)),

L(σ(t)) = M(p) L(η(t)),



L(σ(t)) =

M(p)

N(p)

L(ξ(t)),

L(σ(t)) = −W (p) L(ξ(t));

(2.30)

2) для уравнений (2.14)

L( ˙x(t)) = L(Ax(t) + bξ(t)),

L(σ(t)) = L(c

∗

x(t)),



pL(x(t)) = AL(x(t)) + bL(ξ(t)),

L(σ(t)) = c

∗

L(x(t)),



L(x(t)) = −(A − pI)

−1

bL(ξ(t)),

L(σ(t)) = c

∗

L(x(t)),



L(σ(t)) = −c

∗

(A − pI)

−1

bL(ξ(t)),

L(σ(t)) = −W (p) L(ξ(t)).

(2.31)

Таким образом, нами установлена очень простая связь между преобразованиями Ла-

пласа входа и выхода линейного блока.

Если рассмотреть теперь описание линейного блока (2.16) с разностным ядром γ(t, τ ) =

γ(t − τ):

σ(t) = α(t) +

γ(t − τ) ξ(τ ) dτ, (2.32)

предположить, что начальное состояние блока таково, что α(t) ≡ 0, и воспользоваться

предложением 2.2, то получим равенство, аналогичное равенствам (2.30) и (2.31):

L(σ(t)) = L(γ(t)) L(ξ(t)). (2.33)

Поэтому естественным представляется следующее определение.

Определение 2.5. Передаточной функцией (матрицей-функцией) W (p) линейного бло-

ка, описываемого уравнениями (2.32), называется преобразование Лапласа γ(t), взятое с

обратным знаком:

W (p) = −L(γ(t)). (2.34)

Корректность определения следует из того факта, что для уравнений (2.14) γ(t) =

∗

b, и поэтому

L(γ(t)) = L(c

∗

b) =

+∞

−pt

∗

b dt =

= c

∗

(A − pI)

−1

(A−pI)t



+∞

= −c

∗

(A − pI)

−1

Здесь мы воспользовались соотношением

lim

t→+∞

(A−pI)t

= 0,

которое следует из предположения, что Re p > æ > max

Re λ

(A). Здесь λ

(A) — собствен-

ные значения матрицы A.

Заметим, что передаточная функция W (p), определенная соотношением (2.34) для ин-

тегральных операторов (2.32), не всегда является дробно-рациональной, как это имеет

место в случае операторов (2.13) и (2.14).

Перейдем теперь к определению частотной характеристики линейного блока. Для этого

предположим, что æ < 0, и, следовательно, передаточная функция (матрица-функция)

определена также и на мнимой оси.

Определение 2.6. Функция W (iω) называется частотной характеристикой линей-

ного блока.

Наряду с преобразованием Лапласа важную роль во многих разделах прикладной ма-

тематики играет преобразование Фурье.

Часто в теории управления преобразование Фурье определяется так, чтобы оно совпа-

дало с преобразованием Лапласа на мнимой оси: p = iω, т. е.

F (f(t)) =

+∞

−iωt

f(t) dt. (2.35)

Такое определение содержится, например, в книге [17].

В классическом анализе (см. [30]) преобразование Фурье для функций f(t), заданных

на (−∞, +∞), определяется как

F(f (t)) =

√

2π

+∞

−∞

iωt

f(t) dt. (2.36)

Сравнивая (2.35) и (2.36), можно в (2.35) доопределить f (t) ≡ 0 на (−∞, 0), и тогда

образы (F (f))(iω) и (F(f))(iω) одной и той же функции f (t) оказываются связанными

соотношением

(F (f))(iω) =

√

2π (F(f))(−iω). (2.37)

Такое различие в определениях является, как правило, несущественным, и использо-

вание того или другого определения обосновывается только удобством изложения. Здесь

будет удобнее использовать определение (2.35).

Из формул (2.30), (2.31), (2.33) сразу следует, что при нулевых начальных состояниях

блока

F (σ(t)) = −W (iω) F (ξ(t)). (2.38)

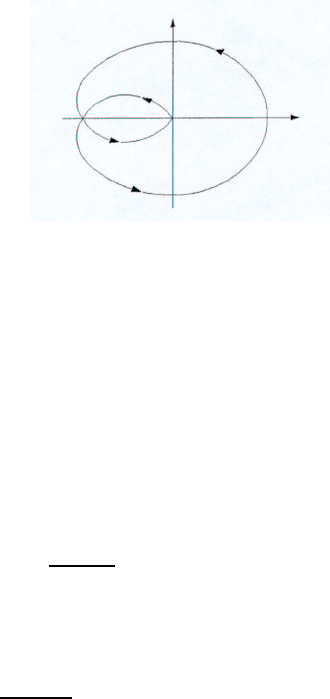
Определение 2.7. Годографом частотной характеристики W (iω) называется мно-

жество всех ее значений на комплексной плоскости C.

На рис. 2.6 приведен пример годографа W (iω). Стрелками указано направление, по

которому движется значение W (iω) при возрастании ω.

Рис. 2.6

x Рассмотрим теперь случай, когда вход ξ(t) является чисто гармоническим. Ограни-

чимся здесь описаниями блоков (2.13) и (2.14) с m = l = 1. Нам удобно также записать ξ(t)

в следующем виде: ξ(t) = e

iωt

. Будем искать решения η(t) и x(t) в виде η(t) = V (iω)e

iωt

x(t) = U(iω)e

iωt

, где V (iω) — скалярная и U(iω) — векторная величины. Подставляя эти

выражения в уравнения (2.13) и (2.14), получаем

V (iω) N(iω)e

iωt

= e

iωt

(A − iωI) U(iω)e

iωt

+ be

iωt

= 0.

Эти соотношения будут выполнены, если

V (iω) =

N(iω)

, U(iω) = −(A − iωI)

−1

b. (2.39)

Таким образом, существуют чисто гармонические решения η(t) и x(t), и выход σ(t) в

силу (2.39) имеет вид

σ(t) =

M(iω)

N(iω)

iωt

, σ(t) = −c

∗

(A − iωI)

−1

iωt

Введя частотную характеристику W (iω), окончательно получим

σ(t) = −W (iω) e

iωt

. (2.40)

Таким образом, при ξ(t) = e

iωt

существуют начальные состояния блоков, при которых

выход σ(t) определяется по формуле (2.40).

Ограничимся рассмотрением случая устойчивых блоков, т. е. будем рассматривать блок

(2.13), когда N(p) — устойчивый полином, и блок (2.14), когда A — устойчивая матрица

(т. е. все ее собственные значения имеют отрицательные вещественные части). В данном

случае для двух решений x

(t) и x

(t) с разными начальными условиями x

(0) и x

(0)

имеем



(t) − x

(t)



•

= A



(t) − x

(t)



Из свойств матрицы A сразу получаем, что

lim

t→+∞



(t) − x

(t)



= 0.

Отсюда следует, что и для соответствующих выходов σ

(t) и σ

(t) также имеет место

равенство

lim

t→+∞



(t) − σ

(t)



= 0. (2.41)

Так как уравнения (2.13) являются частным случаем описания (2.14), получаем, что (2.41)

справедливо и для описания блока (2.13).

Из (2.40) и (2.41) следует, что для устойчивых блоков при ξ(t) = e

iωt

и любых начальных

условиях

lim

t→+∞



σ(t) + W (iω)e

iωt



= 0. (2.42)

Из формулы (2.42) следует, что для устойчивых блоков частотную характеристику можно

определять экспериментально. Для этого нужно на вход блока подать гармонический сиг-

нал ξ(t) = e

iωt

. После этого подождать некоторое время, пока на выходе не установится

некоторый гармонический сигнал

σ(t) = A(iω)e

iωt+α(iω)i

Здесь A(iω) — вещественная положительная величина, A(iω) является амплитудой сигна-

ла, α(iω) — сдвигом его по фазе. Ясно, что

A(iω) = |W (iω)|, α(iω) = π + arg W (iω).

По этим формулам однозначно определяется комплексное число W (iω). Прогоняя ω от

−∞ до +∞, получаем годограф W (iω). (На самом деле, из-за очевидного свойства

lim

ω→+∞

W (iω) = 0

необходимо проводить эту прогонку только на конечном промежутке изменения ω).

Таким образом, для получения указанным путем частотной характеристики не нужна

информация о коэффициентах полиномов M(p) и N(p) или о матрице A и векторах b

и c. Поскольку многие результаты в теории управления формулируются в терминах ча-

стотных характеристик, то для них не требуется описание блоков дифференциальными

или интегральными уравнениями, а нужна кривая на комплексной плоскости, которая

является годографом частотной характеристики.

Часто оказывается, что частотная характеристика позволяет однозначно определить

такие уравнения. Пусть, например, априори известно, что полиномы M(p) и N(p) в опи-

сании (2.13) не имеют общих множителей. Тогда по W (iω) однозначно определяется W (p)

(принцип аналитического продолжения), а по дробно-рациональной функции W (p) одно-

значно (с точностью до общих множителей) определяются полиномы M(p) и N(p).