Леоненко Н.Н., Иванов А.В. Статистический анализ случайных полей
Подождите немного. Документ загружается.


00
П
р
и
v>
- 1/2
обоз
нач
и
м
J,.(z) =
~
(-
l)m(z/2)2m+,' )<
11'1=
0
х
[
m
1
Г
(m
+,'+
I)
Г
\
ф
у н
к
ци
ю
Бе
с
с
е
л
я
перв
о
г
о
р
о
д
а
п
ор
я
д
к
а
",
а
У
n (z) = 2
(,,-2\
/21' (n/2) J(,,_ 2)/2
(
г
)
р
-п
)/2
сфер
и ч
е с
кую
бе
с с е
л
е
ву
ф
у
нк ц
ию
.
Д
л
я
тог
о
чт
о
бы ФУ
ШЩИЯ
В
(р)
,
р
Е
R~
б
ы
л
а
к
.
ф
.
о
д
но
ро
дног
о
и
зо
т
р
о
п
н
о
г
о
с
.
к.
не
прерывного
слу
ч
ай
н
о
го
п
ОЛЯ
~
(
х
)
.
х
Е
к:
н
е
о б
х о
д
им
о
и
д
о
с
т
а
т о
ч
н
о
,
чтобы
на
и
з
м
е
ри
м
о
м
пр
о
с т
р
а
н
с т
в
е
(
R
~
,
~
(
R
~)
)
с
у
щ
ес т
в
ова
л
а
коне
ч
н
а
я
м
ер
а
0(
· )
т
а
к
а я
,
чт
о
со
(1.2.4)
B(r) =
~
У
,.
(ир)
О
(du),
( ,
пр
и
че
м
О
(R
~
)
= F (R") =
В
(
О
)
<
00
.
О
г
ра
н
и
ч
е
н
н
ая
н
еу
бы
в а
ющая
ф
ункция
О
(и
)
= ,) F (
d')..)
P.:I"-\
<uf
н
а з
ы
в
а
е
т
с
я
с
пе
к т
ра
ль
но
й
ф
ун
кц
и
е
й
о
д
н о
родног
о и
з
отропн
ого
с
л
у
ч
а
й
но
го
п
оля
.
Я
сн
о,
что
r
00
dO
(
и
)
= F (R") <
00
,
прич
е
м
о
сущ
е
ст ву
ет
ф
орм
у л
а
об
ра
ще
н
и
я
00
I
О
(и)
=
2
(
2
-
,,
)
/2г
-
(n/2)
~
J
,,
/2
(
и
г
)
(иг)
П
/
2
в
(г)
г-
1
dr. (1.2.5)
о
Т
а
к
.
при
п
= 2
фо
рму
ла
(1.2.4)
имеет
вид
00
(1.2.6)
в
(Р)
=
J'
J
о
(и
р)
О
(du).
о
а
п
р
и
п
= 3
00
(1.2.7)
В
(р)
= 2
~
sin
{ир}
(
и
р
г
1
О
(du).
о
Ф
о
р
му
л
а
(1.2.4)
выт
ек
ает
из
(1.2.1),
если
перейти
к
с
фе
ри
ч
е с
к
и
м
ко
ордин
а
т
ам
(1.1. 1)
и
в
осп
о
льзовать
ся со
о
т
но
ш
е
н
и
ем
\ 5
/1
_ 1
(и
)
г J
е
l
(
Л
'
Х
-
У
dm
(
л.)
=
У
п
(
и
l
х
-
У
i
)
,
( 1.2.8)
'n_l(U
)
г
д
е
т
(.) -
мера
Л
е
бе
га
н
а
сфе
ре
5
п
_
1
(
и)
(
с
м
.
(1. 1. 2)).
З
а
м
еч
ание
1.2.1.
Е
с
ли
В
(О)
= 1,
т
о
0 (·) -
вер
оятн
о
ст
н
ая
18
м
ер
а
на
R
~
.
П
р и
n
>]
р
а
с
с
мо
т
рим
си
мм
ет
р
и
ч
н
у
ю
м
еру
на
1-
- 1. 1]
0
(,,_
2
)
r
2(du)
=(l-u
~
)
(
,,
-
;!
)
/
2
1!
/n
Г
«n-
I
)
/
2
)г
I
Г
(
n
/
2
)
d
и
.
и
Е
r- 1, 1].
И
с
п
о л
ьз
у
я
инт
ег
р
а
л
П
у
а
с с
о
н
а
1
I
/
2
J"
(г
)
г
(v + 1/2) =
л
-
(z.l2
)v J
е
"
2
(1 - {2)" - 1/2
Jt
.
Re v>
-1/2,
-1
(1.2.9)
нах
оди
м
,
чт
о х
.
ф
.
ра
с
п ре
де
л
е
н
и я
0 (,,- 2)/2
р
а
в
н
а
У
"
(t),
и
,
с
л
е
до
в
а
т
е
л
ь
но
,
ф
ор
м
у
ла
(1.2.4)
м
о
ж
е
т
быть
з
а
п
и с а
н
а
в в
и
д
е
В
(t)
=
Л1
У
"
(t l))
=
М
е
х р
{
itYJ
'
~
}
'
гд
е
11
и
~-
н
е
з
а
в и
с
и
м
ы
е
С
.В
.С
р
аспре
д
е
л
е
ни
я
м
и
о
и
0(
,,
- 2'
/2
соо
т
в
с
тс г
в с
ино
.
С
д
р у
г
о
й
сто рон
ы
,
на
(1.2.4)
м
ожн
о
с
мот
реть
к
а
к
н
а
п
р
е
обр
азо
в
ан
и
е
00
га
н
к е
л
е
во
г
о
т
ип
а
Н
"
(
О
,
t) =
В
(t) =
~
У,
.
(и
t)
О
(du)
с я
д
ро
м
о
у
v (t) =
Г
(v + 1) Jv (t)
(t
/2Г
V
,
к
отор
о
е
оп
р
е
деле
но
при
\'
>-1
/2
(и
ли
n>
\).
Однако
при
,,
-+
- 1/2 + 0
l i
ш
У
v
(
t )
=
с
о
s
t
,
а
фун
кц
и
я
cos t
является
характ
ери
стич
е
ск
ой
ф
у н к
ц
ие й
ве
ро
я т
н
о
ст
ной мер
ы Е
=(
е
1
+
е
_
)/
2
,
сос
ре
до
то
ч
ен
н
о
й
в
точках
1
и
1
-
Г
с
м
ассо
й
1/2
в
каждой
и
з
н
их
.
П
о
эт
ом
у
мо
ж
но
о б
о
з
на
чить
cos t
через
У
-1
/2 (i).
а
м
еру
Е
че
ре
з
0
-1/2
( .)
и
п
о
не
прерывн
о
сти
считать
v
~
- 1/2,
в
к
л
ючив
в
расс
мо
т
ре
н
и
е р а
з
м
ерн
ость
п
= 1.
Л
е
м
ма
1.2.1.
Если
В
(р),
р>
О
-
к
.
ф
.
С
.
к.
н
епрерывного
од
но
ро
д
но
г
о
из
отр
опн
ог о
случ
айн
ог
о
п
о
ля, т
о
:
1)
В
(Р)
>-
В
(О) /n;
2)
п
ри п
~
3
фу
н
к
ц
и я
В
(Р)
к
а
к
фу
нкци
я
р
д
и
ф
ф
е
р
е
н
ц
и
р
у
е
м
а
[(n - 1)/2]
раз.
...
*
П
у
с
т ь
x
(j
)ER
",
j=
1
....
'
n+
1,
п
р
и ч
е
м
Ix
(
I)-Х
(]
)I=
,,
+1 ]2
=р,
i=l=i .
Т
о
г
д
а
М
j
~
~(x
(j
»)
= (n + 1)
[В
(
О
)
+
n
В
(р)
) ,
[
о
тк
у
д
а с
л
е
д
у
е
т
1)
.
Соо
т
но
ш
е
н
и е
2)
с
л ед
у
е
т
из
т
ог
о
,
ч
т о
(].2.4)
м
о
ж
н
о
д
и
ф
ф
е
р
е
н
ц
и
ров
а
т
ь
п о
Р
со
гл
ас
н о
фор
м
уле
(d/dz)
Х
Х
{J
v
(
г)
г
-
"}
= - J
v
+
1
(z)
«",
пр
и
ч
ем
и
н т
е
г
р
а
лы
,
п о
л
ученны
е
фо
р
ма
л
ь
н
ы
м
дифференцир
о
в
ани
ем
,
сх
о
д
я
т
с я
равномер
но
. •
П
у
с
т
ь
n > 2
и
(
г
,
и),
и
Е
S,,_I
(1),
г
~
0 -
с
ф
е
р и
ч
еск
и
е к о
ординаты
то
чки
х Е
R"
(см
.
(1.
1.1
)).
О
б о
з
начи
м
че
рез
з;
(и)
.
и
Е
5,,_1 (
1)
ве
щественные сф
е
р
и ч
е
ск
и
е
г
арм
о
н и
ки
степе
ни
т,
h (n,
т)
=
(
2
т
+
п
- 2)
(т
+
п
- 3)1/[(n - 2)1ml)
чи
с
л
о
так
и
х
гарм
о
ник
[5,
с.
2 2
5-240;
27,
с
.
431
-4
67].
Ис
польз
у я
те
о
р
ем
у
Кар
у и
ен
а и
т
е
ор
е
м
у
с
ло
же
н
и я
бессе
л
е
•
Знач
о
к
"
у к
а
з
ы
в
а
е
т
начало
д
ока
з
а
т
е
л
ь с
т в
а
,
а
1;1-
е г
о
к
онец.
2·
19

вых
ф
у
нкц
ий
2(n-
2
)
/2
г
(n/2) J (n - 2)(2
(Vr
t +
Г
~
-
2г
1f2CO
S
у)
Х
со
h
(n.
m l
Х
И
+
г~
-
2
г
1f2COS
у)
(
2
-n
)
/2
=
СТ
(n)
~
~
5
~
(
и
1
)
5
~
,
(
и
2
)
х
т
=
О
1=1
Х
J
m
+ (1I- 2)/ 2
(Г
)
) ", +(n - 2)/2
(Г
2
)
(г
1г
2
)
(
2
-
n
)
/2
.
1
г
де
х
=(г
1
•
и
)
,
у
=
(г
2
,
и
2
)
,
Uj E
sn
_I(I),
Г
>
1,2,
со
з
т
=
1
=
(х
,
у
}
/
[
I
х
"1
у
1] -
к
ос
ин
ус у
г
л
а
ме
жд
у
х
и
у,
\
х
-
у
I =
=
1/ '
г1
+
Г
~
-
2г
1f2COS
у
,
а
СТ
(n) =
2
"
-
'
Г
(n/2)
пn
12
,
(1.2. 1
О
)
по
лучаем
дл
я
по
л
я;
(
х
)
,
х
Е
R
n
т
а
к
ое
с
п
ек
т
р
а
ль
ное
р
а
зл
о
ж
ениеl
со
h(n .m)
00
~
(х)
=
01
(n)
~ ~
5~
,
(и)
J) ", +
(n-
2)/2
(/-Lr)
(
~
t
г
г(
n-
2
)
122~
(ф
l)
.
т
:=
О
1= 1 IJ
(1
.2.1 1)
В
ф
ор
муле
(1.2 .11)
ря
д
с
хо
д
и
т
с я
в
с
р
е
д
не
м
к
в а
д
р
а
т
ич
е
с
к о
м
а
2;"(
.)
-
се
м
ей
с
т в
о
в
ещ
е
ст
в е
нных
сл уч
а
й н
ых
м
е
р
н
а
(
R
~
,
\8
(
R
~
) )
т
а
к и
х
,
чт
о
вып
о
лнен
ы
соот
но
ш
е
н
ия
:
1)
M
2
~
(6) =
О
;
2)
M2~
1
(6 1)
2
~
(6
2)
=
6
~n
6
1
C
(6 1n6
2)
*, 6, 61' 62
Е
)5
(R
~)
.
П
р
и
n = 2
С
(n) = V 2n,
11
(т
,
2) = 2
д
ля
к
а
ж
д
ог
о
т
Е
21
1
с
у
щ
е
с
тв
у
ю
т
д
ве
ком
п
лек
с
ные
г
ар
м
оник
и
:
ехр
{im
(j)
}/V 2n
и
ех
р
{
-
i
m
Ч'}
/
V
2
п,
в
т
е
р
м
ин
а
х
которых
п
р
е
д
ст
а
в
л
е
н
и
е
(1.2. 11)
м
о
ж
н
о
п
ер
е
п и
с а
т
ь в
ви
де
00
00
lт
ф
r
(1.2.12)
~
(
г
,
Ч'
)
= ~
е
j J
т
(/-Lp
)
2
т
(d
~ t
),
т
=-
ОО
о
гд
е
)т
(z)-
ф
у
н
к
ц
и
я
Б
е
с
се
л
я п е
р
в о
г
о р
о
д
а
ц
е
ло
г
о п о
р
яд
к
а
т
;»
О
,
J_
m
(z) = (- I)mJ
m
(2),
а
2
т
(.) -
компле
кс
ные
сл
у
ч
а
й
п
ы
е
м
е
р
ы
,
т
а
к
и
е
,
ч т о
М2
m
(61)
2
т
,
(6 2) =
6;;:
'0 (61n62)
,6
1'
6
2
Е
Е
~
(R~
)
,
а
(
.)
у
ч
а с
т
в
у
е т в
(1.2.6).
П
р
и
п
= 3
п
о
ле;
(
Х
),
х
=
(
г,
ер
,
СР
l
)
Е
R
3
,
Г;;;:
О
,
О
~
ерl
<
п,
О
~
ер
<
2п
мож
е
т
б
ыт
ь
пр
е
дст
а
вле
но
рядом
00
т
00
~
(
г
,
ер, ер
l
)
=
л
V2
~
~
5~
(<р,
(j)1)
j
)m
+ l/2
(!!Г
)
х
т=
-ОО
I=
- m U
- 1/22 1 )
(1.2.13)
х
(/-Lf
)
т
(d/-L
,
• 6
':
= 1. r =
т;
О
,
r +
т
-
сим
в
ол
К
рон ек
е
р
а
.
20
г
де
2~
(.) -
ко
м
п
лек
с
ные
с
л у
ч
айны
е
м
еры
с
о
с
тр
у к
т
ур
н о
й
фу
н
кц
ие
й
а
(.)
из
(1.2.7),
а
ко
мплек
с
ные
сфе
р
и
чес к и
е
гармо
ники
) il
q>
e
l
I
Г
-
1
5
m
1
(ер
,
ерl
=
е
~т
(со
э
о
.)
,
V
2
л
,
-
т
~
~т
,
e~
(
х)
= k
(т,
1)
(1 - X
2
) 1/ 2 (dl
+m
/d
/+
m
) (1 _
х
2
)
m
=
1
= k
2
(т
,
1)
(1 -
х
2
г
l
/
2
(
dm
- I/dx
m
-
I)
(1 -
х
2
)
т
,
1>-
О,
е;;
1
(
х)
= (-
1)
l
e
~
(
х),
S;n
(
ер,
СР
l
)
= (- 1
)15
;;;
1
(
ср,
Ч'
l )
'
k]
(
т,
1) =
(-
1)'"
V(2
m +
1)
(
т
- 1
)1
/[2
(т
+ 1
)1]
[2"'m
!
г
l
,
k
2
(т
,
1)
=
(-
l)m-
1
1
/ (2m + 1)
(
т
+ l)!/[ 2
(т
- 1)1)
[
2
mmI
Г'
.
(1.2.14)
Ф
ун
кц
и и
5;n
(ср
,
(j)
1)
о
б л
ада
ю
т
свойств
ом
о
р
т
о
го
на
л
ь
н о
с
ти
:
r I .
l'
l'
т
'
J
5
т
~
cp,
СР
l
)
5
т
,
«
(j),
СРl)
а
т
,
«
(j)
,
(j)
1) = 6, 6
m,
(1.2.15)
5,(1)
гд
е
dm
«([>
,
ер
l
)
= sin
(j)
ld
rp
ld
cp
,
О
~
ep
l< n'
O~
cp
<
2
n
(с
м
.
(1. 1.2)).
Замеча
ние
1.2.2.
При
п
= 3
фу нкц
и
и
5
~
1
(Ч'
,
СР l)
в
ы
р
аж
а
ютс
я
ч
ер
ез
п р
и
с
о
е
д
и
н
е
н
н
ы
е
ФУ
Н
К
Ц
И
И
Л
е
ж
а
н
д
р
а
первого
р о
да
и
ли
ч
е
р
е
з
мн
о
г
о
ч
ле
н
ы
Г
е
г
ен
б
а
у
э р
а
[5,
с
.
241
- 243J.
П
о л
е
~
(х
)
,
х
Е
и
:
и
мее
т
а
бсо
лю
т
но
не
п
р
е
р
ы
в
ны
й
спе
кт
р
,
т
.
е
.
ме
ра
F
(.)
в
(1.2. 1)
а
б
с
олю
тн
о
не
п
р
е
ры
вн
а
относи
т
ел
ьн
о
лебеговой
ме
ры,
т
о
г
д
а и т
о
л
ь
к
о
тогда
,
когда
~
(
х
)
= I
ь
(
и
-
х
)
W (du), (1.2.16)
R
n
Г
де
Ь
(.)
Е
L
2
(R
n
),
W (.) -
ко
мп
лекс
н ая
в
инер
овскан
м
е
р
а
н
а
(R
n
, )5
n),
т.
е.
М
I w(6) [2= 161, 6
Е
)5n
.
В
п р
е
д
с
т
а
вл
ении
( 1.2. 16)
Ь
(х)
-
пр
ео
бра
зо
в
а
н
и
е
Ф
урье
--
П
л
а
п
ш
е р
е
л
я
ф
у
нк
ц
ии
а
(
л)
Е
L
2
(R
n
),
г
де
I
а
(л)
12 = t
(1.)
-
с
пе
ктра
л
ь
н
а
я
п
л
о
т н
о
с
т
ь
п
о л
я
;
(
х)
,
xE R
n
.
Е
с
л
и
Ф
УН
К
Ц
И
Я
Ь
(х
)
в
(1
.2.
1
6)
-р
а
д
н
а
ль н
ая:
Ь
(
х
)
=
Ь
(\
х
1),
то
п
о
л
е
~
(х),
х
Е
R
n
яв
ляетс
я
од
н
ород
ны
м
и
изотроп
ным
.
Е
с
л
и
~
(
х
),
х
Е
R
n
-
о
д
н
ор
о
д
н
ое
изо
т р
о
пн
о
е п
о
л
е
с
абсо
лю
т
но
не
п
ре
ры
в
ны
м
спе
к
тром
,
т.
е
.
с
у
ще
ст
ву ет
ф
у
нкц
и я
g (
/-L)
т
а
к
а
я
,
ч
то
a
/(/-L)
=
Is(I)I/-L
n-1
g(/-L),
fL
n
-l
g(/-L)
ЕL1(R
~),
(1
.2.17)
т
о
ф
ун
кц
и
ю
g
(р)
бу
д
ем
н
азы
ват
ь
из
отр
о
пно
й
с
пе
к
тр
а
л
ь
н
ой
п
л
о
тн
о
сть
ю
поля
~
(
х),
х
Е
R".
21

В
э т
о
м
с
л
у
ч а е
пр
е
д ста
вление
(1.2.4)
м
о
ж
н о
п
е
ре
п и
с
а
т
ь
таю
00
в
(р)
= 15(1 ) IS
у
n
(~
t
p
)
~
t
n-I
g
(
~
)
d~
(1.2.18)
о
С
пект
р
альн
о
е
пр
е
д
с
т
авление
(1.2 . 16)
в
этом
сл
уч
а
е
и
м
е
ет
вид
со
Jl{tJ ,m )
00
~
и
=
(2л:)
n
I
2
~ ~
5;"
(и)
j'
r (
l-n)
/ 2
V
~
) ", + (
11
- 2)/2
(flI
)
Х
m=
U
'~
I
О
Х
J/ g
(~L)
\
r
/ ~
!
(d!I),
(1.2. 19)
г
д
е
{
\
~
~
,
(.)
},
l = 1, ... , /1(
11
.
т),
т
=
О,
1, .., -
с е
м
е
й
с
т
в
о взаи
м
н
о
н е
кор
р е
ли
ро
ва
н
н
ы
х
ло
й
с
т
в
и
т
ель
н
ы
х в и
п
е
р
о
в
ск
и х
ме
р на
(R
~
.
Q.~
(/<~
)
),
т
.
е.
1\
1
\
J,:
/
~
!
(L\l) \\'Ih(
L\
2) =
6
~
!o,!
I
L\
1 n
L\2
1·
О
б
р
ати
м
в
ни
м
а
н
и е
на
с
л
е
д
у
ю
щ
и
е
обст
оя
т
е
л
ь
с
тв
а,
свя
з
а
нные
R
n
с
опр
е
д
е
л
е
ни
е
м
в
е
ктор
н
ого
сл
у
ч
ай
но
г
о П
О.
1Я
S: Q
х
-+
R"'
.
О
Д
Н
О
РОД
Н
Ы
С
Н
Ш
И
Р
О
К
О
М
см
ы
сле
слу
ча
й
н
ы
е п
о
т
!
Si :Q
х
х
R"
-+
R\
i = 1, 2
с
н у
л
ев
ы
м
и
сре
д
ни
ми
называются
одно
р
о
д
н о
св я
з
а
нн
ы
м
и
,
е
с
л
и и
х
вз
а
и
м
п
а
я
К
.
Ф
.
В
12
(
х
,
у
)
= M;t(X)
х
х
S2
(
у
)
=
В
1
2
(
х
-
у)
завис
и
т
лиш
ь
от разнос
т и
х
-
у
.
Од
н
о р
о
д
н о
с
в
я
з а
нны
е
с
л
у ча
й
н
ы
е
п
ол
я
и
з
о т
ро
п
но
с
вя
заны
,
есл
и
их
вза
и
м
н
а
я
к.
ф
.
8 12
(
х
-
у
)
за
в
ис
и
т
ли
ш
ь
от
ра
с
стояния
Р
ху
= I
х
-
у
1·
Со
во
к
упность
т
однородны
х
(и
з
о
т р
о
пных)
по
ле
й
;
(х
)
= [;1
(х),
..., S
Ill
(
х
)
]
,
однородн
о
(из
отр
опн
о)
св
я
з
анных
ме
ж
д
у
с
о
бо
й
,
назов
е
м
не
к
т
о
р
н
ы
м
о
д
н
ородным
(из
отр
опным)
с
л у
ч
а
й
н
ы
м
П
О.
'1
е~
1
; : Q
х
R"
-~
Р",
Пу
с
т
ь
В
г
•
(х)
= MS
r
(х
+
у)
;.
(у).
Т
о
г
да
м
а
т р
и
ц
а
В
(х)
=
=
(
В
Г
•
(x»)' .S= I. ...", -
к
.
ф
.
о
д
н
ородн
о
г
о
(И
З
О
ТРОП
НОГО)
ве
к
то
р
но
г
о
п
о
л
я
S: Q
х
R"
-+
Р
",
П
усть
В
(х
)
н
е
п
р
е
р
ы
в
н
а в
т
очке
х
=
О.
Т
огд
а
д л
я
в сех
г,
5
Е
{1, ...,
т
}
ф
ун
к
ц
и
и
В
" (
х
)
д
о
пус
кают
р
а
з
л
о
ж
е
н
и
е
( 1.2. 1)
в
случ
ае
од
н
оро
д
ного
по
ля
и
р
а
зл о
же
н
и е
(1 .2.4)
в
с
лу
ча
е
о
д
н
о р о
д
н о
г
о
из
о
т
ро
п
н о
г
о
поля
.
О
б
о
з
н
а
чи
м
ч
е
р
ез
с
г
•
(.)
с
п е
к
т р
а
л
ьн
ы
е
м
е
р
ы
,
у
ча
с
тву
ю
Р
г э
(
.)
.
щ
и е в
э
т
и
х
разло
ж
ен
ия
х
,
и
на
зове
м
м
атр
ич
ные
ме
ры
F =
=
(
Р
г
э
( •
),.
s= l.....
т
И
G =
(
С,в
(.
)'
.5
= 1.....
т
с
п
ектральн
ы
ми
м
ер
ам
и
ве
к
т
о р н о
г
о о
д
н
ор
о
д
ного
и
од
но
ро
д ного
изотр
опног
о
п
оля
R
n
~
:
Q
х
-+
Р"
соотв
етст
в е
н
но
.
Т
о
г
д
а
к.
Ф
.
В
(х
)
век
торн
ого
о
д
н
оро
д
но
г
о
(
и з
о
тро п н о
г
о
)
сл
у
ч а
й
н
о
г
о
поля
доп
у
скает
р
азл
о
ж
е
ни
е
(J .2.])
(
со
о т
вс
т
с
т
ве
п
н
о
(J .2.4) ,
в
к
отор
ы
х
F (.)
и
G(.) -
м
ат
р
и
ч
н
ы
е
ме
р
ы,
о
п
ре
д
е
л
ен
н
ы
е
выше
.
В
с
л
уч
а
е,
когд
а
в
се
э л
е
м
е
н
т
ы Р
с
в
(.)
м
а
т
р
и
ц
ы
F
аб
с
о
лют
но
н е п
р
е р
ы
в
н
ы
о
т н
ос
и
т
ел
ь
н о
л
е
б
е
г
ов
о й
м
е
р
ы
,
та
к
чт
о
с
у
ще
с
т
в
у
ю
т
',
в
(i.) =
(
д
"
/
д
Л
[
.. .
...
ai.
n
)
р
, в (
П
(-
00
,
Л,
»
)
,
г,
5 = 1, ..,
.
т
,
говорят,
ч
т
о
м
н о
г
о
м
е
р
н ое
п
о
л
е
s:Q
х
Р
"
-+
Р"
и
м
е
е
т
спектраль
н
ую
плотн
о
сть
f
(л)
=
=
(f
rB
(
л
) ) '
.
s
=
I
.....
т
'
В
эт
о
м
с
л у
ч а
е
к.
ф
.
д
о
п
у
с
к
а
е
т
ра
зложение
(1.2 .2),
в
ко
т
ором
t (i.)
над
о
пони
мат
ь
как ма
т
ри
ч
н
о
з
н
а ч
н
у
ю
ф
у н
кцию,
о
п
р
е
д
е
л
е
н н
у
ю
в
ыше.
Т
а к
же
вв
о
д
ятся
вект
орны
е а
на
ло
г
и
и
други
х п
о
н
ят
и
й
,
о
п
ределен
ных
ра
нее
д
л
я
с
к
а
ля
р
н
ы
х
по
ле
й
.
1.3.
О
С П
Е
КТРА
ЛЬ
Н
Ы
Х
С
В
Ой
С
Т В
А
Х
С
ТА
Р
Ш
И
Х
М
О
М
ЕНТ
О
В
СЛ
У
Ч
А
й
Н
Ы
Х
П
О
Л
Е
И
В
ве
д
е
м
классы
Форте
и
Бл
ан
-
Л
а
пьерра
дл
я
сл
у
ч
айны
х
полей
.
R
II
П
у
с
ть
т
(
т
)
-
к
л
а
сс
с
лу
ч
а
й
н
ых
пол
ей
S: Q
х
-+
Ю
,
д
Л
Я
к о т
о
р
ы
х
М
Is
(х)
1
т
~
k
m
<
00,
г
де
km>O
-
по
с
т о
я н
н
ы
е
,
т
>
1
ц
е
л
о
е
числ
о
.
М
о
м
с
н т н
ые
и
с
е
м
иинв
ар
иантн
ы
е
ф
у
н
к
ц
и
и
[юля
S
(
х)
Е
Т
(
m
)
п
о
р я
д
к
а
r
Е
{Г,
2, ...,
т
}
обозначим
си
м
в
ол
ами
т,
(х(1
) ,
... ,
ХИ)
=
М
П
;
(х
'
")
,
5, (X (I),
...
,
х
(
о
)
=
i=1
=
i
-
'(д
'
/
да
1
•• •
aar)ln
MexP{i
~
a
j
;
(
x
(j)
]
1
.
(1
.3.1)
j= l J
(11
= ..·= (1, = 0
Е
с
л
и
это
необход
и
м
о
,
б
у
д
е
м
сн
а
бж
ать
з
а
п
и
с
ь ве
р
х н
и
м
и
и н
д
е
к
са
м
и и
писать
m~~)
(. ),
5~
~)
( . ) .
Оч
евидн
о,
т,
(х(1),
... ,
х
(
о
)
.
s(r)
(X(I)
• .
..
,
х
И
)
являются
с
и
м
метричны
м
и
Фун
кциями.
П
у
с
т
ь
1 =
{Г,
2, ... ,
г
}
,
I
p
= {i
1
, .
..
, i/
p
} = 1,
т
(/
р
)
=
(i )
(i,p
)
и
) (1,1')
=
m
,
р
(
х
1 ,
...
,
Х
) , S
(/p)
=S'p(x
1. ... , X ).
Т
о
г
д
а
сп
р
а
ве
д
ливы
с
л
е
д
у
ю
щ
и е
ф
ор
м
у л
ы
Л
еонова
-Ширяева
с
в
яз
и
моментов
и
с
е
мии
нвариа
нт
ов.
q
q
т
(1
) =
~
п 5 (1
р);
5(/
) = ~ (- I)q- 1(q - 1
)1
П
m (I
p
) ,
A
q
1'=1
A
q
1'
=1
( 1.3 .2)
г
д
е
з
а
п
и
с
ь
~
...
оз
на
чает,
что
с
у
м
мирование
в
ып
о
лняется
по
A
q
в
сем
неуп
орядоче
нным
р
азби
ен
иям
A = {I = lJ1
Р
}
мн
оже
с
т
q
1'
=1
ва
1
на
множест
ва
11'
...
,
/
ц
такие
,
что
l ; n
Ij
=j=.
0,
i=f=.
i ,
q
Ul
p .-=l.
р
=l
23
22

В
частно
ст
и
,
есл
и
~
(
х)
Е
т
(
4
)
И
M
~
(х)
=
О
,
т
о
при
I =
=
{
Г
,
2. 3, 4}
»,
(
х
ll)
,
х(
2
)
,
х(
3
),
х
(4»
= 54
(х(\)
,
х(
2),
х
(
3)
,
х
(4
»
+ m
2
(x(l),
х
(2»
Х
Х
»«
(х
(3)
.
х
(
4
»
+ m
(х
(l)
.
х(
3
»
m
(х(2)
,
х(4»
+ m
(
х
(
I!,
х(4»
Х
2
2
2
Х
m
2
(
х(2)
,
х
(3
».
(1.3.3)
Р
а с
с
м
о т
ри
м
груп
пы
д
виже
ний
М
(
п
)
,
т,
SO
(
п)
,
вв
е
д
е
нн
ые
в
п
.
1. 2.
Если
~
(х
)
Е
Т
(
m
)
И
д
ля
всех
1
~
r
~
т,
т
Е
R
n
т,
(x(l),
...
,
х
(
г
»
=
Пl
,
(х(1)
+
т,
.. .•
х
(г)
+
Т
),
(1
.3.4)
т
о
скажем,
что
~
(х)
Е
S\m
).
Е
сли
для
всех
g
Е
SO
(
л),
1
~
T
~
m
вып
о
лнен
о
соо
т
но
ше
н ие
(1)
-<f
» (\)
(
г
»
1 3 5)
т
,
(
х
. ... ,
х
=
т
; (gx •... , gx , ( . .
то б
уд
е
м
п
и
с а
т
ь
~
(
х
)
Е
s
~
m
).
Вм
е
ст о
~ (х
)
Е
S\m) n
S
~
m
)
пиш
ем
~ (х
)
Е
S(m).
В
э
т
о
м
слу
чае
все
м
омен
ты
и
семи
инва
р
иа
нты
п
о
л
я
до
п
о
р я
д
к
а
т
и
н
вариа
нтн
ы
от
носитель
но
гр
упп
ы
М
(п)
.
В
силу
(1.3.2)
в
(1.3.4), (1.3.5)
вм
е
ст
о
мо
ме
нто
в
т
,
(
·
)
м
о
ж
н
о
пи
с
а
ть
сем
и
и
нва
р
иа
нт
ы
5,
(.).
Е
сли
s
(х
)
Е
т
{m
)
и
д л
я
(R
Гn
всех
1
~
r
~
т
н
а
,
)ВГn)
су
щес
т
вует
вп
о
лн
е
ко
не
ч
на
я
ко
м
пл
е
к сн
а
я
м
е
ра
F (.)
така
я,
ч
т
о
для
в
с
е
х
1
~
j
~
r
5,
(х(1),
... ,
х(
г»
= S
ех
р
{i
~
(x (j ),
л
и»)
F
(
d
л(1)
,
... ,d,
,,(
r»,
Jl.Гn
}=l
J
т
о
~
(х
)
Е
ф(
m)
.
Е
сл
и
п
о л
е ~
(х)
Е
ф
е
т
)
,
т
о
~
(х
)
Е
Sr >
то
гда
и
только
т
о
г
да,
когда
дл
я
1
~
r
~
т
il'
le
p bl
.
Р
(. )
сосредоточе
ны
н
а
п
о
дп
р о
ст
р
ан
с
т
в
е
L (
f)
(О),
о
преде
ляемо
м
у
ра
в
не
н
ием
л(l)+
...
.
..
+
л
(г
)
=
О,
т
.
е.
F
(Л)
= F
(
Л
nIY )
(О»
,
Л
Е
)В
Гn,
1
~
r ~
т
.
Б
у
дем
говорить,
ч
т о
пол
е
S
(х)
Е
з
\
т
),
если
~
(
х
)
Е
Ф
'
""
nS\m)
и
дл
я
к
а
ждо
г
о
1
~
r
~
т
мера
F
(Л).
Л
E)ВГIJ
абсо
лют
но
н
е·
пр
е
ры
вн
а
о
т
носит
ель
но
(
г
- 1)
л
-
м
ерн
о
й
м
е
ры
Лебега
н
а п
о
д
п
ростра
нс
тве
L(r)
(О).
В
этом
слу
ч
ае
су
ществуют
ф
у
н
кц
ии
[,
(1-..0)
, ... .
л(
Г»,
на
зываемые
спектр аль
ными
П
Л
ОТН
О
С
Т
Я
~
1J1
п
о
·
г
-1
р
ядка
r
~
2,
так
ие,
ч
т
о
ЛИ
= -
~
ли)
н
j=1
I I"
(Л,(
I)
,
...
,
"
(Г
»
I
dл
(l
)
.. .
dЛ,
\
I
-
I
J
<
00.
(1.3.6)
R{r -
l)n
24
Замети
м
.
что
ф
ун
кц
ии
"
(Л,(1
)
,
... , ;",(
f»
с
и
мме
т р
и
ч
н
ы
е
,
и в
о о
бщ
е
го
во ря
.
ко
м
пл
е
ксно
зна
ч
ные
.
Ф
а
к-т
ич е
с
ки
п
е
р
е
м енн
ая
л(г)
=
= -
л(l)
- ... -
л(
г
-
1)
я
в
ля
е
тс
я
символ
и
ческой
,
по
э
т
о
м
у
мы
б
у
де
м
уп
отр
е
бл
ять
е
ще
обоз
на
чен
ие
[,
(
л
(1
)
,
...
,
Л,(Г
-
l
»,
r
Е
{2, ... ,
т
}
.
Н
аиб
о
л
е е ч а
ст
о и
сп
о л
ь
з
у
е
т
с
я
с
пе
кт
ра
ль
ная
п
л
от
н
о
с
ть
в
то ро
го
п
ор
яд
к
а
[2
(л(1),
-
л(1»
=
[(л(1»
(с
м
.
(1
.2.2».
а
такж
е с
п
е
к
т
ра
л
ь
на
я
пл
о
тн
о
с
т
ь
ч е
твер т
о
г
о п
оря
д
к
а
{
4
(л(l),
л(
2)
.
,
У\
Дл
я
гау
ссовс
к
ог
о
п
ол
я все
с
пект
ра
л
ь
н
ые
п
л
отн
о
с
ти
[т
(.).
т
>
2
р
а
вн
ы
н
у
л
ю
.
Т
аки
м
об
разо
м
.
ес
л
и
s
(х
)
Е
зl
т
)
,
т
о
дл
я
все
х
r
Е
{2
,т
}
су
щест
вуют
од
но
ро
д
ные
с
пек
т
раль
н
ые
п
л отн
о
с
т
и
[;
(Л(l)
л(
Г
-1»
та
к
ие
.
ч
то
в
ып
о
л
н
ен
о
(1.3.6)
и
5 (
v (1)
Х
(Г»
= 5
(
х
(l)
_
х(
Г)
X{f-
I) -
х
(Г
)
О)
=
r
л
-
I • • • , r ,
о
••
, ,
)
ех
р
{i
Г
~
(
л
о
) .
х(})
_
Х
(
Г»
)
}
{,
(л(1)
• ••• , , ,,(f - I)
Х
R(f - l)n
;=
1
Х
dЛ,(I)
...
d
л
(Г
-I
).
(1.3.7)
'
П
р
е
д
с
т
а
в
л
е
н
и е
(1.3.7)
п
ри
r = 2
п
р
е
в
р
ащ
а
ет
с я в
(1.2.2).
И
з
в
е с
т
н
о
,
чт
о
д
л
я
п ре
д
ст
а
в
лени
я
(1
.3.7)
дос
т
ато
ч
н
о
.
н
а п р и
мер,
ч
то б
ы
I I
5
(
Г
)
(х(I)
,
..
. , X(f
-I)
,
О)
I
dX
(I) .. .
dX(f-l)
<
00
.
(1
.3.8)
JI.(f- l)n
В
слу
чае
г
а
у
с
с
ов
с
к
ог
о
п
о л
я
(1
.3.8)
о
з
н
а
ч а е
т
,
что
к
.
ф
.
п
о
л
я
аб
солют
но ин
т
е
г
р и р
у
е
м
а
.
Е
с
ли
п
оле
~
(х)
Е
ф(m)
n
S
~
n
)
,
т о
для
любого
g
Е
SO
(л),
1
~
r
~
т
F
(л(l),
... ,
Л(
Г»
= F
(gЛ(l
)
....
,gл'(Г').
(1
.3.9)
В
ч а
ст
н
о
с
т
и
,
ес
л
и
s
(х
)
Еф(т)
nS(m),
т
о со
отноше
н
ие
(1
.3.9)
вы
п о
л
н
я
е
т
с
я н
а
L (m)
(О
)
.
Д
е й
с
т
в
и т
е
л
ь н о
,
если
g
Е
SO
(
п
)
,
и
(j
)
=
- 11
и)
1
----
.
---- ----
= g " ,
"'=:::::
J
"'=:::::
r
"'=:::::
т
,
то
(
J
I)
(
г»
((1
)
И
)
S,
Х
, .. . ,
х
= 5, gx , ... , gx =
= I
е х
р
~
i
~
(ли).
gX(j»}
F
(dл{l)
,
..
..
d
л(г)
=
R'n l }
=I
= I
ехр
{i
.
~
.
(g-l
Л,(
/)
,
X
O~
}
F
(dл(l)
,
... ,
dл(
Г»
)
=
Jl.Гn
}= l
=
~
ех
р
{i
~
(
И(/)
,
х
(/
)
)
}
F (d
(
gи
(!
))
, ... , d
(
g
и(Г)
)
)
.
RГn
)=
!
25
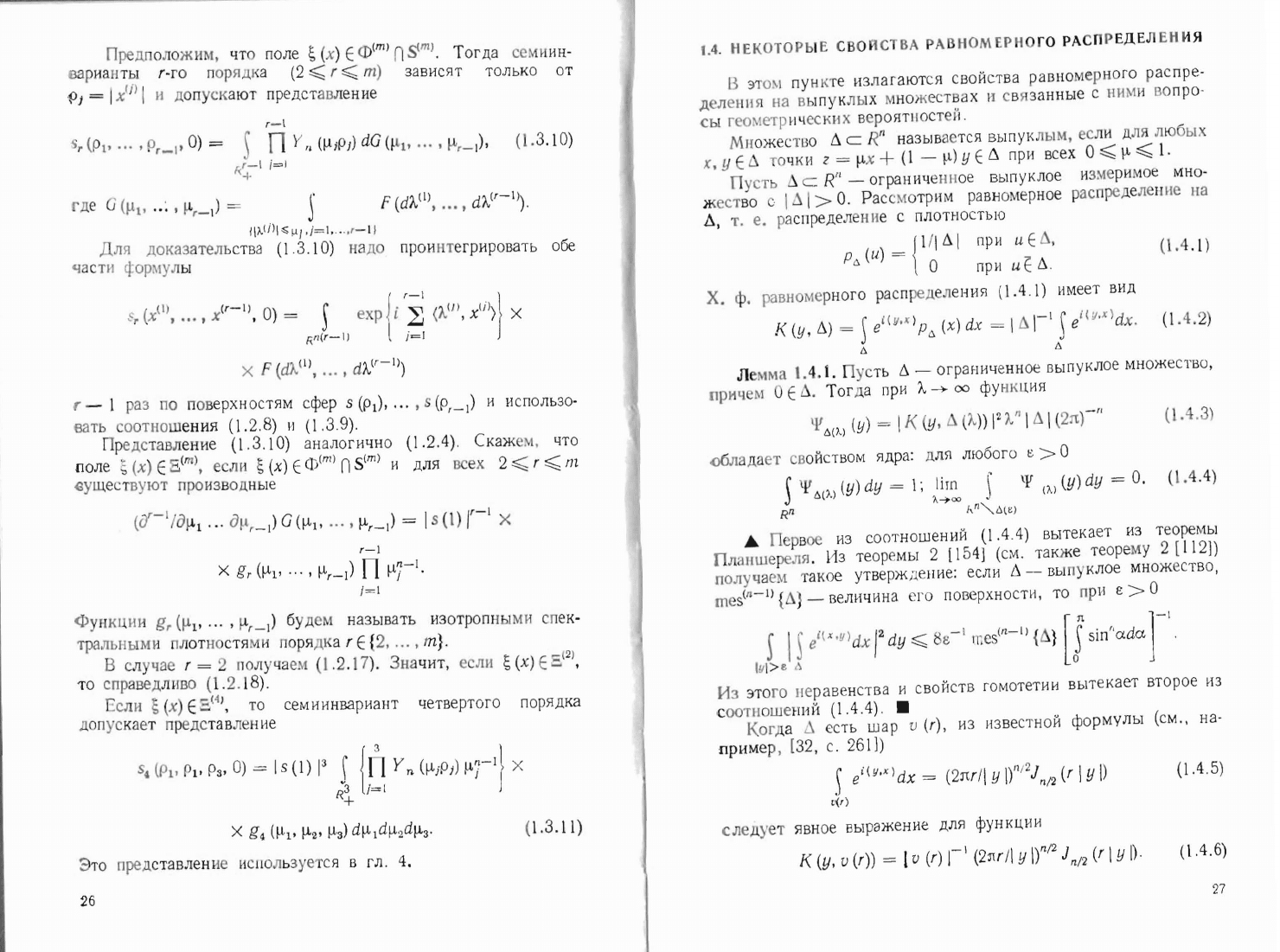
r
-l
Пре
д
п
о
л
ож
и
м,
чт
о
поле
;
(
х
)
Е
Ф
'
?"
n
s(
m).
Т
ог
да
се
м
н и
н
ва
р
и а
н т
ы
г-
г
о
п
о р
я
д
ка
(2
~
г
~
т
)
зависят
тольк
о
от
f)j = I
х'п
I
11
д
о п
ус
к
а
ю
т
пр
е
дст
а
вление
Sr
(
Р
l
'
....
р,-!,
О)
=
~
П
)
/
"
(l-1iР
J)
dG
(
~
l
l
'
... ,
~
L
,
_
l
)
'
(1.3. 10)
, r - l i=1
'(+
. l' F
d
~
(')
d
~
(r-l
)
гд
е
С
(
1-11'
...
•
~
г-
l
)
= J ( '" , ..•, '" ).
I\
/о..
(
п\
~
1-1/
./= 1.....' - 11
л
я
д
о к
а
з
а
т
е
л
ь
с
т в
а
(1
.3.1
О)
на
д
о
прои
н
т
егрирова
ть
о б
е
ч
а
ст
и
ф
о
рму
л
ы
f
г
-1
}
1i
Sr (X(IJ, •• • , X(f - I),
О)
= j
е
хр
,i
~
('л
(J
) ,
X ,)
х
;;,,(r- I) l i =1
Х
F (d/.(l), ... •
d
'л
(
г
-
l
)
)
( - 1
р а
з
п
о
п
о
верхн
о
стям
сфер
S
(р
.)
,
...
, S
(Р,
-I)
и
и
сп
оль
з
о
ват
ь
с
оо
т
н
о
ш
е
н
и я
(1.2.8) 11
(1
.3.9).
Пр
е
д
с
т а в
ление
(1.3. 10)
а
на
л
о
г
и
ч
н
о
(1.2.4).
Скаж
е
м
.
чт
о
п
о
л
е
:;
(х
)
Е
з,
(т\
есл
и
;
(х)
Е
ф
(
m
)
ns (m)
И
для
в
с
е
х
2~ r ~
т
су
щ
е с
тв
ую
т
проиэ
воц
н
ы
е
([f-l
/
д
fJ.
l
"
·
д
~!
'
_
I
)
G
(
f.L
l
'''
· '
fJ.г-l)
=
I
s
(
1)Г
1
Х
г-l
Х
е,
(f.L
l'
... ,
f.Lг
-I)
П
f.Lj-I
.
/= 1
Ф
у
нк
ци
и
gr
(fJ.
l' ... .
~
г-l)
б
у
д
е
м
на
зыв
ать
из
отр
опн
ы м
и
сп
е
к
тральным
и п
л
о т н о
с
т
ям
и
по
р
я
д
к
а
г
Е
{2, .., ,
т}
.
В
с
лу
ч
а
е
r = 2
по л
у
ч
а е
м
(1. 2.17).
З
на
ч
и т
.
е
сли
;
(
х
)
Е
=.( 2),
т
о
с
пр
а
ведл
11 13
0 (1.2.18).
Е
сл
и
;
(
х
)
Е
:=.(
4' ,
то
семиинва
риант
четве
рт ог о
п
ор
ядка
д
о
пу
с
к
а
е
т
п р
е
д
с
т
а
в
ле
н
и
е
S4
(Рl'
Pl '
Рз.
О
)
= Is (1) 13
~
{f
l
у
n
(~j
PJ)
~tГl}
Х
R3 /= 1
+
(1.3.11)
х
е,
(~
tl
'
fJ.2'
I-1з)
df.L
ld~
2d
~з·
Э
т
о
пре
д
с
т
а
в
л
е
н
ие
и
сп
о
л
ь
э
у
е
т
ся
в гл.
4.
1.4.
Н
ЕКОТ
О
Р
Ы
Е
сво
и с
т в
х
Р
АВ
н
О
М
Е
Р
НО
Г
О
рд
С
n
РЕДЕ
Л
Е
Н
ИЯ
в
эт
о
м
п у н
кте
и
зл
агают
ся
с
в
о
й
с
т
ва
р
авно
м
е
рн
ого
р
аспре
деле
пи
в
на
в
ы
п
у
к
л
ы
х
м
н
о
же
с
тва
х
11
с
в
я
з
а
н
н
ы
е
с
ним
и в
о
п р
о
с
ы
Г
С
О~
lе
тр
н
чес
!
шх
в е
РО
Я
ТI10с
т
е
i
'
l
.
Мн
о
ж
е с
тв о
~
с
Е
<'''
н а
з
ы
в
а
е
т
с
я
вып
у
к л
ы
м
,
ес
л
и
д
л
я
л
юбы
х
х,
У
Е
v.
то
ч
к
и
г
=
fJ.
x + (1 -
~t)
У
Е
~
п
ри
всех
О
~
~
~
1.
П
у
с
ть
~
с
R" -
о
г
р
а
н
и
че
н
н
ое
вып
у
клое
И
З
~
leри
м
ое
м
но
ж
е с
тв
о с
I
~
I>
О
.
Р
а
с с
м
о
т
р и
м
р
авн
ом
е
рное
ра
с
п
рсд
е
Л
С
Н
ll
е
на
д,
Т.
е.
р
а с
н
ре
д
е
.rr
е
ни
е с
п
л
отн
о ст
ью
1
/1
d.1
при
u
Е ь.
(1
.4.1)
Р
()
и
=
с.
{
О
приu
td.
.
Х
.
ф, ра
в
н
о
м
е
р
н о
г
о
р
а
сп
р е
д
e.r
Jения
(1.4. 1)
имеет
вид
К
(у,
d.)
=
~
ei(Y.X)
Рс.
(
х)
dx = I
d.
г
~
ei(!I,X)dx.
(1
.4.2)
'
t; t;
Л
е
м
м
а
t.4. 1.
П
ус
т
ь
d.
-
о
гра
н и
че
н
н
ое
вып
укл
ое
мн
ож
е
ств
о,
пр ичем
О
Е
v.
.
Т
ог
д
а
п
р
и
')."
-
)о-
00
Ф
У
Нl
щи
я
1
1'
t;
Щ
(у
)
= \
К
(
у.
L\
(1.)
) 12
')."
n \
d.
\
(
2
пГ
"
(1.4 .3)
осл
а
л
ает
СВ
О
Й
С
Т
В
О
М
я
д
ра:
дл
я
л
ю
б
ог
о
е
>
О
r
1.1
' t;(/.)
(у
)
dy = 1; lirn
('
ч
r
(/о..)
(у)
dy =
О
.
(1.4.4)
J 1\-.+00 J
R
n
/,
n
".с.
\
е)
•
Пер
в
ое
и
з
с
о
о
тношений
(1.4 .4)
вытека
ет из
т
еоремы
П
лзнше
ре
ля
.
И
з
те
о
р
емы
2 [ 154]
(
см.
т
ак
же
т
е
оре
м
у
2 [ 112])
получ
аем
т
ак
о
е у т
вер
ж
де
н и
е
:
если
v.
-
вы
п
уклое
множ
е
ство,
mes
(n
- l)
{
~}
_
вели
чин
а е
г
о
п
ов
ерхн
о
сти
,
т
о
п
р
и
е
>
О
n
]-
1
~
\
~
ei(x
'Y)
dx
12
dy
~
8е
-
1
п
;
е
s(
n
-
I )
{
~}
~
s
i
п
"
а
d
а
[
1
1I
1>e ,\
О
Из
эт
о
г
о
пе
р а
в е
н
с
т в
а
и
с
во
й
с
тв
г
о
м
о
т
е
т
и и
выт
ек
ает
вт
о
р
ое
нз
с
оо
т
н
о
ш
ен
ий
(1.4.4) . •
Когд
а
L\
ес
т ь
ш
а
р
v
(г)
,
и з и з
ве ст н о
й
ф ормулы
(
см
..
на
п
р и
м
е
р
,
[32,
с
.
261])
.\
/
(
у
,
х
)
dx =
(
2пг
/\
у
1)'
1/2J"/2 (r \
у
\)
(1
.4.5)
t(г
)
сле ду
е
т
явн
ое
в
ыра
ж
е
н
и
е
для
функции
(1.4.6)
К
(у,
v
(
г
) )
= 1v
(г)
г\
(2J1
r
/1
у
\)11
/2 J
11
/2
(
г
I
у
[).
27
26

Есл
и
6 =
П
lа
.
Ь)
,
то,
очевидно
,
fI
К
(у,
11
/
а
,
Ь»
= n
(i
bi!l, -
е' Й
i
!!
j )
/
[i
у
) (
Ь
]
- aj)]'
(1.4.7)
;= 1
Соотнош
е
н
ия
(1
.4.4)
для
функ
ц
и и
Ч'
V
(Г
)
(у)
в
ытекаю
т
113
(1.4.6).
В
самом
деле,
п
ри
л
ю
б
о
м
е
>
О
,
r
---+
00
J
I
К
(
у
,
v
(г
»/
2Г
"
(
2
пГ
"I
V
(I
)ld
у
=
;;
"
".
Со'(
е
)
00
=
2Г
(
п
/2
+
1)
г-
1
(п/2)
I
J
~
12
(
11-)
~t-
l
dl1-
->
О
.
ГЕ
Е
с
ли
6
=
П(Ь)
,
т
о
из
(1.4. 7)
ЧJ
щ
ь
)
(
У
)
=
(
2
п
Г
"
I
П
(
Ь
)
l l
х
"
х
]
К
(у
,
П
(Ь
»)
12 = n
ФЬi
(Уl
)
'
г
д
е
ф
т(
z
)
= sin
2
{z
T/
2}/{
2J1
T
х
/=1
Х
(г/2
)2}
-
ядро
Ф
е
й
е
р
а
.
В
ЭТО
м
с
л
уч
ае
такж
е
в
етру
дно
вы
вес
ти
с
в
ойст
в
а
я
д
ра
'Р'П
l
Ь
)
(У
)
ти
па
(1.4.4)
или
miп{Ь
j
,
i = 1, ... ,
п}
---+
00
.
в
да
льнейше
м
в а
жн
у
ю
ро
л
ь
игр
а
ет
ф,
р.
Р
(z) = F
(г)
А
" PaS
рассто
я
ния
Р
= I
а
-
~
I
м
е
ж
д
у н
е
з
ави
симыми
случайными
С
Ф
т
о
ч
к
ам
и
а
и
~,
в
ыбра
н
ными
п о р
авном
ерному
закону
во
мн
о
ж
е с т в е
6.
О
б о
з
н
а
ч и
м
неполную
бета
-фу
нкцию
х
I
'
х
(р
,
Q)
=
г
(р
+ q)
г-
1
(р)
г
-
(q) Jt
P
-
1
(1 -
t)Q
- l
dt
,
о
р>О,
Q>O
,
х
Е
[О,
I]
.
(1.4. 8)
Л
е
м
м
а
1.4.2 169,
с.
64].
П
л
о
т
н о
с
т
ь
р
а
спр
е
д
е
л
е
н
и
я
'Фг
(
и
)
р
а
сс
т
оя
н
и
я
между
д
в
ум
я
н е
з
а
в
и
с
имы
ми
и
р
а
вн
о
м
ер н
о
р
а
с
преде
л
енными
т
оч
к
а
ми
вн у
тр
и
ш
ар
а
v
(
г)
'1
'
г
(u)=ПU
,,
-I
,-
П'
I_
U
'
/
(
4f
'
)
«П
+
1)/2,1 /2),
О :(;и :(;2
г
.
(1
.4.9)
З
а
м
е ч
а
н
и
е
1.4 .1.
Пр
и
п=
1, 2, 3
соо
т
но
шение
(1.4.9)
дает
соотве
т
с
тве
н
но
т
а
к и
е
выражения:
(1 -
и
/(2г
»
/г,
8
{
и
/
(
2г
)
}
х
х
[arccos
{
и
/
(
2
г)
}
-
{
и
/
(
2г
)}
V 1 -
(и/(2
г»2
]/(
nr),
6
(
и
/(
2г
)
2
х
Х
(1 -
и/(2г»
2
(2 +
u
/(2
г»
/
г.
Лемма
1.4.3.
Пусть
v
(
г
1
)
и
V
(
г
2
)
-
два
ко
н
це
н
т
р
и
ческих
шара
в
Rn(r} < (
2
) ,
а
а
-
с
л у
ч
а
й
н
а
я
т
оч
к
а
в
перв
о
м
ш
аре
,
выбранная
п
о
ра
в
но
мерному
закону
,
~
-
н
е
з а
ви
сим
а я
о т
а
28
с
лу
чай
ная
то
чка,
выбра
нная
п
о
ра
вноме
р н
о
му
закону
BHY
~
ри
ша
ра
v
(
г
2
)
.
Т
ог
д
а п
л
от
н
о
сть
р
а
с
пр
е
д
е
л
е
ни
я р
а
с
ст
оян
и я
Paf3
ме
ж
ду
этим
и
т
оч
к
а
м
и
име
е
т
ви
д
ЧJ
(
и)
=
2(п-2)
!2
г
(
п
/2)
n
2
11
"/2
(
г г
.
)"/2
Х
(t
o' " 1 2.
00
х
.~
р-
"
/
2J
(
,,_
2
)
/2
(U
р
)
J
nI2
(f1
Р
)J
' 1
12
(f
2
Р
)
dp,
uЕ
[0
,
г
1
+
г
2
1
·
(1.4.10)
о
Ле
м ма
1.4.3
может бы
ть
доказа
на
метод
ом
х
.
ф,
От
м
етим
лиш
ь,
ч т
о
при
Г
1
=
Г
2
=
Г
(1.4.10)
превращается
в
(1.4.9).
Л
емма
1.4.4.
П
у
ст
ь
s
(
г)
-
сфера
в
Р",
п
> 2.
Ес ли
а
и ~
независимые
слу
чайные
то
чки
,
выбранны
е
на
s
(
г)
п
о
равно
мерному
закону,
т.
е
.
Р
{а
Е
6} =
Р
{
~ E
6} =
.~
dm
(х)/
t. n S(rJ
/[r"- I Is (1) 1
1,
6
с
s
(
г),
т
о
п
л
отн
о
ст
ь
рас
пределения
расс
тоя
н
и
я
P
a S
между
то
чками
а
и
~
fr
(
и)
=
n
-
1
/
2
г
(
п/2)
г-
1
«/1
- 1)/2)
г
1-
"
и
а
-
2
Х
Х
(1 -
u
'2
/
(
2г
)
2
)
(
Гl
-
~
)
j2
,
0<
и
<
э
(1.4.11)
Лемма
1.4.5.
П
у
ст
ь
s
(
г
1)
и
s
(
г
2
)
-
д
ве
ко н
це
и три
чес
ки
е
сферы
в
R",
п
>
2
с
ра
диуса
ми
Г
1
11
Г
2
(
Г
1
«
2
) ,
а
и
~-
H
e
зависимы
е
р
а в
н
ом
е
рн
о
р а
сп
р
е
д
е
л
е н
ны
е
н
а
каждой
из
н
их
Т
О
Ч К
И
.
ТО
Г
д
а
пл
о
т
н
о
ст
ь
рас
преде
ления
расстояния
РаВ
м
е
ж
д
у
эт
и
м
и
то
чк
а
м
и
равна
О
при
U< r
2
- f
1
•
U>
Г
1
+г
2;
f
(
и)
при
"1'Р
?
и
Е
[
Г
2
-
г1' Г
1
+
г
2
1
,
г
д
е
л;
-
lJ2
г
(п
/2
)
г
' f
(ц)
=
«(
п
- 1)/2) 23- "
(
г г
)2
-
11
Х
' I
,'
s 1 2
Х
((Г
+ ()2-
u
2
J(П
-
3)!2
[
IР
-(
г
-
(
2
)
'2
I
(
П
-
З
)
!2.
(1.4.12)
1
2
1
Д
о к
а з а
те
л
ь
с
т
в
о
лемм
1.4.4
и
1.4.5
осн
ова
но
н
а
геометри
чес
ких
вероятн
остях
.
О
с
т
а
н о
в
и
м
с
я
ли
шь
на
доказательстве
лем
м
ы
1.4.5.
...
Б
у
дем
с ч
итать,
что
од
на
из
то
чек
а
или
~
ф
иксирова
на
и
сов
падает,
н
а
п
ри
м
е
р,
с
«се
ве
рны
м
п
о
л
ю
с
ом
»
бо
ль
шой
сфе
ры,
Г
2
-
Г
1
<
и
<
Г
2
+
fi
.
Если
п
ер
е
й т
и к
сферической
с
и
с
теме
коорд
и
нат
(1
.1.1),
т
о
в
ероя
тность
слу
чайно
го
событ
ия
{
Ра
В
<
и}
ест ь
от
но
ше
н
ие
пл
ощ
а
ди
п
о
в
ер
хн о
с
ти
се
г
ме
нта
2
{(
<р
,
<Р
1
'
... ,
<р
n- 2) I
О
:(;
<Р
1
:(;
А
}
,
г
де
А
= arccos
{
(г
~
+
г
~
- u
)/
'l(2
r
) } ,
которая
рав
на 2
n(n-
IJ
!2
г\n
-')
!2
Г
-
]
«n - 1)/2)
х
1
f
2
А
Х
) sin"- 2
<P
1
d<P
l'
к
п
л
ощади
пов
е
р
хн
о
с
т
и
сфе
ры
s
(
г
1)'
е
л
е
о
29

до
вател
ь
н о
,
А
P {P
t;C
'j <
и}
=
л
-
1
nГ
(
/1
/2 )
г
-
I
((
/1
- 1)/2) \ sin
n
-
2
<r
]((cp).
d
О
т
с
ю
д
а
в
ы
т
е
кае
т
(1.4. 12).
М
н
о
г
и
е
ф
а
кт
ы
,
п о
л
уче
н н
ые д
а
л
е е
с
и
с
п
ол
ь
зов
а
н и е
м
лемм
1.4.2
-]
.4.5,
м
о
гу
т
быть
об
об
щ
е
н
ы
н а
сл
у
ч
а
й
д
р
угих
м
н
о
ж
ес
тв
6,
д л
я
к
о т
о
р
ы
х
и
зв
ест н
а
ф
.
р.
F
t>
(
г
)
.
Н
а
п
р
и
м
е
р
,
п
ри
п
= 2
м
о
ж
н
о
и
с
п
о
л
ь
з
о
ва т
ь
сле
ду
ю
щ
е
е у т в е
р
ж
д
е
и
и
е
,
к
о
то
ро
е
м
ожно
л
ок
а
з
а г ь
с
п
о
м
о
щ
ь
ю
гео
ме
т р и
ч е
с
к
их
в е
ро
я
т
нос
т
е
й
и
л
и
н
споср
е
л
с
тв
е
и
н
ы
м
и
нт
е
г
р
иро
в а
н
ие
м
.
Лемма
1.4.6
[42].
Пу
с
ть
!J.
=
[
О,
а
1
х
[
О
,
а
]
с
R2-
ква
д
р
а
т
.
Т
о
г
д
а
ф
у
н к
ц
и я
р
а
с
пр
е
д
е
л
е н
и
я
Р
{).
(и)
р
а с
с
то
я н и
я
P
~
м
ежду
н
еза
в и
с
и
м
ы
ми
с
л
у
ч
а
й
н
ы
м
и
то
ч
кам
и
а.
11 [1,
вы
б
р
а
н
н
ы
м
и
в
!J.
по
р
авном
ер
н о
м
у
з
а
ко
н у
,
рав
н
а
О
п
ри и
~
О;
11
(
и
)
п
р
и
О
<
и
~
a
;
f
2
(
и
)
п
р
и
а
<
и
~
а
V
2;
1
п
р
и
и
:»
а
J/'2,
г
д
е
f)
(
и)
=
n
и
2
/
а
2
-
8и
3
/
(
3а
3
)
+ u
"
/(20
11
) ,
[2
(и)
= 1/3
-+
4 J!
ц
2
-
а
2
/
/
а
- (2 +
п)
ц
2
/
а
+
4
ц
2
arcsin
{
а
/
и
}
/
u
2
+ 8 (
11
2 -
(2
)
З
/ 2
/
(3
а
~
)
+
+
II~/(
2
a
' ).
1.5. ДИСПЕРСИИ
ИНТЕГРАЛОВ
ОТ
СЛУЧАйНЫХ
ПОЛЕЙ
И
с
с
л
е
д
у
е
м
а
с и
м
п
то
т
и
ч е
ск
ое
п
о
в
е
дение
д
и с
п
е
р
с
ий
и
н т
е
г
р
а
л о
в
о
т
с
л
у
ч а
й н
ы
х
по
лей
в
корр
е
л
я
цио
нны
х и
с
п
е
кт
р
а
ль
н
ы
х
т
ер
м
и
на
х
.
П
усть
!J.
().) -
г
о
м
от
ет и
ческ
и
й о б р
а
з
о
г
р
а
н
и
ч
е
н
н
ог
о
изме
ри
м
о
го
в
ып
у
к
л
о
г
о
мн
о
ж
е
ст
в
а
!J.
с
I
!J.
I > 0,
со
держащ
ег
о
н
а
чал
о
коо
р
д
и нат, ~
:
Q
х
Р
"
--
R
1
-
с.
к
,
н
е
прерывн
ое
из
м
е
р
и
м
ое
о
д
но ро
д
н
о
е
из
о
тр о
пн
о
е с
л
у
ча
й
но
е
п
о л
е
с
M~
(х
)
=
О
.
О
б
о
з
н
а
ч
и
м
у]
(
л
)
= \
~
(
х
)
dx.
Н
а
ос
н
ов
ани
и
ра
н
д
о
м
и
з а
ци
и к
.
ф
,
6(;.)
в
обо
з
н
аче
н
иях
п
.
1.4
ь
(л
)
=
D1]
(л
)
=
~
J
в
(1
х
-
у
1) dxdy = I
!J.
(
л
)
12
М
В
(Paf\) =
6 (1.)
t>Ш
d
( л.
.
2
= I
!J.1
2
,.
',
J
В
(г
)
dF
t>
<ЛJ
(
г
)
,
(1
.5. 1)
где
P
a
~
-
ра
с
с
т
о
я
н
ие
ме
ж
д
у н
еза
вис
и
м
ы
мв
точк
а
м
и
а
и
~,
вы
бр
ан
н
ы
ми
п
о
ра
в н
о
м
ерн о
м
у
за
к о
ну
во
мн
о
ж
е
с
т
ве
!J.
(1.
),
d
(
л.
)
-
диам
етр
м
н
ож
е с
т
ва
!J.
(
л
)
.
И
сп
ольз
у
я
(1.4.9),
д
л
я
шаров
v
(г
)
с
R"
и
з
(1.5.1)
п
о
лу
30
ч
а
ем
ь
(
,)
= D l J
~
(х)
ах
1=
t(,)
2,
=
С
2
(
п
)
, n
~
zn-
1
8
(г
)
I
l-
z' /(
'2.r
l'
«(11
+ 1)/2 ,1
/2)
dz,
(].5.2)
n
г
д
е
С
2
(
п
)
=
4
n"
n
-
l
г -~
(
п
/
2
)
,
(1.5.3}
а
I
х
(р
,
q)
о
п
ре
д
ел
я е
т
с
я п о
(1.4.8).
А
с
и
мп
го
т
и ч
е
с
к
и
й а
на
л из
ф
о р
м
у
л
ы
(1
.5.2)
п
оз
в
о л
я е
т
сф
ор
м
у
лир
ова
т ь
с
л
е
д
у
ю
щ
е е п
р
е
д
л
о
ж
е
н
и
е.
Лем
ма
1.5.1.
Е
с
л
и
эс
00
~
<,,,
-1
I
в
(
г
)
Idz <
00
, 1\ = J
г
n-
I
В
(
г
)
dz
=1=
О
,
(1
.5.4)
о
т о
при
г
--
00
Ь
(г)
=
С
2
(л)
(
1
)
Г
"
(1 + 0
(1
»).
А
н
а
ло
г
и ч
но
,
исп
о
ль
з
уя
(1.4.1
О)
,
п р и
'1
<
Г
2
нах
одим
М
J
~
(
х)
dx J
q,
(
у
)
dy = J )
в
(1
х
-
у
1) dxdy =
u(
, ,' 1,(
',
) ''( ' , ) u(', J
',+1,
=
(
Г
1
Г
2
(
I
V
(
I
)
12
М
В
(
Ра
~
)
=С
з
(
П
)(
Г
1
Г2
)n
l2
J
B(r
)r'
l/'2
x
х
lj
р
-
n
n
) (n
-2
)
12
(
г
р)
)
n
п
(
г
)р)
Jn
12
(
г
2
Р
)
о
dp ] dr ,
n
г
-
1
г
де
C~
(
п)
=
2
"
/
2
n
(п
/2),
а
p
~
-
расс
т
о
ян
ие
м
е
ж
д
у
не
з
а
в
и
си
мыми
сл
у ч
а
й
н
ы
м
и
то
чкам
и
а.
и
В,
в
ы
б
р
а
н
ны
м
и
п
о
р
авн
о
м
е
р н
ом
у
з
а
к
о
н
у
в
v
(г
1)
и
V
(г
2)
с
о о
т
вет
ст
ве
нн
о
.
И
з
п о
сл
е
д
н
е г
о
с
о
отн
оше
ни
я
,
а
т
акж
е
из
(1
.5.2)
с
л
е
д
у е т
"+',
ь
(
г
l ' ( 2) = D J
~
(
х)
dx =
С
2
(п)
)'
г
,,
-
I
В
(г
)
Х
l
]
"
~
\x1
<'
Х
{J
У
n
(гр)
,г
1
(2
)
,,12
(
г
2
р
)
- ,?
12
J
'1
/2
(г
tp)]
P
-
1
d
Р
}
аг
.
(1.5.5)
И
с
п
о
л
ь
з
уя
соот
но
ш
е
н
ие
6.571. J
[38],
м
о
жн
о
до ка
з
а
т
ь
,
ч
т
о
00
j
л
-
,,
- 1
[(
л
г
J
'
I/
~
)n/2
(лг
2
)
-
lлг
1)
11
12 J
11/
2
(
л
г
1)]'
2.
dл
=
["
J-
r?J
!n .
о
(1.5.6)
31

Ф
у
н
к
ци
я
У
n
(
г)
я
в
л
я
е
т
с я
н
епреры вной
и
I
У
n
(г)
I
~
1.
П
о
э
т о
м
у
и
з
(1.5.5),
(1
.5.6)
с
л
е
д
у
е
т
такое
ут
в
е
р
ж
д
е
н
и
е
.
Ле
м
м
а
1.5.2.
В
у
с
л
о в и я
х
(1,5.4)
при
'
1+
'
2-+00
вер
на
а
с
и
м
п т
от
и
ч е с
к
а
я
ф
о
рмула
Ь
(г
l'
(
2
) =
С
2
(n)
(г~
- (7) (1 + 0(1» .
Ан
а
л
о
г
и
ч
н о
из
(1
.4.11)
при
n>2
полу
чаем
пред
ставление
1
(
г
)
= D
[
~
~
(х)
dm
(
х)1
=
S(
r1
=
С
4
(n) ,
n
-
1
2г
) zn
-2
(1
-
z
2
/(2г)2)
(n~
З)
/
2
В
(г)
а
г
,
(1.5.7)
о
г
д
е
С
4
(n) =
4n
n
-
I
/2/
[r
(n/2)
Г
«n - 1)/2)] = 2
nn
n
-
1
/(n -
2)1
(1
.5.8)
Из
у
ч
е
н
ие
аси
м
птот
иче
ского
поведени
я
и
н
т
ег
р
ал
а
(1.5.7)
п
р и
в
од
и
т
1<
ут
в
е
р
ж
де
н
и
ю
,
аналогичному
л
е
м
м
е
1.5.1.
Л
е
м
м
а
1.5 .3.
П
у
ст
ь
n>
2,
пр
ичем
00 00
Jzn- 2\
В
(
г
)
I
аг
<
00,
~2
=
~
г
,,-
2
В
(г)
dz
=1=
О
.
(1.5.9)
о
()
То
г
д
а
пр
и
r =+ 00 1
(
г
)
=
С
4
(n)
~ 2гn-
1
(1 + 0 (
1»
.
Ч
т
об
ы
с
ф
о
р
м
у
л и
р
о
в а
т
ь
п о
д
о
б
н
ы
е
у
т в
е
р
ж
д
е
н
ия
в
с
пектра
л
ь
Н
ЫХ
те
рми
н
а
х
.
п
р
и
в е
дем
о
д
н
о
простое
у
т в е р
ж
д
е
н
и
е
тау6еро
во
г
о
ти
п
а
дл
я
и
н т
еграла
00
s
(
г)
=
~
к
(
лг)
I/
J.
g
(л)
о:
о
Л
е
м
ма
1.5.4 .
П
ре
д
п
о
л
о
ж
и
м
,
что:
а)
фу
нкция
g
(л)
непре
р
ы
в
н
а
в
нек
о
г
о
р
о
й
о к
р
ес
т
н о
с
т
и н
у л
я
,
g
(
О)
=1=
О
и
g
(л)
о
г
р
а
00 00
н
и
ч
ен
а
н
а
[0, 00);
б
)
J
к
(г)
z
r:J.d
z =
'У
(
а
)
,
JI
К
(
г)
I
z
ГA
dz
=
= l'
(
а
)
<00
.
Т
о
г
да
при
г
- »-
00
S (r) = , -r:J.-l
g
(
О)
'У
(а)
(1 + 0 (1».
.&
З
а
ме
тим, чт
о
00
f
к
(л
г)
Лr:J.
g
(л)
dл
=
,-
r:J.
-
1
'У
(а)
.
Выберем
о
В
(
г
)
"+
О
та
к,
ч
тобы
г~
(
г)
-)-
00
пр
и
г
=+
00
.
Запиш
ем
тож
де
ств
о
S
(
г)
=
,-
a.
- l
g
(
О
)
'У
(а)
+ t
(
г
)
,
где
t
(
г)
=
00
S 1<
(I,
г)
х
о
х
[g
( л. )
- g
(О
)
]
"л
(l
d Л
.
П
о
к
аж
е
м,
ч
то
п
ри
ус
л
о
в
ия
х
а),
б
)
и
32
г
-+
00 f
(
г)
=
о
(
г-
а
-
\
Д
ейст
в
ит
е
льн
о,
В
(Г)
00
If
(
г)
I
~
j' 1
к
(л
г)
11 g
(л)
- g
(О)
I
л
а
d
л
+ .) I
к
(л
г)
I
Х
о
6
И
Х
1 g
(л)
- g
(
О)
I
лОdл
~
гп
ах
1 g
(Л)
- g
(О)
I
~
(а)
г
-
а
-
I
+
О
~
)
.
~
iI
(
r)
00
+ 2
эцр
18;
(1
,) I
,-
а
-
1
\. I
К
(г
)
I zOdz.
O
~)
.
<
OO
г~
(
г;
След
овательн
о
,
f
(г)
=
0(,-
0-1) . •
Е
сли
~
(х),
х
Е
R
n
-
однородн
ое
с
л
у
ч
а
й
ное
п
о л
е
с
M~
(
х)
=0,
т
о
и
з
(1
.2.1)
и
(1.4.5)
п
олучаем
Ь
(г)
= D [ ,\
~
(
х)
а
х
i =
(2
п
г)
п
~
J
~
/2
(1
х
г
)
1
л
г
п
F
(
dл)
,
(1
.5
.1
О
)
с'
(
г)
I RrI
г
д
е
F (.)
взята
из
(1
.2. 1).
Бсли,
кроме
то
го
,
п
о
л
е и
эотропно,
то
00
ь
(
г)
=
(2nУ
г
2
п
~
J
~
/
2
(лг)
(л
гГn
С
(
dл)
,
(1.5.11)
о
г
д
е
С
(.)
в
зята
из
(1
.2.4).
Ан
а
л о
ги
ч
н
о
,
и с
п
о
ль
з
у
я
([.2 .1)
и
(1.2.8),
полу
чим
п
р
и
n
>2
00
1
(
г)
=
(2n)n/
(n
-l
)
~
Л
п
-
2
)
/2
(лг)
(л
г)
2
-
n
с
(d/..)
.
(1.5.12)
О
Вв
е
д
е
м
од
но
предпо
л
ожение
.
1.
С
п
е
к т
ра
л
ь
н
а
я
функция
С
(л),
л
Е
R+
с.
к
.
непр
ерывн
ого
однородн
ого
и
зотропного поля
аб
с
олют
н
о
н
е
п р е
р
ы
вн
а
,
п р
и
ч е
м
С'
(л)
=
!s(l)lл
CLg(Л),
aE
(- I , n),
(1
.5. 13)
г
д
е
g
(л)
-
непрерывна
я
функци
я
в
не
ко
то ро
й
окр
е
стн
о
ст
и
н
ул
я
,
g
(
О)
=1=
О
и
g
(л)
о
г
ра
ни
ч
е
на
на
[
О
,
00).
Л
емма
1.5. 5.
П
у
с
т
ь
выполнен
о
1
и
г
-+
00.
Т
о
г
д
а
а
ь
(г)
= (2n)n Is
(1)
I
С
5
(n.
а)
g
(О)
г
2
п
-
-
:
(1
+ 0 ( 1) , (1.5 . 14)
где
С
5
(n,
а)
=
Г
(n -
а)
Г
«(а
+ 1
)
/2)
/
[2
п
-
аГ
2
«n -
а
+ 1)/2)
х
х
Г
«
(
2
n
-а
+
1)/2)].
Если
в
усл
о
вии
I a E( -
I,n
-2)
,
то
при
,
-+
00
2,
а)
г
2 n
а
З
1
(г)
= (2n)n g
(О)
Is
(1)1
С
5
(n -
-
-
(1
+ 0
(1
)). (1.5
.1
5)
з
- 6·110
33

~
П
о
д
ста
в
и
м
(1.5.13)
в
(1.5.11)
и
п
ол
ожи
м
в
лем
м
е
1.5.4
К
(г)
=
J
~
12
(2)
«:"
,
И
сп
ол
ьз
уя
соо
т
но
ш
е н
и
е
6.574.2 [3
8J
:
00
~
Jv(
at
)JIJ.
(
at)
Г
Л
dt
=
а
л
-
1
г
(
л)
Г
((
'\1
+
f.L-
л+
1)/2)
х
о
х
[
2
1
Т
((~L
- V+ ),+ 1)/2)
Г
((v +
f.L
+
л
+ 1)/2)
х
х
Г
(('\
' -
f.L
+
л
+ ]
)
/2
)Г!,
а>
О,
Re (v +
~L
+ 1)>
>
Rе
л>О
,
(1.5.16)
00
при
- 1<
а
< n
за
пи
шем
\
к
(г
)
za.
dz =
С
5
(п
,
а).
Т
о
г
д
а
о
(1.5.14)
с
ледуе
т и
з
ле
м
мы
1.5.4.
Аналогичн
о
,
подс
т
а
ви
в
(1.5.13)
в
(1.5.1 2)
и
вы
б
р
ав
в
ле
м
ме
1.5.4
К
(г)
=
Лu-
2)
/2
(z)i -"
п
ри
п
>
2
п р
ий
д
ем
к
(1.5.15).
П
р
и
так
ом
выборе
K(z
)
для
00
сх
о
д
им
о
сти
ин
т
егр
ал
а
~
К
(2)
za.
dz
н
ад
о
предполаг
ать
,
ч
то
n
а
Е
(- 1,
п
- 2). •
Лемма
1.5.6.
Есл
и
в
ы
п
олн
ен
о
1
при
а
=
п
- 1
и
г
1 +
+Г2
~
00,
т
о
b
(fl'f
2)
=D
[ \
~(Х
)
dх1
=С6(
П)(
f
~-
f~)Х
'.
<;;
Ix\< "
х(1
+0(
1)),
где
с
6(п)
=
Is (I )
I·(
2n)n
g(
0)l n.
~
Ут
в
е
рж
д
ени
е
ле
м
м
ы
вы
т
ек
а
ет
и
з
пре
д
став
л
ени
я
00
ь
(
г
l '
г
2
)
= (2n)"
~
л
-
2
"
[(I,r
2
),,/2
J,,/ 2
(
лг
2
)
о
- (/
,'
1)n/2 J,,/2
(лг
1)]2
о
(dл)
с
и сп
ол
ь
з
о
вани
е
м
(1,5.6). •
З
а
м
е ч
а
ни
е
1.5.1.
Jv\
ожн
о
и сс
л
едов
а
ть
(1.5.1)
при
п
= 2
и
в
сл
уч
а
е,
ко
гда
f:, -
к
в
а
д
р
а
т.
П
р и
эт
ом
ко
н
с
тан
т
ы
ме
няю
тся
,
н о
их
мо
ж
но
най
т
и
с
и
сп
ол
ьз
овани
ем
л
е
м
мы
1.4.6.
Е
с
л
и ~
(
х)
,
х
Е
R"
-
о
д но
род
ное
с
лу
ча
й
ное
п
ол
е,
П
=
П
[
а
,
Ь
)
-
пара
л
леле
пи
пел
,
п р
ич
ем
I
п
I
~
00
,
и
(1
.5.17)
~
I
В
(х
)
Idx <
00,
Вз
=
~
В
(
х
)
dx
=?
О,
R" R"
т
о
нетру
дн
о
п
ок
аз
атъ,
чт
о
D
[А
~
(х)
dx}
=
~з
l
п
1(1 +
0(1))
.
34
Есл
и
у
п о
ля
~
(
х
)
су
щес
твует
н
еп
ре
р
ывн
а
я
и
о
граниче
нная
с
пек
траль
на
я
пло
тн
ос
ть
f
(л)
: t
(
О)
=1=
О
(
н
априме
р,
с
у
щ
е
с
т в
о
вание
,
не
прерыв
н
ос
т
ь
и
о
г
р
а
н
и
ч
е
н
н о
с
т
ь
следу
е
т
из
(1.5. J7)),
т
о
п
р
и
I
п
I
~
00
D
А
~
(х)
d
x]
=
(
2
л
)п
f
(О)
I
п
1(1
+ 0(1 )).I
Зам
еча
ние
1.5.2.
М
о
ж
н
о
п
ок
а
з а
т
ь
,
ч
то
е
сли
для
любо
го
п
ар
алл
елеп
ип еда
П
=
п
[
а,
Ь)
при
I
п
1
-+
00
D
[J
~
(х)
dx]
:::::::
I
п
1,
то
D [1
~
(
х)
dx]
:::::::
I
D,
1)
при
"
D,
':::.;:.
'
00
.
1.6.
УСЛОВИЯ
СЛАБОй
ЗАВИСИМОСТИ
СЛУЧАИНЫХ
ПОЛЕЙ
в
этом
п
ун
кте
о
п
ределяю
т
ся
условия
перс
мешив
а
ния
для
сл
уч
айны
х
п
олей
,
а
так
же
пр
и
в
о
д
я
т
с я
о
ц
е
н
к
и
ко
ва
р
иа
ц
и
и
ч е
р
е
з
к
оэ
ффи
ци
ент
п
ер
е
м
е
ши
в
ан
ия
.
Н
ап
о
м
н и
м,
чт
о
с
.
в
.
YJ
н
а
зы
в
а
ет
с
я
услов
ным
матемаги
чес
к
им
ож
и
да
н ие
м
с.
в
.
~
о т
нос
и
т
ельно
о-ал
геб
ры
U;o
c
~
,
е с
ли
:
1) 11
~
о
-и
змерима,
2)
для
всех
А
Е
~o
~
~
(ы
)
Р
(dw)=
А
=
~
ч
((
1»
Р
(dw).
А
Усло
вное
м
атем атич
е
с
к о
е
ожи
да
н
ие
с.
в
.
~
о
т н
ос
ител
ь
но
~o
обо
з
на
чается
М
(
~
/~
o
)
и
в
с
ег
д
а
су
ще
ствует
,
если
М
I
~
1<
00.
О
тм
ет
и
м
следую
щие
с
во
йс
т
в
а
условных
ма
тем
ати
че
ских
ож
и
да
н
и
й:
1)
М
(~
~/
~o)
=
~
M
(~
/
~
o
),
есл
и
M
~
~
су
щест
вует
и ~
~о
,
изме
ри
ма
;
2)
M~
=
ММ
(
~
/~o)
'
е
сл
и
М
1
~
I<
00
.
П
у
сть
9l
1
,
~
2
-
а
-алге
бры
из
~
,
а
(
~1
'
~2
)
= sup {I
Р
(А
В
)
-
Р
(А)
Р
(В)
1,
А
Е
9'1'
В
Е
9
с
2
}
-
ро
зе
нб
латтовс
к
и й
коэфф
и
ци
ент
св
яз
и
,
СОУ
(
~1'
;2) =
M
~1
~
2
-
M
~IM
1;
2'
11
~
11
" =
=
{MI
~I
P}I
/P,
р
:» 1.
Лемма
1.6.1 [28].
Е
сл
и ~
1'
~
2
-
к
о
м
п
л
е
к
сн
ы
е с
.
в
.
,
изме
рим
ы
е
о
т
нос
ит
е
л
ь
но
о-алг
е
б
р
9~
1
и
т
2
соо
твет
стве
нн
о
,
п р
и ч е
м
I
~1
I
~
kl' I
~
2
1
~
k
2
п.
н
.,
то
Icov
(1;
1'
;2)
1
~
16k
1
k
2
a
(9~
1'
9(2)'
Д
ля
д
ей ст
в и
те
л
ь
н
ы
х
с.
в
.
~
1
'
~
2
-
к
о
эффициент
16
м
ож
но
за
мени
ть н
а
4.
•
П
у
с
ть
~
1
'
~
2
-
дейс
тви
тел
ь
ны
е
с
.
в
.
И
сп
о
л
ь з
уя
с
во
й
с
т
в
а
услов
ных
м
а
тем
а
т
и
че
с
к
их
о
жида
ни
й,
за
пи
ше
м
Icov (
1;
1'
~2
)I
=
= I
M
~1
[М
(
~
2/9(1)
-
M
~
2]1
~
k
1
M~;
[1\1
(~2
/
9l
1)
-
M
~
2]
= k
1
cov
Х
Х
(~
;,
~
2
)
'
где
~;
= sgn
[М
(~2
/ffi1
)
- М
1;
2]
-
в
е
личин
а,
и
зм
ери
м
ая о
т
нос
ител
ь
но
m
1
•
Повт
орив
э
то
р
а
с
с
уж
д
ени
е
дл
я
~2
'
по
• f
(х)
.::: g
(х),
е
с
л
и
при
дос
та
точ
но
б
ол
ьши
х
х
с
у
щес
т
в
ую
т
к о
н
станты
О
< k
1
< k
2
<
00
т а
ки
е,
что
k
1
f
(
х
)
~ g
(х
)
«; k
2
f
(х
)
.
з·
35

лу
чим
оценку
I
сом
(Sl'
Sz)
l:(; k
1k
1
sup cov
(S;.
s;
).
где
верхняя
грань
беретс
я
по
всем
S;
.
S;
,
и
змерим
ым
от
нос
ительно
9(1
и
9(2
соо
т
в
е
т
с
т
в е
н н
о
и
при
нимающим
значе
ния
1
и
- 1.
П
у
с
т ь
A
={
s; =
1}
,
B={
s; =
1}
.
Тогда
Icov (s;. s;)I
=I
P (AB) +
+
Р
(А
Ё
)
-
Р
(
АВ
)
-
Р
(
А
В)
-
Р
(
А
)
Р
(В
)
-
Р
(А.
)
Р
(8) +
+
Р
(I1)
Р
(8) +
Р
(А
)
Р
(8)
:(;
4а
(9(1'
9(з)
.
Есл
и
величины
SI
и
sz -
ком
плексн
ые,
т
о,
разделяя
действи
те
л
ь
ные
и
мн
и
мы
е
ч
а с
т
и
,
пр
ид
ем
к
требуемом
у
неравенству
(коэффиц
иент
4
за
меня
ет
ся на
16)
.•
Л
емм
а
1.6 .2 [43].
П
у
сть
SI'
Sz
-
действительные
с
.
в.
,
и
змер
имые
относительно
о-алгебр
9(1
и
91
2
со
о
тве
тственно
,
прич
е
м
М
1
GI
I
P
<
00,
м
I SZ,Q<
00
для
не
которых
р
> 1,
а
;»
1.
Т
о
г
д
а
I
COY
(S
I'
bll:(;
1
01
I
s
11Ip IISzllq{a (9(I' 9(z)}I
/S
,
где
s> 1
-1
.
-1
- 1
так
о
е,
что
р
- - q + s = 1.
•
Б
удем
предпола
гать
а
(9l
1
,
9(
2)
>
О,
иначе
нер
авенств
о
триви альн
о.
П
у
с
т
ь
С
= \\ SI
II
p/{a (
9{1
'
9(2
)}I/
P,
С
З
=
11
Szllr/{a
(9(
1' 9(z)}I/Q.
(1
.6.1)
1
Введем
срезки
SI
(
С
1)
=
SI'X.
(1
SI 1:(;
С
1)
,
SZ
(
С
з
)
=
;2'Х.
(1
Szl :(;
С
з
)
'
П
у ст
ь
~
(
С
1
)
= SI -
Gl
(с
1
)
,
[
з
(
С
з
)
=
Sz
- Sz
(с
з
)
·
Т
ог
д
а
I
с
о
у
(SI
'
Sz
)
l:(;
I
с
оу
(SI
(с
1
)
,
sz
(
С
з
) )
!
+ I
СОУ
(SI
(С
1),
~
з
(
cz))
1+
+I
С
ОУ
~
1
(С
1
)
,
sz «,»+ 1
сом
(~
1
(
С
1
)
,
I
z
(cz)
)I
·
(1
.6.2)
П
О
лемме
1.6.1
с
учето
м
(1.6.1)
I
СОУ
(SI
(
С
1
)
,
sZ
(
С
з
) )
!
:(;
4с
1с
з
а
(9(1
'
9(
з)
:(;
:(; 4/1SI
IIp
11
sz
llq
{
а
(9(1
'
9(2)
}I/s.
(1
.6.3)
-т-
I Q Q
П
о
с
к о
л
ь
к у
1\1
1
~з
(C
z)l:(;
С
2-
М
\ Szl .
то
Icov (s]
(с
.
)
,
~
з
(
CZ)
)I
:(;
2с
1М
1
~
(CZ)
I:(;
:(;2
\1
Sl
II
p
\1
sz llQ
{
а
(9(1' 9(z)}I/S.
(1
.6.4)
В
сил
у
симметр
и
и
1cov
~
1
(с
1
)
,
S2
(C
z))
l:(; 2
11
SI
II
p
11
sz
llq
{а
(9(1'
9(z)}I/
S.
(1
.6.5)
Д
а
л
е
е,
[
с
о
м
(fl
(С
1)
,
~2
(с
з))l
:(;
М
1
~
1
(
с)
)
~
з
(Сз)
1
+
м
I
~
1
(с
1
)
1
М
'
~
з
(
с
з
)
!
·
И
сп
оль
зу
я
(1
.6.1)
11
нерав
енство
Г
е
л
ь
д
е
р
а
н
а
х
о
ди
м
М
1~1
(С
)
~2
(
CZ)I
:(;
(
C c
z)I-
Р
Q
/(
РН)
М
(1
SI
11
~2I)P
Q
/(
PH)
~
1
1
36
~
(C
1c
z)
I-PQ
j(pН)
[11
SI II
p
11
G
з
l
lq
)РQ
/(Р
+Q)
~
~ 11SI
II
p
11
sz
ll
Q
{
а
t9?"
9(2)
}I/s.
(1
.6.6)
Аналог
ично
пред
ыдущему
М
1
~
1
(c
1)
1
М
1
~
(C
2
)1
:(;
11
SI
I
l
р
\1
szllQ
{
а
(9( 1'
9C
z
)}'/S. (1.6.7)
П
о
д
с
т
а в
л
я
я
(1
.6.3) - (1.6.7)
в
(1.6.2),
получаем
треб
уемое
. •
Су
щ
ествует
боль
шое
раз н о
обра зие
в
способах
введени
я
меры
з а в
и с и
м
о
с
т и
(Т-алгебр
9(1
и
9l
z
IIЗ
z5
[53, 175, 145].
Е
сли
[(9(1,9(2) -
н
е
о
т
риц
а
т
е
л
ь
н
а я
ф
ункци
я,
равная
Н
УЛЮ
в
сл
у
чае,
ко
гда
а
-алгебры
9( 1
И
9(2
независимы
,
т
о
[t9
c
l'
9(
2)
можно
считать
мерой
за
в
ис
и
мос
т
и
.
Н
а
и
б о
л
е е
часто
и
спол
ь
з
у
ют
с
я
м
еры
з
а
в
и
с
и
м
ос т
и
сле
д
ующего
типа
:
[p ,Q (9ll'
9(2)
= sup{[
Р
(АВ)
-
Р
(
А
)
Р
(B)I/{ [P
(А
)
]Р
[
Р
(в)]
Ч},
А
Е
9(1'
В
Е
9(з,
Р
(А)
>
О
,
Р
(В)
>
О
}
,
р
,
q
Е
[
О,
1]
(1
.6.8)
(м
ера
за
в и
с
и
м
о
с
т
и
[0.0
(9(1'
9(2)
введена
М.
Р
о
з е
н б
л
а
т т
о
м
[1
7
8J
,
[1 ,0
(~
1'
9(
з)
-
И.
А.
Ибра
гим
овым
[52], [ }.I
(9(19(2)
-
Р
.
Сер
флингом
[182]).
Введем
некоторые
условия
п
ер
емешивания
для
слу
ч
айных
R
m
по
л
е
й
S:Q
:(;
R
n
~
,
n
~
1,
т
~
1.
П
у
с
т
ь в
R
n
выделен
а
с
ис
т
е
ма
и
зм
еримых
мн
оже
ств
9Л
и
к
ажд
ому
.1
Е
9л
с
о
п о
с
т
ав
лена
наим
еньшая
а-
а
лг
е
б
р
а
ЭС
(.1)
,
п
орожде
нная
систем
ой
С
.
в.
{s
(Х
)
,
Х
Е
д}.
О
п
р
е
д
е
лим
ко
эффициен
ты
перемеши
ва
ния
а
(
г)
=
= sup
а
(9(
(.11)
' 9(
(.12
))'
Г
де
вер
хня
я
г
р
а
н
ь
берется
п о
всем
п
арам
множе
с
тв
.11'
д
2
Е
9Л,
р ас
ст
оян
ие
между
кот
о
рыми
не
м
еньш
е
г;
а
(г
,
d) = sup
а
(ЭС
(.11)'
9(
(.12))
'
Г
де
с
упремум
ра
с
с
м
а
т
р
и в
а е
т
с
я
по
всем
п
арам
множе
ств
.11' .12
Е
9л
диаметр
а
не
больше
d,
ра
сположенным
на
расстояни
и
не
м
е
н
ьш
е
г
.
Если
не
налагать
о
гр
ан
ичения
на
диаметры,
то
к
о
эффициент
а
(
г
,
00)
превр
ащается
в
а
(г).
Е
сли
9л
-
систе
м
а
парал
лелеп
ипедов,
то
коэффициенты
а
(
г)
и
а
(
г
,
d)
будем
обозна
чать
а*
(
г)
и
а*
(
г
,
d)
соответствен
но
.
В
э
т о
м
с
л
у
ч
а
е
верхняя
грань
берется
по всем
п
а
р
а
л л
е
л
е
ли
пед
ам
П
1
и
П
2
•
которые
:
Г
)
имеют
диаме
тр не
б
ольше
d;
2)
рас
поло
жены
н
а
р
а с с
т
о
ян
и и
не
мень
ше
г.
Коэффициент
а
(г)
введен
Р.
л
.
Доб
руши
ным
(46],
а
ко
эффициенты
а
(
г.
d)
и
а*
(г,
d)
п
р
е
д
л
о
ж
ен
ы
А
.
В
.
Б
у л
и
н
е
к
и
м.
И
.
Г.
Ж
урбе
нко
[22].
С
мысл
п
о сле
д
них
сос
тоит
в
ТОМ
,
ч т
о
з а
в
и
с
и
м
о
с
т
ь
а
-а
лгебр
эс
(.11)
и
9(
(.12)
может
р
а
с
ти
с
ро стом
мн
ожеств
.11
и
.12
'
если
расстояние
между
ними
сохра
няется
,
и
эта
э а
в и
с
и
м
о
с
т ь
будет
ослабевать
,
если
м
ножества
,~
\
и
.12
удаляются
и
их
диаметры
н
е
а р
е
в
ос
х
о
дят
заданной
вели
чи
н
ы
d.
37
