Лекции - Системный анализ сложных систем управления
Подождите немного. Документ загружается.


Т – множество её значений (термов), являющихся наименованиями НП; областью
определения каждой из переменных является множество U;
G – синтаксическая процедура (имеющая форму грамматики), порождающая название,
исходя из терм-множества (конкретное название х, порожденное G, называется термом);
М – семантическая процедура, которая ставит в соответствие каждой нечеткой переменной
её смысл М(х), т.е. нечеткое подмножество М(х) универсального множества U (функция
принадлежности).
Пример 1.
Пример 2. Оценка стоимости выпускаемой продукции. Пусть max стоимость 5 тыс. руб.
ЛП=
[ ]
MGTстоимость ,,5000,0,,
T – {малая, небольшая, средняя, высокая};
G – процедура перебора элементов множества Т;
М – процедура экспертного опроса, позволяющая дать лингвистическую оценку стоимости.
ЛП – могут быть разделены на числовые и нечисловые. Числовые ЛП – переменная, для
которой областью определения Х является подмножество множества действительных чисел
R
1
. Нечеткие переменные, соответствующие значениям числовой лингвистической
переменной называются нечеткими числами. Если множество Х конечно или счётно, то
нечеткие числа называются дискретными.
Пример нечисловой ЛП – переменная качества со значениями «удовлетворительное,
высокое, невысокое».
К основным вопросам, возникающим при разработке и реализации моделей принятия
решений при нечеткой исходной информации, можно отнести следующие:
построение функций принадлежности нечетких множеств;
выполнение операций над нечеткими числами;
сравнение и упорядочение нечетких множеств и чисел;
разработка моделей принятия решений.
51
1
T
µ
2
T
µ
3
T
µ
Х (возраст)
Т
1
(молодой) Т
1
(средний) Т
1
(старый)
uu u
7.3. Построение функций принадлежности. Прямые и косвенные методы
Во всех случаях функция принадлежности строится методами экспертного опроса. В
прямых методах эксперты непосредственно указывают степень принадлежности для каждого
элемента. Методы простые, но имеют высокую степень субъективизма. Для уменьшения
степени субъективизма используют различные приемы, например:
1. усреднение по числу экспертов;
2. параметрическое представление функции принадлежности.
Рассмотрим более подробно второй прием.
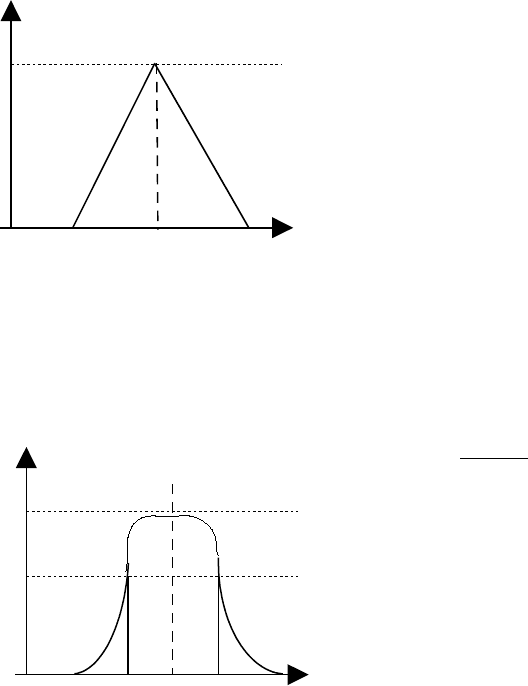
Функции принадлежности треугольного типа:
µ
x
1
x
*
x
11
0)(0)(0)(:0
≠+
′
=−
′
=
′
>∀
δµδµµδ
xxx
0)(0)(0)(:0
=+
′′
≠−
′′
=
′′
>∀
δµδµµδ
xxx
))((max1*)( xx
µµ
=
Левая и правая граница и вершина.
Колоколообразные функции принадлежности (например «Х приближенно равен K»):
µ
1
0,5
0
а k b
2
)(
)(
xk
K
ex
−−
=
α
µ
2
5,0ln4
β
α
=
ab
−=
β
В косвенных методах значения функции принадлежности выбираются таким образом,
чтобы удовлетворить заранее сформированным условиям (вычисляются по определенным
правилам из информации экспертного опроса).
Метод равноделения (метод психологического шкалирования).
Пусть U – универсальное множество, а u
m
и u
M
элементы с min и max степенями
принадлежностями. Для определенности примем
0)(
=
m
u
µ
,
1)(
=
M
u
µ
. Алгоритм метода:
1. найти среднюю по принадлежности точку интервала [u
m
,u
М
]: u
0,5
5,0)(
5,0
=
u
µ
;
2. найти среднюю по принадлежности точку интервала [u
0,5
,u
М
]: u
0,75
;
3. найти среднюю по принадлежности точку интервала [u
m
,u
0,5
]: u
0,25
;
4. найти среднюю по принадлежности точку интервала [u
0,25
,u
0,75
] для проверки
согласованности, если это не u
0,5
, то найденные точки изменяются до получения
согласованности;
5. шаги 1-4 необходимо повторить для получения большого числа точек;
52

6. по набору точек
{ }
µ
µ
,u
определяется искомая функция принадлежности подходящим
методом интерполяции.
Метод попарного сравнения.
Обработка матрицы оценок, отражающих мнение эксперта об относительной
принадлежности элементов множеству или степени выраженности у них свойств,
формализуемого множеством. Потребуем, чтобы для всех элементов множества S
выполнялось равенство
∑
=
=
n
i
S
x
1
1)(
µ
.
Степень принадлежности будем определять посредством парных сравнений. Оценка
элемента x
i
по сравнению с x
j
с точки зрения свойства S -
)(
)(
jS
iS
ij
x
x
a
µ
µ
=
. Для обеспечения
согласованности примем
ji
ij
a
a
1
=
. Итак, мы имеем матрицу оценок
ij
aA
=
. Найдем
),...(
1 n
w
ωω
=
собственный вектор матрицы А, решая уравнение
λ ωω
=⋅
A
, где λ
собственное значение матрицы А. Вычисленные значения
i
ω
принимаются за
iiS
x
ωµ
=
)(
ni ,1
=
. Т.к. всегда выполняется равенство
ωω
nA
=
, то найденные значения тем точнее, чем
ближе
max
λ
к n. Отклонения
max
λ
от n может служить мерой согласованности суждений
экспертов при составлении матрицы оценок.
Нахождение собственного вектора и собственных чисел матрицы.
Иногда приходится рассматривать уравнения типа:
ωλω
⋅=⋅
A
, (7.1)
где
ω
- неизвестный числовой вектор, высота которого равна порядку
A
, а
λ
неизвестное
число. При любом
λ
уравнение (7.1) обладает тривиальным решением
ω
, однако нас будут
интересовать только такие
λ
, при которых эта система имеет нетривиальные решения, эти
значения
λ
называются собственными значениями матрицы А, а решения
ω
при таких
значениях - её собственными векторами. Преобразуем (7.1), используя очевидное равенство:
ωω
⋅=
E
, тогда получаем
( )
0
=−
ωλ
EA
.
(7.2)
Выражение (7.2) представляет собой систему из n однородных алгебраических уравнений с n
неизвестными. Для наличия нетривиального решения необходимо и достаточно, чтобы
0)det(
=−
EA
λ
. Это уравнение называется характеристическим уравнением матрицы
A
, оно
служит для разыскания собственных значений
λ
.
=
333
222
111
cba
cba
cba
A
0
333
222
111
=
−
−
−
λ
λ
λ
cba
cba
cba
Раскрыв определитель, получим алгебраическое уравнение степени n (порядок матрицы А).
Матрица прядка «n» имеет «n» собственных значений. Обычно выбирают максимальное по
модулю значение.
Найдя какое либо собственное значение
λ
, мы можем соответственно собственные
вектора найти из (2). Из этого уравнения вытекает, что при зафиксированной
λ
сумма
решений
21
ωω
+=
y
будет снова решением, произведение
ω
ky
=
решения на число будет
также решением уравнения. Значит, совокупность всех собственных векторов, отвечающих
заданному собственному значению, образует линейное пространство (бесконечное число
ненулевых решений, система обязательно зависима, т.е. одно уравнение является следствием
остальных, одно из уравнений можно отбросить и задавать произвольные значения для
53

одной из переменных). Для нахождения единственного собственного вектора используется
замена одного из уравнений условием нормировки.
Пример. Оценка освещенности предмета в зависимости от расстояния до источника:
предмет в 9, 15, 21 и 28 единицах длины.
Шкала для определения матрицы суждений
Оценка
важности
Качественная оценка Примечание
1 Одинаковая значимость По данному критерию альтернативы
имеют одинаковый ранг
3 Слабое превосходство Соображения о предпочтении одной
альтернативы перед другой
малоубедительны
5 Сильное или существенное
превосходство
Имеются надежные доказательства
существенного превосходства одной
альтернативы
7 Очевидное превосходство Существуют убедительные свидетельства в
пользу одной альтернативы
9 Абсолютное превосходство В высшей степени убедительное
превосходство
2,4,6,8 Промежуточные значения
между соседними оценками
Эксперимент дал матрицу
14/16/17/1
414/16/1
6415/1
7651
=
A
. Сначала находим λ. Для этого составляем
уравнение
0)(
=−
WEA
λ
. Эта неоднородная система имеет нетривиальное решение тогда и
только тогда, когда определитель матрицы
EA
λ
−
равен 0.
0715,2914,64
14/16/17/1
414/16/1
6415/1
7651
34
=−−−=
−
−
−
λλλ
λ
λ
λ
390,4
305,1140,0
305,1140,0
362,0
4
3
2
1
=
−−=
+−=
−=
λ
λ
λ
λ
i
i
Следовательно
390,4
max
=
λ
0
390,414/16/17/1
4390,414/16/1
64390,415/1
765390,41
4
3
2
1
=⋅
−
−
−
−
ω
ω
ω
ω
Система имеет только нулевое решение,
для нахождения собственного вектора
ω
используется замена одного из уравнений
системы условием нормировки
ω
1
+
ω
2
+
ω
3
+
ω
4
=1. Решая новую систему,
получаем:
ω
1
=0,619,
ω
2
=0,235,
ω
3
=0,101,
ω
4
=0,045.
390.04390,4
max
=−=−
n
λ
(степень
согласованности суждений экспертов).
54

7.4. Арифметические операции над нечеткими числами
Под нечетким числом будем понимать нечеткое множество с областью определения в
виде интервала действительной оси R
1
. Пусть А и В – два нечетких числа с носителями S
A
=(a
1,
a
2
) и S
B
=(b
1,
b
2
) соответственно: a
2
>a
1
и b
2
>b
1
.
Согласно принципу обобщения нечеткое число
BAD
⊗=
определяется функцией
принадлежности:
)}(),(min{sup)( bax
BAD
µµµ
=
⊗ = +, -, ⋅, /
x=a
⊗
b
a
∈
S
A
b
∈
S
B
Первоначально принцип обобщения был введен как некоторый эвристический прием,
затем он был получен дедуктивно, а его физический смысл был объяснен в рамках
вероятностной интерпретации функции принадлежности.
Носитель S
D
нечеткого числа D можно найти по правилам интервальной арифметики
S
D
={x:x= a⊗b, a∈S
A
, b∈S
B
}.
Очевидно, что в множестве S
A
×
S
B
для любого x
∈
S
A
⊗S
B
, где операция ⊗ над
носителями нечетких чисел А и В выполняется по правилам интервальной арифметики
существует бесконечно много пар (а,b) таких, что x=a
⊗
b.
Пусть
++=
7
4.0
6
8.0
5
1.0
A
и
++=
6
3.0
5
9.0
4
2.0
B
. Тогда получаем
++++=+
13
3.0
12
4.0
11
8.0
10
2.0
9
1.0
BA
+++++++=⋅
42
3,0
36
3,0
35
4,0
30
8,0
28
2,0
25
1,0
24
2,0
20
1,0
BA
В случае непрерывных нечетких чисел для вычисления результата выполнения
арифметической операции разработано несколько алгоритмов (алгоритм перебора, алгоритм
для кусочно-непрерывной функции принадлежности (требуется числовое решение
нелинейных уравнений или ряда задач безусловной оптимизации)).
Другой способ вычисления может быть использован в случае треугольных функций
принадлежности. Пусть Х - нечеткое число, определим левую
x
′
, правую
x
′′
границы
нечеткого числа и его вершину:
0)(0)(0)(:
≠+
′
=−
′
=
′
∀
δµδµµδ
xxx
0)(0)(0)(:
=+
′′
≠−
′′
=
′′
∀
δµδµµδ
xxx
1*)(
=
x
µ
Можно доказать, что нечеткое число
YXZ
⊗=
также определяется функцией
принадлежности треугольного типа, границы и вершина которой находятся следующим
образом
yxz
′
⊗
′
=
′
,
yxz
′′
⊗
′′
=
′′
,
***
yxz
⊗=
.
Связь четких и нечетких значений лингвистической переменной.
Система управления запасами сформировала решение: закупить небольшое количество
деталей. Нечеткое понятие «небольшое количество» задано дискретным нечетким числом
+
Сколичествонебольшое ,50,1,""
++++++++++++++++=
+
...
35
0
34
2,0
33
4,0
32
8,0
31
9,0
30
0,1
...
22
0,1
21
9,0
...
13
2,0
12
15,0
11
1,0
10
0
...
1
0
С
.Но закупить можно лишь четкое количество деталей, необходимо произвести выбор четкого
значения лингвистической переменной КОЛИЧЕСТВО ДЕТАЛЕЙ при наличии её нечеткого
55
значения «НЕБОЛЬШОЕ». Аналогичных ситуаций в реальных задачах принятия решений
достаточно много. Для решения данной задачи в литературе предложен ряд процедур,
например:
1. каждый раз выбирать
)(suparg* xx
S
Xx
µ
∈
=
.
2. всегда выбирать такой элемент
Xx
∈
0
, который делит площадь под графиком
функции принадлежности пополам
∫ ∫
∞−
+ ∞
∞−
=
0
)(
2
1
)(
X
EE
dxxdxx
µµ
7.5. Сравнение нечетких чисел
Результат расчетов в модели принятия решений в нечёткой среде (интегральная
оценка альтернативы), как правило, является нечётким числом. Поэтому необходимо
определить процедуру сравнения нечётких чисел. Рассмотрим два нечетких числа:
A
RA
µ
,,
1
и
B
RB
µ
,,
1
, у которых
0
≠
BA
SS
.
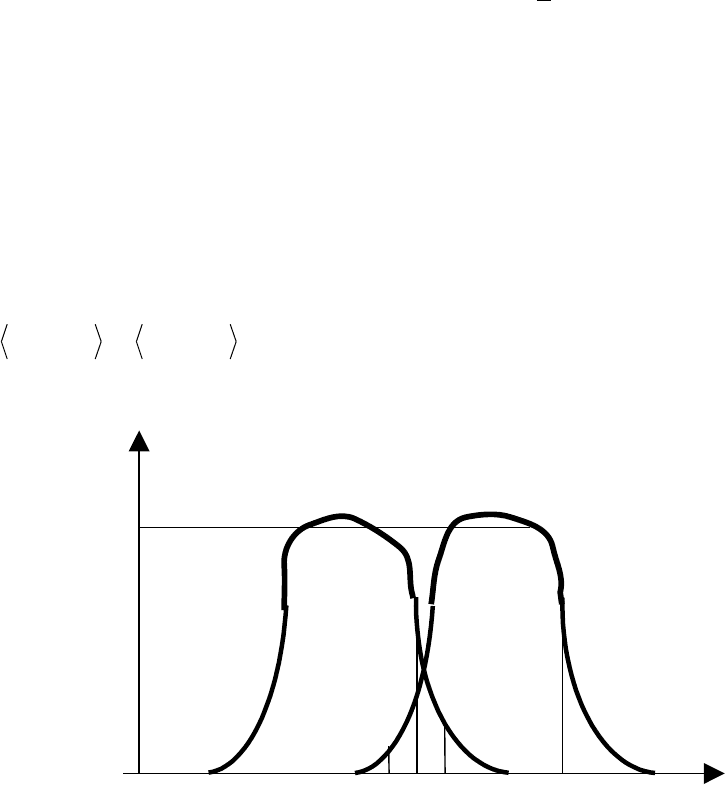
В разных реализациях соотношения между четкими значениями нечетких чисел (а значит, и
между именами нечетких чисел) может быть различным
1: ситуация b
1
>a
1
(A<B);
2: ситуация a
2
>b
2
(A>B).
Таким образом, в общем случае отношения порядка типа «больше, меньше» и т.п. на
множестве нечетких чисел являются нечеткими. Лишь в том случае, когда пересечение
носителей нечетких чисел А и В пусто, отношение между числами будет чётким.
Все предложенные процедуры основаны на вычислении некоторой четкой функции Н
(А,В) от нечетких аргументов А и В, которая называется индексом ранжирования. Значения
индекса для конкретной пары чисел дает основание решить вопрос о том, какое из двух
чисел больше (или с какой степенью больше). Будем использовать в дальнейшем следующий
индекс ранжирования:
{ }
ba
ba
BAH
µµ
,minsup),(
1
5
≥
=
56
µ
)(x
A
µ
)(x
B
µ
2
b
2
a
1
a
1
b
x

Индекс
1
5
H
выделяет в качестве наибольшего нечеткое число А, у которого величина
)(supargsup x
A
Sx
A
µ
∈
является наибольшей (т.е. число, у которого конец «пика» функции
принадлежности расположен правее). При этом форма функции принадлежности не
учитывается.
Возможность того, что
BA
≥
обозначается
)( BAV
≥
:
))(),((minsup)( baBAV
BA
ba
µµ
≥
=≥
Ответ на вопрос «Может ли
A
быть больше
B
?» нечеткий и представляется как
нечеткое подмножество множества {да, нет}:
{ }
нетBAVдаBAVA /(;/)(
≤≥=
.
Для нашего примера:
)( BAV
≥
=0,48 ;
)( ABV
≥
=1.
Больше ли
A
, чем
B
? Ответ:
нетда
1
,
48,0
.
Возможность для нечеткого числа
M
~
быть больше k нечетких чисел
i
M
~
:
k
k
tt
tt
tt
k
MMM
k
tttMMMMV
≥
≥
≥
=≥
2
1
1
))(),...(),(min(sup)
~
,...
~
,
~~
(
~
1
~~
21
µµµ
Замечание. Используя введенную выше процедуру, можно определить так называемое
«множество оптимальности альтернатив» -
{ }
)(,,/)( iNiiiО
оо
µµ
∈=
– интерпретируется как
степень соответствия альтернативы a
i
понятию «наилучшая альтернатива». R
i
(r
i
) – нечеткая
оценка альтернативы a
i
и
mj
jRiR
ijrr
O
rri
ji
ji
,1
,;
))(),((minsup)(
=
≠∀≥
=
µµµ
.
7.6. Многокритериальный выбор в нечеткой ситуации. Решение как
слияние целей
Пусть имеется множество из m альтернатив А = {а
1
, а
2
, …а
m
}, а также задано n
критериев (целей) С
1
, С
2
,… С
n
. Каждый критерий С может быть введен как нечеткое
множество
{ }
iiС
aаС /)(
µ
=
, где
)(
iC
a
µ
– оценка альтернативы а
i
по критерию С (т.е. степень
соответствия альтернативы понятию, определенному критерием С).
При такой постановке задачи решение ищется следующим образом:
1. находится множество решений
n
CCCD
...
21
=
,
)(min)(
,1
jC
ni
jD
aa
i
µµ
=
=
mj ,1
=
;
2. находится лучшее решение
)(max*)(
,1
jD
mj
D
aa
µµ
=
=
.
Если критерии С
i
имеют различную важность, каждому из них приписывается число
0
≥
i
α
(чем важнее критерий, тем больше
i
α
) и правило выбора принимает вид
n
n
a
CCCD
αα
...
21
21
=
0
≥
i
α
ni ,1
=
∑
=
=
n
i
i
n
1
1
1
α
.
Коэффициенты относительной важности критериев могут определяться на основе
процедуры парного сравнения критериев. Вначале формируется матрица суждений
экспертов В, элементы которой находятся из таблицы (см. ниже) и удовлетворяют
следующим условиям b
ii
=1, b
ij
=1/b
ji
. Затем находится
W
- собственный вектор матрицы B,
соответствующий максимальному собственному значению
max
λ
(
WBW
max
λ
=
).
57

Относительная важность критериев С
i
и С
j
Элемент b
ij
Равная важность 1
Немного важнее 3
Важнее 5
Заметно важнее 7
Намного важнее 9
Промежуточные значения 2, 4, 6, 8
7.7. Оценка и упорядочение альтернатив при аддитивности критериев
Второй метод ранжирования альтернатив. Метод использует аддитивную свертку,
обобщенную на случай нечеткой исходной информации.
Пусть необходимо упорядочить m альтернатив а
1
,а
2
,…а
m
, оцениваемых по n
критериям С
1
,С
2
,…,C
n
. Пусть оценка альтернативы a
i
по критерию C
j
задается нечетким
числом R
ij
, относительная важность каждого критерия задается нечетким числом W
j,
nj ,1
=
.
При такой постановке задачи для нахождения решения необходимо произвести следующие
действия:
1. находится взвешенная оценка i-той альтернативы
∑
=
=
n
j
ijji
RWR
1
(если оценки нормированы). (7.3)
Оценки альтернатив по критериям и коэффициенты относительной важности
задаются функциями принадлежности соответственно
)(
ijR
r
ij
µ
и
)(
jW
j
ωµ
, где
1
, Rr
jij
∈
ω
.
Т.к. в данном случае R
ij
и W
j
являются нечеткими числами, R
i
определяется в соответствии с
(7.3) на основе принципа обобщения.
2. находится множество оптимальности альтернатив. После того, как взвешенные
оценки R
i
получены, необходимо сравнить альтернативы на их основе. Для этого вводится
нечеткое множество О, заданное на множестве индексов альтернатив {1,2,…m} и значение
соответствующей функции принадлежности интерпретируется как характеристика степени
того, насколько альтернатива a
i
является лучшей.
Значение
)(i
O
µ
вычисляется как
mj
jRiR
ijrr
O
rri
ji
ji
,1
,;
))(),((minsup)(
=
≠∀≥
=
µµµ
и равно, как
нетрудно видеть, ординате точки пересечения взвешенной оценки i-той альтернативы и
оценки наилучшей альтернативы.
58
ЛИТЕРАТУРА
1. Бусленко Н.П. Моделирование сложных систем. М.: Наука, 1978.
2. Советов Б.Я., Яковлев С.А. Моделирование систем. – М.: Высшая школа, 2001.
3. Львовский Е.Н. Статистические методы построения эмпирических формул. - М.: Высшая
школа, 1988.
4. Вентцель Е.С. Исследование операций. – М.: Советское радио, 1972.
5. Вентцель Е.С. Исследование операций. Задачи, принципы, методология. М.: Высшая
школа, 2001.
6. Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерные приложения.
– М.: Высшая школа, 2000.
7. Таха Х. Введение в исследование операций. – М.: Издательский дом «Вильямс», 2001.
8. Краснощеков П.С., Петров А.А. Принципы построения моделей. М.: ФАЗИС, ВЦ РАН,
2000.
9. Павловский Ю.Н. Имитационные модели и системы. М.: ФАЗИС, ВЦ РАН, 2000.
10. Борисов А.Н., Алексеев А.В. и др. Обработка нечеткой информации в системах принятия
решений. – М.: Радио и связь, 1989.
11.Борисов А.Н., Крумберг О.А., Федоров И.П. Принятие решений на основе нечетких
моделей. Примеры использования. Рига: Зинатне, 1990.
59
