Лекции - Системный анализ сложных систем управления
Подождите немного. Документ загружается.

приближенно считать показательным, полагая в этой формуле величину
λ
равной среднему
значению
)(t
λ
на том участке, который нас интересует.
2.5. Пуассоновские потоки событий и непрерывные марковские цепи
Рассмотрим некоторую физическую систему S={S
1
,S
2
,…S
n
}, которая переходит из
состояния в состояние под влиянием каких-то случайных событий (вызовы, отказы,
выстрелы). Будем себе это представлять так, будто события, переводящие систему из
состояния в состояние, представляют собой какие-то потоки событий.
Пусть система S в момент времени t находится в состоянии S
i
и может перейти из него
в состояние S
j
под влиянием какого-то пуассоновского потока событий с интенсивностью
λ
ij
:
как только появляется первое событие этого потока, система мгновенно переходит из S
i
в S
j
.
Как мы знаем, вероятность этого перехода за элементарный промежуток времени
t
∆
(элемент вероятности перехода) равна
t
ij
∆
λ
, отсюда вытекает, что плотность вероятности
перехода λ
ij
в непрерывной цепи Маркова представляет собой не что иное, как
интенсивность потока событий, переводящих систему по соответствующей стрелке. Если все
потоки событий, переводящие систему S из состояния в состояние пуассоновские, то
процесс, протекающий в системе, будет марковским.
Проставим интенсивности пуассоновских потоков (плотности вероятностей
переходов) на графе состояний системы у соответствующих стрелок. Получим размеченный
граф состояний. На его основе можно написать уравнения Колмогорова и вычислить
вероятности состояний.
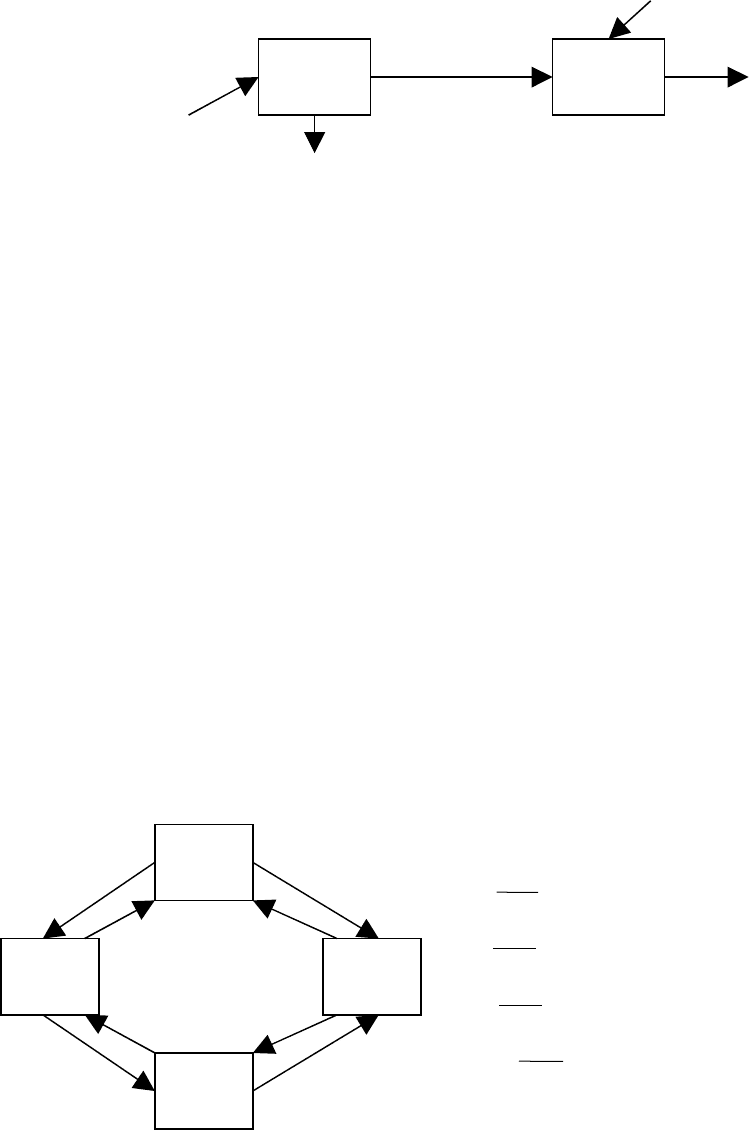
Пример. Техническая система S состоит из двух узлов I и II, каждый из которых
независимо от другого может отказывать. Поток отказов первого узла пуассоновский с
интенсивностью λ
I
, второго также пуассоновский с интенсивностью λ
II
. Каждый узел сразу
после отказа начинает ремонтироваться (восстанавливаться). Поток восстановлений
(окончаний ремонта узла) для обоих узлов – пуассоновский с интенсивностью λ. Составить
граф состояний системы и написать уравнение Колмогорова. Состояния системы: S
11
- оба
узла исправны; S
21
– первый узел ремонтируется, второй исправен; S
12,
S
22
.
t=0 p
11
=1 p
21
=p
22
=p
12
=0
p
11
+p
12
+p
21
+p
22
=1.
11
S
i
S
j
ij
λ
S
11
S
22
S
21
S
12
1
λ
2
λ
2
λ
1
λ
λ λ
λ
2
λ
++−=
+++−=
+++−=
+++−=
122122
22
221112
12
221121
21
122111
11
2
)(
)(
)(
ppp
dt
dp
ppp
dt
dp
ppp
dt
dp
ppp
dt
dp
III
III
III
III
λλλ
λλλλ
λλλλ
λλλλ

2.6. Предельные вероятности состояний
Пусть имеется физическая система S={S
1
,S
2
,…S
n
}, в которой протекает марковский
случайный процесс с непрерывным временем (непрерывная цепь Маркова). Предположим,
что
λ
ij
=const, т.е. все потоки событий простейшие (стационарные пуассоновские). Записав
систему дифференциальных уравнений Колмогорова для вероятностей состояний и
проинтегрировав эти уравнения при заданных начальных условиях, мы получим p
1
(t), p
2
(t),…
p
n
(t),
∑
=
=
n
i
i
tp
1
1)(
при любом t. Поставим следующий вопрос, что будет происходить с
системой S при t
→∞
. Будут ли функции p
i
(t) стремиться к каким-то пределам? Эти пределы,
если они существуют, называются предельными вероятностями состояний. Можно доказать
теорему: если число состояний S конечно и из каждого состояния можно перейти (за то или
иное число шагов) в каждое другое, то предельные вероятности состояний существуют и не
зависят от начального состояния системы. Предположим, что поставленное условие
выполнено и предельные вероятности существуют
ii
t
ptp
=
∞→
)(lim
(i=1,2,…n),
∑
=
=
n
i
i
p
1
1
.
Таким образом, при t
→∞
в системе S устанавливается некоторый предельный
стационарный режим. Смысл этой вероятности: она представляет собой не что иное, как
среднее относительное время пребывания системы в данном состоянии. Для вычисления p
i
в
системе уравнений Колмогорова, описывающих вероятности состояний, нужно положить все
левые части (производные) равными 0. Систему получающихся линейных алгебраических
уравнений надо решать совместно с уравнением
∑
=
=
n
i
i
p
1
1
.
Схема гибели и размножения. Мы знаем, что имея в распоряжении размеченный граф
состояний, можно легко написать уравнения Колмогорова для вероятностей состояний, а
также написать и решить алгебраические уравнения для финальных вероятностей. Для
некоторых случаев удается последние уравнения решить заранее, в буквенном виде. В
частности, это удается сделать, если граф состояний системы представляет собой так
называемую «схему гибели и размножения».
Рис. 2.1 – Схема гибели и размножения.
Граф состояний для схемы гибели и размножения имеет вид, показанный на рис. 19.1.
Особенность этого графа в том, что все состояния системы можно вытянуть в одну цепочку,
в которой каждое из средних состояний (S
1
, S
2
, ..., S
n-1
) связано прямой и обратной стрелкой с
каждым из соседних состояний — правым и левым, а крайние состояния (S
0
, S
n
) — только с
одним соседним состоянием. Термин «схема гибели и размножения» ведет начало от
биологических задач, где подобной схемой описывается изменение численности популяции.
Схема гибели и размножения очень часто встречается в разных задачах практики, в
частности — в теории массового обслуживания, поэтому полезно, один раз и навсегда, найти
для нее финальные вероятности состояний.
Предположим, что все потоки событий, переводящие систему по стрелкам графа,—
простейшие (для краткости будем называть и систему S и протекающий в ней процесс —
простейшими).
Пользуясь графом рис. 2.1, составим и решим алгебраические уравнения для
финальных вероятностей состояний (их существование вытекает из того, что из каждого
12
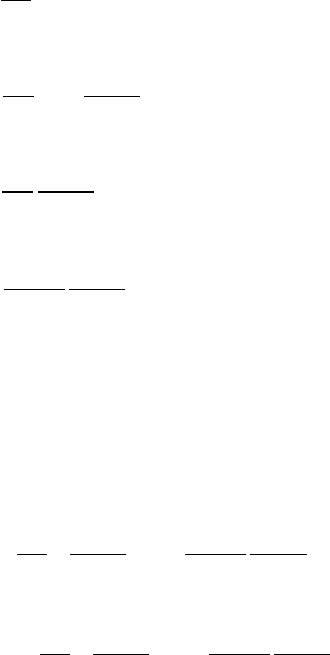
состояния можно перейти в каждое другое, и число состояний конечно). Для первого
состояния S
0
имеем:
0 01 10 1
p p
λ λ
=
(2.1)
Для второго состояния S
1
:
12 10 1 0 01 21 2
( ) p p p
λ λ λ λ
+ = +
В силу (2.1) последнее равенство приводится к виду
1 12 21 2
p p
λ λ
=
далее, совершенно аналогично
2 23 32 3
p p
λ λ
=
и вообще
1 1, , 1k k k k k k
p p
λ λ
− − −
=
где k принимает все значения от 0 до n. Итак, финальные вероятности р
0
, p
1
,..., р
n
удовлетворяют уравнениям
0 01 10 1
1 12 21 2
1 1, , 1
1 1, , 1
......................
..............................
k k k k k k
n n n n n n
p p
p p
p p
p p
λ λ
λ λ
λ λ
λ λ
− − −
− − −
=
ь
п
=
п
п
п
э
=
п
п
п
=
п
ю
(2.2)
кроме того, надо учесть нормировочное условие
p
0
+ р
1
+ р
2
+…+ р
n
=1 (2.3)
Решим эту систему уравнений. Из первого уравнения (2.2) выразим р
1
через р
0
.
01
1 0
10
p p
λ
λ
=
(2.4)
Из второго, с учетом (2.4), получим:
12 01
12
2 1 0
21 21 10
p p p
λ λ
λ
λ λ λ
= =
(2.5)
из третьего, с учетом (2.5),
23 12 01
3 0
32 21 10
p p
λ λ λ
λ λ λ
=
(2.6)
и вообще, для любого k (от 1 до N):
1, ...
12 01
0
, 1... 21 10
k k
k
k k
p p
λ
λ λ
λ λ λ
−
−
=
(2.7)
Обратим внимание на формулу (2.7). В числителе стоит произведение всех
интенсивностей, стоящих у стрелок, ведущих слева направо (с начала и до данного
состояния S
k
), а в знаменателе — произведение всех интенсивностей, стоящих у стрелок,
ведущих справа налево (с начала и до S
k
).
Таким образом, все вероятности состояний p
1
, р
2
, …, p
n
выражены через одну из них
(p
0
). Подставим эти выражения в нормировочное условие (2.3). Получим, вынося за скобку
p
0
:
1, ...
01 12 01 12 01
0
10 21 10 , 1... 21 10
(1 ... ) 1
n n
n n
p
λ
λ λ λ λ λ
λ λ λ λ λ λ
−
−
+ + + + =
отсюда получим выражение для р
0
.
1, ...
1
01 12 01 12 01
0
10 21 10 , 1... 21 10
(1 ... )
n n
n n
p
λ
λ λ λ λ λ
λ λ λ λ λ λ
−
−
−
= + + + +
(2.8)
13
(скобку мы возвели в степень -1, чтобы не писать двухэтажных дробей). Все остальные
вероятности выражены через р
0
(см. формулы (2.4) — (2.7)). Заметим, что коэффициенты при
p
0
в каждой из них представляют собой не что иное, как последовательные члены ряда,
стоящего после единицы в формуле (2.8). Значит, вычисляя р
0
, мы уже нашли все эти
коэффициенты.
Полученные формулы очень полезны при решении простейших задач теории массового
обслуживания.
3. ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ
3.1. Задачи теории массового обслуживания
При исследовании операций часто приходится сталкиваться с работой своеобразных
систем, называемых системами массового обслуживания (СМО). Примерами таких систем
могут служить: телефонные станции, ремонтные мастерские, билетные кассы, справочные
бюро, магазины, парикмахерские и т. п. Каждая СМО состоит из какого-то числа
обслуживающих единиц (или «приборов»), которые мы будем называть каналами
обслуживания. Каналами могут быть: линии связи, рабочие точки, кассиры, продавцы,
лифты, автомашины и др. СМО могут быть одноканальными и многоканальными.
Всякая СМО предназначена для обслуживания какого-то потока заявок (или
«требований»), поступающих в какие-то случайные моменты времени. Обслуживание заявки
продолжается какое-то, вообще говоря, случайное время Т
об
, после чего канал освобождается
и готов к приему следующей заявки. Случайный характер потока заявок и времен
обслуживания приводит к тому, что в какие-то периоды времени на входе СМО скапливается
излишне большое число заявок (они либо становятся в очередь, либо покидают СМО
необслуженными); в другие же периоды СМО будет работать с недогрузкой или вообще
простаивать.
В СМО происходит какой-то СП с дискретными состояниями и непрерывным
временем; состояние СМО меняется скачком в моменты появления каких-то событий (или
прихода новой заявки, или окончания обслуживания, или момента, когда заявка, которой
надоело ждать, покидает очередь). Чтобы дать рекомендации по рациональной организации
этого процесса и предъявить разумные требования к СМО, необходимо изучить СП, описать
его математически. Этим и занимается теория МО.
Предмет теории массового обслуживания — построение математических моделей,
связывающих заданные условия работы СМО (число каналов, их производительность,
правила работы, характер потока заявок) с интересующими нас характеристиками —
показателями эффективности СМО, описывающими, с той или другой точки зрения, ее
способность справляться с потоком заявок. В качестве таких показателей (в зависимости от
обстановки и целей исследования) могут применяться разные величины, например: среднее
число заявок, обслуживаемых СМО в единицу времени; среднее число занятых каналов;
среднее число заявок в очереди и среднее время ожидания обслуживания; вероятность того,
что число заявок в очереди превысит какое-то значение, и т. д. Область применения
математических методов теории МО непрерывно расширяется и все больше выходит за
пределы задач, связанных с «обслуживающими организациями» в буквальном смысле слова.
Как своеобразные СМО могут рассматриваться: ЭВМ, системы сбора и обработки
информации, автоматизированные производственные цеха, поточные линии, транспортные
системы, системы ПВО и т.п.
Математический анализ работы СМО очень облегчается, если процесс этой работы —
марковский. Для этого достаточно, чтобы все потоки событий, переводящие систему из
состояния в состояние (потоки заявок, потоки «обслуживаний»), были простейшими. Если
это свойство нарушается, то математическое описание процесса становится гораздо сложнее
и довести его до явных, аналитических формул удается лишь в редких случаях. Однако все
же аппарат простейшей, марковской теории массового обслуживания может пригодиться
14
для приближенного описания работы СМО даже в тех случаях, когда потоки событий — не
простейшие. Во многих случаях для принятия разумного решения по организации работы
СМО вовсе и не требуется точного знания всех ее характеристик — зачастую достаточно и
приближенного, ориентировочного. Причем, чем сложнее СМО, чем больше в ней каналов
обслуживания, тем точнее оказываются эти приближенные формулы.
3.2. Классификация СМО и их основные характеристики
Системы массового обслуживания делятся на типы (или классы) по ряду признаков.
Первое деление: СМО с отказами и СМО с очередью. В СМО с отказами заявка,
поступившая в момент, когда все каналы заняты, получает отказ, покидает СМО и в
дальнейшем процессе обслуживания не участвует. Примеры СМО с отказами встречаются в
телефонии: заявка на разговор, пришедшая в момент, когда все каналы связи заняты,
получает отказ и покидает СМО необслуженной. В СМО с очередью заявка, пришедшая в
момент, когда все каналы заняты, не уходит, а становится в очередь и ожидает возможности
быть обслуженной. На практике чаще встречаются (и имеют большее значение) СМО с
очередью; недаром теория массового обслуживания имеет второе название: «теория
очередей».
СМО с очередью подразделяются на разные виды, в зависимости от того, как
организована очередь—ограничена она или не ограничена. Ограничения могут касаться как
длины очереди, так и времени ожидания (так называемые «СМО с нетерпеливыми
заявками»). При анализе СМО должна учитываться также и «дисциплина обслуживания» —
заявки могут обслуживаться либо в порядке поступления (раньше пришла, раньше
обслуживается), либо в случайном порядке. Нередко встречается так называемое
обслуживание с приоритетом — некоторые заявки обслуживаются вне очереди. Приоритет
может быть как абсолютным — когда заявка с более высоким приоритетом «вытесняет» из-
под обслуживания заявку с низшим (например, пришедший в парикмахерскую клиент
высокого ранга прогоняет с кресла обыкновенного клиента), так и относительным — когда
начатое обслуживание доводится до конца, а заявка с более высоким приоритетом имеет
лишь право на лучшее место в очереди.
Существуют СМО с так называемым многофазовым обслуживанием, состоящим из
нескольких последовательных этапов или «фаз» (например, покупатель, пришедший в
магазин, должен сначала выбрать товар, затем оплатить его в кассе, затем получить на
контроле).
Кроме этих признаков, СМО делятся на два класса: «открытые» и «замкнутые». В
открытой СМО характеристики потока заявок не зависят от того, в каком состоянии сама
СМО (сколько каналов занято). В замкнутой СМО — зависят. Например, если один рабочий
обслуживает группу станков, время от времени требующих наладки, то интенсивность
потока «требований» со стороны станков зависит от того, сколько их уже неисправно и ждет
наладки. Это — пример замкнутой СMO.
В зависимости от типа СМО при оценке её эффективности могут применяться те или
иные величины (показатели эффективности). Например, для СМО с отказами одной из
важнейших характеристик её продуктивности является так называемая абсолютная
пропускная способность – среднее число заявок, которое может обслужить система за
единицу времени. Наряду с абсолютной, часто рассматривается относительная пропускная
способность – средняя доля поступивших заявок, обслуживаемая системой (отношение
среднего числа обслуживаемых в единицу времени заявок к среднему числу поступающих
заявок за это время). Помимо этого при анализе СМО с отказами могут интересовать ещё
среднее число занятых каналов, среднее относительное время простоя системы в целом и
отдельного канала и т.д.
Характеристики СМО с ожиданиями. Для СМО с неограниченным ожиданием
абсолютные и относительные пропускные способности теряют смысл. Зато важными
15
являются: среднее число заявок в очереди, среднее число заявок в системе (в очереди и под
обслуживанием), среднее время ожидания заявки в очереди, среднее время пребывания
заявки в системе и другие. Для СМО с ограниченным ожиданием интерес представляют обе
группы характеристик.
Для анализа процесса, протекающего в СМО, существенно знать основные параметры
системы: число каналов n, интенсивность потока заявок λ, производительность каждого
канала (среднее число заявок
µ
, обслуживаемых непрерывно занятым каналом в единицу
времени), условия образования очереди (ограничения, если они есть).
Условимся все потоки событий, переводящие СМО из состояния в состояние, считать
пуассоновскими.
3.3. Одноканальная СМО с отказами
Простейшая задача. Пусть СМО состоит только из одного канала (n=1) и на нее
поступает пуассоновский поток заявок с интенсивностью λ, зависящей в общем случае от
времени
λ
=
λ
(t). (3.1)
Заявка, заставшая канал занятым, получает отказ и покидает систему. Обслуживание
заявки продолжается в течение случайного времени Т
об
, распределенного по показательному
закону с параметром µ
f(t)=
µ
e
-
µ
t
(t
>
0). (3.2)
Из этого следует, что «поток обслуживаний» - простейший, с интенсивностью µ.
Требуется найти: абсолютную (А) и относительную (q) пропускные способности.
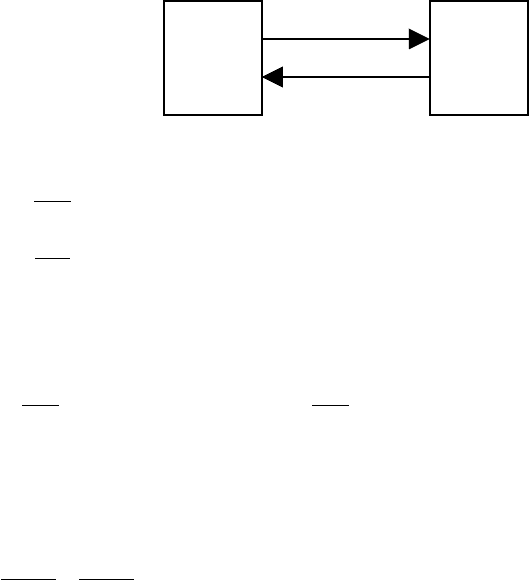
Рассмотрим единственный канал обслуживания как физическую систему S, которая
может находиться в одном из двух состояний: S
0
– свободен, S
1
– занят. Обозначим
вероятности состояний p
0
(t) и p
1
(t). Очевидно:
∀
t p
0
(t)+p
1
(t)=1 (3.3).
Граф состояний системы :
По графу состояний системы составим дифференциальные уравнения Колмогорова:
+−=
+−=
01
1
10
0
pp
dt
dp
pp
dt
dp
λµ
µλ
(3.4)
В соответствии с (3.3) одно уравнение в (3.4) лишнее. Отбросим второе уравнение, а
первое перепишем с учетом (3.3):
)1(
00
0
pp
dt
dp
−+−=
µλ
или
µλµ
++−=
0
0
)( p
dt
dp
(3.5).
Это уравнение естественно решать при начальных условиях p
0
(0)=1; p
1
(0)=0.
Уравнение (3.5) легко может быть решено не только для простейшего потока заявок
(λ=const), но и для случая λ=λ(t). Приведем решение (3.5) только для случая λ=const:
t
ep
)(
0
µλ
µλ
λ
µλ
µ
+−
+
+
+
=
.
16
S
0
S
1
λ
µ
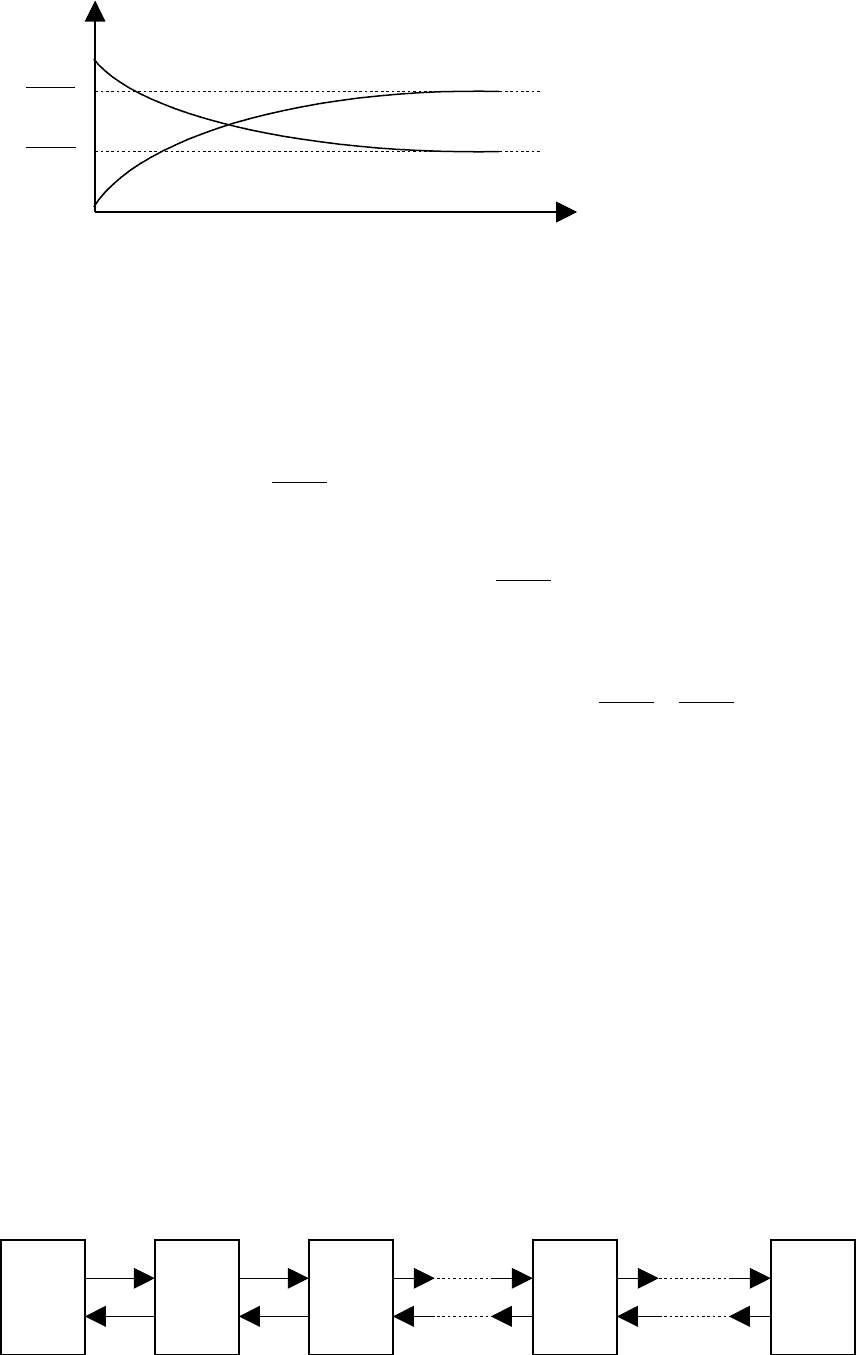
Для нашего случая вероятность p
0
есть не что иное, как q.
Действительно, p
0
есть вероятность того, что в момент t канал свободен, иначе
вероятность того, что заявка, пришедшая в момент t, будет обслужена. А значит, для данного
момента времени t среднее число обслуженных заявок к числу поступивших также равно p
0
:
q= p
0
.
В пределе, при t
→∞
, когда процесс обслуживания уже установится, предельное
значение q будет равно
µλ
µ
+
=
q
.
Легко найти и А, зная q. Они связаны очевидным соотношением:
qA
λ
=
. В пределе,
при t
→∞
, А тоже установится и будет равна
µλ
λ µ
+
=
A
.
Зная q (вероятность того, что пришедшая в момент t заявка будет обслужена) легко
найти вероятность отказа: P
отк
=1-q. P
отк
есть не что иное, как средняя доля необслуженных
заявок среди поданных. В пределе, при t
→∞
µλ
λ
µλ
µ
+
=
+
−=
1
отк
P
.
3.4. Многоканальная СМО с отказами
Рассмотрим n-канальную СМО с отказами. Будем нумеровать состояния системы по
числу занятых каналов (или, что в данном случае то же, по числу заявок, связанных с
системой). Состояния будут:
S
0
– все каналы свободны;
S
1
– занят ровно один канал, остальные свободны;
……
S
k
– заняты ровно k каналов, остальные свободны;
…….
S
n
– заняты все n каналов.
Граф состояний имеет следующий вид. Слева направо систему переводит один и тот
же поток – поток заявок с интенсивностью λ.
Очевидно, если обслуживанием занято 2 канала, а не один, поток обслуживаний,
переводящий систему по стрелке S
2
→
S
1
, будет вдвое интенсивнее (2
µ
), если занято k-
17
)(
0
tp
)(
1
tp
P
t
µλ
λ
+
µλ
µ
+
0
S
0
S
1
S
2
S
k
S
n
λ
λ
λ
λ
λ
λ
µ
2µ
3µ
k
µ
(k+1)
µ
n
µ
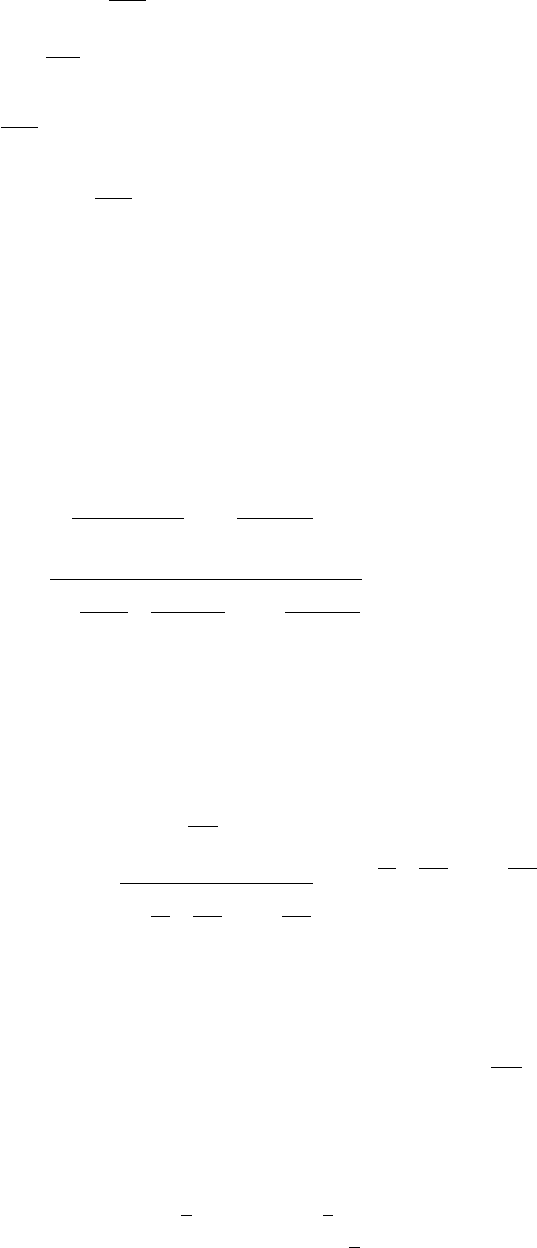
каналов – в k раз интенсивнее (k
µ
). Процесс такого вида представляет собой частный случай
процесса гибели и размножения. Составляем уравнения Колмогорова:
+−=
++++−=
+++−=
+−=
−
+−
1
11
.......
201
......
1
10
0
)1()(
2)(
nn
n
kkk
k
ppn
dt
dp
pkppk
dt
dp
ppp
dt
dp
pp
dt
dp
λµ
µλµλ
µλµλ
µλ
(3.6)
Уравнения (3.6) называются уравнениями Эрланга. Естественными начальными условиями
являются:
p
0
(0)=1; p
1
(0)=p
2
(0)=…=p
n
(0)=0
Интегрировать (6) в аналитическом виде довольно сложно, на практике решают численно с
использованием ЭВМ. Такое решение дает нам все вероятности состояний как функции
времени: p
0
(t), p
1
(t), …, p
n
(t).
Больше всего интересны предельные вероятности состояний, характеризующие
установившийся режим работы СМО (при t
→∞
). Воспользуемся готовым решением,
полученным для схемы гибели и размножения:
++++
=
=
⋅⋅
=
!
)/(
...
!2
)/(
!1
/
1
1
!
)/(
...2
2
0
00
n
p
p
k
p
k
p
n
kk
k
µλµλµλ
µλ
µµµ
λ
(k=1,2,..n) (3.7)
Обозначим
ρµλ
=
/
и будем называть величину
ρ
«приведенной интенсивностью» потока
заявок. Физический смысл её таков: величина
ρ
представляет собой среднее число заявок,
приходящих в СМО за среднее время обслуживания одной заявки. С учетом этого (3.7)
принимает вид (формулы Эрланга):
1
2
2
0
0
!
...
!2!1
1
!
...
!2!1
1
1
!
−
++++=
++++
=
=
n
n
p
p
k
p
n
n
k
k
ρρρ
ρρρ
ρ
(3.8)
Теперь можно найти характеристики эффективности СМО: q, А, Р
отк
.
Заявка получает отказ, если приходит в момент, когда все n каналов заняты. Вероятность
этого равна:
0
!
p
n
pP
n
nотк
ρ
==
.
Вероятность того, что заявка будет принята к обслуживанию (она же q) дополняет
Р
отк
до 1: q = 1-p
n
. И наконец: А=
λ
q=
λ
(1- p
n
).
Одной из важных характеристик СМО с отказами является среднее число занятых каналов (в
данном случае оно совпадает со средним числом заявок, находящихся в системе). Обозначим
это среднее число
k
. Величину
k
можно вычислить непосредственно по формуле:
n
npppk
++⋅+⋅=
...10
10
как математическое ожидание дискретной случайной величины, принимающей значение 0,1,
…n с вероятностями p
0
, p
1
…p
n
.
18
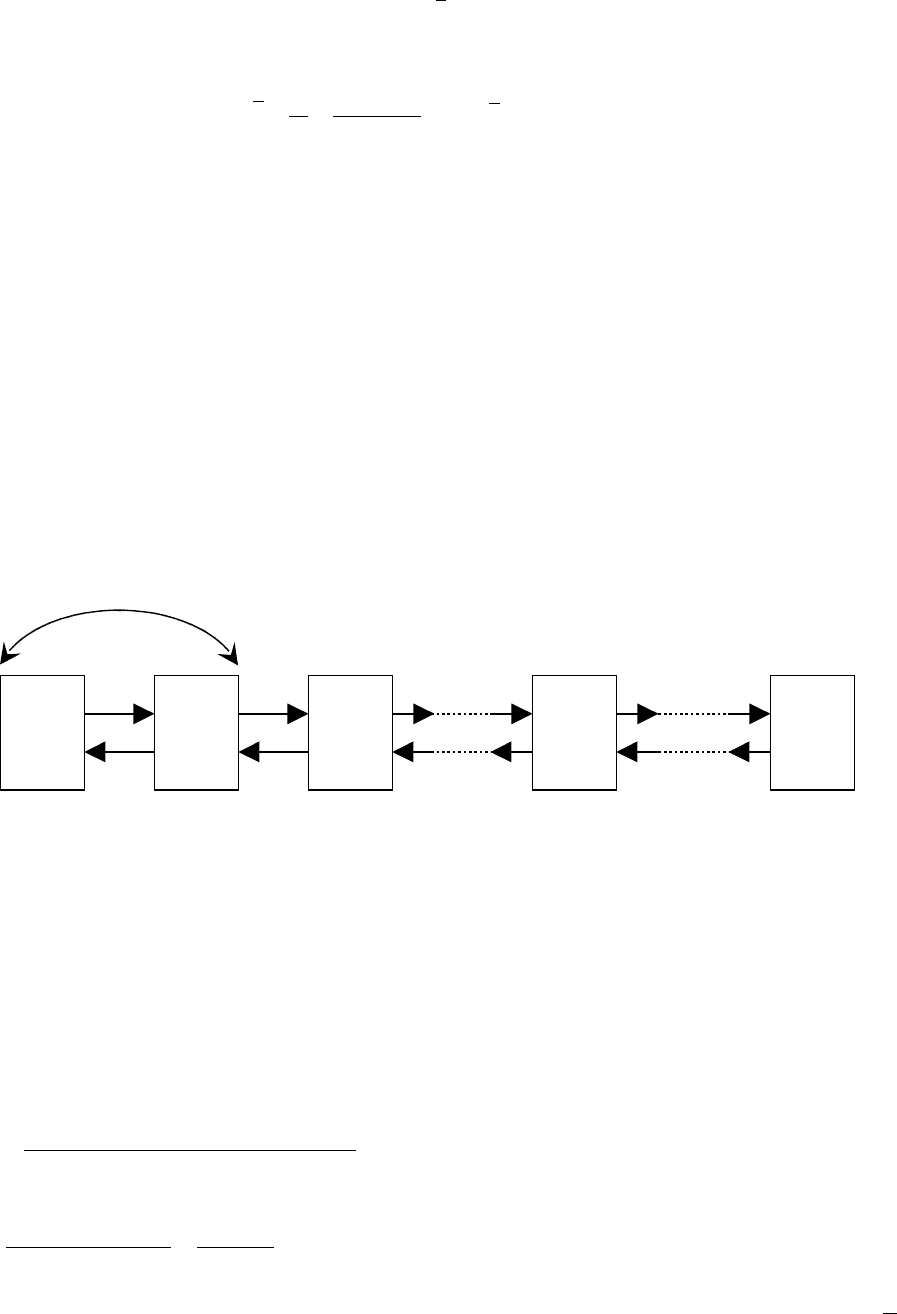
Однако значительно проще выразить
k
через А . А есть не что иное, как среднее
число заявок, обслуживаемых в единицу времени; один занятый канал обслуживает в
среднем за единицу времени µ заявок; следовательно, среднее число занятых каналов
µ
λ
µ
)1(
n
pA
k
−
==
или
)1(
n
pk
−=
ρ
.
3.5. Одноканальная СМО с ожиданием
На СМО поступает поток заявок с интенсивностью λ, интенсивность обслуживания µ
(т.е. в среднем непрерывно занятый канал будет выдавать µ обслуженных заявок в единицу
времени), n=1. Заявка, поступившая в момент, когда канал занят, становится в очередь и
ожидает обслуживания. Предположим, что количество мест в очереди ограничено числом m
(в дальнейшем, при m
→∞
можно получить характеристики одноканальной СМО без
ограничений по длине очереди). Будем нумеровать состояния СМО по числу заявок,
находящихся в системе (как обслуживаемых, так и ожидающих обслуживания):
S
0
– канал свободен; S
1
– канал занят, очереди нет; S
2
– канал занят, одна заявка стоит в
очереди; S
k
– канал занят, k -1 стоят в очереди; S
m+1
– канал занят, m заявок стоят в очереди.
Граф состояний (размеченный) имеет вид:
Снова схема гибели и размножения. Пользуясь общим решением, напишем
выражения предельных вероятностей состояния:
++++
=
=
=
=
=
+
+
+
12
0
0
1
1
0
0
2
2
01
)/(...)/()/(1
1
)/(
....
)/(
....
)/(
)/(
m
m
m
k
k
p
pp
pp
pp
pp
µλµλµλ
µλ
µλ
µλ
µλ
или
[ ]
1
12
0
0
1
1
0
0
2
2
01
...1
....
....
−
+
+
+
++++=
=
=
=
=
m
m
m
k
k
p
pp
pp
pp
pp
ρρρ
ρ
ρ
ρ
ρ
(3.9)
В знаменателе выражения для р
0
стоит геометрическая прогрессия. Суммируя её находим
22
0
1
1
)1/()1(
1
++
−
−
=
−−
=
mm
p
ρ
ρ
ρρ
(3.10)
Уравнение (3.10) справедливо только при
1
≠
ρ
(иначе возникает неопределенность вида
0
0
).
Но сумму геометрической прогрессии со знаменателем
1
=
ρ
найти ещё проще, чем по
(3.10); она равна (m+2) и в этом случае p
0
=1/(m+2) {то же самое получится, если раскрыть
неопределенность по правилу Лопиталя}.
19
S
0
S
1
S
2
S
k
S
m+1
λ
λ
λ
λ
λ
λ
µ
µ
µ
µ
µ
µ
Очерединет
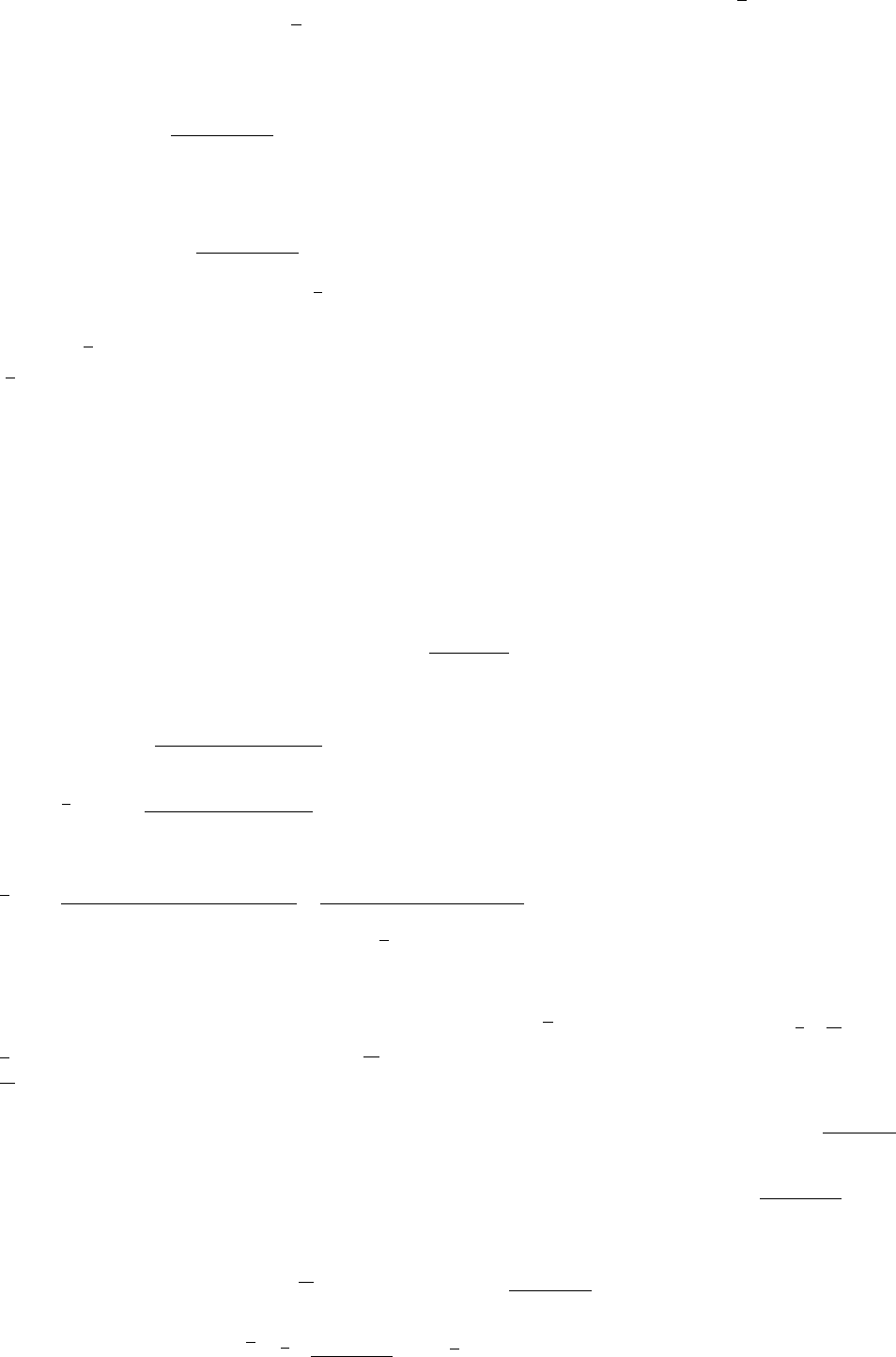
Определим характеристики СМО: Р
отк
q, А, среднюю длину очереди
r
, среднее число
заявок, связанных с системой
k
.
Очевидно, заявка получает отказ только в том случае, когда канал занят и все m мест в
очереди – тоже:
2
1
1
1
)1(
+
+
+
−
−
==
m
m
mотк
pP
ρ
ρρ
(3.11)
2
1
1
)1(
11
+
+
−
−
−=−=
m
m
отк
Pq
ρ
ρρ
(3.12)
А=
λ
q. Найдем среднее число
r
, находящихся в очереди; определим эту величину как
математическое ожидание дискретной случайной величины R – числа заявок , находящихся в
очереди:
[ ]
RMr
=
.
[ ]
12
0
2
0
1
00
3
0
2
132
...)1(...21
...)1(...21
...)1(...21
−−
+
+
++−+++=
=⋅++−++⋅+⋅=
=⋅++−++⋅+⋅=
mk
mk
mk
mkp
pmpkpp
pmpkppr
ρρρρ
ρρρρ
.
Выведем формулу для суммы. Эта сумма не что иное, как производная по
ρ
суммы
∑
+++++=
−
mk
ρρρρ
......
12
, а для этого выражения мы можем воспользоваться формулой
суммы геометрической прогрессии:
∑
−
−
=
+
ρ
ρρ
1
1m
Продифференцируем её по
ρ
и проведя преобразования, найдем
∑
−
−+−
=
'
2
)1(
)1(1
ρ
ρ
ρρ
mm
m
(3.13).
Тогда
2
0
2
)1(
)1(1
ρ
ρρ
ρ
−
−+−
=
mm
pr
m
.
Подставляем p
0
из (10) и получаем
[ ] [ ]
)1)(1(
)1(1
)1)(1(
)1(1)1(
2
2
22
2
ρρ
ρρρ
ρρ
ρρρ
ρ
−−
−+−
=
−−
−+−−
=
++
m
m
m
m
mmmm
r
(3.14)
Выведем теперь формулу для
k
. Рассмотрим общее число заявок К, связанных с
системой, как сумму двух случайных величин: числа заявок, стоящих в очереди и числа
заявок, находящихся под обслуживанием:
Ω+=
RK
.
По теореме сложения математических ожиданий
[ ] [ ] [ ]
ω
+=Ω+==
rMRMKMk
, где
r
- среднее число заявок в очереди;
ω
- среднее число заявок под обслуживанием. Найдем
ω
. Т.к. канал у нас один, то случайная величина
Ω
может принимать только два значения: 0
или 1. Значение 0 она принимает, если канал свободен; вероятность этого равна
2
0
1
1
+
−
−
=
m
p
ρ
ρ
. Значение 1 она принимает, если канал занят; вероятность этого равна
2
2
0
1
1
+
+
−
−
=−
m
m
p
ρ
ρρ
.
Отсюда находим:
2
2
00
1
)1(10
+
+
−
−
=−⋅+⋅=
m
m
pp
ρ
ρρ
ω
.
2
2
1
+
+
−
−
+=
m
m
rk
ρ
ρρ
, где
r
находим из (3.14).
20
