Лекции - Системный анализ сложных систем управления
Подождите немного. Документ загружается.

Множественность задач выбора:
1.множество альтернатив может быть конечным, счетным или континуальным;
2.оценка альтернативы по одному или нескольким критериям, которые имеют как
качественный, так и количественный характер;
3.режим выбора может быть однократным или повторяющимся (допускает обучение
на опыте);
4.последствия выбора могут быть точно известны (выбор в условиях
определенности), иметь вероятностный характер (выбор в условиях риска) или иметь
неоднозначный исход (выбор в условиях неопределенности);
5.ответственность за выбор может быть односторонней (индивидуальной) или
многосторонней, различают индивидуальный или групповой выбор;
6.степень согласованности целей при многостороннем выборе может варьироваться
от полного совпадения интересов сторон (кооперативный выбор), до их противоположности
(выбор в конфликтной ситуации), промежуточный случай: компромиссный выбор,
коалиционный выбор, выбор в условиях нарастающего конфликта.
6.2. Метод анализа иерархий
Метод анализа иерархий (МАИ) состоит в декомпозиции проблемы на все более
простые составляющие и дальнейшей обработке последовательности суждений ЛПР. В
результате может быть выражена относительная степень (интенсивность) взаимодействия
элементов иерархии. Эти суждения затем выражаются численно. Начальными этапами МАИ
являются следующие:
1. Очертить проблему и определить цель (что хотим узнать);
2. Построить иерархию, начиная с вершины (цели), через промежуточные уровни
(критерии, по которым зависят последующие уровни) к самому нижнему уровню (который
обычно является перечнем альтернатив). Обсудим этот этап подробнее. Качество
получаемых решений практически полностью определяется тем, насколько хорошо удалось
формализовать среду задачи ПР и тем, насколько предпочтения ЛПР соотносятся с
действительностью. Математические методы получения оценок на основе качественных
могут гарантировать в (лучшем случае) лишь то, что в результате математических выкладок
не будет потерян вложенный в качественные оценки смысл. Ошибки, неточности или просто
непродуманное представление проблемы делают применение математических методов
принятия решений бессмысленным. В основе рассматриваемого метода лежит
предположение о том, что исследуемая проблема допускает декомпозицию на простые
составляющие части, которые, возможно, также могут рассматриваться как некоторая
совокупность еще более простых составляющих. При этом учитывают уровень вершин
иерархии и различают три типа вершин: вершина глобальной цели (0-левой уровень),
вершины альтернатив (последний уровень) и оставшиеся (вершины промежуточных целей).
Вершины ненулевого уровня могут интерпретироваться как задачи, решение которых
приводит к достижению целей верхнего уровня. Множество задач, которые необходимо
решить для достижения конкретной цели, задается дугами, соединяющими вершину цели с
вершинами, соответствующими задачам этого уровня. Получаемая таким образом иерархия
и заданные на основе предпочтений ЛПР меры взаимодействия вершин иерархии составляют
формализованное описание задачи ПР. В общем случае решение проблемы есть процесс
поэтапного установления приоритетов. Из опыта известны эвристические приемы и
методические рекомендации по структуризации проблемы, существуют также различные
процедуры оценки вершин иерархии.
Пример. Выпускник средней школы имеет право поступить в три университета: А, В, С.
Им сформулированы два основных критерия: местонахождение университета и его
академическая репутация (второй оценивается в пять раз выше). Приписываем веса
41
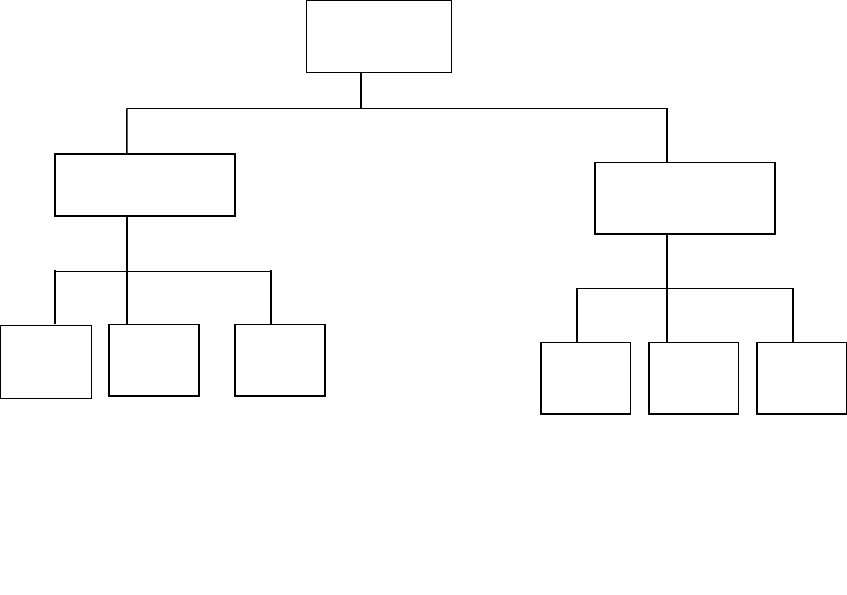
критериям 83 % (0.83) и 17 % (017). Далее произведены оценки каждого университета по
этим критериям. В итоге получается следующая иерархия.
Задачу можно усложнить. Пусть имеется брат-близнец, который также может
поступать в эти университеты (хотят учиться вместе). У него свои предпочтения
относительно критериев и альтернатив. Возникает еще один иерархический уровень.
Общий вид. Имеется иерархическое представление поставленной проблемы. Мера
взаимодействия вершин иерархии (отношение значимости (вклада, важности) решения
задачи n+1 ранга (уровня) для достижения конкретной цели n-того уровня) задается ЛПР
методом прямого назначения весов (приписыванием дугам r
n
km
иерархии (где k-номер
вершины ранга n (начало дуги), m-номер вершины ранга n+1 (конец дуги) численных
коэффициентов q
n
km
(весов)). Коэффициент q
n
km
будем называть локальным приоритетом m-
той вершины уровня n+1 относительно k-той вершины n-того уровня (X
n
k
). Пусть на n-том
уровне – C
n
вершин, а на n+1 – C
n+1
. Локальные приоритеты подчиняются следующим
соотношениям: 0
≤
n
km
q
≤
1;
1
1
1
=
∑
+
=
Cn
m
n
km
q
.
Введем вектор глобальных приоритетов (весов) вершин Х
n
k
: p
n
= (
),...,,
21
n
Cn
nn
ppp
. Для
них также: 0
≤
n
k
p
≤
1;
1
1
=
∑
=
Cn
k
n
k
p
. Решением задачи является вектор глобальных приоритетов
вершин нижнего уровня (альтернатив). Для вычисления глобальных приоритетов
используются матрицы, получившие название решающих. Столбцами матрицы Q
n,n+1
размерности C
n
×
C
n+1
являются вектора локальных приоритетов q
).,...,,(
121
n
kCn
n
k
n
k
n
k
qqq
+
=
Местоположение
0.17
Репутация
0.83
В
0.277
С
0.594
А
0.545
В
0.273
С
0.182
Комбинированные весовые коэффициенты:
Для А: 0.129*0.17+0.545*0.83=0.4753
Для В: 0.277*0.17+0.273*0.83=0.2737
Для С: 0.594*0.17+0.182*0.83=0.2520
42
Выбор
университет
а
А
0.129
Q
Cn,Cn+1
=
+++
n
CnCn
h
Cn
n
Cn
n
Cn
nn
n
Cn
nn
qqq
qqq
qqq
11211
22212
12111
..
........
..
..
.
Зная глобальные приоритеты вершин n-того уровня и имея матрицу Q
Cn,Cn+1
, можно
получить глобальные приоритеты вершин n+1 уровня: p
n+1
= Q
Cn,Cn+1
*p
n
.
Сложность метода заключается в определении локальных приоритетов. Один из
способов: использование матриц попарных сравнений. Необходимо построить множество
матриц попарного сравнения (на каждом n+1 уровне по одной матрице для каждого узла n-
того уровня). Элементы n+1 уровня сравниваются друг с другом относительно их
воздействия на элемент n-того уровня. В результате получаем квадратную матрицу суждений
A=
ij
a
. Попарные сравнения проводятся в терминах доминирования одного из элементов
над другим. Если i-тый элемент доминирует над j-тым элементом, то в клетке матрицы,
соответствующей i-той строке и j-тому столбцу, ставится целое число a
ij
. Для обеспечения
согласованности принимается, что a
ji
=1/a
ij
. Для определения матрицы суждений используют
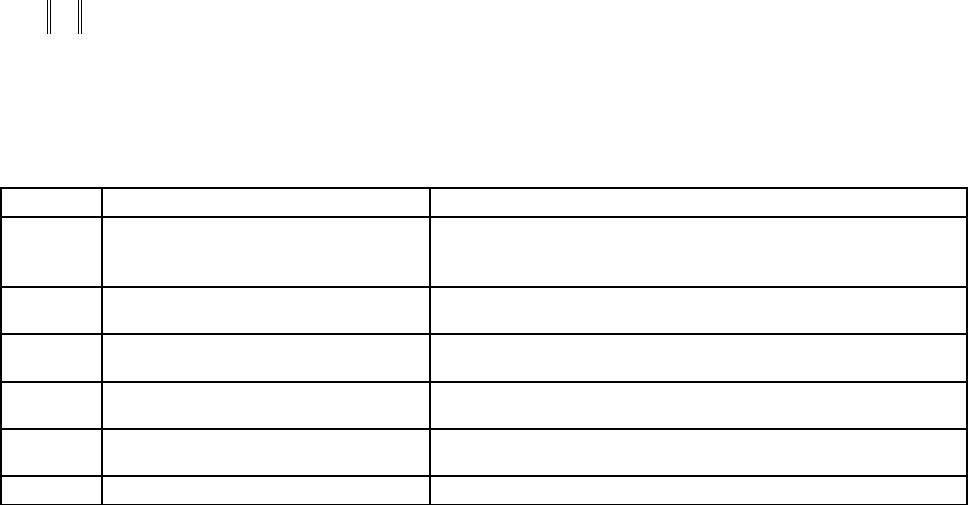
следующую девятибалльную шкалу отношений.
Баллы Определение Пояснение
1
Одинаковая значимость Оба сравниваемых элемента имеют одинаковую
значимость для элемента следующего, более высокого
уровня
3
Чуть более высокая Опыт и оценка говорят о немного большей значимости
одного элемента по сравнению с другим
5
Более высокая значимость Опыт и оценка говорят о более высокой значимости одного
элемента по сравнению с другим
7
Очень высокая значимость Очень высокая значимость элемента явно проявилась в
прошлом
9
Абсолютно доминирующая
значимость
Речь идет о максимально возможном различии между
двумя элементами
2,4,6,8
Промежуточные значения
Матрица называется согласованной, если a
ij
•
a
jk
=a
ik
. Метод анализа иерархий допускает
несогласованность суждений при попарных сравнениях как неотъемлемую часть и этим
отличается от множества подобных методов. Тем не менее, надежные решения не могут
быть приняты без приемлемого уровня согласованности и МАИ предъявляет
математический аппарат для выяснения степени надежности получаемых решений.
Соответствующие локальные приоритеты вычисляются из матрицы попарных сравнений
путем нахождения собственного вектора матрицы.
Приближенный метод. Элементы каждого столбца матрицы делятся на сумму
элементов этого же столбца (нормализация матрицы), локальные приоритеты (компоненты
собственного вектора матрицы w) вычисляются как средние значения элементов
соответствующих строк нормализованной матрицы. Для исследования уровня
согласованности матрицы необходимо найти максимальное собственное число матрицы (
max
λ
). Для этого определяется путем вычисления вектор-столбец А
w
•
(умножение матрицы
на вектор) и
max
λ
находится как сумма его элементов.
Чем ближе
max
λ
к n (ранг матрицы А), тем более согласованной является матрица А. Для
оценки уровня согласованности матрица А вычисляется отношение согласованности:
CR=CI/RI, где CI=
max
λ
- n/n – 1 - коэффициент (индекс) согласованности матрицы А,
RI=1.98
nn /)2(
−•
- стохастический коэффициент согласованности (определяется
43

эмпирическим путем как среднее значение коэффициента CI для большой выборки
генерированных случайным образом матрицы А). Если CI
1.0
≤
, уровень согласованности
является приемлемым.
Существуют и точные методы нахождения собственного вектора и собственных чисел
матрицы.
6.3. Теория статистических игр
6.3.1. Общие представления
Предмет исследования теории игр – методы принятия решений в конфликтных
ситуациях. Ситуация называется конфликтной, если в ней сталкиваются интересы
нескольких (обычно двух) лиц, преследующих противоположные цели. Экономика,
планирование военных операций, спортивные состязания, арбитражные споры, аукционы.
Большое разнообразие встречающихся на практике конфликтных ситуаций, второстепенные
привходящие факторы. Упрощенная формализованная модель конфликтной ситуации
называется игрой, а конфликтующие стороны – игроками. В дальнейшем будут
рассматриваться только игры для двух конфликтующих сторон.
Специфическим видом игр, имеющих большое значение при анализе различных
практических ситуаций, являются так называемые статистические игры. Во многих
практических ситуациях приходится сталкиваться со случаями, когда один из игроков
оказывается нейтральным, т.е. не стремиться извлечь для себя максимальной выгоды и,
следовательно, не стремится обратить в свою пользу ошибки, совершенные противником.
Природа. Под «природой» понимаем всю совокупность внешних условий, при которых
приходится принимать решение.
Неполная информация о законах природы - возможность принятия ошибочных
решений. Необходимо выработать такую стратегию в отношении принятия решений,
которая, хотя и не исключает возможность принятия неправильных решений, но сводит к
минимуму, связанные с этим нежелательные последствия.
Что считается известным в теории статистических игр? Природа. В общем случае для
природы считается заданным некоторое множество возможных состояний природы, которое
будем называть пространством состояний. Под состоянием природы будем понимать полную
совокупность внешних условий, в которых приходится принимать решение. Иногда бывает
известен не только перечень состояний природы. Из прошлого опыта бывает известно, как
часто природа принимает то или иное из своих состояний, т.е. бывает известно априорное
распределение вероятностей
)(
ϑξ
на пространстве состояний природы.
Для активной стороны (которую назовем статистиком) должны быть известны
возможные действия
l
aa ,...
1
. Множество A={
l
aa ,...
1
} назовем пространством действий
статистика. Статистик должен уметь оценить каждое из своих действий. Для этого он
допускает, что, совершая действия, он может потерпеть убыток
),(
θ
aL
- функция потерь.
Она должна быть заранее определена для всех возможных комбинаций
θϑ
∈∈
,Aa
, т.е.
должна быть задана на множестве
θ
×
A
. Её можно задать матрицей потерь
),(
...
..........
..........
...
1
111
jiij
eml
m
ij
aLq
qq
qq
qQ
θ
===
Знание функции потерь позволяет статистику предпринимать действия, которые являются
наилучшими в условиях имеющейся у него информации о состоянии природы.
44

6.3.2. Выбор в условиях риска
Статистику бывает обычно известно априорное распределение вероятности
)(
ϑξ
на
пространстве состояний природы
θ
. Это позволяет определить средние потери, которые
несет статистик, выполняя то или иное действие.
∑
∈
=
θϑ
ϑξθξ
)(),(),( aLaL
Наилучшим для статистика действием будет так называемое байесовское действие a* ,
при котором потери минимальны и равны
),(min*),()(* aLaLR
ξξξ
==
Пример 1. Задача о замене оборудования. Оборудование может быть в одном из трех
состояний:
1
ϑ
- вполне работоспособно и требует лишь небольшого текущего ремонта;
2
ϑ
- некоторые детали значительно износились и требуют серьезного ремонта или
замены;
3
ϑ
- дальнейшая эксплуатация невозможна.
Прошлый опыт показывает, что в 20% случаев оно может находиться в состоянии
1
ϑ
, в 50% -
2
ϑ
и в 30% -
3
ϑ
. Для предприятия возможны 3 различных способа действия:
а
1
- оставить оборудование в работе еще на год, проведя незначительный ремонт своими
силами;
а
2
- провести капитальный ремонт оборудования с вызовом специальной бригады
ремонтников;
а
3
- заменить оборудование новым.
Потери, которые несет предприятие при различных способах действия, приведены в
таблице. В величину потерь входит – стоимость ремонта или замены оборудования, а также
убытки, связанные с ухудшением качества продукции и с простоями, вызванными
неисправным оборудованием.
А
θ
1
θ
2
θ
3
θ
)(
ϑξ
0,2 0,5 0,3
а
1
а
2
а
3
1
3
5
5
2
4
7
6
3
Для заданного распределения вероятности
)(
ϑξ
средние потери при различных
способах действия равны:
∑
=⋅+⋅+⋅==
ϑ
ϑξθξ
8,43,075,052,01)(),(),(
11
aLaL
4,3),(
2
=
aL
ξ
9,3),(
3
=
aL
ξ
. Лучшее действие а
2
(ему соответствуют минимальные
средние потери 3,4).
6.3.3. Выбор в условиях неопределенности
Задачи принятия решения в условиях определенности. Задача выбора ассортимента
изделий, доход c
j
от изделия j считается фиксированной величиной. Если x
j
- выбранное
значение переменной, определяющее уровень выпуска изделия j, то общий вклад в доход от
изделия j, равный c
j
x
j
, является, также фиксированной величиной. Ограниченность или
45

неточность информации о задаче приводит к 2 новым типам ситуаций, в которых приходится
принимать решение:
1. в условиях риска;
2. при наличии неопределенности.
В первом случае степень неполноты данных выражается через функцию
распределения вероятности, во 2 случае существование подобных функций не
гарантируется. В условиях риска доход c
j
уже не является фиксированным. Это случайная
величина, точное цифровое значение которой неизвестно, но описывается с помощью
функции распределения f(c
j
) В условиях неопределенности f(c
j
) либо неизвестна, либо не
может быть определена. c
j
принимает одно из трех значений
jjj
ccс
′′′′′′
,,
, пока не известны
вероятности этих значений, ситуация рассматривается как принятие решений в условиях
неопределенности.
При полной определенности критерий максимума прибыли (или минимума затрат)
является почти универсальным. Напротив, для ситуаций с риском или неопределенностью
существует ряд возможных критериев. Например, в условиях риска целесообразна
максимизация ожидаемой прибыли, но встречаются случаи, когда это не верно.
В условиях неопределенности никакие вероятностные характеристики неизвестны.
Существуют различные критерии принятия решения. Основное различие между этими
критериями определяется стратегией поведения лица, принимающего решения. Не
существует общих правил применимости того или иного критерия.
Критерий Лапласа
Критерий опирается на известный принцип недостаточного обоснования. Поскольку
вероятности состояний
m
θθθ
,,
21
не известны, необходимая информация, что эти вероятности
различны отсутствует. Предполагаем, что состояния
m
θθθ
,...,
21
имеют равные вероятности.
Если так, то исходную задачу можно рассматривать как задачу принятия решения в условиях
риска, когда выбирается действие a
i
, дающее наименьший ожидаемый проигрыш, т.е. a
i
*
соответствующее
∑
=
m
j
ji
aL
m
1
),(
1
min
θ
, где 1/m – вероятность реализации состояния
).,...2,1( mj
j
=
θ
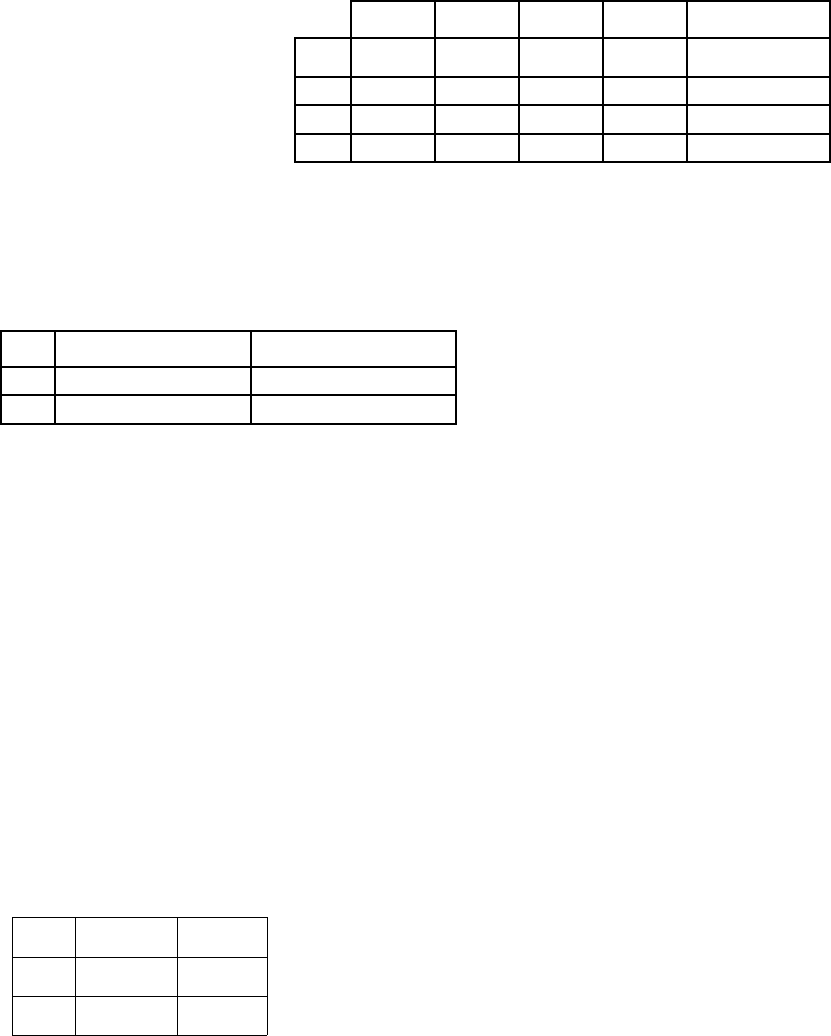
Пример 1. Одно из предприятий должно определить уровень предложений услуг так,
чтобы удовлетворить потребность клиентов в течение предстоящих праздников. Точное
число клиентов не известно, но ожидается, что оно может принять одно из четырех значений
200, 250, 300, 350 клиентов. Для каждого из этих возможных значений существует
наилучший уровень предложения (с точки зрения возможных затрат). Отклонения от этих
уровней приводят к дополнительным затратам либо из-за превышения предложения над
спросом, либо из-за неполного удовлетворения спроса. Ниже дана матрица потерь (потери в
тыс. долл.).
Принцип Лапласа предполагает, что вероятности
4
1
,,,
4321
=
θθθθ
Матрица потерь Ожидаемые средние потери:
θ
1
θ
2
θ
3
θ
4
а
1
5 10 18 25
L{a
1
}=1/4(5+10+18+25)=14,5
а
2
8 7 8 23
L{a
2
}=1/4(8+7+8+23)=11,5
а
3
21 18 12 21
L{a
3
}=1/4(21+18+12+21)=18,0
а
4
30 22 19 167
L{a
4
}=1/4(30+22+19+15)=21,5
46
Минимаксный (максиминный) критерий.
Наиболее осторожный, основывается на выборе наилучшей из наихудших возможностей.
Если результат
),(
ji
aL
θ
представляет потери лица, принимающего решение, для действия a
i
наибольшие потери независимо от возможного состояния
j
θ
будут равны
j
θ
max
{
),(
ji
aL
θ
}.
По минимаксному критерию должно выбираться действие a
i
, дающее
)},({maxmin
jia
aL
ji
θ
θ
.
Если L(
i
θ
,a
j
) выигрыш, то выбирается действие дающее
)},({minmax
jia
aL
ji
θ
θ
1
θ
2
θ
3
θ
4
θ
)},({max
ji
aL
j
θ
θ
),(
ji
aL
θ
=
a
1
5 10 18 25 25
a
2
8 7 8 23 23
a
3
21 18 12 21 21
a
4
30 22 19 15 30
21 - минимальное значение, следовательно a
3
– лучшее действие.
Критерий Сэвиджа.
Критерий минимакса слишком «пессимистичен»
1
θ
2
θ
a
1
11 000 дол. 90 дол.
a
2
10 000 дол. 10 000дол.
Minimax дает действие а
2
, но интуитивно мы склонны выбрать а
1
. Поскольку не исключено,
что
2
θθ
=
и потери составят 90 долл.
Вводится новая матрица потерь, в которой
),(
Ji
aL
θ
заменяются на
),(
ji
ar
θ
,
которые определяются следующим образом
−
−
=
)},(),({max
)},({min),(
),(
jijk
a
jk
a
ji
ji
aLaL
aLaL
ar
k
k
θθ
θθ
θ
если L – потери
если L – доход.
Это означает, что
),(
ji
ar
θ
есть разность между наилучшим значением в столбце
j
θ
и
значением
),(
ji
aL
θ
при том же
j
θ
. По существу r выражает сожаление лица, принимающего
решения, по поводу того, что он не выбрал наилучшего действия относительно состояния
j
θ
.
Функция
),(
ji
ar
θ
называется матрицей сожаления. Затем к матрице сожаления применяется
минимаксный подход. Составляем табдицу
),(
ji
ar
θ
θ
1
θ
2
a
1
1000 0
a
2
0 9910
Как и ожидалось, исходя из minmax выбираем a
1
.
47
Критерий Гурвица
Этот критерий охватывает ряд различных подходов к принятию решений: от наиболее
оптимистичного до наиболее пессимистичного. При наиболее оптимистичном подходе
можно выбрать действие, дающее
i
a
min
),(min
ji
aL
j
θ
θ
. При наиболее пессимистичных
предложениях выбираемое действие соответствует
i
a
min
),(max
ji
aL
j
θ
θ
. Критерий Гурвица
устанавливает баланс между случаями крайнего оптимизма и крайнего пессимизма
взвешиванием обоих способов поведения с соответствующими весами α и 1-α, где 0≤α≤1.
−+
)(max)1(),(minmin
jiji
a
aLaL
j
ji
θαθα
θ
θ
Параметр α определяется как показатель оптимизма: при α=1 критерий слишком
оптимистичный; при α=0 он слишком пессимистичный. Значение α между 0 и 1 может
определяться в зависимости от склонности лица, принимающего решение, к пессимизму или
оптимизму. При отсутствии ярко выраженной склонности α=1/2 представляется наиболее
разумным.
7. РАСПЛЫВЧАТОЕ (НЕЧЕТКОЕ) ОПИСАНИЕ СИТУАЦИЙ
Все известные измерительные шкалы (номинальная, порядковая, интервалов,
отношений) основаны на справедливости отношения эквивалентности. В действительности
встречаются случаи, когда тождество или различие двух состояний и/или наблюдений нельзя
утверждать с полной уверенностью. Высокий молодой человек. Довольно тяжелый сверток.
Почти каждое наше слово обозначает некоторое не вполне определенное множество.
Неопределенность смысла языковых конструкций – одна из основных трудностей
автоматизации анализа и синтеза речи. «Плоть слаба, а дух силен» → «Мясо тухлое, но водка
крепкая». Понятие лингвистической переменной – переменная, значение которой
расплывчато по своей природе, как метки размытого, расплывчатого множества.
Роль человека в современных системах управления является определяющей: он
выступает генератором целей системы и альтернативных путей её развития, определяет
реальную структуру системы и формирует её поведение. Наиболее сложным и
ответственным этапом деятельности человека в системах управления и главным фактором
всякого руководства и управления считается принятие решений. Моделирование процессов
принятия решений сегодня становится центральным направлением автоматизации
деятельности лица, принимающего решение (ЛПР). Задачи принятия сложных решений ЛПР
формирует и обсуждает на профессиональном языке, отражающем специфику задач.
Следствием этого является использование в процессе поиска наилучшего решения
качественных элементов: понятий и отношений с нечеткими границами, высказываний с
многозначной шкалой истинности. Построение моделей принятия решений для задач,
имеющих нечеткое словесное описание, оказалось возможным благодаря введению понятий
нечеткого множества и лингвистической переменной.
Объект может принадлежать к классу, описываемому данным понятием, отношением
или высказыванием, может, не относится к нему, но возможно и промежуточные градации
принадлежности. Понятия и отношения, описывающие такие классы, будем называть
нечеткими. Обобщение классического понятия множества для более корректного и полного
использования нечетких описаний процессов принятия решений привело к понятию
нечеткое множество. Теория нечетких множеств является средством формализации нечетких
понятий и отношений.
Формализация нечетких понятий и отношений профессионального языка ЛПР
обеспечивается введением понятий нечеткой и лингвистической переменной, нечеткого
множества и отношения. Первые два обеспечивают переход от словесных описаний
48
элементов задач принятия решений к числовым, другие два являются средством числового
представления нечетких понятий и отношений.
7.1. Основные понятия теории нечетких множеств. Операции над
нечеткими множествами
Нечеткое (расплывчатое) множество состоит из неопределенного числа элементов x:
признаки включения не позволяют однозначно отделить принадлежащие множеству
элементы. Некоторые элементы можно считать как относящимися к множеству, так и не
входящими в него.
Важным понятием – функция принадлежности
)(x
A
µ
. 0
≤
)(x
A
µ
≤
1 выражает степень
принадлежности:
)(x
A
µ
=0;
)(x
A
µ
=1 – крайние градации (непринадлежность, полная
принадлежность). Может быть частичная принадлежность.
Нечетким множеством называется совокупность упорядоченных пар A={(x,
)(x
Xx
A
∈
µ
}
Функция
)(x
A
µ
задается как отображение универсального множества x на отрезок [0,1]
Форма записи
.
)(
...
)(
1
1
n
n
x
x
x
x
A
µµ
++=
(+ - знак объединение) или
∫
∈
=
Xx
A
x
x
A
)(
µ
, если
)(x
A
µ
непрерывная функция от x.
Носитель нечеткого множества:
}0)({
>∈=
xXxS
AA
µ
Небольшой запас деталей на складе:
40
1,0
...
33
8,0
32
9,0
31
0,1
...
29
0,1
...
20
0,1
19
9,0
...
12
2,0
11
1,0
10
05,0
+++++++++++++=
А
Значение функции принадлежности
)(x
A
µ
для элемента x
∈
X будем называть степенью
принадлежности. Интерпретацией степени принадлежности
)(x
A
µ
является субъектная
мера того, насколько элемент x
∈
X соответствует понятию, смысл которого формализуется
нечетким множеством А.
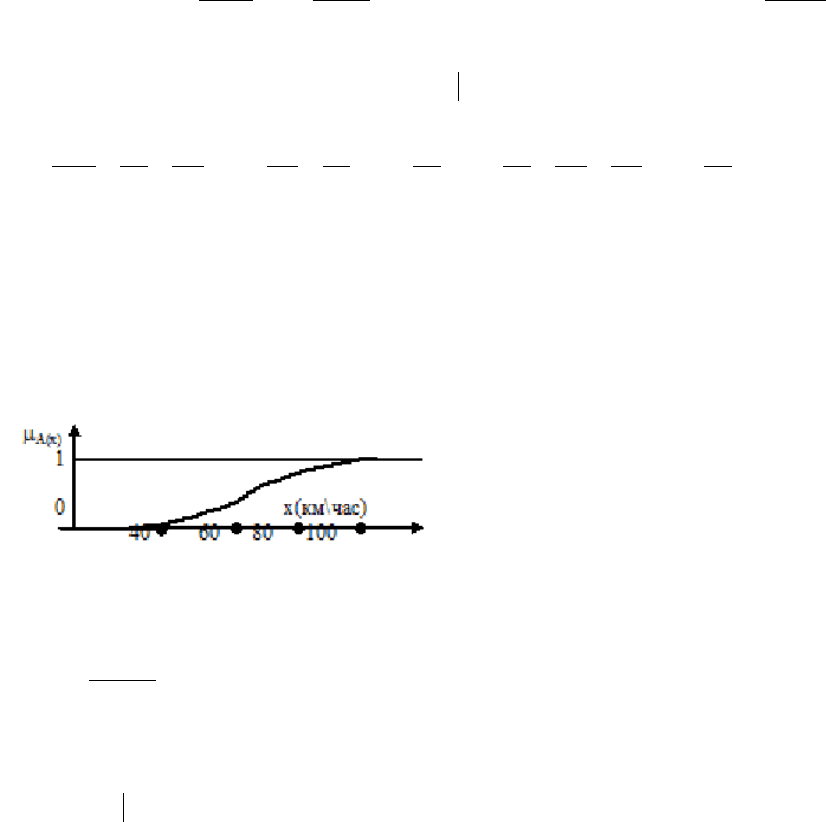
Высокая скорость автомобиля: Нечеткое множество называется
нормальным, если верхняя граница
принадлежности равна 1
1)(
=
∈
xSup
A
Xx
µ
Если
1)(sup
<
∈
x
A
Xx
µ
, то множество
называется субнормальным.
Пустое множество:
0)(
=
x
A
µ
.
Непустое субнормальное множество можно привести к нормальному виду:
Xx
A
A
A
x
x
∈
=
µ
µ
µ
sup
)(
)(
Множеством уровня α нечеткого множества А называется четкое подмножество
универсального множества Х:
{ }
αµ
α
≥∈=
)(xXxA
A
α∈[0,1]
49

Операции над нечеткими множествами:
Равенство множеств А и В:
XxxxBA
BA
∈∀=⇔=
))()(()(
µµ
.
Включение нечеткого множества А в
множество В:
[ ]
XxxxBA
BA
∈∀≤⇔⊆
)()()(
µµ
(очень большие числа ⊆ большие числа).
Дополнение: A
′
называется дополнением к
)(1)( xxA
AA
µµ
−=⇔
′
Высокие люди – невысокие люди могут являться дополнением (при
соответствующем определении) (соответствует логическому отрицанию).
Пересечение :
[ ]
XxxxxBA
BABA
∈∀=⇔
)(),(min)(
µµµ
(соответствует логической связке
«и»).
Объединение:
[ ]
XxxxxBA
BABA
∈∀=⇔
)(),(max)(
µµµ
(соответствует логической связке
«или»).
Удобно определить составные множества, которые соответствуют конкретным
арифметическим операциям над
i
µ
. Алгебраическое произведение множеств АВ:
Xxxxx
BAAB
∈∀⋅=
),()()(
µµµ
.
Алгебраическая сумма
BA
⊕
:
Xxxxxxx
BABABA
∈∀⋅−+=
⊕
),()()()()(
µµµµµ
.
Нечеткие отношения
Отношения могут быть заданы перечислением всех пар (u
i
,u
j
)
∈
U
×
U, для которых
выполняется отношение R: u
1
R u
2
(отношение R на множестве U).
Четкие отношения:
=
ji
ji
ij
uRuесли
Ruuесли
Ra
:,0
:,1
)(
Нечеткое отношение R определяется как нечеткое подмножество
UU
×
, т. е.
UUR
×⊆
R- отношение «близко к»
∫
×∈
=
2121
),(
21
21
),(
),(
UUuu
R
uu
uu
R
µ
∫
×∈
−−
=
,
),(
21
)
2
,
1
(
21
21
UUuu
uu
uu
eR
α
Нечеткое отношение – это нечеткое множество с векторной базовой переменной.
7.2. Понятие лингвистической переменной (ЛП)
Отличие от численной переменной – её значениями являются не числа, а слова,
предложения на естественном или формальном языках. Лингвистическое описание менее
точное, чем количественное, тем не менее дает возможность приближенно описывать
явления довольно сложные и не поддающиеся описанию в количественных переменных.
ЛП – понятие более высокого порядка, чем нечеткая переменная. Значениями ЛП
являются нечеткие переменные (НП).
Определение ЛП:
MGUTX ,,,,
Х- наименование ЛП;
50
