Лекции - Плоское течение идеальной несжимаемой жидкости
Подождите немного. Документ загружается.

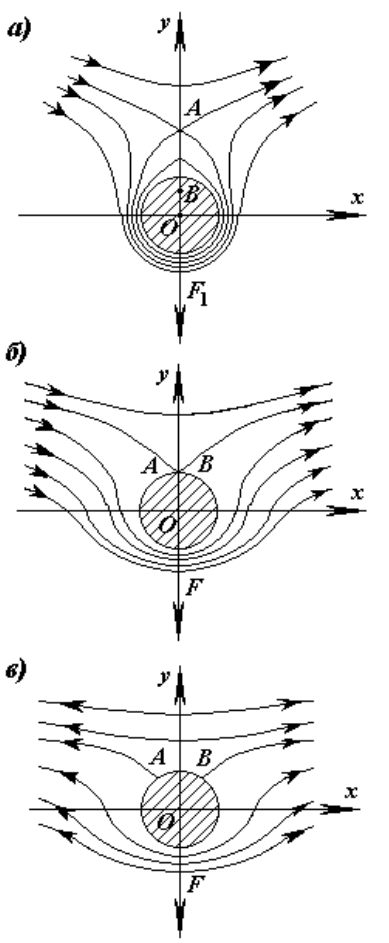
Рисунок 12.8 - Циркуляционное обтекание цилиндра
вычитаются. Поэтому, согласно уравнению Бернулли, под цилиндром (где
скорости больше) давление меньше, а над цилиндром больше, т.е. цилиндр
будет выталкиваться вниз с некоторой силой F.
Если изменить направление циркуляции (по часовой стрелке (Г< 0),
картина обтекания перевернется на 180
0
вокруг оси ОХ и сила F будет
действовать вверх по оси ОУ. Итак, если поместить начало вектора w
o
в
21

центр цилиндра о, повернуть его на 90
0
против циркуляционного движения
жидкости, получим направление вектора F.
Из соображений симметрии следует, что х = 0, т. е . сила сопротивления
вдоль направления w
отсутствует.
Вычисление F
y
= F дает:
2
F= F
y
=
a
2
(2w
sin Г/2a)
2
sin d = - w
Г (12.24)
0
Таким образом, как и при бесциркуляционном обтекании, при
циркуляции сила сопротивления в направлении w
o
отсутствует, но возникает
поперечная сила F
y
(перпендикулярная w
o
), равная произведению плотности
жидкости набегающего потока w
o
на циркуляцию Г:
F
у
=F = - w
Г *
)
[Н/м]. (12.24
1
)
Полученное выражение (12.24), (12.24
1
) для F
y
является частным случаем
общей теоремы Жуковского, относящейся к любому обтекаемому контуру.
12.5 Общие особенности обтекания тел идеальной жидкостью
Вдали от обтекаемого тела (любой формы) поток жидкости **
)
можно
считать невозмущенным, однородным, движущимся со скоростью w
в
направлении оси Х и давлением p
. Тогда для любой струйки тока,
начинающейся "на бесконечности", где и не сказывается влияние обтекаемого
_________________________
*
)
При вращении цилиндра в потоке реальной (вязкой) жидкости можно наблюдать
возникновение циркуляционного движения, качественно похожего на рассмотренное.
Эффект образования при этом поперечной силы получил название эффекта Магнуса (1852).
**
)
Для простоты всюду, где это не оговорено, поток будем считать плоским,
движущемся параллельно плоскости [x,y].
тела, и для некоторой точки на поверхности тела, где скорость w и давление p,
можно написать уравнение Бернулли
22
w
2
/2 + р
= w
2
/2 + p, (12.25)
или, вводя число Эйлера - коэффициент давления
p
(см. (12.20)):
p
= (p - р
) / ( w
2
/ 2) = 1 - w
2
/ w
2
.
На поверхности тела коэффициент давления определяется, таким
образом, относительной скоростью w/w
- возмущающим воздействием
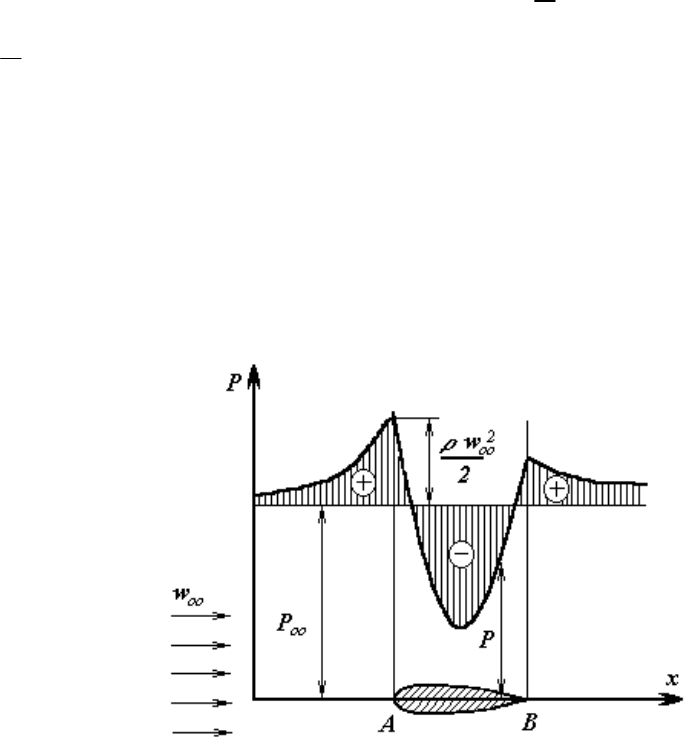
обтекаемого тела на набегающий поток, рисунок 12.9. В передней критической
точке А заторможенный набегающий поток раздваивается.
Рисунок 12.9 - Распределение давлений при обтеканиии тела
Благодаря торможению давление в точке А достигает максимума, равного (р
+ w
2
/2). В области утолщения обтекаемого тела скорость w превосходит
w
, а разрежение нарастает (р < p
) вплоть до максимального утолщения
тела (до "миделя"). В капельной жидкости в этом сечении наиболее вероятно
возникновение кавитации (при понижении р до давления насыщенного пара). В
кормовой части (за "миделем") разрежение уменьшается (давление
"восстанавливается"), а скорость w уменьшается, стремясь к w
. До миделя
течение называют конфузорным, за миделем - диффузорным.
При обтекании тела без отрыва потока идеальной жидкостью
возрастание давления в диффузорной части полностью компенсирует его
23

понижение в конфузорной. Поэтому равнодействующая сил давления на тело в
направлении потока ( в направлении оси Х) равна нулю (парадокс Деламбера).
На самом деле в реальной (вязкой) жидкости даже при безотрывном
обтекании существует сила вязкого сопротивления (в направлении оси Х). При
этом в диффузорной части течения наиболее вероятен отрыв потока от стенки и
образование вихревой зоны, резко увеличивающей силу сопротивления (и
уменьшающий подъемную силу - по направлению оси У).
Теорема Жуковского (для идеальной жидкости), как уже отмечалось
выше, для частного случая обтекания цилиндра с циркуляцией, как раз и
устанавливает величину (подъемной) силы в направлении ОУ,
перпендикулярном скорости набегающего потока w
.
Докажем справедливость формулы (12.24) и (12.24
1
) для любого
обтекаемого тела (рисунок 12.10) потоком идеальной жидкости. Вблизи тела
течение оказывается заметно возмущенным; появляются "добавки" к скорости
w
, которые обозначим w
x
/
; w
y
/
. Тогда величина скорости для каждой точки,
куда распространяются возмущения от тела, подставится в виде
w =
22
yx
www
.
при удалении от тела, очевидно, w
x
/
0, w
y
/
0.
Применим для определения F
y
уравнение количества движения (см. гл.
4).
Выберем контрольную поверхность АВСD в виде прямоугольника,
расположенную на таком расстоянии от тела, что w
x
/
и w
y
/
малы по сравнению
с w
и квадратами их можно пренебречь, рисунок 12.10.
24
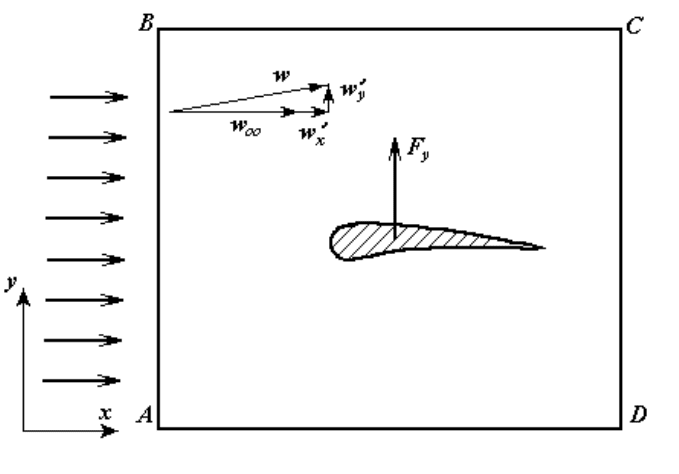
Рисунок 12.10 - К доказательству теоремы Н. Е. Жуковского
Тогда количеством движения, передаваемым через ВС и АD, можно
пренебречь вследствие малости w
y
/
. Следовательно, подсчитав разность между
количеством движения в направлении ОУ, поступающим через АВ и уходящим
через СD, можно определить сумму всех сил, действующих в направлении ОУ
на поверхность АВСD. Эта сумма складывается из сил давления на АD и ВС,
которые обозначим через Р, и из силы F
y
, действующей на тело.
Количество движения, входящее через АВ (в слое единичной толщины в
направлении, перпендикулярном рисунку) в направлении ОУ, равно
B
(w
+ w
x
/
) w
y
/
dy,
A
а выходящее через DС
C
(w
+ w
x
/
) w
y
/
dy.
D
Для подсчета силы давления
D C
P = pdx - pdx
A B
25
используем уравнение Бернулли (12.25). Входящий в него квадрат скорости w,
можно представить в виде (пренебрегая квадратом возмущений):
w
2
= (w
+ w
x
/
)
2
+ (w
y
/
)2 w
2
+ 2w
w
x
/
.
Тогда из (12.25) следует
p - p
/2 (w
2
- w
2
- 2w
w
x
/
) = - w
w
x
/
.
Поскольку р
= const (давление вдали от тела в невозмущенном
однородном потоке), его можно принять равным нулю (т. к. оно все равно дает
на замкнутой поверхности результирующую, равную нулю). Тогда сила F
y
,
равная разности приращения количества движения и силы давления Р,
определяется выражением:
B C
F
y
= - (w
+ w
x
/
) w
y
/
dy + (w
+ w
x
/
) w
y
/
dy +
A D
D C
+ w
w
x
/
dx - w
w
x
/
dx.
A B
Или, пренебрегая слагаемыми второго порядка малости вида w
x
/
w
y
/
dy,
получим:
B D A C
F
y
= w
(- w
y
/
dy - w
y
/
dy - w
x
/
dx - w
x
/
dx).
A C D B
Но сумма интегралов в скобках представляет собой циркуляцию
добавочной скорости по контуру АВСD. Таким образом, и в общем случае
произвольной формы тела приходим к формуле (12.24
1
) (Жуковский Н. Е.,
1906):
F
y
= w
Г [Н/м] :
- поперечная сила, действующая на обтекаемое плоским потоком тело
единичной толщины, пропорциональна плотности, скорости набегающего
потока и циркуляции по контуру , охватывающему тело.
26
Если протяженность тела в направлении, перпендикулярном плоскости
[x, y] , равна l, то
F
y
= w
Г l [Н] .
Например, l - размах крыла [м].
Теорема Н. Е Жуковского имеет основополагающее значение для теории
крыла. Под "крылом" подразумевается не только несущая плоскость самолета
или судна на подводных крыльях, но и лопасти пропеллера, гребного винта,
фальшкиль и перо руля яхты, лопатки турбины и компрессора или насоса -
вообще тело с плавными отводами и заостренной задней кромкой, обтекаемое
продольно или под небольшим углом атаки без отрыва потока.
Возникновение циркуляции при обтекании крылового профиля связано с
тем, что за задней острой кромкой формируется поверхность разрыва
скоростей верхней и нижней частей потока, рисунок 12.11, сворачивающаяся в
вихрь. Вихрь увлекается внешним потоком. При сносе вихря определенной
интенсивности около профиля сохраняется вихрь, равный по интенсивности, но
противоположный по направлению вращения. В этом состоит содержание
постулата С. А. Чаплыгина и Н. Е. Жуковского: при безотрывном обтекании
профиля вокруг него формируется такая циркуляция Г, которая обеспечивает
сход струек с задней кромки вдоль средней линии профиля.
В этом смысле крыло можно рассматривать как несущую вихревую линию.
Так как скорости, генерируемые вихревой линией, убывают 1/r (где r -
расстояние от вихревой линии). т. е.
w
/
Г/ 2r.
на удалении от профиля картина течения представляется такой же, как если бы
крыло заменить вихревой линией. При этом ядро вихря, т. е. его внутренняя
область, где жидкость должна вращаться как твердое тело, размещается внутри
крыла.
27
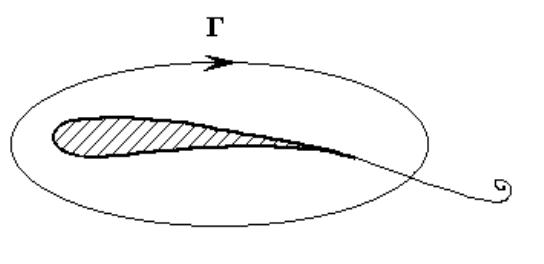
Рисунок 12.11 - Возникновение вихря за задней острой кромкой крыла
28
