Лекции - Основы промышленной безопасности
Подождите немного. Документ загружается.

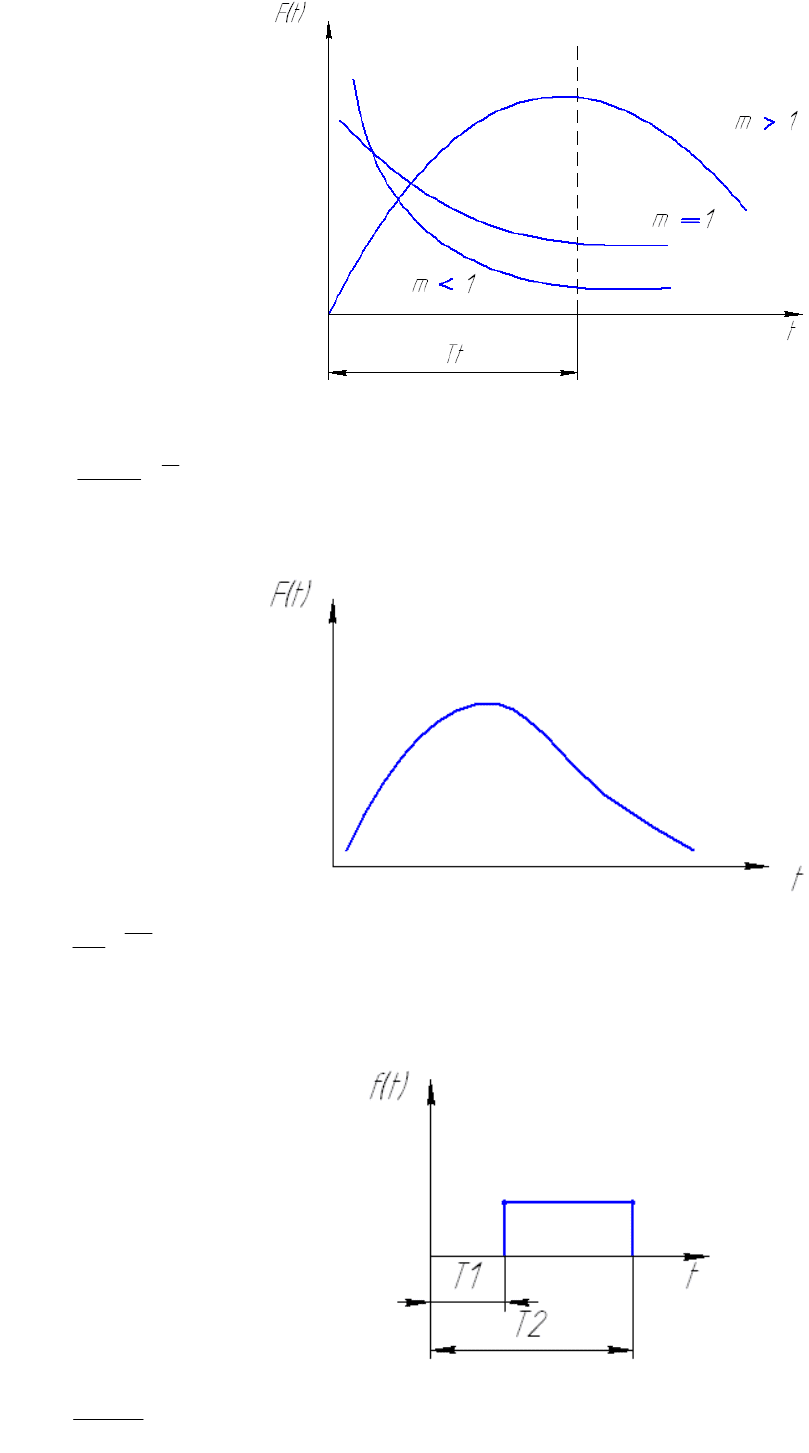
e
T
t
m
m
T
mt
tf
1
1
1
)(
6)Закон Релея
e
t
t
tf
2
2
2
2
)(
7)Закон равномерного распределения.
12
1
)(
TT
tf
при
21
TtT
Лекция 10
Алгоритмы расчёта характеристик надёжности элементов Т,С,
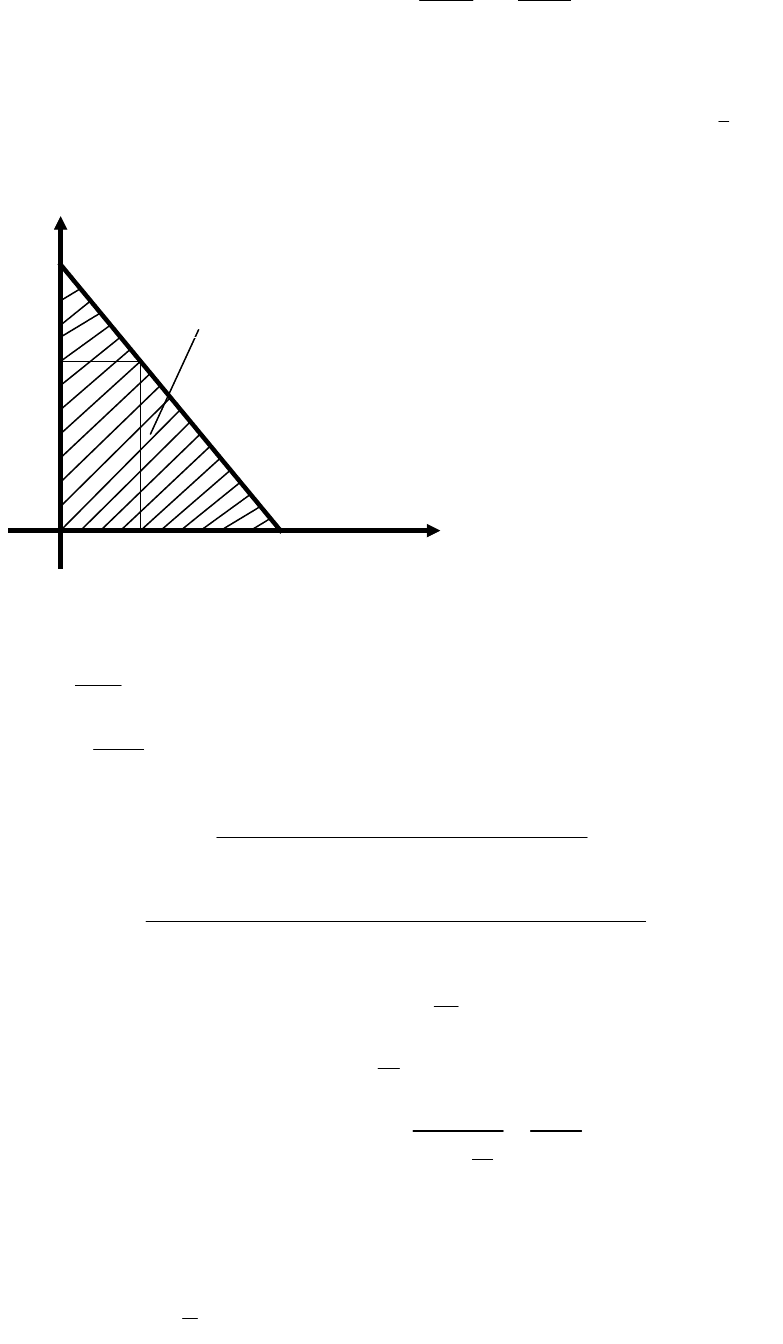
с использованием функций кривых распределения.
Напомним известные соотношения для интенсивности отказов и вероятности безотказной работы
)(
)(
)(
)(
)(
tQ
tQ
tQ
tF
t
;
1 – F(t) = Q(t) .
Пример 1. Надёжность элемента убывает со временем по линейному закону (рис. 1а). Найти
интенсивность отказов
)(t
и среднее время безотказной работы элемента
t
.
Решение.
а) на участке (
,0
0
t
)
Рис. 1 а
имеем
)(
)(
)(
)(
)(
)(
tq
tq
t
tq
t
t
;
1)
работыйбезотказноьВероятност
отказовФункция
2)
работыйбезотказноьВероятност
работыйбезотказноьвероятностяПроизводна
Согласно заданному на рис. 1а закону надёжности имеем:
q(t)=1-
0
t
t
)0(
0
tt
Тогда
0
1
)(
t
tq
и
tt
t
t
t
t
0
0
0
1
)1(
1
)(
.
В итоге с увеличением t уменьшается
tt
0
и это ведет к увеличению
)(t
График функции
)(t
показан на рис. 1. б. При
0
tt
)(t
.
б) Среднее время безотказной работы равно площади, ограниченной кривой q(t) и осями
координат (см. рис. 1а):
t
.2/
0
t
=S=
q(t)
Вероятность
безотказной работы
0
Х
1
t
0
t
t
t

Рис. 1 б
где
t
- среднее время безотказной работы
Величина
t
равна площади, ограниченной кривой q(t) и осями координат. Применим для
определения
t
метод интегрирования.
t
dt
t
t
t
0
0
0
1
=
.
222
2
2
11
0
0
2
0
0
2
0
2
0
2
0
0
0
0
0
0
00
t
t
t
t
ttt
t
tdt
t
dt
tt
В итоге, как и ранее, имеем:
.
0
0
2
1
2
1
ABC
S
t
tt
Пример 2. Распределение времени отказов элемента постоянно на участке (
),(
01
tt
и равно нулю вне
этого участка (рис. 2а). Найти интенсивность отказов
).(t
Решение. Как и ранее в примере 1, для участка
10
...tt
имеем:
)(1
)(
)(
)(
)(
tp
t
tq
t
t
),(
10
ttt
Т.е. как и в примере 1 величина
).(t
определяется отношением функции отказов к вероятности
безотказной работы
Вероятность отказов найдем методом интегрирования функции отказов
).(t
p(t) =
dtt
t
t
1
0
)(
.
p(t) =
01
0
01
0
1
tt
tt
dt
tt
t
t
.
В итоге:
)(t
0
1
t
0
t
t
0
A
B
0
1
q(t)
t
0
t
t
0
t
0
t
0
t
0

tt
t
1
1
)(
при
01
1
)(
tt
t
График интенсивности отказов показан на рис. 2б: при t
1
t
)(t
.
Рис. 2 а Рис. 2 б
Покажем интегрированные выше при определении
).(t
преобразования.
t
t
tt
tP
0
01
1
)(
=
01
tt
t
01
0
01
0
01
0
tt
tt
tt
t
tt
t
t
t
.
01
1
01
001
01
0
1)(1)(
tt
tt
tt
tttt
tt
tt
tptq
.
01
1
01
1
)(
tt
tt
tt
t
tt
1
1
.
В итоге при
1
tt
)(t
(рис. 2б)
Пример 3. В теории надёжности технической системы надёжность элемента или системы принято
характеризовать средней интенсивностью отказов
).(t
Она представляет собой функцию времени,
которая будучи умноженная на dt, даёт условную вероятность отказа элемента в интервале времени (
1
t
)dtt
в предположении, что до момента t элемент работал исправно. Зная функцию
)(t
, можно
найти закон плотности распределения срока службы элемента
).(tf
При этом выделяют два события:
А – исправную работу элемента до момента t,
B – отказ элемента в интервале времени (
).; dttt
Очевидно следует исходить из того, что событие В может произойти только вместе с событием А.
Поэтому Р(В)=Р(АВ),
где: Р(АВ) – вероятность совместного появления события А и В.
В то же время на основе принципа умножения вероятностей можно записать:
Р(В)=Р(А)∙Р(В/А)
*)
Обозначим неизвестные функции распределения плотности вероятности срока службы элемента,
соответственно через F
(t)
и f
(t)
.
Тогда вероятность события (В) – отказа можно записать
Р(В)=Р(Т<t) или Р(В)=Р(t<Т<t+dt) = f
(t)
dt=F
'
(t)
dt.
Вероятность события А (безотказной) работы через функцию распределения срока службы элемента
Р(А)=Р
(Т≥t)
=1-Р
(Т<t)
= 1-F
(t)
.
И, наконец, условную вероятность Р(В/А) можно выразить через среднюю интенсивность отказов
элемента λ
(t)
Р(В/А)= λ
(t)
dt.
Подставляя полученные выражения в *) получим соотношение F
'
(t)
dt = [1-F(t)] λ
(t)
, которое
представляет собой дифференциальное уравнение.
0
01
1
tt
0
t
1
t
t
)(t
0
1
1
t
)(t
0
t
1
t
t

Так как срок службы элемента не может быть отрицательным, то событие Т<0 невозможно и,
следовательно, F
(0)
=0.
Интегрируя дифференциальное уравнение при начальном условии F
(0)
=0, найдём функцию
распределения срока службы элемента
F
(t)
=1-exp(-
t
t
0
)(
dt)
И соответственно
t
dttttf
0
)(exp)()(
.
В частном случае при постоянной интенсивности отказов λ
(t)
=λ формулы F
(t)
и f
(t)
принимают вид
F
(t)
=1-e
-λt
: f
(t)
=λe
-λt
Таким образом при постоянной интенсивности отказов λ срок службы элемента подчинен
показательному закону распределения.
Пример 4. Поиск условной вероятности отказа элемента в интервале времени (t
1
…t
2
) в
предположении, что он исправно работал до момента t
1
.
Рассмотрим 2 события:
А – исправная работа элемента до момента t
1,
B – отказ элемента в интервале времени (t
1
…t
2
).
Используя базовые соотношения теории вероятности и приведенные ранее формулы запишем
P(B)=P(t
1
<T<t
2
)=
)()(
12
tt
FF
,
P(A)=P(T≥t
1
)=1-P(T<t
1
)=1-
)(
1
t
F
Для определения искомой вероятности отказа элемента в интервале времени (t
1
…t
2
) при условии,
что до t
1
он работал неправильно воспользуемся известным соотношением
P(AB)=P(A)∙P(B/A).
Откуда при условии, что событие В появляется только вместе с событием А получим
)(
)()(
1
21
1)(
)(
)(
)(
)/(
t
tt
F
FF
AP
BP
AP
ABP
ABP
.
Производя замену F
(t)
по зависимостям, полученным ранее, имеем:
2
1
)(
exp1)/(
t
t
t
dtABP
.
Имея своей целью преобразование соотношения для определения P(B), используем формулу
F
(t)
=1-
)(t
e
, тогда P(B) =
)
1
(t
e
-
)
2
(t
e
.
Дальнейшие преобразования приводят к:
P(A) =
)
1
(t
e
;
)(
12
)
1
()
2
(
)
1
(
)
2
()
1
(
11)/(
tt
ee
e
ee
ABP
tt
t
tt
;
где
)/( ABP
- условная вероятность отказа элемента в интервале времени (t
1
…t
2
) при условии, что до
момента t
1
элемент работал исправно.
Пример 5. Интенсивность отказов элемента
)(t
меняется по закону, представленному на рис. 3 а.
Найти закон надёжности q(t).
Решение. Найдём q(t) на участке (0,1), т.е при t = 0…1 и
.23)( tt
Так как
kxbt )(
, то на участке (0…1) имеем
.23)( tt
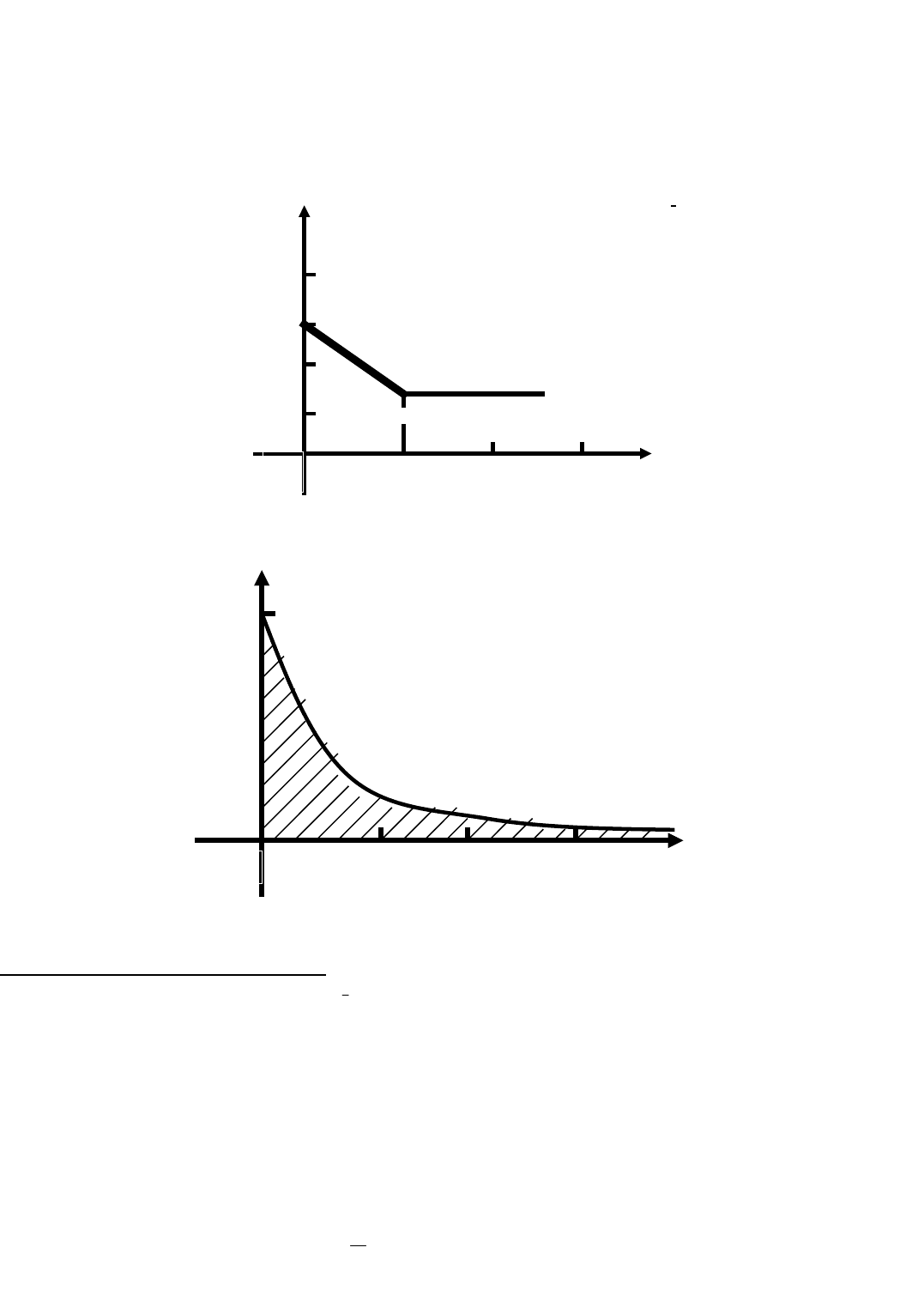
Тогда в соответствии с зависимостью
t
dtt
etq
0
)(
)(
получим
)3(
2
)(
tt
etq
.
Вычислим q(t) при t>1. В общей формуле разобьём промежуток интегрирования на два: от 0 до 1 и от 1
до t:
Тогда
tt t
ttdtdttdttdttdtt
10
1
0 1
1
0
;1121)23()()()(
В результате общее соотношение для
)(tq
на участке (0…t) будет иметь вид
)1(
)(
t
etq
Рис. 3 а
Рис. 3 б
График закона надёжности
)()( tftq
показан на рисунке 3 б. Заштрихованная площадь изображает
среднее время безотказной работы. Его найдем суммированием по двум участкам: 0…1 и 2…∞
.
1
)1(
1
0
)3(
dtedtet
ttt
Второй интеграл здесь равен
∞
)1( t
e
│
.135,0
2
e
1
Что касается первого, то он может быть вычислен приближённо (численно):
370,0
1
0
)3(
2
dte
tt
,
Откуда общая величина среднего времени безотказной работы будет равна
.505,0135,0370,0 t
Лекция 11.
4
3
2
1
0
1 2 t
q(t)
1,0
0 1 2 t
Вероятность безотказной работы

Расчёт характеристик надёжности ТС.
1.Технические системы без резервирования.
Самым простым случаем в расчётном смысле является система с последовательным
соединением элементов (без резервирования). В такой системе отказ любого элемента равносилен
отказу системы в целом. Представим схему такой Т.С. в виде
цепочки элементов.
Обозначим надёжности элементов нерезервированной системы
как q
1
, q
2
,…, q
i
. Предположим, что элементы отказывают независимо друг от друга. Тогда по правилу
умножения вероятностей независимых событий надёжность нерезервированной системы
q = q
1
q
2
… q
i
=
n
i 1
qi.
То есть надежность системы ,составленной из независимых последовательно соединенных
элементов ,равна произведению надежностей её элементов. Это говорит о том ,что увеличении числа
элементов резко падает надежность всей системы.
Пример 1
Надёжность систем без резервирования
Система состоит из 10 независимых элементов, надёжность каждого из которых равна q=0,95.
Надёжность всей системы: q = 0,95
10
0,6
2. Интенсивность отказов системы.
Интенсивность отказов нерезервированной системы равна сумме интенсивностей отказов
элементов системы
n
1i
i
)t()t(
.
Пример
Простая система состоит из трёх независимых элементов, для которых плотности распределения
вероятности отказной работы представлены на рис.
Найти интенсивность отказов системы.
1) Запишем (примем из рис.) ненадёжность
каждого элемента (вероятность отказа).
P1(t) = t; P
2
(t) = t
2
; P
3
(t) = 2t - t
2
.
2) Определим надёжность элементов.
q
1
(t) =1-t; q
2
(t) = 1-t
2
; q
3
(t) = 1 – 2t + t
2
.
3) Интенсивности отказов элементов.
ttq
tq
t
1
1'
1
;
2
2
t1
t2
)t(
;
t1
2
tt21
)t1(2
)t(
2
3
.
4) Интенсивность отказов системы.
22
321
t1
t53
t1
2
t1
t2
t1
1
)t(λ)t(λ)t(λ)t(Λ
2.Технические системы с резервированием.
Эффективным методом повышения надёжности системы является
введение в неё дублирующих (резервных) элементов. Резервные элементы
включаются в систему, например как параллельные тем, надёжность которых
недостаточна. При параллельном соединении элементов отказ системы
p
1
p
2
p
n
p
1
p
2
p
n

происходит лишь при отказе всех входящих в неё элементов. Примером резервирования может служить
устройство для выпуска шасси самолёта (основным и аварийным способом) и т.д.
Схемы резервирования системы выполняют по способам общего или раздельного
резервирования. Общее резервирование – это резервирование системы в целом, а раздельное – по
отдельным участкам (блокам) или элементам системы. В зависимости от масштабов раздельного
резервирования разделяют групповое, поэлементное или внутреннее резервирование (увеличение запаса
прочности).
По методу включения резерва различают активное и пассивное резервирование. Под активным
резервированием подразумевают наличие автоматических или неавтоматических устройств,
осуществляющих включение резерва при выходе из строя изделия или основных элементов. При
пассивном резервировании резерв включён постоянно и работает наравне с основным элементом.
Рассмотрим схему параллельного включения элементов (см. рис.).
Это самый простой пример резервированной системы, когда содержится несколько
"параллельно" включенных элементов. Вначале работает "основной" элемент q
1
. В случае его отказа
система переключается на "резервный". При этом все элементы держатся под так называемым рабочим
напряжением (работают наравне с основным элементом). Предполагается, что все элементы
независимы по отказам и надёжности их безотказной работы за определённое время равны.
По правилу умножения вероятностей независимых событий-отказов имеем:
P = p
1
p
2
… p
n
,
где P – вероятность отказа системы; p
i
– вероятность отказа i-го элемента.
Перепишем…
1 – q = (1 – q
1
) (1 – q
2
) … (1 – q
n
).
q = 1 – (1 – q
1
) (1 – q
2
) … (1 – q
n
).
q = 1 – (1 – q
i
)
n
.
Если надёжности элементов различны, то это выражение принимает вид
n
i
i
qq
1
11
.
При расчёте надёжности системы, в которой применяются как "последовательное", так и
"параллельное" резервирование, её разделяют на ряд подсистем которые можно охарактеризовать
одним способом соединения.
Пример.
То есть надёжность системы, составленной из независимых
последовательно соединённых элементов, равна произведению
надёжностей её элементов. Это говорит о том, что при увеличении числа
элементов резко падает надёжность всей системы.
Определить надёжность системы с надёжностями q
1
, q
2
, …, p
7
.
Для подсистемы I: q
I
= q
1
q
2
.
Для подсистемы II: q
II
= 1 – (1 – q
3
) (1 – q
4
).
Для подсистемы III: q
III
= q
I
q
II
.
Для подсистемы IV: q
IV
= 1 – (1 – q
6
) (1 – q
7
).
Для подсистемы V: q
V
= q
5
q
IV
.
Для подсистемы V: q = 1 – (1 – q
III
) (1 – q
V
).
Холодный (облегчённый) резерв (активное резервирование)
При таком соединении резервный элемент включается в работу системы только при отказе
основного элемента и, в связи с этим, не имел отказов при работе системы (холодный резерв), или же
имел отказы с меньшей плотностью вероятности, чем у основного элемента (облегчённый).
Рассмотрим случай холодного резервирования в системе при условии простейшего потока
отказов элементов.
Система состоит из основного элемента p
1
и двух резервных p
2
и p
3
. При отказе элемента p
1
в
работу включается элемент p
2
, при отказе элемента p
2
– p
3
. До включения каждый из резервных
элементов находится в "холодном" резерве и отказать не может. Интенсивность потока отказов
основного элемента
1
; интенсивность потока отказов каждого из резервных элементов при работе
равна
2
.
p
1
p
3
p
2
p
4
p
6
p
7
p
5
I II
III
IV
V
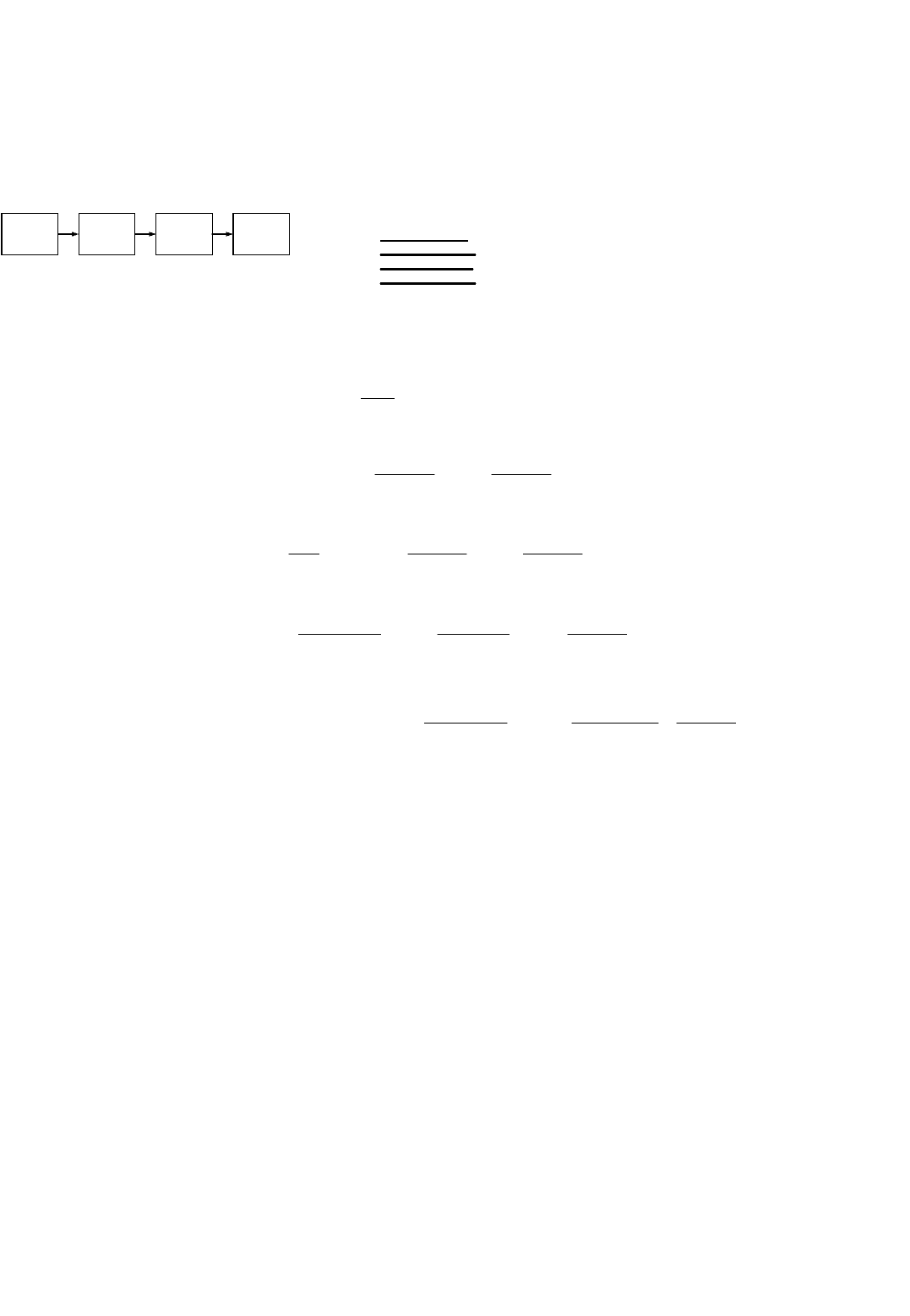
Для определения надёжности системы процесс работы системы рассматривается как процесс с
дискретными состояниями и непрерывным временем (марковский процесс). Для данной системы
возможны четыре состояния:
S
1
– работает основной элемент p
1
;
S
2
– работает резервный элемент p
2
;
S
3
– работает резервный элемент p
3
;
S
4
– не работает ни один элемент.
Последовательность событий представлена на графе состояний системы.
Для определения вероятностей состояний системы применяется
система уравнений Колмогорова:
32
4
2232
3
1122
2
11
1
p
dt
dp
pp
dt
dp
pp
dt
dp
p
dt
dp
После интегрирования при начальном условии p
1
(0) = 1
t
1
1
e)t(p
.
Полученное значение p
1
(t) во второе уравнение системы:
t
122
2
1
ep
dt
dp
.
После интегрирования этого выражения при начальном условии p
2
(0) = 0
t
12
1
t
12
1
2
21
ee)t(p
.
Эту функцию подставляют в третье уравнение
t
12
21
t
12
21
32
3
21
eep
dt
dp
Это уравнение также интегрируется при начальном условии p
3
(0) = 0:
t
12
21
t
12
21
t
2
12
21
3
221
e
t
e
)(
e
)(
)t(p
.
Функцию p
4
(t) можно найти из условия, что p
1
(t) + p
2
(t) + p
3
(t) + p
4
(t) = 0:
p
4
(t) = 1 – (p
1
(t) + p
2
(t) + p
3
(t)) = 1 –
t
12
21
2
12
21
2
1
t
2
12
2
2
21
e
t
)(
2
e
)(
.
Схемы марковских случайных процессов.
Для описания случайных процессов, происходящих в технических системах, применяется
математический аппарат, разработанный в теории вероятностей для так называемых марковских
случайных процессов.
В практике часто встречаются случайные процессы, которые с той или иной степенью
приближения можно считать марковскими (описание физических явлений типа диффузии; процессы
распространения мутаций; процессы образования очередей).
Марковские случайные процессы делятся на классы в зависимости от того как и в какие моменты
времени система может менять свои состояния. Различают процессы
· с дискретными состояниями, если возможные состояния системы можно перечислить, а сам процесс
состоит в том, что время от времени система скачком (мгновенно) переходит из одного состояния в
другое;
· с непрерывными состояниями, если происходит плавный переход из состояния в состояние.
Для случайных процессов с дискретными состояниями характерны процессы:
1) с дискретным временем, если переходы системы из состояния в состояние происходят в строго
определённые моменты времени t
1
, t
2
, …, t
n
;
2) с непрерывным временем, если переход системы из состояния в состояние возможен в любой
случайный момент времени t.
При анализе случайных процессов с дискретными состояниями удобно пользоваться так
называемым графом состояний. Он изображает возможные состояния системы и её возможные
переходы из состояния в состояние.
Пусть имеется система S с дискретными состояниями S
1
, S
2
, …, S
n
. Каждое состояние
p
1
p
2
p
3
p
4
1
2
3
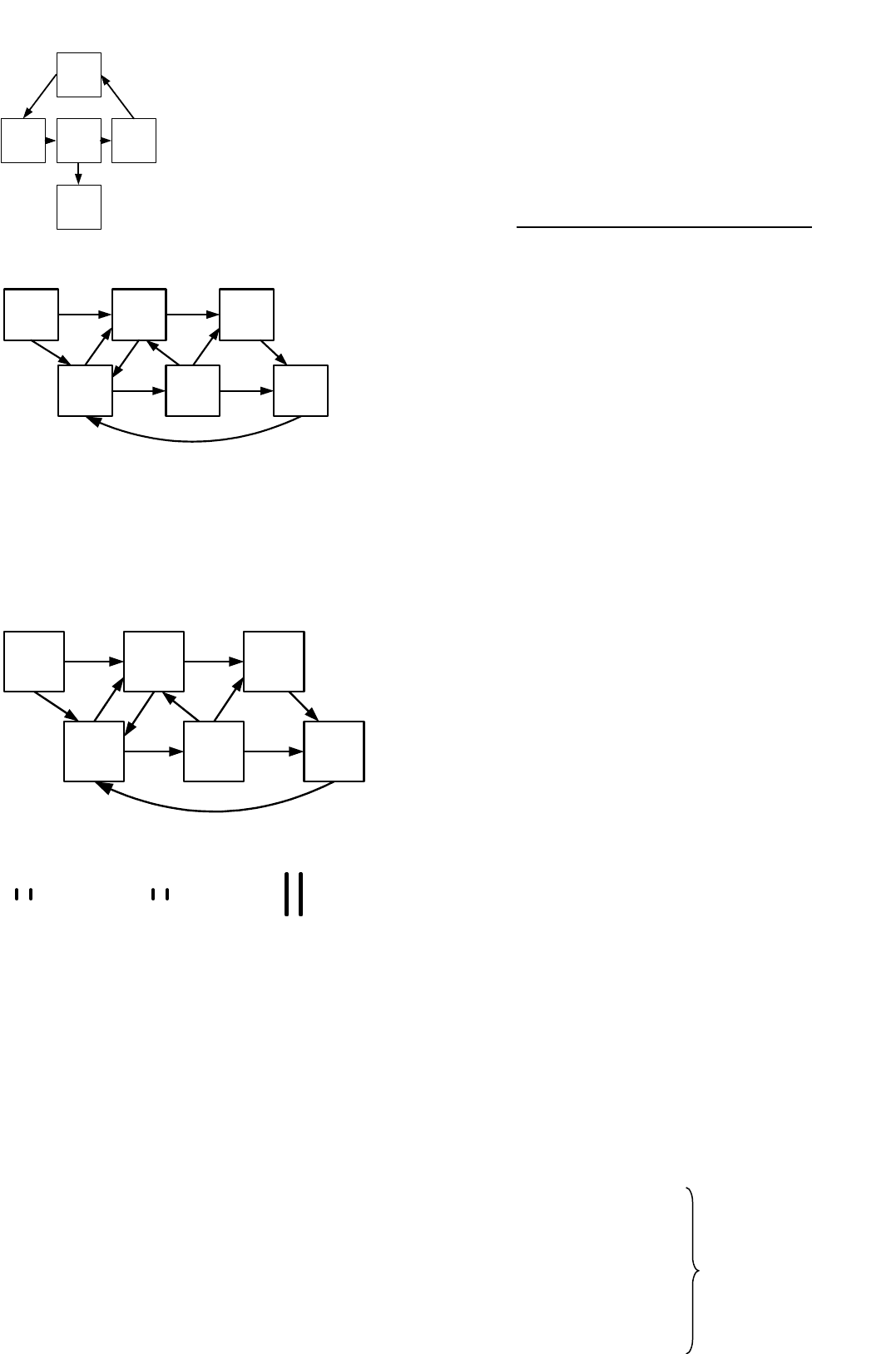
изображается прямоугольником, а возможные переходы из состояния в состояние – стрелками.
Пример.
Станок – система S, которая может находиться в одном из пяти возможных
состояний:
S
1
– исправен, работает;
S
2
– неисправен, ожидает осмотра;
S
3
– осматривается;
S
4
– ремонтируется;
S
5
– списан.
1) Рассмотрим первый случай – процессы с дискретным временем. Система
S оказывается в тех или других состояниях, ведя себя, например, следующим
образом: S
1
S
2
S
4
S
6
… или S
1
S
3
S
2
S
3
S
5
S
6
S
2
…
Условимся обозначать S
i
(k)
событие, состоящее в том, что
после k шагов система находится в состоянии S
i
. Процесс,
происходящий в системе можно представить как цепочку
событий: S
1
(1)
, S
3
(2)
, S
2
(3)
, S
3
(4)
, S
5
(5)
, S
6
(6)
, S
2
(7)
.
Предполагается, что при любом событии k система S
может оказаться в любом состоянии S
i
. Обозначим вероятности
этих событий p
S
(k).
Вероятность событий после первого шага: p
1
(1) = P(S
1
(1)
);
p
2
(1) = P(S
2
(1)
); p
3
(1) = P(S
3
(1)
); …; p
n
(1) = P(S
n
(1)
).
Вероятность событий после второго шага: p
1
(2) = P(S
1
(2)
); p
2
(2) = P(S
2
(2)
); p
3
(2) = P(S
3
(2)
); …; p
n
(2) =
P(S
n
(2)
).
Вероятность событий после k-ого шага: p
1
(k) = P(S
1
(k)
); p
2
(k) = P(S
2
(k)
); p
3
(k) = P(S
3
(k)
); …; p
n
(k) =
P(S
n
(k)
).
Для каждого шага k p
1
(k) + p
2
(k) + p
3
(k) + … + p
n
(k) = 1, так как это – вероятности несовместимых
событий.
При рассмотрении марковских цепей удобно
пользоваться графом состояний, на котором у стрелок
переходов из состояния в состояние проставлены
вероятности таких переходов. Такой граф называется
"размеченный граф состояний".
Допустим, что для каждого состояния известна
вероятность перехода в любое другое состояние за один
шаг. Вероятность перехода из состояния S
i
в состояние S
j
обозначается P
ij
. Вероятности переходов из любого
состояния в любое другое удобно записывать в виде
матрицы (таблицы):
nnnj2n1n
inij2i1i
n2j22221
n1j11211
ij
P...P...PP
.............
P...P...PP
.............
P...P...PP
P...P...PP
P
.
Если вероятность перехода из состояния в состояния равна нулю, значит, такой переход
невозможен. Вероятность P
ii
(P
11
, P
22
и т. д.) обозначает задержку систему в одном и том же состоянии.
Имея в распоряжении размеченный граф состояний (матрицу переходных состояний) можно
найти вероятности состояний системы после любого шага k.
Предположим, что в начальный момент система S находится в каком-то состоянии S
m
. Тогда для
начального момента k = 0 имеем
p
1
(0) = 0; p
2
(0) = 0; …; p
m
(0) = 1; …; p
n
(0) = 0.
Найдём вероятности состояний системы после первого шага k = 0. Система перейдёт из
состояния S
m
в любое из состояний S
1
, S
2
, …, S
m
с вероятностями P
m1
, P
m2
, …, P
mm
, …, P
mn
. Вероятности
состояний после первого шага будут
p
1
(1) = P
m1
; p
2
(1) = P
m2
; …; p
m
(1) = P
mm
; …; p
n
(1) = P
mn
.
Найдём вероятности состояний после второго шага k = 2. Для этого задаются гипотезами, что
система после первого шага была в состоянии S
1
, или S
2
, или S
3
, … Вычисления в дальнейшем
производят по формуле полной вероятности.
p
1
(2) = p
1
(1) P
11
+ p
2
(1) P
21
+ … + p
n
(1) P
n1
;
p
2
(2) = p
1
(1) P
12
+ p
2
(1) P
22
+ … + p
n
(1) P
n2
;
S
1
S
2
S
3
S
4
S
5
S
1
S
4
S
3
S
2
S
5
S
6
S
1
S
4
S
3
S
2
S
5
S
6
P
23
P
32
P
13
P
12
P
35
P
43
P
45
P
24
P
46
P
46
P
62
