Лекции - Моделирование и идентификация объектов управления в НГО

Подождите немного. Документ загружается.

1.6. Установление основного содержания модели. На этом подэтапе

определяется основное содержание модели и выбирается метод построения

модели системы, которые разрабатываются на основе принятых гипотез и

предположений. При этом учитываются следующие особенности: а)

формулировка задачи моделирования системы; б) структура системы S и

алгоритмы ее поведения, воздействия внешней среды E; в) возможные

методы и средства решения задачи моделирования.

1.7. Обоснование критериев оценки эффективности системы. Для

оценки качества процесса функционирования моделируемой системы S

необходимо выбрать некоторую совокупность критериев оценки

эффективности, т.е. в математической постановке задача сводится к

получению соотношения для оценки эффективности как функции параметров

и переменных системы. Эта функция представляет собой поверхность

отклика в исследуемой области изменения параметров и переменных и

позволяет определить реакцию системы. Эффективность системы S можно

оценить с помощью интегральных или частных критериев, выбор которых

зависит от рассматриваемой задачи.

1.8. Определение процедур аппроксимации. Для аппроксимации

реальных процессов, протекающих в системе S, обычно используются три

вида процедур: а) детерминированную; б) вероятностную; в) определения

средних значений.

При детерминированной процедуре результаты моделирования

однозначно определяются по данной совокупности входных воздействий,

параметров и переменных системы S. В этом случае отсутствуют случайные

элементы, влияющие на результаты моделирования. Вероятностная

(рандомизированная) процедура применяется в том случае, когда случайные

элементы, включая воздействия внешней среды E, влияют на характеристики

процесса функционирования системы S и когда необходимо получить

информацию о законах распределения выходных переменных. Процедура

определения средних значений используется тогда, когда при моделировании

системы интерес представляют средние значения выходных переменных при

наличии случайных элементов.

1.9. Описание концептуальной модели системы. На этом подэтапе

построения модели системы: а) описывается концептуальная модель M

абстрактных терминах и понятиях; б) дается описание модели с

использованием типовых математических схем; в)принимаются окончательно

гипотезы и предположения; г) обосновывается выбор процедуры

аппроксимации реавльных процессов при построении модели. Таким

образом, на этом подэтапе проводится пробный анализ задачи,

рассматриваются возможные методы ее решения и дается детальное

описание концептуальной модели M

, которая затем используется на втором

этапе моделирования.

1.10. Проверка достоверности концептуальной модели. После того как

концептуальная модель M

описана, необходимо проверить достоверность

некоторых концепций модели перед тем, как перейти к следующему этапу

моделирования системы S. Проверять достоверность концептуальной модели

достаточно сложно, так как процесс ее построения является эвристическим и

такая модель описывается в абстрактных терминах и понятиях. Один из

методов проверки модели M

-применение операций обратного перехода,

позволяющий проанализировать модель, вернуться к принятым

аппроксимациям и, наконец, рассмотреть снова реальные процессы,

протекающие в моделируемой системе S. Проверка достоверности

концептуальной модели M

должна включать: а) проверку замысла модели;

б0 оценку достоверности исходной информации; в) рассмотрение постановки

задачи моделирования; г) анализ принятых аппроксимаций; д) исследование

гипотез и предположений.

Только после тщательной проверки концептуальной модели M

не

позволяют получить достоверные результаты моделирования.

2. Качественный анализ уровня адекватности моделей

Проверка достоверности модели системы. Эта проверка является первой из

проверок, выполняемых на этапе реализации модели. Так как модель

представляет собой приближенное описание процесса функционирования

реальной системы S, то до тех пор, пока не доказана достоверность модели

, нельзя утверждать, что с ее помощью будут получены результаты,

совпадающие с теми, которые могли бы быть получены при проведении

натурного эксперимента с реальной системой S. Поэтому определение

достоверности модели можно считать наиболее важной проблемой при

моделировании систем. От решения этой проблемы зависит степень доверия

к результатам, полученным методом моделирования. Проверка модели на

рассматриваемом подэтапе должна дать ответ на вопрос, насколько

логическая схема модели системы и используемые математические

соотношения отражают замысел модели, сформированный на первом этапе.

При этом проверяются: а) возможность решения поставленной задачи; б)

точность отражения замысла в логической схеме; в) полнота логической

схемы модели; г) правильность используемых математических соотношений.

Только после того, как разработчик убеждается путем

соответствующей проверки в правильности всех этих положений, можно

считать, что имеется логическая схема модели системы S, пригодная для

дальнейшей работы по реализации модели на ЭВМ.

При реализации моделирующих алгоритмов на ЭВМ вырабатывается

информация о состояниях процесса функционирования исследуемых систем

z (t) є Z. Эта информация является исходным материалом для определения

приближенных оценок искомых характеристик, получаемых в результате

машинного эксперимента, т.е. критериев оценки. Критерием оценки будем

называть любой количественный показатель, по которому можно судить о

результатах моделирования системы. Критериями оценки могут служить

показатели, получаемые на основе процессов, действительно протекающих в

системе или получаемых на основе специально сформированных функций

этих процессов.

В ходе машинного эксперимента изучается поведение исследуемой

модели M процесса функционирования системы S на заданном интервале

времени [О,Т].Поэтому критерий оценки является в общем случае векторной

случайной функцией, заданной на этом же интервале:

).(...,),(),(()(

tqtqtqtq



Часто используют более простые критерии оценки, например,

вероятность определенного состояния системы в заданный момент времени t

* є [О, Т], отсутствие отказов и сбоев в системе на интервале [О,Т] и т.д. При

интерпретации результатов моделирования вычисляются различные

статистические характеристики закона распределения критерия оценки.

Рассмотрим общую схему фиксации и обработки результатов

моделирования системы, которая приведена на рис. 3. Будем рассматривать

гипотетическую модель M, предназначенную для исследования поведения

системы S на интервале времени [О, Т]. В общем случае критерием

интерпретации результатов моделирования является нестационарный

случайный n-мерный процесс

.0),( Tttq 

Полагаем для определенности,

что состояние моделируемой системы S проверяется каждые Δ t временных

единиц, т.е. используется «принцип Δ t». При этом вычисляют значения

kOjtjq ,),( 

, критерия

).(tq

Таким образом, о свойствах случайного

процесса

)(tq

судят по свойствам случайной последовательности

kOjtjq ,),( 

, или, иначе говоря, по свойствам m-мерного вектора вида

 

.),1()),(

,)1(...,),(),0((

tkTknmTq

tkqtqqq





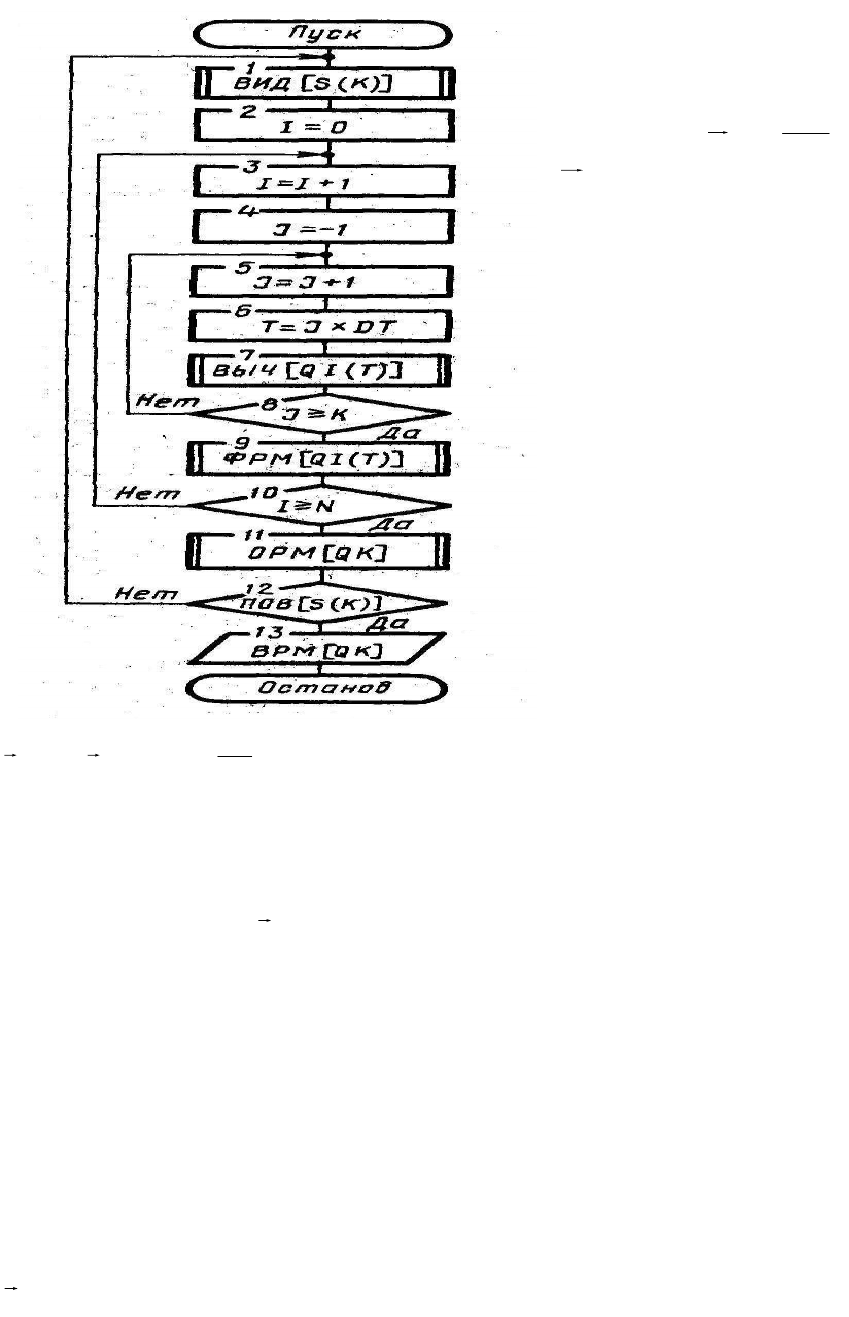
Процесс функционирования

системы S на интервале [О, Т]

моделируется N-кратно с

получением независимых

реализаций

,,1, Niq



вектора

Работа модели на интервале

[О, Т] называется прогоном

модели.

На схеме, изображенной

на рис. 3, обозначено I≡i; J≡j;

K≡k; N≡N; T≡t; DT≡Δt; Q≡q.

В общем случае

алгоритмы фиксации и

статистической

обработки данных

моделирования содержат

три цикла. Полагаем, что

имеется машинная

модель M

системы S.

В н у т р е н и й ц и к л (блоки

5-8), позволяет получить

последо-вательность

kjtjqtq

,0),()( 

в моменты времени t=0, Δ t, 2 Δ t, …, k Δ t=T.

Рис.3.

Основной блок 7 реализует процедуру вычисления

последовательности

 

.)(:)( TIQВЫЧtq

Именно в этом блоке имитируется

процесс функционирования моделируемой системы S на интервале времени

[О, Т].

П р о м е ж у т о ч н ы й ц и к л (блоки 3-10), в котором организуется

N-кратное повторение прогона модели, позволяющее после соответствующей

статистической обработки результатов судить об оценках характеристик

моделируемого варианта системы. Окончательное моделирование варианта

системы S может определяться не только заданным числом реализаций (блок

10), как это показано на схеме, но и заданной точностью результатов

моделирования. В этом цикле содержится блок 9, реализующий процедуру

фиксации результатов моделирования по i-му прогону модели

 

.)(:)( TIQФРМtq

В н е ш н и й ц и к л (блоки 1-12) охватывает оба предшествующих

цикла и дополнительно включает блоки 1, 2, 11, 12, управляющие

последовательностью моделирования вариантов системы S. Здесь

организуется поиск оптимальных структур, алгоритмов и параметров

системы S, т.е. блок 11 обрабатывает результаты моделирования

исследуемого k–го варианта системы OPM [Q, K], блок 12 проверяет

удовлетворительность полученных оценок характеристик процесса

функционирования системы

)(

требуемым (ведет поиск оптимального

варианта системы ПОВ [S (K)], блок 1 изменяет структуру, алгоритмы и

параметры системы S на уровне ввода исходных данных для очередного k–го

варианта системы ВИД [S (K)]. Блок 13 реализует функцию выдачи

результатов моделирования по каждому k–му варианту модели системы S

т.е. ВРМ [Q K].

Рассмотренная схема позволяет вести статистическую обработку

результатов моделирования в наиболее общем случае при нестационарном

критерии

)(tq

. В частных случаях можно ограничиться более простыми

схемами.

Если свойства моделируемой системы S определяются значением

критерия

)(tq

в некоторый заданный момент времени, например в конце

периода функционирования модели t=kΔ t=T, то обработка сводится к оценке

распределения n-мерного вектора

)(tq

по независимым реализациям

Nitq

,1),( 

, полученным в результате N прогонов модели.

Если в моделируемой системе S по истечению некоторого времени с

начала работы t

Δ t установится стационарный режим, то о нем можно

судить по одной, достаточно длинной реализации

)(

критерия

)(tq

стационарного и эргодического на интервале [t

, Т]. Для рассмотренной

схемы это означает, что исключается средний цикл (n=1) и добавляется

оператор, позволяющий начать обработку значений

)(

tjq 

при j≥k

Другая особенность применяемых на практике методов

статистической обработки результатов моделирования связана с

исследованием процесса функционирования систем с помощью моделей

блочной конструкции. В этом случае часто приходится применять раздельное

моделирование отдельных блоков модели, когда имитация входных

воздействий для одного блока проводится на основе оценок критериев,

полученных предварительно на другом блоке модели. При раздельном

моделировании может иметь место либо непосредственная запись в

накопителе реализаций критериев, либо их аппроксимация, полученная на

основе статистической обработки результатов моделирования с

последующим использованием генераторов случайных чисел для имитации

этих воздействий.

Л.1 стр.115-132, Л.2,стр. 54-58

Контрольные вопросы

1. Анализ результатов моделирования системы.

2. Представление результатов моделирования.

3. Интерпретация результатов моделирования.

ЛЕКЦИЯ 8. Постановка задачи идентификации

1. Общая схема идентификации. Основные этапы идентификации.

2. Априорная и апостериорная информация. Классификация методов

идентификации.

Идентификация математического описания объекта является основным

этапом в построении адекватной математической модели процесса и поэтому

представляет собой одну из центральных задач математического

моделирования химико-технологических процессов. Как уже отмечалось,

большинство таких процессов представляет собой многофазную много-

компонентную среду, распределенную в пространстве и во времени. Су-

щественной особенностью этих процессов является их детерминированно-

стохастическая природа, определяемая наложением стохастических особен-

ностей гидродинамической обстановки в аппарате на процессы массо-и

теплопереноса. Как следствие этого, параметры математических моделей

отражают стохастические особенности протекания процесса и определяются

статистическими методами.

В настоящее время наиболее разработана теория оценивания линейных

по параметрам математических моделей. Однако большинство моделей

химико-технологических процессов нелинейны по параметрам, что создает

значительные трудности при решении задач их идентификации. Поэтому

часто идентификацию нелинейных моделей проводят либо с помощью при-

ближенных оценок, либо путем линеаризации исходной модели химико-

технологического процесса. В настоящей главе будут рассмотрены методы

идентификации как линейных, так и нелинейных математических моделей.

Так как наряду с оценкой неизвестных параметров задача идентифи-

кации подразумевает сравнение рассчитываемых по модели переменных

состояния химико-технологического процесса с наблюдаемыми (экспери-

ментальными) значениями, то в данной главе рассматриваются и методы

установления соответствия (адекватности) модели реальному объекту.

Л.1 стр.145-162, Л.2,стр. 74-78

Контрольные вопросы

1. Основные этапы идентификации

2. Априорная и апостериорная информация

3. Классификация методов идентификации

ЛЕКЦИЯ 9. Критерий идентификации

1. Критерий идентификации.

2. Функционал невязки.

Критерии адекватности моделей. Математическая модель объекта

является лишь его определенным в рамках принятых допущений аналогом.

Поэтому значения переменньгх, получаемые на модели и объекте,

различаются. Здесь возникает задача установления близости модели

реальному объекту (установления адекватности модели). Прежде чем

приступить к проверке и установлению адекватности, необходимо

выработать критерий, который позволил бы сделать заключение о

соответствии модели и объекта. Они базируются в основном на методах

дисперсионного анализа и анализа остатков.

Дисперсионный анализ моделей используется для сравнения величин

остятков с величинами характеризуюшими ошибку измерений. Используя

такое сравненне, исследователь способен установить как общую

адекватность модели, так и способы ее дальнейшего упрощения с помощью

выбрасывания из модели незначимых членов. Для этого вычисляют

величины сумм квадратов, характеризующие соответственно разброс

экспериментальных данных и разброс рассчитанных по модели значений

отклика. Разности называемые остатками, представляют собой меру

неспособности модели точно описать экспериментальные данные.

Очевидно, что если испытывая модель истинна, то остатки фактически есть

оценки экспериментальной ошибки измерений.

На основании метода наименьших квадратов можно показать, что для

перечисленных сумм справедливо следующее равенство:

SS (1) = SS (2) + SS (3).

При проведении дисперсионного анализа каждому отдельному изме-

рению отклика приписывается одна степень свободы. Следовательно, при

постановке п опытов для однооткликовой ситуации (ситуации с одной за-

меряемой выходной переменной) общая сумма квадратов SS(1) обладает п

степенями свободы; SS(3) имеет (п - р) и SS(2) имеет р степенеи сво-боды (р

— число параметров в модели , с использованием оценок кото-рых

вычисляется сумма SS (2) ).

При проведении повторных измерений в одинаковых условиях экспе-

римента сумма квадратов, содержит всю необходимую информацию об

ошибках измерений.

Если проведено п повторных опытов при каждом из ц различных

условий проведения эксперимента, то сумма квадратов имеет п- 1 степеней

свободы в одном повторном эксперименте (одна степень свободы

используется для оценки), в то время как сумма квадратов обла-дает п- р-q(п

— 1) степенями свободы: поедеднее число определяется как разность между

числом степеней свободы остаточной суммы квадратов.

Суммы квадратов, обусловленные различными источниками, будучи

поделенными на соответствующие числа степеней свободы, определяют

соответствующие дисперсии. Очевидно, что адекватность модели может

определяться отношением дисперсии адекватности модели к дисперсии

воспроизводимости. Если это отношение велико (по крайней мере

существенно больше единицы), то имеются достаточно веские доводы в

пользу того, что испытываемая модель не отражает результаты

эксперимента,

Если модель правильно отражает свойства объекга, то расхождения

между экслериментальными значениями и соответствующими значениями,

вычислениыми по модели, можно рассматривать как случайные величины.

Тогда установление адекватности можно проводить с помощыо проверки

некоторых статистических гипотез. Под статистическими гипотезами

понимают некоторые предположения относительно распределений

генеральной совокупности случайной величины. Проверка гипотезы

заключается в сопоставлении статистических показателей, критериев

проверки, вычисляемых по выборке, со значениями этих показателей,

определенными в предположении, что проверяемая гипотеза верна. Чтобы

принять или отвергнуть гипотезу, задают уровень значимости р (обычно от

0,1 до 5 %), который определяет вероятность того, что верная гипотеза будет

отвергнута на основании анализа выборки.

Оценка адекватности однооткликовых моделей с помощью критерия

Фишера. В случае однооткликовых моделей адекватность может быть

проверена с помощью критерия Фишера (Ғ -критерия).

Основная гипотеза, которая при этом проверяется, состоит в следую-

щем : можно ли считать сравниваемые выборочные дисперсии оценками

одной и той же генеральной дисперсии ? Если да, то дисперсии незначимо

отличаются друг от друга. Рассчитанные по модели значения удовлет-

ворительно совпадают с экспериментальными и модель адекватна объек-ту

в пределах точности эксперимента. В противном случае модель неадекватна

обьекту.

Л.1 стр.166-174, Л.2,стр. 81-88

Контрольные вопросы

1. Критерий идентификации

2. Функционал невязки

3. Минимизация функционала невязки

ЛЕКЦИЯ 10. Общие задачи статистической идентификации.

1. Структурная статистическая идентификация.

2. Организация статистической процедуры идентификации модели..

В практике моделирования систем информатики наиболее часто

приходится иметь дело с объектами, которые в процессе своего

функционирования содержат элементы стохастичности или подвергаются

стохастическим воздействиям внешней среды. Поэтому основным методом

получения результатов с помощью имитационных моделей таких

стохастических систем является метод статистического моделирования на

ЭВМ, использующий в качестве теоретической базы предельные теоремы

теории вероятностей. Возможность получения пользователем модели

результатов статистического моделирования сложных систем в условиях

ограниченности машинных ресурсов существенно зависит от эффективности

процедур генерации псевдослучайных последовательностей на ЭВМ,

положенных в основу имитации воздействий на элементы моделируемой

системы.

Общая характеристика метода статистического моделирования

На этапе исследования и проектирования систем при построении и

реализации машинных моделей (аналитических и имитационных) широко

используется метод статистических испытаний (Монте-Карло), который

базируется на использовании случайных чисел, т. е. возможных значений

некоторой случайной величины с заданным распределением вероятностей.

Статистическое моделирование представляет собой метод получения с

помощью ЭВМ статистических данных о процессах, происходящих в

моделируемой системе. Для получения представляющих интерес оценок

характеристик моделируемой системы S с учетом воздействий внешней сре-

ды Е статистические данные обрабатываются и классифицируются с

использованием методов математической статистики [10, 13, 18].

Сущность метода статистического моделирования. Таким образом,

сущность метода статистического моделирования сводится к построению для

процесса функционирования исследуемой системы S некоторого

моделирующего алгоритма, имитирующего поведение и взаимодействие

элементов системы с учетом случайных входных воздействий и воздействий

внешней среды Е, и реализации этого алгоритма с использованием

программно-технических средств ЭВМ.

Различают две области применения метода статистического мо-

делирования: 1) для изучения стохастических систем; 2) для решения

детерминированных задач. Основной идеей, которая используется для

rrрешения детерминированных задач методом статистического

моделирования, является замена детерминированной задачи эквивалентной

схемой некоторой стохастической системы, выходные характеристики

последней совпадают с результатом решения детерминированной задачи.

Естественно, что при такой замене вместо точного решения задачи

получается приближенное решение и погрешность уменьшается с

увеличением числа испытаний (реализации моделирующего алгоритма) N.

В результате статистического моделирования системы S получается серия

частных значений искомых величин или функций, статистическая обработка

которых позволяет получить сведения о поведении реального объекта или

процесса в произвольные моменты времени. Если количество реализации N

достаточно велико, то полученные результаты моделирования системы

приобретают статистическую устойчивость и с достаточной точностью могут

быть приняты в качестве оценок искомых характеристик процесса функ-

ционирования системы S.

Теоретической основой метода статистического моделирования систем на

ЭВМ являются предельные теоремы теории вероятностей. Множества

случайных явлений (событий, величин) подчиняются определенным

закономерностям, позволяющим не только прогнозировать их поведение, но

и количественно оценить некоторые средние их характеристики,

проявляющие определенную устойчивость. Характерные закономерности

наблюдаются также в распределениях случайных величин, которые

образуются при сложении множества воздействий. Выражением этих зако-

номерностей и устойчивости средних показателей являются так называемые

предельные теоремы теории вероятностей, часть из которых приводится

ниже в пригодной для практического использования при статистическом

моделировании формулировке. Принципиальное значение предельных

теорем состоит в том, что они гарантируют высокое качество статистических

оценок при весьма большом числе испытаний (реализации) N. Практически

приемлемые при статистическом моделировании количественные оценки

характеристик систем часто могут быть получены уже при сравнительно

небольших (при использовании ЭВМ) N.

Неравенство Чебышева. Для неотрицательной функции g () случайной

величины  и любого K>0 выполняется неравенство

P{g()>=K}M[g()]/K. (4.1)

В частности, если g()=(—x)

и К=k



(где х—среднее арифметическое;