Лекции - Модели и методы АПР

Подождите немного. Документ загружается.

Введение..................................................................................................................................................1

Постановка задачи анализа объектов с распределенными параметрами........................................15

Метод конечных разностей..................................................................................................................19

Метод конечных элементов.................................................................................................................23

Метод граничных элементов...............................................................................................................33

Постановка задачи анализа объектов с сосредоточенными параметрами......................................36

Эквивалентные схемы технических объектов...............................................................................42

Рекомендации к составлению эквивалентных схем......................................................................47

Элементы теории графов......................................................................................................................51

Метод получения топологических уравнений на основе матрицы контуров и сечений...............52

Узловой метод получения математических моделей систем.......................................................57

Метод переменных состояния.........................................................................................................61

Математические модели технических объектов для получения частотных характеристик.........63

Методы анализа повышенной эффективности..................................................................................65

Введение

Проектирование технического объекта связано с созданием,

преобразованиями и представлением в принятой форме образа этого объекта.

Образ объекта или его составных частей может создаваться в воображении

человека в результате творческого процесса или генерироваться по некоторым

алгоритмам в процессе взаимодействия человека и ЭВМ. В любом случае

проектирование начинается при наличии задания на проектирование, которое

отражает потребности общества в получении некоторого технического изделия.

Это задание представляется в виде тех или иных документов и является исходным

(первичным) описанием объекта. Результатом проектирования, как правило,

служит полный комплект документации, содержащий достаточные сведения для

изготовления объекта в заданных условиях. Эта документация представляет собой

окончательное описание объекта.

Проектирование - процесс, заключающийся в преобразовании исходного

описания объекта в окончательное описание на основе выполнения комплекса

работ исследовательского, расчетного и конструкторского характера.

Преобразование исходного описания в окончательное порождает

промежуточные описания, которые являются предметом рассмотрения с целью

определения окончания проектирования или выбора путей его продолжения.

Такие описания называют проектными решениями.

Проектирование, при котором все или часть проектных решений получают

путем взаимодействия человека и ЭВМ, называют автоматизированным, а

проектирование, при котором ЭВМ не используется, - неавтоматизированным.

Проектирование как процесс, развивающийся во времени, расчленяется на

стадии, этапы, проектные процедуры и операции.

При проектировании сложных систем выделяют стадии предпроектных

исследований, технического задания и технического предложения, эскизного,

технического, рабочего проектов, испытаний и внедрения.

На стадиях предпроектных исследований, технического задания и

технического предложения на основании изучения потребностей общества в

получении новых изделий, научно-технических достижений в данной и смежной

отраслях промышленности, имеющихся ресурсов определяют назначение,

основные принципы построения технического объекта и формулируют

техническое задание (ТЗ) на его проектирование. Эти стадии называют также

стадиями научно-исследовательских работ (НИР).

На стадии эскизного проекта (иначе стадии опытно-конструкторских

работ - ОКР) проверяется корректность и реализуемость основных принципов и

положений, определяющих функционирование будущего объекта, и создается его

эскизный проект.

На стадии технического проекта выполняется всесторонняя проработка

всех частей проекта, конкретизируются и детализируются технические решения.

На стадии рабочего проекта формируется вся необходимая документация

для изготовления изделия. Далее создается и испытывается опытный образец или

пробная партия изделий, по результатам испытаний вносятся необходимые

коррективы в проектную документацию, после чего осуществляется внедрение в

производство на выбранном предприятии.

Этап проектирования - часть процесса проектирования, включающая в себя

формирование всех требующихся описаний объекта, относящихся к одному или

нескольким иерархическим уровням и аспектам. Часто названия этапов совпадают

с названиями соответствующих иерархических уровней и аспектов. Так,

проектирование технологических процессов расчленяют на этапы разработки

принципиальных схем технологического процесса, маршрутной технологии,

операционной технологии и получения управляющей информации на машинных

носителях для программно-управляемого технологического оборудования.

Составные части этапа проектирования называют проектными процедурами.

Проектная процедура - часть этапа, выполнение которой заканчивается

получением проектного решения. Каждой проектной процедуре соответствует

некоторая задача проектирования, решаемая в рамках данной процедуры. Более

мелкие составные части процесса проектирования, входящие в состав проектных

процедур, называют проектными операциями. Примерами проектных процедур

могут служить: оформление чертежа изделия, расчет параметров усилителя,

выбор типовой конструкции для построения электродвигателя, а примерами

проектных операций - вычерчивание типового графического изображения

(зубчатого зацепления, рамки чертежа и т. п.), решение системы алгебраических

уравнений, описывающих статическое состояние усилителя, расчет показателей

эффективности очередного варианта построения электродвигателя.

Понятия уровня и аспекта относятся к структурированию представлений о

проектируемом объекте, а понятие этапа - к структурированию процесса

проектирования.

Окончательное описание проектируемого объекта представляет собой

полный комплект схемной, конструкторской и технологической документации,

предназначенной для использования в процессе изготовления и эксплуатации

этого объекта. Важное значение в этих описаниях имеют математические модели

объектов проектирования, так как выполнение проектных процедур при

автоматизированном проектировании основано на оперировании

математическими моделями. При проектировании используют математические

модели, отражающие свойства объекта, существенные с позиции инженера.

Современный инженер обязан представлять особую роль математических

моделей и анализа проектных решений при проектировании технических

объектов. Создание и сопровождение программно-методических комплексов

проектирования невозможно без четкого осмысления методов и алгоритмов

реализуемых в них.

Математическое обеспечение автоматизированного проектирования

включает в себя математические модели объектов проектирования, методы и

алгоритмы выполнения проектных процедур.

Классификация ММ и способы получения

В автоматизированных проектных процедурах вместо еще не

существующего проектируемого объекта оперируют некоторым квазиобъектом -

моделью, которая отражает некоторые интересующие исследователя свойства

объекта. Модель может быть физическим объектом (макет, стенд) или

спецификацией. Среди моделей-спецификаций различают функциональные,

поведенческие, информационные в виде диаграмм сущность - отношение,

структурные модели (описания). Эти модели называют математическими, если

они формализованы средствами аппарата и языка математики. Математические

модели могут быть геометрическими, топологическими, динамическими,

логическими и т. п., если они отражают соответствующие свойства объектов.

Наряду с математическими моделями при проектировании используют

функциональные EDEF0-модели, геометрические модели-чертежи.

Математическая модель (ММ) - совокупность математических объектов

(чисел, символов, множеств и т. д.) и связей между ними, отражающих

важнейшие для проектировщика свойства проектируемого технического объекта.

Математические модели (ММ) служат для описания свойств объектов в

процедурах автоматизированного проектирования. Если проектная процедура

включает создание ММ и оперирование ею с целью получения полезной

информации об объекте, то говорят, что процедура выполняется на основе

математического моделирования.

Классификация математических моделей.

Основные признаки классификации и типы ММ, применяемые в САПР, даны

в таблице 1.

Таблица 1.

Признак классификации Математические модели

Характер отображаемых свойств

объекта

Структурные; функциональные

Принадлежность к иерархическому

уровню

Микроуровня; макроуровня;

метауровня

Степень детализации описания

внутри одного уровня

Полные; макромодели

Способ представления свойств

объекта

Аналитические, алгоритмические,

имитационные

Способ получения модели Теоретические, эмпирические

По характеру отображаемых свойств объекта ММ делятся на

структурные и функциональные.

Структурные ММ предназначены для отображения структурных свойств

объекта. Различают структурные ММ топологические и геометрические.

В топологических ММ отображаются состав и взаимосвязи элементов

объекта. Топологические модели могут иметь форму графов, таблиц (матриц),

списков и т. п.

В геометрических ММ отображаются геометрические свойства объектов, в

них дополнительно к сведениям о взаимном расположении элементов содержатся

сведения о форме деталей. Геометрические ММ могут выражаться совокупностью

уравнений линий и поверхностей; алгебрологических соотношений,

описывающих области, составляющие тело объекта; графами и списками,

отображающими конструкции из типовых конструктивных элементов и т. п.

Функциональные ММ предназначены для отображения физических или

информационных процессов, протекающих в объекте при его функционировании

или изготовлении. Функциональные ММ представляют собой системы уравнений,

связывающих фазовые переменные, внутренние, внешние и выходные параметры,

т.е. алгоритм вычисления вектора выходных параметров Y при заданных

векторах параметров элементов X и внешних параметров Q.

Количество иерархических уровней при моделировании определяется

сложностью проектируемых объектов и возможностью средств проектирования.

Однако для большинства предметных областей можно отнести имеющиеся

иерархические уровни к одному из трех обобщенных уровней, называемых далее

микро-, макро- и метауровнями.

В зависимости от места в иерархии описаний математические модели

делятся на ММ, относящиеся к микро-, макро- и метауровням.

Особенностью ММ на микроуровне является отражение физических

процессов, протекающих в непрерывных пространстве и времени. Типичные ММ

на микроуровне - дифференциальные уравнения в частных производных (ДУЧП).

На макроуровне используют укрупненную дискретизацию пространства по

функциональному признаку, что приводит к представлению ММ на этом уровне в

виде систем обыкновенных дифференциальных уравнений (ОДУ). Системы ОДУ

являются универсальными моделями на макроуровне, пригодными для анализа

как динамических, так и установившихся состояний объектов. Модели для

установившихся режимов можно также представить и виде систем

алгебраических уравнений. Порядок системы уравнений зависит от числа

выделенных элементов объекта. Если порядок системы приближается к 10

, то

оперирование моделью становится затруднительным и поэтому необходимо

переходить к представлениям на метауровне.

На метауровне в качестве элементов принимают достаточно сложные

совокупности деталей. Метауровень характеризуется большим разнообразием

типов используемых ММ. Для многих объектов ММ на метауровне по-прежнему

представляются системами ОДУ. Однако так как в моделях не описываются

внутренние для элементов фазовые переменные, а фигурируют только фазовые

переменные, относящиеся к взаимным связям, элементов, то укрупнение

элементов на метауровне означает получение ММ приемлемой размерности для

существенно более сложных объектов, чем на макроуровне.

В ряде предметных областей удается использовать специфические

особенности функционирования объектов для упрощения ММ. Примером

являются электронные устройства цифровой автоматики, в которых возможно

применять дискретное представление таких фазовых переменных, как

напряжения и токи. В результате ММ становится системой логических уравнений,

описывающих процессы преобразования сигналов. Такие логические модели

существенно более экономичны, чем модели электрические, описывающие

изменения напряжений и сил токов как непрерывных функций времени. Важный

класс ММ на метауровне составляют модели массового обслуживания,

применяемые для описания процессов функционирования информационных и

вычислительных систем, производственных участков, линий и цехов.

Структурные модели также делятся на модели различных иерархических

уровней. При этом на низших иерархических уровнях преобладает использование

геометрических моделей, на высших иерархических уровнях используются

топологические модели.

По степени детализации описания в пределах каждого иерархического

уровня выделяют полные ММ и макромодели.

Полная ММ - модель, в которой фигурируют фазовые переменные,

характеризующие состояния всех имеющихся межэлементных связей (т. е.

состояния всех элементов проектируемого объекта), описывающая не только

процессы на внешних выводах моделируемого объекта, но и внутренние

процессы объекта.

Макромодель - ММ, в которой отображаются состояния значительно

меньшего числа межэлементных связей, что соответствует описанию объекта при

укрупненном выделении элементов.

Примечание. Понятия «полная ММ» и «макромодель» относительны и обычно

используются для различения двух моделей, отображающих различную степень детальности

описания свойств объекта.

По способу представления свойств объекта функциональные ММ делятся

на аналитические и алгоритмические.

Аналитические ММ представляют собой явные выражения выходных

параметров как функций входных и внутренних параметров. Такие ММ

характеризуются высокой экономичностью, но получение явного выражения

удается лишь в отдельных частных случаях, как правило, при принятии

существенных допущений и ограничений, снижающих точность и сужающих

область адекватности модели.

Алгоритмические ММ выражают связи выходных параметров с параметрами

внутренними и внешними в форме алгоритма.

Имитационная ММ - алгоритмическая модель, отражающая поведение

исследуемого объекта во времени при задании внешних воздействий на объект.

Примерами имитационных ММ могут служить модели динамических объектов в

виде систем ОДУ и модели систем массового обслуживания, заданные в

алгоритмической форме.

Обычно в имитационных моделях

фигурируют фазовые переменные. Так, на

макроуровне имитационные модели представляют собой системы алгебро-

дифференциальных уравнений:

 

,0 при 0,,/

VVttVdtdV 

(1)

где V - вектор фазовых переменных; t - время; V

- вектор начальных условий. К

примерам фазовых переменных можно отнести токи и напряжения в

электрических системах, силы и скорости - в механических, давления и расходы -

в гидравлических.

Выходные параметры систем могут быть двух типов. Во-первых, это

параметры-функционалы, т. е. функционалы зависимостей V(t) в случае

использования (1). Примеры таких параметров: амплитуды сигналов,

временные задержки, мощности рассеивания и т. п. Во-вторых, это параметры,

характеризующие способность проектируемого объекта работать при

определенных внешних условиях. Эти выходные параметры являются

граничными значениями диапазонов внешних переменных, в которых

сохраняется работоспособность объекта.

При проектировании технических объектов можно выделить две основные

группы процедур: анализ и синтез. Для синтеза характерно использование

структурных моделей, для анализа - использование функциональных моделей. К

математическому обеспечению анализа относятся математические модели,

численные методы, алгоритмы выполнения проектных процедур. Компоненты

МО определяются базовым математическим аппаратом, специфичным для

каждого из иерархических уровней проектирования.

В САПР анализ выполняется математическим моделированием.

Математическое моделирование - процесс создания модели и

оперирование ею с целью получения сведений о реальном объекте.

Моделирование большинства технических объектов можно выполнять на

микро-, макро и метауровнях, различающихся степенью детализации

рассмотрения процессов в объекте.

Математической моделью технического объекта на микроуровне,

называемого распределенным, является система дифференциальных уравнений в

частных производных (ДУПЧ), описывающая процессы в сплошной среде с

заданными краевыми условиями. Независимыми переменными являются

пространственные координаты и время. К моделям на микроуровне относятся

многие сравнения математической физики. Объектами исследования являются

поля физических величин, что требуется при анализе прочности строительных

сооружений или машиностроительных деталей, исследовании процессов в жидких

средах, моделировании концентраций и потоков частиц в электронных приборах и

т. п. С помощью этих уравнений рассчитываются поля механических напряжений

и деформаций, электрических потенциалов, давлений, температур и т.д.

Возможности применения ММ в виде ДУЧП ограничены отдельными деталями,

попытки анализировать с их помощью процессы в многокомпонентных средах,

сборочных единицах, электронных схемах не могут быть успешными из-за

чрезмерного роста затрат машинного времени и памяти.

Система дифференциальных уравнений, как правило, известна (уравнения

Ламе для механики упругих сред; уравнения Навье-Стокса для гидравлики;

уравнения теплопроводности для термодинамики и т.д.), но точное решение ее

удается получить лишь для частных случаев, поэтому первая задача,

возникающая при моделировании, состоит в построении приближенной

дискретной модели. Для этого используются методы конечных разностей и

интегральных граничных уравнений, одним из вариантов последнего является

метод граничных элементов.

Число совместно исследуемых различных сред (число деталей, слоев

материала, фаз агрегатного состояния) в практически используемых моделях

микроуровня не может быть большим ввиду сложностей вычислительного

характера. Резко снизить вычислительные затраты в многокомпонентных средах

можно, только применив иной подход к моделированию, основанный на

принятии определенных допущений.

Допущение, выражаемое дискретизацией пространства, позволяет перейти к

моделям макроуровня, называемым сосредоточенными. Математической

моделью технического объекта на макроуровне является система алгебраических

и обыкновенных дифференциальных уравнений (ОДУ) с заданными

начальными условиями.

В этих уравнениях независимой переменной является время t, а вектор

зависимых переменных V составляют фазовые переменные, характеризующие

состояние укрупненных элементов дискретизированного пространства. Такими

переменными являются силы и скорости механических систем, напряжения и

силы тока электрических систем, давления и расходы гидравлических и

пневматических систем и т.п.

В основе ММ лежат компонентные уравнения отдельных элементов и

топологические уравнения, вид которых определяется связями между

элементами. Предпосылкой создания единого математического и программного

обеспечения анализа на макроуровне являются аналогии компонентных и

топологических уравнений физически однородных подсистем, из которых состоит

технический объект. Для получения топологических уравнений используются

формальные методы.

Основными методами получения ММ объектов на макроуровне являются:

 Обобщенный метод,

 Табличный метод,

 Узловой метод,

 Метод переменных состояний.

Методы отличаются друг от друга видом и размерностью получаемой

системы уравнений, способом дискретизации компонентных уравнений

реактивных ветвей, допустимыми типами зависимых ветвей. Упрощение описания

отдельных компонентов (деталей) позволяет исследовать модели процессов в

устройствах, приборах, механических узлах, число компонентов в которых может

доходить до нескольких тысяч. Для сложных технических объектов размерность

ММ становится чрезмерно высокой, и для моделирования приходится переходить

на метауровень.

На метауровне моделируют в основном две категории технических объектов:

объекты, являющиеся предметом исследований теории автоматического

управления, и объекты, являющиеся предметом теории массового обслуживания.

Для первой категории объектов возможно использование математического

аппарата макроуровня, для второй категории объектов используют методы

событийного моделирования.

Когда число компонентов в исследуемой системе превышает некоторый

порог, сложность модели системы на макроуровне вновь становится чрезмерной.

Принимая соответствующие допущения, переходят на функционально-логический

уровень, где используется аппарат передаточных функций для исследования

аналоговых (непрерывных) процессов или аппарат математической логики и

конечных автоматов, если объектом исследования является дискретный процесс.

Для исследования еще более сложных объектов (производственные

предприятия и их объединения, вычислительные системы и сети, социальные

системы и др.) применяют аппарат теории массового обслуживания, возможно

использование и некоторых других подходов, например сетей Петри. Эти модели

относятся к системному уровню моделирования.

Требования к математическим моделям и численным методам в САПР.

К математическим моделям предъявляются требования универсальности,

адекватности, точности и экономичности.

Степень универсальности ММ характеризует полноту отображения в модели

свойств реального объекта. Математическая модель отражает лишь некоторые

свойства объекта. Так, большинство ММ, используемых при функциональном

проектировании, предназначено для отображения протекающих в объекте

физических или информационных процессов, при этом не требуется, чтобы ММ

описывала такие свойства объекта, как геометрическая форма составляющих его

элементов. Например, ММ резистора в виде уравнения закона Ома характеризует

свойство резистора пропускать электрический ток, но не отражает габариты

резистора, как детали, его цвет, механическую прочность, стоимость и т. п.

Точность ММ оценивается степенью совпадения значений параметров

реального объекта и значений тех же параметров, рассчитанных с помощью

оцениваемой ММ. Пусть отражаемые в ММ свойства оцениваются вектором

выходных параметров

 

yyyY ,...,,



. Тогда, обозначив истинное и

рассчитанное с помощью ММ значения j-го выходного параметра через

ист

соответственно, определим относительную погрешность



расчета

параметра

как

ист

истм

yy 





(2)

Получена векторная оценка

 



,...,,



. При необходимости сведения

этой оценки к скалярной используют какую-либо норму вектора



, например

 



max





(3)

Адекватность ММ - способность отображать заданные свойства объекта с

погрешностью не выше заданной. Поскольку выходные параметры являются

функциями векторов параметров внешних Q и внутренних X, погрешность



зависит от значений Q и X. Обычно значения внутренних параметров ММ

определяют из условия минимизации погрешности



в некоторой точке Q

ном

пространства внешних переменных, а используют модель с рассчитанным

вектором X при различных значениях Q. При этом, как правило, адекватность

модели имеет место лишь в ограниченной области изменения внешних

переменных - области адекватности (ОА) математической модели:

 





QOA

где

0



- заданная константа, равная предельно допустимой погрешности

модели.

Область адекватности - область в пространстве параметров, в пределах

которой погрешности модели остаются в допустимых пределах. Например,

область адекватности линеаризованной модели поверхности детали определяется

системой неравенств

допij



max

где



доп



- допущенная и предельно допустимая относительные

погрешности моделирования поверхности, максимум берется по всем

координатам и контролируемым точкам;

 

модмодист

ijijijij

xxx 



ист

мод

i-я

координата j-й точки поверхности в объекте и модели соответственно.

В большинстве случаев области адекватности строятся в пространстве

внешних переменных. Так, область адекватности модели электронного

радиоэлемента обычно выражает допустимые для применения модели диапазоны

изменения моделируемых температур, внешних напряжений, частот.

Экономичность ММ характеризуется затратами вычислительных ресурсов

(затратами машинных времени Т

и памяти П

) на ее реализацию. Чем меньше Т

и П

тем модель экономичнее. Вместо значений Т

и П

, зависящих не только от

свойств модели, но и от особенностей применяемой ЭВМ, часто используют

другие величины, например: среднее количество операций, выполняемых при

одном обращении к модели, размерность системы уравнений, количество

используемых в модели внутренних параметров и т. п.

Требования высоких точности, степени универсальности, широкой области

адекватности, с одной стороны, и высокой экономичности, с другой стороны,

противоречивы. Наилучшее компромиссное удовлетворение этих

противоречивых требований зависит от особенностей решаемых задач,

иерархического уровня и аспекта проектирования. Это обстоятельство

обусловливает применение в САПР широкого спектра математических моделей.

Аналогичные требования по точности и экономичности фигурируют при

выборе численных методов решения уравнений модели.

Методика получения математических моделей элементов.

В общем случае процедура получения математических моделей элементов

включает в себя следующие операции:

1. Выбор свойств объекта, которые подлежат отражению в модели. Этот

выбор основан на анализе возможных применений модели и определяет

степень универсальности ММ.

2. Сбор исходной информации о выбранных свойствах объекта. Источниками

сведений могут быть опыт и знания инженера, разрабатывающего модель,

научно-техническая литература, прежде всего справочная, описания

прототипов - имеющихся ММ для элементов, близких по своим свойствам к

исследуемому, результаты экспериментального измерения параметров и т. п.

3. Синтез структуры ММ. Структура ММ - общий вид математических

соотношений модели без конкретизации числовых значений фигурирующих в

них параметров. Структура модели может быть представлена также в

графической форме, например в виде эквивалентной схемы или графа. Синтез

структуры - наиболее ответственная и с наибольшим трудом поддающаяся

формализации операция.

4. Расчет числовых значений параметров ММ. Эта задача ставится как задача

минимизации погрешности модели заданной структуры, т. е.

 

XДX





min

(4)

где X - вектор параметров модели; ХД - область варьирования параметров;



определяется в соответствии с (1) и (2), где

- функция от X, a

ист

определяются по результатам экспериментов либо физических, либо

численных с использованием более точных ММ, если таковые имеются в

иерархическом ряду ММ.

5. Оценка точности и адекватности ММ. Для оценки точности должны

использоваться значения

ист

, которые не фигурировали при решении задачи

(4).

Большую ценность для пользователя представляют не оценки погрешности



, выполненные в одной-двух случайных точках пространства внешних

переменных, а сведения об области адекватности (ОА). Однако определение ОА

требует больших затрат машинного времени. Поэтому расчет ОА выполняется

только при тщательной отработке ММ унифицированных элементов,

предназначенных для многократного применения.

Преобразования математических моделей в процессе получения рабочих

программ анализа.

Реализация функциональных ММ на ЭВМ подразумевает выбор численного

метода решения уравнений и преобразование уравнений в соответствии с

особенностями выбранного метода. Конечная цель преобразований - получение

рабочей программы анализа в виде последовательности элементарных действий

(арифметических и логических операций), реализуемых командами ЭВМ. Все

указанные преобразования исходной ММ в последовательность элементарных

действий ЭВМ выполняет автоматически по специальным программам,

создаваемым инженером-разработчиком САПР. Инженер-пользователь САПР

должен лишь указать, какие программы из имеющихся он хочет использовать.

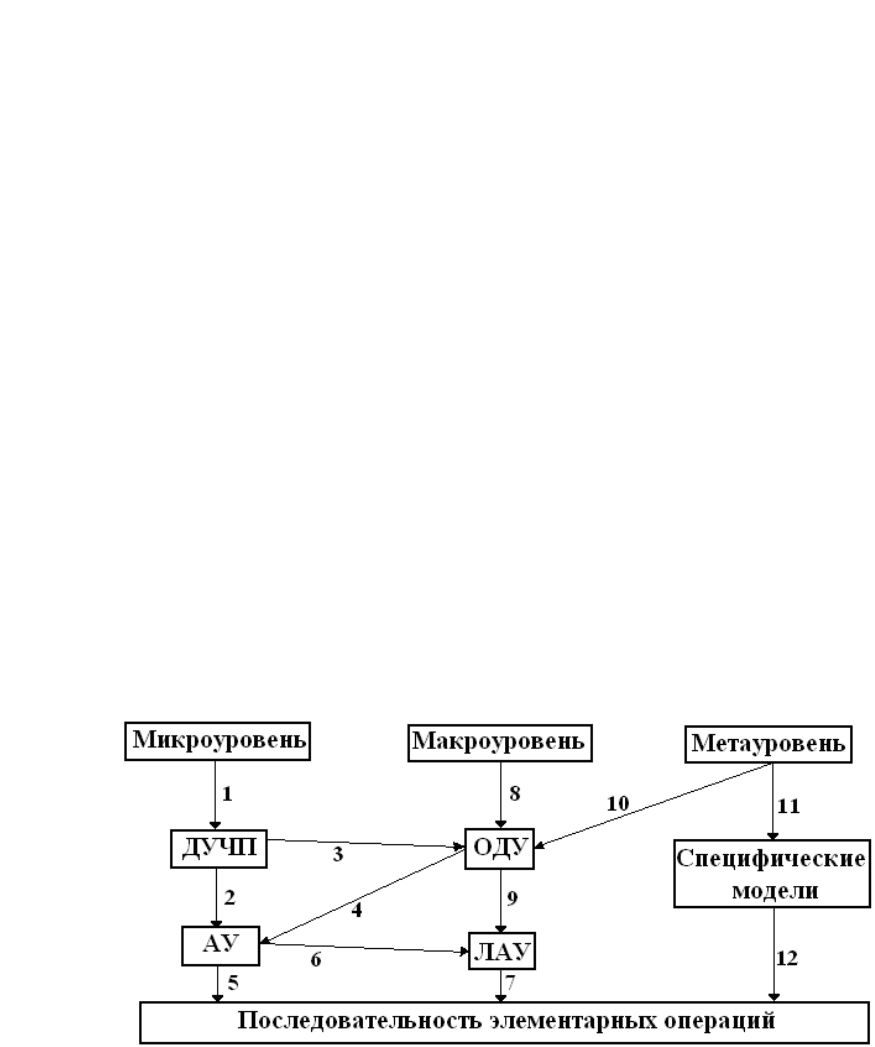
Процесс преобразований ММ, относящихся к различным иерархическим уровням,

иллюстрирует рисунок 1.

Рис. 1.

Инженер-пользователь задает исходную информацию об анализируемом

объекте и о проектных процедурах, подлежащих выполнению, на удобном для

него проблемно-ориентированном входном языке программного комплекса.

Ветви 1 на рис. 2 соответствует постановка задачи, относящейся к микроуровню,

как краевой, чаще всего в виде ДУЧП. Численные методы решения ДУЧП

основаны на дискретизации переменных и алгебраизации задачи. Дискретизация

заключается в замене непрерывных переменных конечным множеством их

значений в заданных для исследования пространственном и временном

интервалах; алгебраизация - в замене производных алгебраическими

соотношениями.

Применяют различные способы дискретизации и алгебраизации переменных

при решении ДУЧП. Эти способы составляют сущность методов числового

решения; большинство используемых методов относится либо к методам

конечных разностей, либо к методам конечных элементов. Если ДУЧП