Лекции - Архитектура систем искусственного интеллекта
Подождите немного. Документ загружается.

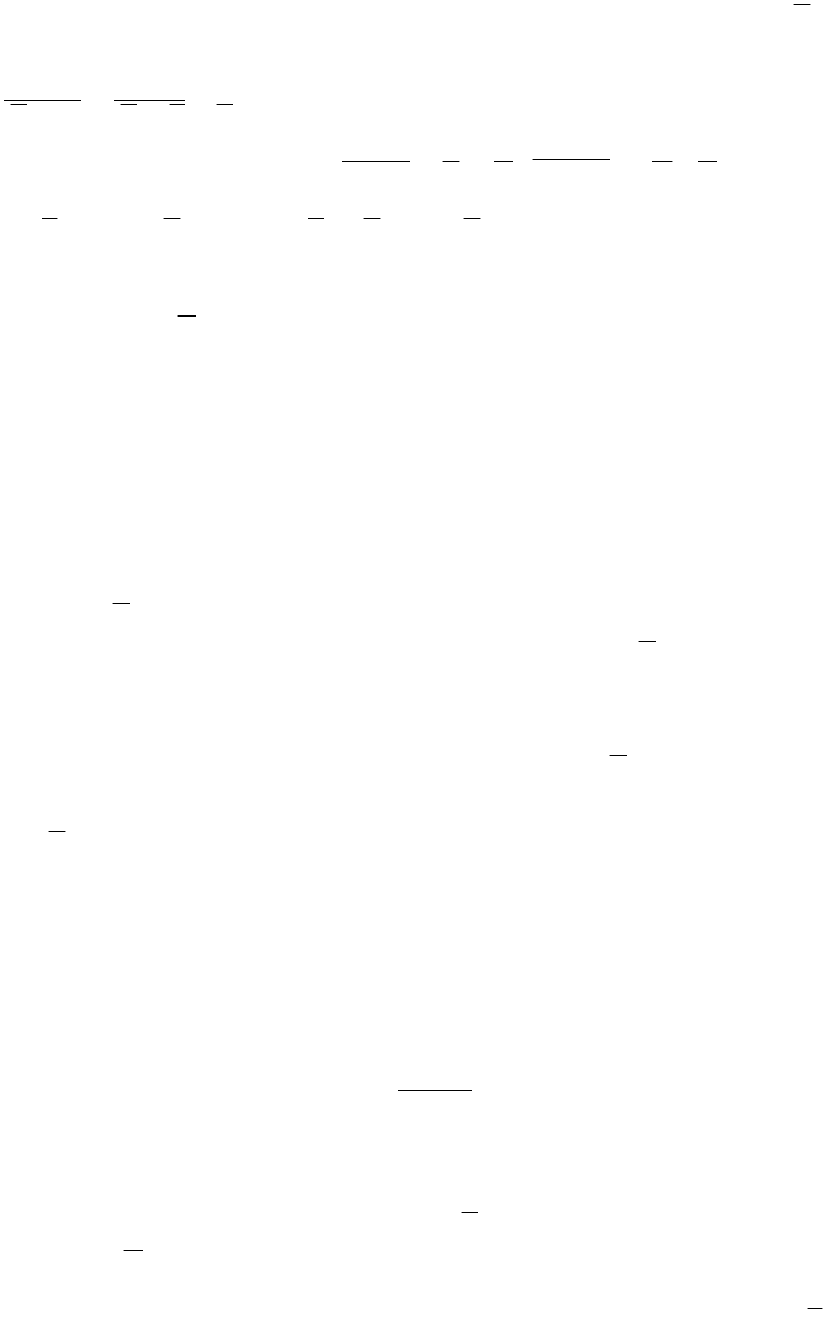
Здесь A, B, C - формулы; х - переменная; t - терм; a, b, c - целые числа; операция (’)
(штрих) соответствует добавлению к числу единицы: а’ = а + 1.
Рассмотрим, например, схему аксиом (7). Заменим формулу А В на
A
В и
подставим (7)
(A B) (A B A)
Далее по правилам де Моргана:
A & B
=
A
B, A B = A& B
получаем:
A& B A& B A A& (B B) A A A = true
Нетрудно видеть, что схема аксиом (7) является тождественно истинной, если
истинна формула A
A
.
Мы, однако, не в состоянии доказать последнюю формулу, т.е. считаем ее истинной
по определению.
Воспользуемся примером, иллюстрирующим это положение.
Рассмотрим высказывание "последовательность 0123456789 встречается в
разложении числа ". Обозначим это высказывание через А. Тогда обратное
высказывание
A
означает, что "последовательность 0123456789 не встречается в
разложении числа ". Для того, чтобы доказать формулу А (или
A
) в принципе нужно
строить бесконечное представление для числа. Поскольку ни один шаг такого "доказа-
тельства", если он не приводит к отысканию требуемой последовательности, не является
законченным, мы не вправе считать, что доказана формула А (
A
). Итак, мы в принципе
не в состоянии укачать финитное (конечное) доказательство ни для формулы А, ни для
формулы
A
.
Будем записывать десятичное разложение числа , а под ним десятичную дробь =
0,333.... При записи каждой очередной цифры в разложении добавляем "3" в . Если
окажется, что высказывание А истинно, то стираем записанное представление для и
полагаем
=
10 - 1
3 10
k
k
где k - число троек, полученных в представлении к данному моменту.
Допустим, что справедлива формула В
B
, где В - это высказывание "число
рационально", и
B
- обратное высказывание, т.е. число не рационально.
Спросим себя, рационально ли или нет? Если не рационально (верно
B
), то

должно быть верно
A
(иначе, если бы была получена последовательность 0123456789),
то
=
10 - 1
3 10
=
x
y
k
k
где х, у - целые, т.е. было бы рационально. Однако, если справедливо
A
, то = 1/3
= 0.333... (бесконечная последовательность). Здесь рационально, что противоречит
предположению о его нерациональности. Итак, не может быть не рациональным. Но
значит рационально. Для этого однако, нужно иметь доказательство А или
A
, чего у
нас нет.
Действительно, если рационально либо мы построили бесконечную
последовательность 0,333... (что невозможно), либо доказали формулу А.
Приведенный пример характеризует так называемое интуиционистское
направление в математике. Так интуиционисты отрицают правило ter‹um non datyr
(третьего не дано). Ими также подвергается критике само понятие отрицания: ложность
любой формулы трактуется ими так, что допущение ведет к противоречию.
Еще один философский пример того же рода демонстрирует так называемый
парадокс лжеца: "если некто говорит, что он лжет, то говорит ли он на самом деле правду
или лжет?"
Обозначим высказывание "Я лгу " через А. Если А истинно, то "некто в
действительности лжет", т.е. должно быть
A
и наоборот. А это означает, что формула A
A
ни истинна, ни ложна (противоречива).
Вернемся, однако, к истине (1.10). Нам осталось определить правила вывода П.
Каждое правило вывода имеет структуру вида:
1 2 n
. . . , , ,
(1.13)
означающую, что если выведены формулы
1
,
2
, ...,
n
, называемые посылками, то
выводима также формула называемая заключением.
Под выводимостью формулы из формул
1
,
2
, ...,
n
, понимается такое отношение
между этими формулами, что всякий раз, когда истинна каждая из формул
1
,
2
, ...,
n
,
истинна также формула .
По определению, аксиома имеет структуру
,

(1.14)
т.е. невыводима из других формул (множество посылок пусто).
Отметим следующие основные свойства для отношения выводимости.
1. Рефлективность:
(1.15)
2. Транзитивность:
,
(1.16)
(если выводима из и из выводима , то из выводима формула ).
3. Монотонность:
,
(1.17)
(если из выводима формула , то присоединение к формулы не отменяет
выводимость ). Отметим, что свойство монотонности в общем случае не имеет места в
некоторых неклассических логиках, рассматриваемых в главе 3.
4. Теорема дедукции:
Если из и выводима формула , то из выводима формула ( -
импликация).
,
(1.18)
Верна также обратная теорема:
,
(1.19)
Теорема дедукции имеет весьма важное значение в логике. Действительно, чтобы
доказать выводимость

(1.20)
заменим формулу эквивалентной формулой , где - символ пустой формулы
(лжи). Используя эквивалентную замену
, получим
,
. (1.21)
Таким образом установлен следующий важный факт: «для доказательства
выводимости
следует показать, что
,
, т.е., что из и
следует противоречие».
В качестве основных правил вывода в логике предикатов используются правила
modus ponens и generaliza{on.
Правило modus ponens:
A, A B
B
(1.22)
утверждает, что если истинны формулы А и А В, то истинна формула B.
Правило generaliza‹on:
C A(x)
C xA(x)
. (1.23)
Справедлива и обратное
C xA(x)
C A(x)
(1.24)
при условии, что С не содержит переменной. х. Это последнее правило существенно
важно при реализации наиболее широко применяемого резолютивного вывода, с
содержанием которого мы познакомимся позднее.
В частности, если С пустая формула, то имеет место
A(x)
xA(x)
(1.25)
Пример правила generaliza‹on:
(x + 5) = x + 10x + 25
x((x + 5) = x = 10x + 25)
2 2
2 2
.

Отметим, что правила вывода в логике предикатов не исчерпывают множества всех
известных правил вывода. Однако, правила вывода имеют иное семантическое
содержание. Об этом следующий параграф.
1.2.2 Примеры стратегии вывода
Рассмотрим формализм нормальных алгоритмов Маркова, в котором правила
вывода реализуются на основе операторов подстановки.
Пусть а и b - произвольные слова. Будем говорить, что слово а входит в слово b, если
существуют такие слова с и d, что b = cad.
Основным правилом вывода является подстановка. Оператор подстановки а Ь
используется для замены левого вхождения слова а на слово b. Для того, чтобы
применить оператор а b к слову e, необходимо, чтобы е содержало а. В последнем
случае будем говорить, что выполнены условия применимости оператора а b. Из
множества операторов, для которых выполнены условия применимости, всегда
выбирается один оператор (например, первый по порядку). Отметим, что вывод считается
детерминированным, если всякий раз условия применимости выполняются не более чем
для одного правила вывода. Алгоритм завершает работу, если либо нет выполнимых
операторов, либо выполняется специальный оператор конца (стоп-оператор).
Пример.
(1) a bc
(2) c ebcc
(3) c d
(4) d
(5) b
(6) есс d.
e - символ пробела.
Рассмотрим, как преобразуется в этой системе слово cad:
cad ebccad eccad dad ad bcd cd ebccd eccd dd d
Здесь внизу под стрелкой указан номер оператора.
(2) (6) (4) (1) (5) (2) (5) (4)(4)(6)(5)

В системах нормальных алгоритмов Маркова выводимость трактуется в
конструктивном смысле - как получение из исходного слова (образца) других слов. Это -
так называемый вывод по образцу (нашедший применение, например, в системах,
использующих фреймы и семантические сети). Каноническая продукционная система
Поста также является системой вывода по образцу.
Пусть x
1
, x
2
, ..., x
n
- попарно различные переменные, которые имеют области
определения D
1
, D
2
, ..., D
m
соответственно. Если переменная х связана некоторым
значением
d
j
1
из D
j
, , то будем вместо х, писать
d
j
1
.
Образец это конструкция
=
x x . . . , x
y y , . . . , y
1 2 m
1 2 m
, ,
,
,
где каждому x
i
, сопоставлен терм у
i
, являющийся либо самой переменной х
i
, (если
она не связана), либо
d
j
1
, если x
i
=
d
j
1
.
Например,
1
=
x x x
x a b
, a D b D
1 2 3
1
2 3
, .
Пусть даны два образца
1
и
2
. Будем говорить, что из
1
и
2
выводится образец
3
, и
писать это:
1 2
3
,
, если выполнены следующие условия:
1)
1
и
2
содержат общие переменные
2) пусть x
i
- одна (любая) из общих переменных, тогда x
i
и в
1
, и в
2
либо связана
одним и тем же значением, либо как минимум одна из них не связана вовсе.
3)
3
образуется путем включения (без дублирования) всех переменных из
1
и
2
.
При этом если общая переменная x
i
связана, скажем в
1
, значением х
i
= а, а в
2
свободна ( не связана), то в
3
x
i
будет иметь значение а. В этом случае говорят,
что переменные в
3
наследуют значения соответствующих переменных в
1
,
2
.
Пример вывода по образцам
1
,
2
образца
3
.
1
=
x x x x
x x a c
1 2 3 4
1 2
,
2
=
x x x
2 x c
1 2 6
2
,
из
1
,
2
выводим образец
3

3
=
x x x x x
2 x a c c
1 2 3 4 6
2
,
Другой важной стратегией, используемой в машинах вывода, является Байесовская
стратегия вывода, которая используется в системах, где детерминированность выводов
является скорее исключением, чем правилом.
Байесовская стратегия вывода оперирует вероятностными знаниями. Ее основная
идея заключается в оценке апостериорной вероятности гипотезы при наличии фактов,
подтверждающих или опровергающих гипотезу. Пусть
Р(Н) = - априорная вероятность гипотезы Н при отсутствии каких- либо свидетельств;
Р(Н:Е) = - апостериорная вероятность гипотезы Н при наличии свидетельства Е.
Согласно теоремы Байеса:
P(H:E) =
P(H& E)
P(E)
,
(1.26)
и
P(H*) = P(E) P(H: E) + P(E) P(H: E),
где Р(Н*) оценивает новую вероятность гипотезы Н с учетом свидетельства Е.
Введем отношение правдоподобия ОП(Н:Е),
OП(H:E) =
P(E:H)
P(E: H)
,
(1.27)
а также формулу для вычисления шансов O(H),
O(H) =
P(H)
1- P(H)
=
P(H)
P(H)
,
(1.28)
Из (1.28) нетрудно обратным преобразованием получить
P(H) =
O(H)
1 + O(H)
,
(1.29)
Теперь формула Байеса (1.8) на языке шансов принимает следующий вид:
O(H*) = O(H) OП(H:E), (1.30)
где O(Н*) - новая оценка шансов для гипотезы Н с учетом свидетельства Е.
Формула (1.30) при наличии многих свидетельств E
1
, E
2
, ..., E
n
принимает вид:
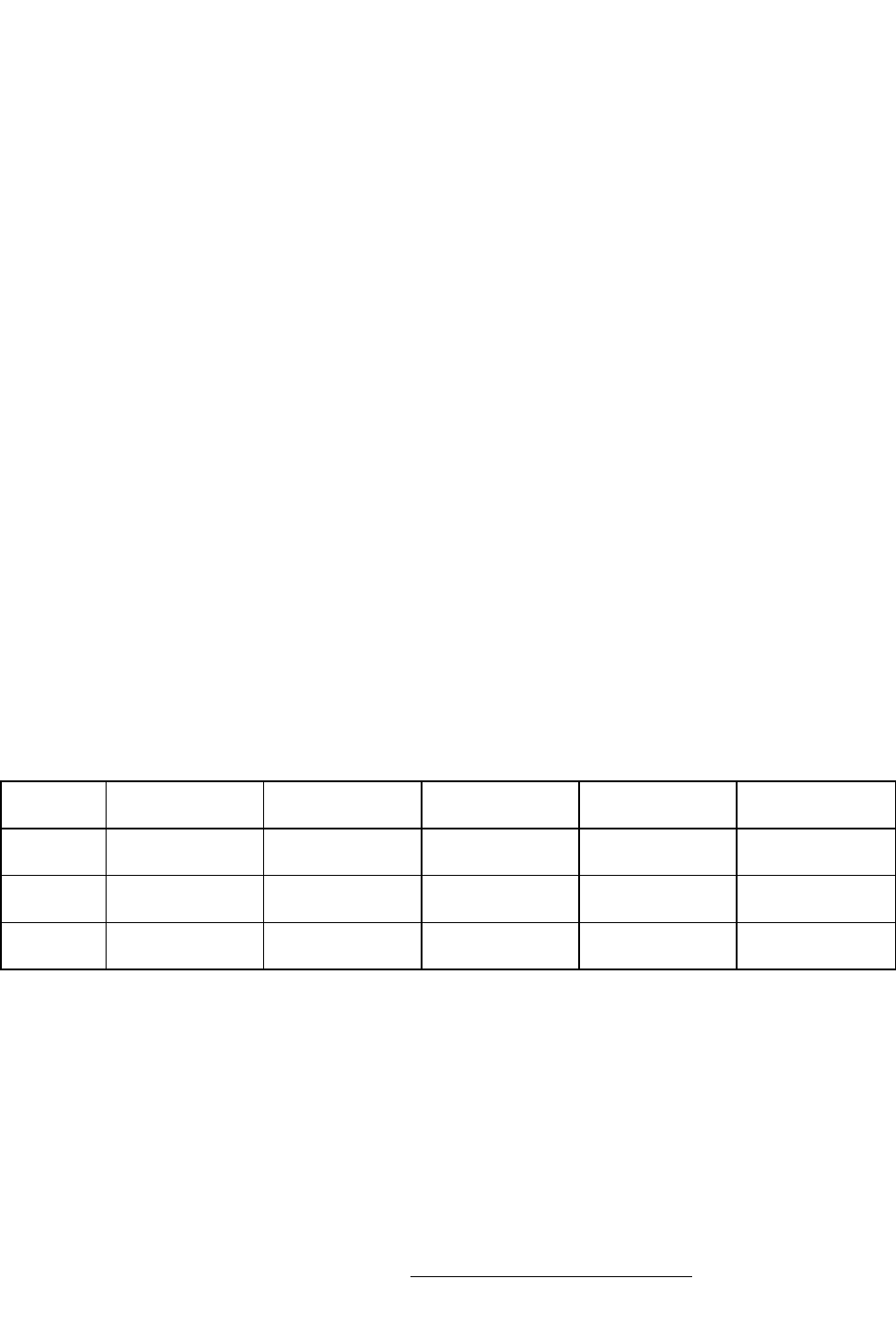
O(H*) = O(H) OП(H:E)
i=1
n
,
(1.31)
Таким образом, на основании формул (1.30) и (1.31) имеется возможность просто
пересчитывать апостериорные вероятности гипотез на основании получаемых
свидетельств. Теорема Байеса является основой механизма вывода в экспертных
системах PROSRECTOR и HULK.
Рассмотрим пример использования стратегии Байеса. Пусть требуется провести
дифференциальную диагностику между заболеваниями D
1
, D
2
, ..., D
n
. Для простоты, пусть
имеется три заболевания и четыре признака, по которым должен быть составлен диагноз.
Заболевания:
D
1
- тетрадаФалло, D
2
- дефект межпредсердечной перегородки, D
3
- незараценный
артериальный проток.
Признаки:
S
1
- цианоз, S
2
- усиление легочного рисунка, S
3
- акцент II тона во втором
межреберье слева, S
4
- правограмма (ЭКГ).
Допустим, известны следующие условные и безусловные вероятности (табл. 1.2),
полученные на основе накопленной статистики о больных данными заболеваниями.
1.2Таблица
D
j
P(D
j
) P(S
1
/D
j
) P(S
2
/D
j
) P(S
3
/D
j
) P(S
4
/D
j
)
D
1
0,35 0,9 0 0,05 0,6
D
2
0,15 0,15 0,8 0,8 0,8
D
3
0,50 0,10 0,95 0,90 0,10
Пусть у пациента налицо все четыре признака: S
1
, S
2
, S
3
, S
4
. Каков диагноз
заболевания? На основе теоремы Байеса можно оценить апостериорные вероятности
заболеваний в предположении, что признаки S
1
, S
2
, S
3
, S
4
независимые. Найдем
P = P(D |S , S , S , S ),
1 1 1 2 3 4
P = P(D |S , S , S , S ), P = P(D |S , S , S , S ):
2 2 1 2 3 4 3 3 1 2 3 4
P(D |S , S , S , S ) =
P(D ) P(S , S , S , S |D )
P(D ) P(S , S , S , S |D )
i 1 2 3 4
i 1 2 3 4 i
j 1 2 3 4 j
j=1
4
(1.32)
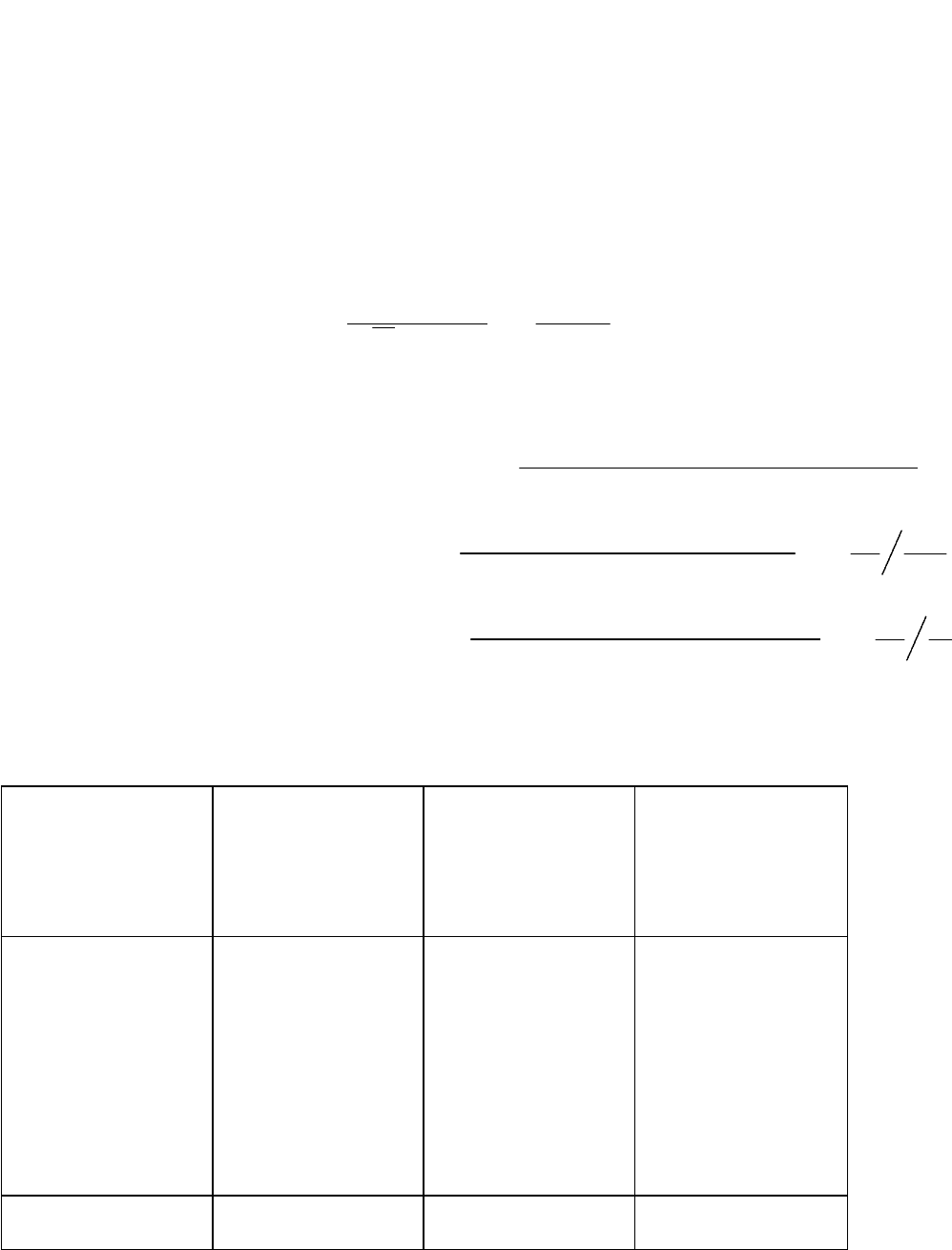
Из условия независимости признаков имеем:
P(S
1
, S
2
, S
3
, S
4
|D
i
) = P(S
1
|D
i
) P(S
2
|D
i
) P(S
3
|D
i
) P(S
4
|D
i
) (1.32)
P = 0, P = 0.73, P = 0.27.
1 2 3
Рассмотрим другой пример с шансами для оценки дождя на другой день, если
сегодня сырой, облачный, ветренный сентябрьский день. Предположим имеется
некоторая статистика, собранная по сентябрьским дням и сведенная в таблицу 1.3.
Оценим априорные шансы дождя на следующий день:
О(дождь) =
Р(дождь)
Р(не_ дождь)
=
53
173-53
= 0.44
Теперь вычислим отношения правдоподобия с учетом свидетельств:
ОП(дождь_ завтра: сырой_ день) =
Р(сырой_ день:дождь_ завтра)
Р(сырой_ день:не_ дождь_ завтра)
=
35
53
18
120
= 4.4
ОП(дождь_ завтра: облака) =
Р(облака дождь_ завтра)
Р(облака не_ дождь_ завтра)
=
8
53
= 0.67
27
120
ОП(дождь_ завтра: ветрено) =
Р(ветрено: дождь_ завтра)
Р(ветрено:не_ дождь_ завтра)
=
7
53
= 0.66
24
120
Таблица 1.3
Фактор,
характеризующий
текущий день
Значение
Число
наблюденных
дождливых
следующих дней
Число
наблюденных не
дождливых
следующих дней
Влажность высокая
средняя
умеренная
35
12
6
_____
53
18
42
60
_____
120
Ясность ясно 5 83

пасмурно
8
40
_____
53
27
10
_____
120
Ветренность слабая
средняя
сильная
19
27
7
_____
53
52
44
24
_____
120
Примечания: 1) общее число наблюденных сентябрьских дней - 173;
2) число дождливых дней - 53.
Далее, используя формулу (1.31), находим
О(дождь_завтра*) = 0.44 4.4 0.67 0.66 = 0.856
и с помощью формулы (1.29) рассчитываем вероятность дождя завтра, если сегодня
облачная, сырая и ветреная погода:
Р(дождь_ завтра*) =
0.856
1.856
= 0.46
Таким образом, байесовская стратегия позволяет корректировать вероятность
гипотезы с учетом известных факторов.
1.2.3 Как функционирует машина вывода
Машина вывода является интерпретатором правил, который использует факты базы
знаний для решения проблем. На входе машина вывода получает цель консультации.
На каждом шаге вывода машина вывода строит (наращивает) контекст (трассу
вывода) и пытается подобрать правило, применимое к этому контексту. Контекст - это
математическая структура, соответствующая образцу (см. предыдущий параграф),
которому дополнительно придана цель вывода. При этом цель вывода может также
задаваться в виде образца-цели.
Изменение контекста реализуется либо вследствие применения правил вывода,
либо путем ввода фактов, запрашиваемых у пользователя. Например, пусть цель
