Лекции - Архитектура систем искусственного интеллекта

Подождите немного. Документ загружается.

a) переменные, обозначаемые через x, y, z, v, u, ...,

b) константы, обозначаемые посредством a, b, c, d, ...,

c) функциональные символы, представляемые как f, g, h, ...,

d) символы отношений p, q, r, s, ...,

e) символы пропозициональных констант: TRUE (истина) и FALSE (ложь)

f) логические операторы (связки): - (отрицание, НЕ),  (дизъюнкция, ИЛИ), &

(конъюнкция, И),  ( импликация, ЕСЛИ ...ТО),  ( эквиваленция, ЕСЛИ И

ТОЛЬКО ЕСЛИ)

g) кванторы:  (существование),  (всеобщности)

h) круглые скобки (,) и запятую ",".

Для конъюнкции используется также символ , а для эквиваленции  или .

Каждый символ функции и отношения характеризуется числом аргументов данной

функции (отношения) называемым местностью (арностью). Например, функция sin(х)

является одноместной, f(x

, x, c) - трехместной и т.п.

Далее определим класс термов:

а) переменная есть терм;

b) константа есть терм;

с) если f есть n - местная функция и t

, ..., t

- термы, f(t

, ..., t

) суть также терм.

Логическая формула задается следующей схемой:

a) если p - n - местное отношение и t

, ..., t

- термы, то p(t

, ..., t

) есть формула

(называемая атомарной)

b) пропозициональные константы TRUE и FALSE суть формулы

c) если F и G формулы, то формулами также являются (

), (F  G), (F & С), (F  С),

(F  С)

d) если F - формула и х - переменная, то ( х F ) и ( х Р ) - также формулы.

Для упрощения записи логических формул часто отбрасывают скобки, используя

отношение порядка (старшинства) между логическими операторами и кванторами. Так,

будем считать, что -, ,  связывают сильнее, чем &, который в свою очередь связывает

сильнее оператора , а последний связывает сильнее, чем операторы , .

Поэтому формулу

(



y (



x ((p(x) & (

(y)))



(

(x)



B))))) (1.3)

можно представить в виде



y (



x (p(x) & (

(y))



(x)



B) (1.4)

Рассмотрим, как представляются знания о предметной области на основе

логических формул. Предложение: " Для всех х, если х студент, то сдает экзамены х "

может быть представлено как

x (P(x)  Q(x)),

где Р - эквивалентно Студент;

Q - эквивалентно Сдает-экзамены.

Следовательно, в эквивалентной нотации, можно записать

x (Студент (x)  Сдает-экзамены (x)).

Предложение: "Только артисты восхищаются артистами" получает представление в

виде:

 x  y (B(y, x) & A(x)  A(y)),

где А(х) - "x есть артист", В(у, х) - "у восхищается х".

Утверждение ассоциативности арифметической операции сложения имеет

следующее формальное представление:

 x  y  z ((x +y) + z = x + (y + z))

Отметим, что последнее выражение с точки зрения правил построения формул

логики предикатов следовало записать в виде:

 x  y  z E ((fadd(fadd(x, y), z) fadd(x, fadd(y, z)))),

где Е - предикат равенства ( = );

fadd - двухместная функция сложения;

fadd (t

, t

) - терм, представляющий сумму термов t

и t

Как видим, последнее представление значительно менее наглядное.

Отличительными чертами логических моделей являются единственность

теоретического обоснования и возможность реализации системы формально точных

определений и выводов. Основными задачами, решаемыми на логических моделях,

являются следующие:

 установить или опровергнуть выводимость некоторой формулы (в общем случае

эта задача алгоритмически неразрешима);

 доказательство полноты/неполноты некоторой формально логической системы,

представленной множеством логических формул;

 установление выполнимости системы логических формул (нахождение

интерпретирующей функции) или отыскание контрпримера, опровергающего

их;

 определение следствий из заданной системы формул;

 доказательство эквивалентности двух формально-логических систем;

 поиск решения задачи на основе доказательства теоремы существования

решения и др.

1.1.3 Модели знаний на основе продукций

В модели знаний на основе продукций знания представлены совокупностью

правил в формате "ЕСЛИ - ТО". Рассмотрим, например, правила порождения

родительного падежа слов, задаваемые таблицей 1.1.

Для того, чтобы получить родительный падеж слова "Знахарь" отыскиваем первую

подходящую строку, начиная с верхней, в левом колонке табл.1.1. Строка будет

подходящей, если указываемое в ней окончание совпадает с окончанием слова (в данном

случае выбирается строка 5). Нетрудно, однако видеть, что строка 6 также подходит для

нашей цели, хотя выдаваемый ею результат (правая колонка табл. 1.1.) не верен. Прежде

чем мы рассмотрим более подробно это свойство системы продукций, выясним их

природу. Рассматривая структуру продукции, нетрудно видеть, что ее условная часть

("ЕСЛИ...") определяет ситуацию, в которой продукция применима. В примере со словом "

знахарь" ситуация определяется его окончанием, т.е. либо окончанием "арь", либо ''-ь".

Таблица 1.1.

№ п/

Слово или его окончание в

именительном падеже

Слово или его окончание в

родительном падеже

1. кино -кино

2. -ча -чи

3. -ка -ки

4. -а -ы

5. -арь -аря

6. -ь -и

7. -ие -ия

8. -мя -мени

9. -я -и

Если ситуация удовлетворяет продукции, то в результате ее применения может

быть получен новый объект (состояние) согласно части " ТО ... " в структуре продукции.

Так, применение продукции с номером 5 в табл.1.1. к слову "знахарь" порождает слово

"знахаря", а применение продукции номер 6 дает слово "знахари". Таким образом,

одним из основных вопросов в реализации продукционных систем является стратегия

выбора альтернативных правил. В общем случае эта проблема нетривиальна. Условная

часть продукции может иметь различные формы, такие например, как в следующих

примерах:

 ЕСЛИ (идет - дождь) ;

 ЕСЛИ (a > b

- b) ;

 ЕСЛИ (P C Q) .

В структуре продукции дополнительно могут указываться метка и строка,

содержащая объяснение применения продукции. Метка может быть простым

идентификатором (или номером) или некоторым пояснительным текстом, например,

"определение окраски инфекции по Граму" Строка-объяснение показывает, почему

используется продукция. Следующий пример демонстрирует полную продукцию:

МЕТКА: R26 Использование зонтика

УСЛОВИЕ: ЕСЛИ (идет дождь)

ДЕЙСТВИЕ: ТО (возьмите зонтик)

ОБЪЯСНЕНИЕ: (зонтик предохраняет от дождя)

Как правило, задача, формулируемая для продукционной системы, имеет одну из

следующих структур

, S

- ?> (1.5)

- ?, S

> (1.6)

, S

, A - ?> (1.7)

, S

- ?, A - ?> (1.8)

где: S

- начальная ситуация

- конечная (желаемая, требуемая ситуация)

А - алгоритм (последовательность выполняемых продукций), переводящий систему

из состояния S

в состояние S

Задача (1.5) связана с определением ситуации (состояния) S

, удовлетворяющей

некоторому критерию, которая может быть получена из заданной

начальной ситуации.

Задача (1.6) является обратной по отношению к предыдущей.

Задача (1.7) заключается в отыскании алгоритма преобразования начальной

ситуации в конечную.

Задача (1 .8) представляет обобщение задач (1 .5) и (1 .7).

Продукции удачно моделируют человеческий способ рассуждений при решении

проблем. Поэтому продукции широко используются во многих действующих ЭС. Система

MYCIN, фрагмент которой приведен во введении, а также ее более поздняя редакция

EMYCIN являются примерами продукционных систем.

Продукционные системы впервые изобретены Постом в 1941г. Продукция в системе

Поста имеет следующую схему

t t . . . t

1 2 n

(1.9)

где t

, t

, ..., t

называются посылками, а t заключением продукции.

Применение схемы (1.9) основывается на подстановке цепочек знаков вместо всех

переменных, причем вместо вхождений одной и той же переменной подставляется одна и

та же цепочка.

В качестве других классических продукционных систем отметим нормальные

алгоритмы Маркова и машину Тьюринга.

Развитием модели на основе правил является модель "доски объявлений". Эта

модель реализована в системе распознавания разговорной речи HEARSAY - 2. Основной

принцип организации модели доски объявлений заключается в разбиении продукций по

уровням иерархии. При этом заключения продукций на нижних уровнях используются как

входные условия для продукций более высокого уровня. На самом нижнем уровне

модели доски объявлений представлены факты, на самом верхнем - результирующее

заключение.

Иерархическое разбиение множества продукций позволяет более эффективно

организовать их выполнение, существенно сократив затраты на перебор множества

продукций при проверке условий их срабатывания, что определяет дополнительный

интерес к продукционным системам.

В рамках этой модели продукция определяется четверкой:

P = < L, C, N, A >,

где L – метка;

С – условие применимости;

N – ядро продукции, описываемое формулой (1.9);

А – постдействие.

В качестве примера составления системы продукций рассмотрим задачу

распознавания символов, в которой введем следующие упрощения: будут исследованы

прописные буквы Кириллицы. В примере будем использовать структурный метод. Этот

метод заключается в структуризации всех символов по определенным признакам.

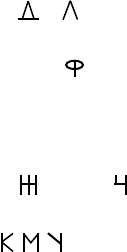
Приведем алфавит:

: А И Х

: Б З Р Ы Ь Я В

: С О Э Ю

: Е Н П Т Ш Г

: Ц Ъ Щ

Данный алфавит был разделен на группы, исходя из внутреннего строения каждого

символа.

Таким образом получено следующее множество:

’ – вертикальные наклонные (отвесные) прямые;

’ – горизонтальные прямые;

’ – полуовалы;

’ – большие овалы;

’ – вертикальные прямые;

’ – короткие вертикальные наклонные отрезки;

’ – хвостики.

Данная продукция может быть представлена в виде:

P = < L, C, N, A >, где L=L

, а С – условие применимости данного шрифта.

’ f

’

















654321

PPPP

PPP

GGGGGG

ffff

fff

Постдействие А определяет процедуру, которая может либо вызывать продукцию

для определения буквы найденного класса, либо выставлять на доску объявлений

сообщения о том, что найдена группа, которой принадлежит исследуемая буква и

передается номер этой буквы.

На языке Prolog такая продукция выглядит так:

:–G

:–P

f1’

, P

f2’

, P

f5’

……………

Для распознавания буквы в группе можно все факты представить следующим

образом:

– кривая замкнутая полная (на высоту кадра);

– кривая с левосторонней выпуклостью;

– кривая с правосторонней выпуклостью;

– кривая верхняя с правосторонней выпуклостью;

– кривая верхняя с левосторонней выпуклостью;

– кривая нижняя с правосторонней выпуклостью;

– кривая нижняя с левосторонней выпуклостью;

– вертикальный левый отрезок;

– вертикальный правый отрезок;

– вертикальный центральный отрезок;

– вертикальный левый верхний отрезок;

– вертикальный левый нижний отрезок;

– вертикальный правый верхний отрезок;

– вертикальный правый нижний отрезок;

– вертикальный центральный верхний отрезок;

– вертикальный центральный нижний отрезок;

– вертикальный отрезок с углом наклона менее 90;

– вертикальный отрезок с углом наклона более 90;

– вертикальный верхний отрезок с углом наклона менее 90;

– вертикальный верхний отрезок с углом наклона более 90;

– вертикальный нижний отрезок с углом наклона менее 90;

– вертикальный нижний отрезок с углом наклона более 90;

– горизонтальный верхний отрезок;

– горизонтальный нижний отрезок;

– горизонтальный центральный отрезок;

– хвостик.

Рассмотрим символы из второй группы.

Б З Р Ф Ы Ь Я В



















fff

ВЯЬЫФРЗБ

PPP

PPPPPPPP

648

2368

Постдействием для такой продукции будет процедура помещения распознанной

буквы в какую-либо базу данных.

1.1.4 Фреймовая модель знаний

Фреймовая модель знаний предложена Марвином Минским. Минский также ввел

терминологию и язык фреймов. Эта терминология включает такие понятия как "фреймы",

"слоты", "терминалы", "значения по умолчанию". Фрейм определяется как структура

следующего вида:

{<имя-фрейма> <имя слота

> <значение слота>

, ...,

<имя слота

> <значение слота>

}

Так, определим фрейм для объекта "книга":

{<КНИГА>

<АВТОР> <ДюмаА.>

<НАЗВАНИЕ> <Граф Мосте Кристо>

<ЖАНР> <Роман>}

Мы видим, что слоты соответствуют атрибутам (характеристикам, свойствам)

объекта. Если значения слотов не определены, то фрейм называется фреймом-

прототипом. Заменяя неизвестное значение звездочкой ("*") будем иметь следующий

фрейм-прототип:

{<КНИГА>

<АВТОР> <*>