Лекции - Аэродинамика и вентиляция. Часть 1
Подождите немного. Документ загружается.


АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
41
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
Лекция 7 – Динамика давлений в воздуховодах.
[2,
с
.172-177]
Характеристика
вентиляционной
сети
Эпюры
давлений
в
сети
воздуховодов
Характеристика
вентиляционной
сети
В
соответствии
с
выражением
(6.1)
потери
давления
на
участке
воздуховода
равны
:
2
2
2
2
2
2
4
2
4
22
Q
dd
l
d
Q
d
lv
d
l
p
эээ
⋅
⋅
+=
⋅
+=
+=∆
∑∑∑
π
ρ
ζλ
π
ρ
ζλ
ρ
ζλ
. (7.1)
Если
величины
λ
и
Σζ
не
зависят
от
числа
Рейнольдса
,
т
.
е
.
от
v
и
d,
то
:
const
dd
l
э
=
⋅
+
∑
2
2
4
2
π
ρ
ζλ
.
И
тогда
для
всего
воздуховода
будет
справедлива
зависимость
:
2
Qkp
⋅=∆
. (7.2)
С
учетом
режима
течения
потока
следует
эту
зависимость
записать
в
виде
:
n
Qkp
⋅=∆
. (7.3)
Причем
для
ламинарного
режима
движения
n = 1,
а
для
турбулентного
– n = 1,75…2,0 (
меньшая
величина
для
гладких
,
а
большая
–
для
шероховатых
воздуховодов
).
Величина
k
носит
название
коэффициент гидроаэродинамического сопротивления
.
Значение
k
определяется
геометрическими
и
физическими
характеристиками
сети
воздуховодов
(
протяженность
,
форма
и
размеры
поперечных
сечений
,
шероховатость
стенок
),
наличием
мест
-
ных
сопротивлений
и
физическими
свойствами
перемещаемого
потока
(
плотность
,
кинематиче
-
ская
вязкость
).
Чем
протяженнее
и
сложнее
сеть
,
тем
величина
коэффициента
k
больше
.
В
самом
общем
случае
зависимость
(7.2)
записывается
в
виде
:
2
0
Qkpp ⋅+=∆
. (7.4)
где
: p
0
–
аэростатическая
составляющая
давления
.
Уравнение
(7.4)
называют
характеристикой сети воздуховодов
(
характеристикой
сети
).
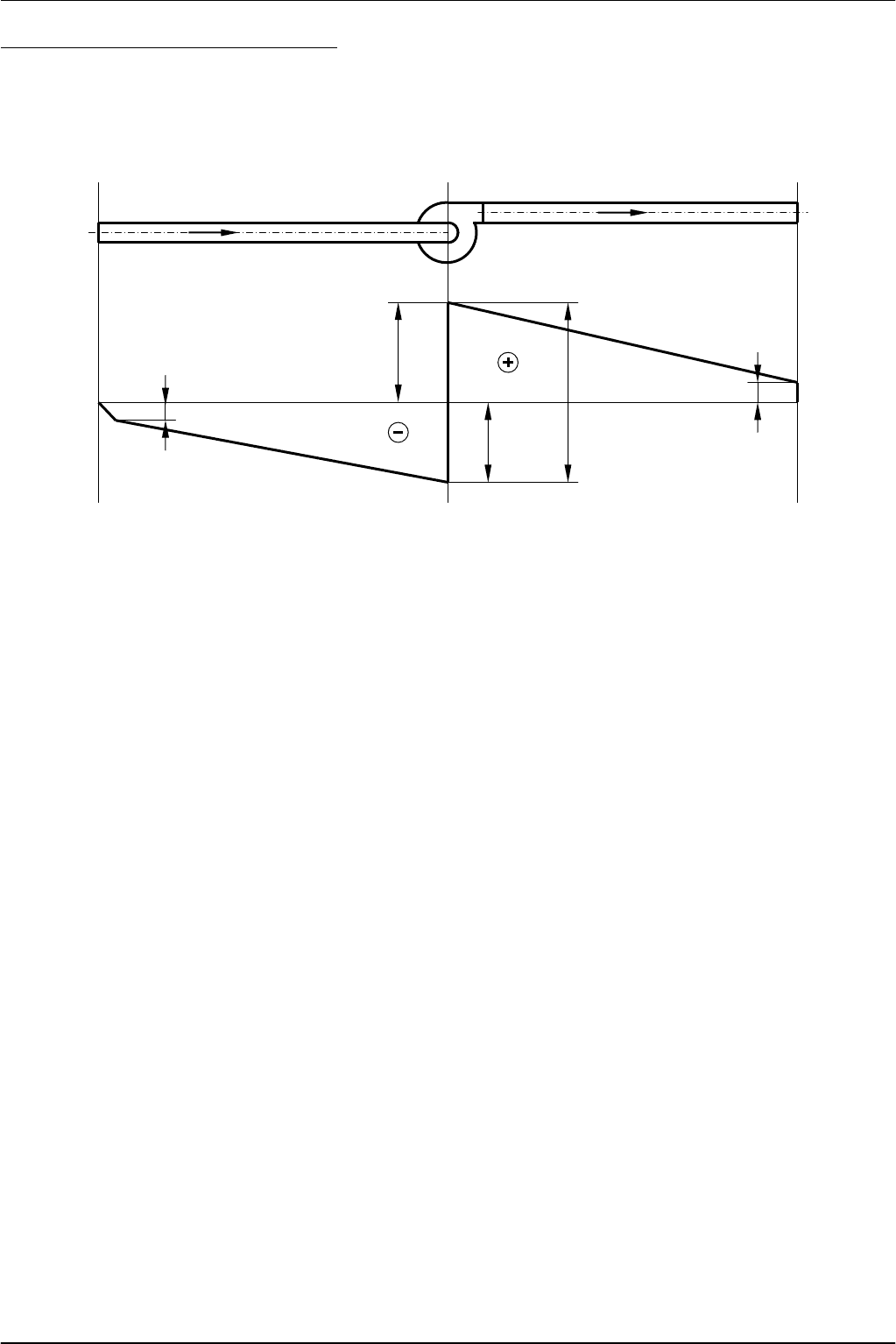
Если
по
уравнению
(7.4)
построить
характеристику
сети
воздуховодов
и
в
этой
же
системе
ко
-
ординат
нанести
характеристику
вентилятора
(
рисунок
7.1),
то
точка
пересечения
этих
двух
кри
-
вых
характеризует
режим
работы
системы
вентилятор
-
сеть
и
называется
рабочей точкой
.
При
помощи
характеристики
сети
можно
определить
расход
воздушного
потока
в
сети
для
со
-
ответствующих
потерь
давления
,
и
,
наоборот
,
потери
давления
для
заданного
расхода
.
Q
,
м
3
/
ч
p,
Па
0
p
0
Характеристика
вентилятора
Характеристика
сети
∆
p=kQ
2
∆
p=p
0
+kQ
2
Рабочая точка
Рис
. 7.1
АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
42
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
Эпюры
давлений
в
сети
воздуховодов
Работа
вентилятора
в
сети
воздуховодов
становится
понятной
,
если
проанализировать
распре
-
деление
давлений
в
системе
путем
построения
эпюр
давлений
.
Рассмотрим
простую
систему
вентиляции
,
которая
состоит
из
вентилятора
,
всасывающего
и
на
-
гнетательного
воздуховодов
(
рисунок
7.2).
Давление
в
начале
и
в
конце
системы
равно
атмосфер
-
ному
давлению
.
В
плоскости
всасывающего
отверстия
полное
давление
потока
равно
нулю
.
Давление
непосредственно
перед
входом
в
вентилятор
Р
вс
меньше
давления
среды
при
входе
в
систему
(
разряжение
–
на
эпюре
откладывается
вниз
)
и
равно
потерям
давления
во
всасывающем
воздуховоде
.
Давление
непосредственно
за
плоскостью
всасывающего
отверстия
воздуховода
определяется
потерей
давления
при
входе
воздушного
потока
в
открытый
торец
трубопровода
∆Р
вх
.
Давление
непосредственно
за
вентилятором
(
избыточное
давление
–
на
эпюре
откладывается
вверх
)
равно
потерям
давления
в
нагнетательном
воздуховоде
.
В
сечении
выхода
в
атмосферу
дав
-
ление
равно
потерям
давления
при
выходе
потока
из
отверстия
в
неограниченное
пространство
(
ζ
= 1),
т
.
е
.
динамическому
давлению
вытекающей
воздушной
струи
Р
д.вых
.
Аналогично
рассмотренной
выше
эпюре
полного
давления
можно
построить
эпюры
динамиче
-
ского
и
статического
давлений
.
Динамическое
давление
как
во
всасывающем
,
так
и
в
нагнетательном
воздуховодах
имеет
по
-
ложительное
значение
(
это
вытекает
из
самого
определения
динамического
давления
как
меры
кинетической
энергии
потока
).
Действительно
,
в
соответствии
с
формулой
2/
2
vp
д
ρ
=
динами
-
ческое
давление
может
принимать
либо
положительные
значения
,
либо
0 (
в
случае
,
когда
v = 0).
Как
было
показано
выше
,
полное
давление
во
всасывающем
воздуховоде
–
отрицательно
,
в
на
-
гнетательном
–
положительно
.
Статическое
давление
найдем
из
соотношения
:
p
ст
= p
п
- p
д
.
Учитывая
все
вышесказанное
,
можно
заключить
,
что
для
рассматриваемой
простой
вентиляци
-
онной
системы
во
всасывающем
воздуховоде
статическое
давление
будет
иметь
отрицательные
значения
(
т
.
к
. p
п
–
величина
отрицательная
,
а
p
д
–
положительная
),
а
в
нагнетательном
может
при
-
нимать
как
положительные
(
в
случае
,
если
p
п
> p
д
),
так
и
отрицательные
(
в
случае
,
если
p
п
< p
д
)
значения
.
В
выходном
сечении
(
выход
воздуха
в
атмосферу
)
статическое
давление
считается
равным
0.
Пример
.
Построить
эпюры
полного
,
динамического
и
статического
давлений
для
системы
вен
-
тиляции
(
рисунок
7.3)
по
таким
данным
: Q = 720
м
3
/
ч
= 0,2
м
3
/
с
;
ρ
= 1,2
кг
/
м
3
; F
1
= F
2
=
F
3
= 0,02
м
2
; F
4
= 0,04
м
2
.
Суммарные
потери
давления
во
всасывающем
воздуховоде
∆
p
вс
= 100
Па
,
в
нагнета
-
тельном
воздуховоде
∆
p
наг
= 100
Па
(
из
них
50
Па
после
сечения
3-3).
Результаты
расчетов
давлений
в
сечениях
,
выполненных
по
формулам
:
Р
нагн
Р
вс
Р
Р
д.вых
Рис
. 7.2
∆Р
вх
АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
43
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
p
ст
= p
п
- p
д
;
2/
2
vp
д
ρ
=
; v = Q/F; (p
п
)
i
= (p
п
)
i+1
+
∆
p
(i)-(i+1)
,
сводим
в
таблицу
7.1.
Таблица
7.1
Сечение
Расчетная величина
0-0 1-1
2-2
всасывание
2-2
нагнетание
3-3 4-4
v,
м
/
с
0 10 10 10 10 5
p
д
,
Па
0 +60 +60 +60 +60 +15
p
ст
,
Па
0 -60 -160 +90 -10 0
p
п
,
Па
0 0 -100 +150 +50 +15
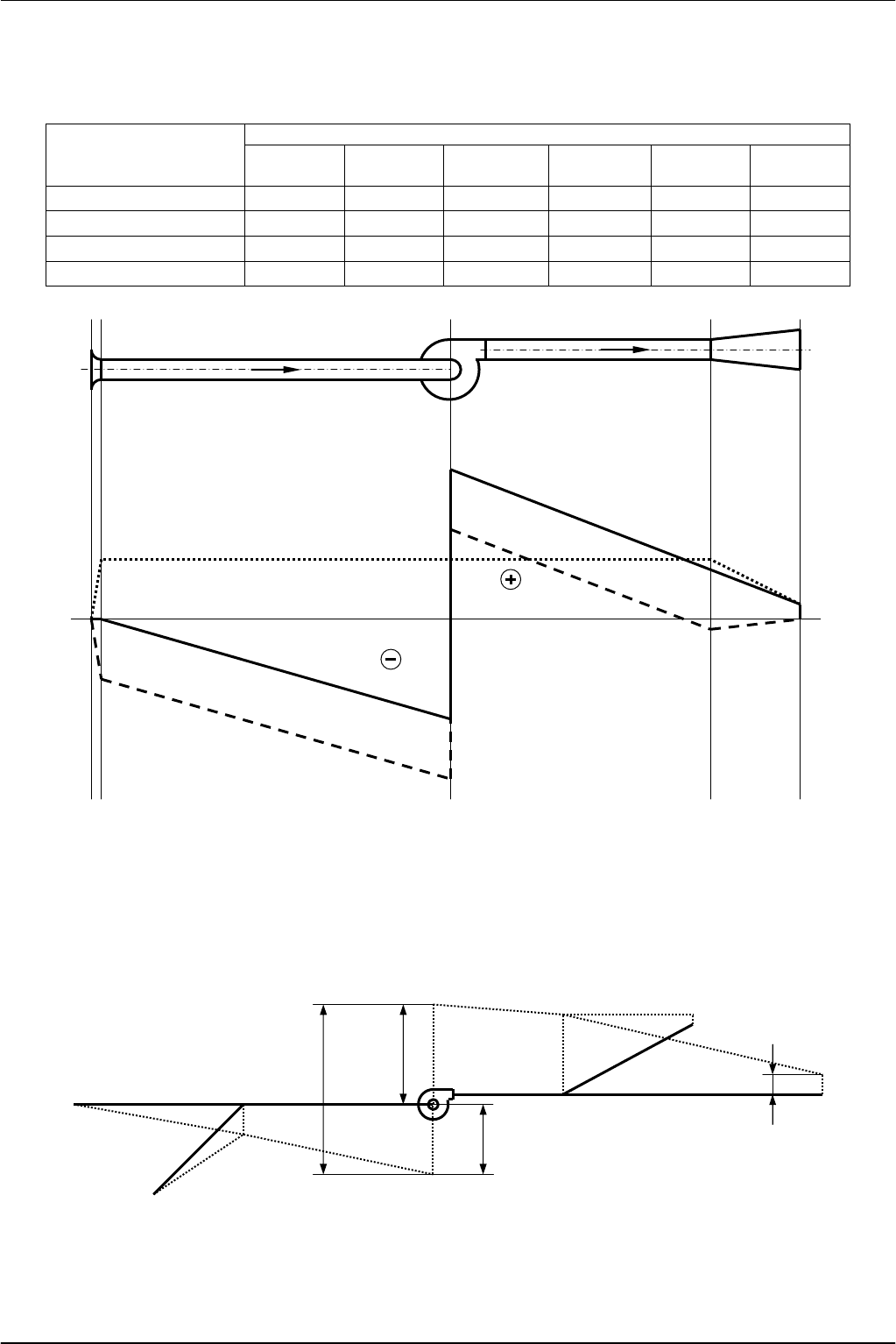
Анализ
полученных
эпюр
показывает
,
что
перед
диффузором
в
нагнетательном
воздуховоде
(
сечение
3-3)
статическое
давление
отрицательно
(
меньше
атмосферного
).
Это
значит
,
что
через
отверстие
,
сделанное
в
этом
месте
нагнетательного
воздуховода
,
воздух
будет
подсасываться
из
окружающей
среды
потоком
,
который
движется
в
воздуховоде
(
а
не
вытекать
из
воздуховода
).
Аналогично
можно
построить
эпюры
давлений
в
разветвленных
воздуховодах
,
учитывая
усло
-
вия
равенства
полных
давлений
в
узлах
системы
(
рисунок
7.4).
∆
P
вс
,
∆
P
наг
–
суммарные
потери
давления
на
всасывании
и
нагнетании
соответственно
;
P
д.вых
–
динамическое
давление
на
выходе
воздуха
из
системы
;
P
в
–
полное
давление
,
развиваемое
вентилятором
.
Рис
. 7.3
Р
ст
0
0
1
1
2
2
3
3
4
4
Р
п
Р
д
0
60
-60
-160
-100
60
-10
90
150
15
Р
п
Рис
. 7.4
∆
P
вс
∆
P
наг
P
в
P
д.вых

АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
44
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
Лекция 8 –Аэродинамика двухфазных потоков.
[1,
с
.59-66; 2,
с
.101-113, 159-170]
Аэродинамические
сила
и
момент
Коэффициент
силы
лобового
сопротивления
Скорости
витания
и
трогания
Расчет
воздуховодов
для
двухфазных
потоков
(
системы
аспирации
и
пневмотранс
-
порта
)
Аэродинамические
сила
и
момент
При
обтекании
тела
потоком
на
каждую
элементарную
площадку
его
поверхности
воздейству
-
ют
силы
давления
и
трения
.
Сложение
этих
сил
(
по
правилу
параллелограмма
)
в
самом
общем
случае
,
как
известно
из
теоретической
механики
,
приведет
к
главному
вектору
R
и
главному
мо
-
менту
М
(
рисунок
8.1).
В
аэродинамике
главный
вектор
называют
аэродинамической силой
,
а
главный
момент
–
аэ-
родинамическим моментом
.
Пользуясь
приемом
неопределенных
коэффициентов
,
выведем
формулу
для
определения
аэро
-
динамической
силы
R
способом
анализа
размерностей
.
Очевидно
,
сила
R
зависит
от
площади
наибольшего
поперечного
сечения
тела
F,
коэффициента
кинематической
вязкости
воздуха
ν
,
плотности
воздуха
ρ
и
скорости
набегающего
потока
v
0
:
R = f(F,
ν
,
ρ
, v
0
).
Эту
неизвестную
функцию
будем
искать
в
следующем
виде
:
nzyx
vAFR
0
ρν
=
, (8.1)
где
:
А
–
безразмерный
коэффициент
;
x, y, z, n –
пока
неизвестные
показатели
степени
.
Чтобы
найти
эти
показатели
,
в
зависимость
(8.1)
вместо
величин
подставим
единицы
их
изме
-
рения
в
системе
СИ
:
( )
nz
y
x
с
м
м
кг
с
м
мН
=
3
2
2
,
или
( )
nz
y
x
с
м
м
кг
с
м
м
с
мкг
=
⋅
3
2
2
2
.
Что
дает
:
ny
nzyxz
с
мкг
с
мкг
+
+−+
⋅
=
⋅
322
2
.
Показатели
степени
у
единиц
измерения
величин
слева
должны
быть
такими
же
,
как
и
показа
-
тели
степени
у
единиц
измерения
соответствующих
величин
справа
.
С
учетом
этого
обстоятельст
-
ва
будет
справедлива
следующая
система
уравнений
:
z = 1; 2x + 2y – 3z + n = 1; y + n = 2.
Итак
,
получили
три
уравнения
с
четырьмя
неизвестными
.
Будем
считать
,
что
один
показатель
степени
,
например
n,
нам
известен
.
Тогда
,
решая
систему
относительно
n,
получим
:
z
y
x
M
R
ds
0
Рис
. 8.1
v
0

АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
45
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
x = n /2; y = 2 - n; z = 1.
Подставляя
эти
значения
x, y
и
z
в
зависимость
(8.1),
получим
:
nnn
vAFR
0
22/
ρν
−
=
. (8.2)
В
большинстве
практических
случаев
в
потоке
наблюдается
развитая
турбулентность
и
тогда
,
согласно
опытным
данным
, n = 2,
что
дает
:
2
0
vAFR
ρ
=
.
Умножив
и
разделив
правую
часть
на
2
и
обозначив
2
А
=
С
R
,
окончательно
получим
:
2
2
2
2
2
2
0
2
0
2
0
v
FC
v
AFvAFR
R
ρρ
ρ
===
. (8.3)
где
:
С
R
–
коэффициент аэродинамической силы
;
F –
площадь
наибольшего
поперечного
сечения
обтекаемого
тела
(
площадь
миделевого
се
-
чения
).
Аналогично
рассуждая
,
можно
вывести
формулу
для
аэродинамического
момента
:
2
2
0
v
FlCM
m
ρ
=
. (8.4)
где
:
С
m
–
коэффициент аэродинамического момента
;
l –
характерная
длина
.
Вследствие
того
,
что
сила
R
и
момент
M
являются
векторами
,
при
практических
расчетах
удоб
-
но
пользоваться
их
проекциями
на
прямоугольные
оси
координат
.
В
качестве
таковых
выбираются
так
называемые
поточные
оси
координат
.
Начало
координат
принимается
в
центре
тяжести
обтекаемого
тела
,
ось
x
направляется
вдоль
по
течению
,
ось
z –
вбок
(
в
горизонтальной
плоскости
),
а
ось
y –
перпендикулярно
плоскости
x0z.
Тогда
вместо
равен
-
ства
(8.3)
получим
следующие
три
равенства
:
;
2
;
2
;
2
2
0
2
0
2
0
v
FCR
v
FCR
v
FCR
zzyyxx
ρρρ
===
. (8.5)
где
: R
x
–
сила лобового сопротивления
;
R
y
–
подъемная сила
;
R
z
–
боковая сила
;
C
x
, C
y
, C
z
–
соответственно
,
коэффициенты
сил
лобового
сопротивления
,
подъемной
и
боко
-
вой
.
Аналогично
вместо
равенства
(8.4)
будем
иметь
:
;
2
;
2
;
2
2
0
2
0
2
0
v
FlCM
v
FlCM
v
FlCM
mzzmyymxx
ρρρ
===
. (8.6)
где
: M
x
, M
y
, M
z
–
проекции
аэродинамического
момента
на
оси
координат
;
C
mx
, C
my
, C
mz
–
соответственно
,
коэффициенты
этих
проекций
.
В
случае
равномерного
поля
скоростей
в
набегающем
потоке
и
симметричных
тел
,
каковыми
являются
,
например
,
пластинка
,
поставленная
перпендикулярно
потоку
,
шар
и
т
.
п
.,
силовое
взаи
-
модействие
потока
с
телом
сводится
к
одной
аэродинамической
силе
.
При
этом
эта
сила
совпадает
с
направлением
течения
,
т
.
е
.
является
одновременно
и
силой
лобового
сопротивления
.
При
неравномерном
поле
скоростей
в
набегающем
потоке
и
симметричных
телах
возникают
еще
подъемная
сила
и
аэродинамический
момент
.
Если
,
например
,
поток
горизонтален
и
скорость
увеличивается
по
оси
y,
а
тело
является
шаром
,
то
в
верхней
части
шара
скорость
воздуха
больше
,
чем
в
нижней
.
Поэтому
,
согласно
уравнению
Бернулли
,
над
шаром
давление
будет
меньше
,
чем
под
шаром
,
и
появится
подъемная
сила
.
Раз
-
ность
скоростей
в
верхней
и
нижней
частях
шара
обусловит
появление
аэродинамического
момен
-
та
.

АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
46
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
Коэффициент
силы
лобового
сопротивления
Коэффициенты
проекций
аэродинамической
силы
и
момента
определяются
экспериментально
в
потоке
с
равномерным
полем
скоростей
.
Значение
их
зависит
от
числа
Рейнольдса
.
Изменение
коэффициента
силы
лобового
сопротивления
шара
(
определенного
эксперименталь
-
ным
путем
)
в
зависимости
от
числа
Рейнольдса
представлено
на
графике
(
рисунок
8.2,
кривая
3).
При
малых
значениях
числа
Рейнольдса
(Re
≤
1)
кривая
приближенно
описывается
формулой
Стокса
(
кривая
1
на
рисунке
8.2):
Re
24
=
x
C
. (8.7)
В
несколько
большем
диапазоне
значений
числа
Рейнольдса
(Re
≤
2)
точнее
формула
Озина
(
кривая
2
на
рисунке
8.2):
+= Re
16
3
1
Re
24
x
C
. (8.8)
В
диапазоне
чисел
Рйнольдса
Re = 10÷2000
можно
пользоваться
формулой
Б
.
Лобаева
:
( )
[ ]
2
Relg
3,4
=
x
C
. (8.9)
С
увеличением
числа
Рейнольдса
коэффициент
лобового
сопротивления
уменьшается
и
при
Re = 10
3
÷10
5
достигает
значения
0,4-0,48.
Затем
при
дальнейшем
увеличении
Re (
примерно
от
10
5
до
4·10
5
)
значение
коэффициента
C
x
резко
уменьшается
до
0,2.
Эта
зона
падения
сопротивления
носит
название
критической
.
Критическая
зона
связана
с
переходом
пограничного
слоя
шара
из
ламинарного
состояния
в
турбулентное
.
Таким
образом
,
при
переходе
пограничного
слоя
из
лами
-
нарного
режима
в
турбулентный
коэффициент
лобового
сопротивления
резко
уменьшается
.
Такая
зависимость
коэффициента
лобового
сопротивления
характерна
для
шара
,
цилиндра
и
других
тел
,
имеющих
округлую
форму
.
Однако
для
тел
плавного
профиля
(
каплеобразный
профиль
,
крыло
самолета
и
др
.),
во
время
обтекания
которых
не
происходит
отрыва
пограничного
слоя
,
коэффициент
лобового
сопротивле
-
ния
уменьшается
постепенно
с
увеличением
критерия
Рейнольдса
.
Для
тел
плохо
обтекаемой
формы
и
инерционным
отрывом
пограничного
слоя
(
например
,
зда
-
ний
),
коэффициент
лобового
сопротивления
C
x
практически
не
зависит
от
числа
Рейнольдса
и
счи
-
тается
постоянной
величиной
.
Скорости
витания
и
трогания
Как
известно
,
при
пневматическом
транспортировании
твердых
примесей
скорость
воздуха
в
воздуховодах
должна
быть
больше
скорости
витания
и
трогания
с
тем
,
чтобы
примеси
можно
бы
-
ло
перемещать
в
вертикальных
воздуховодах
вверх
и
в
случае
их
оседания
на
дне
горизонтальных
воздуховодов
стронуть
с
места
.
Рис
. 8.2
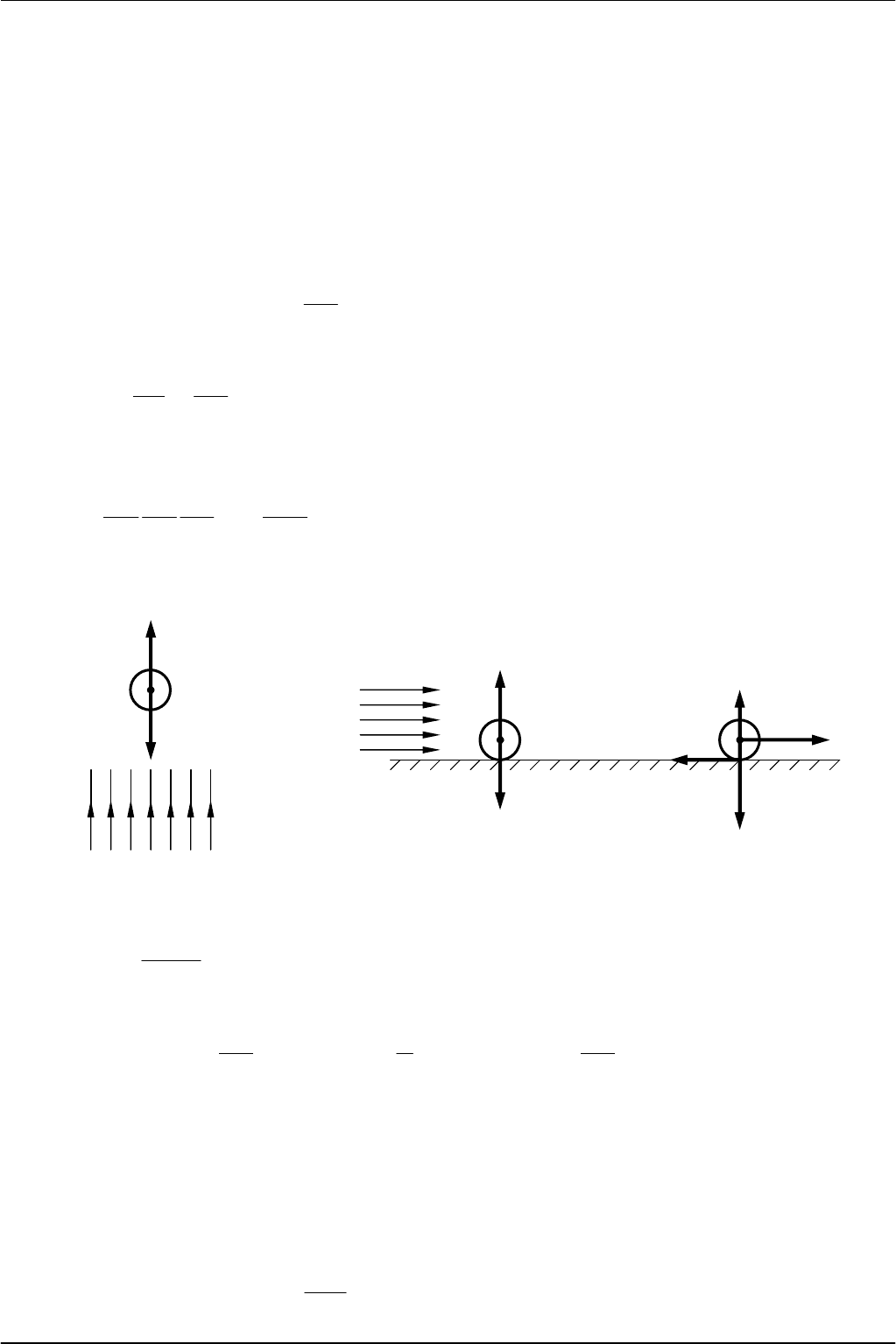
АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
47
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
Рассмотрим
,
как
при
помощи
законов
аэродинамики
устанавливаются
зависимости
для
этих
двух
скоростей
.
Вначале
установим
зависимость
для
скорости
витания
.
Пусть
на
тело
весом
Mg (M –
масса
тела
)
набегает
поток
воздуха
,
двигающийся
снизу
вверх
с
такой
скоростью
v
в
,
что
тело
не
поднимается
и
не
опускается
,
а
находится
на
одном
и
том
же
уровне
,
как
бы
повисает
в
воздухе
(
рисунок
8.3,
а
).
При
этом
оно
может
перемещаться
в
горизон
-
тальной
плоскости
под
действием
подъемной
и
боковой
сил
.
Скорость
,
при
которой
это
происхо
-
дит
,
называется
скоростью витания
.
Очевидно
,
эта
скорость
определяется
из
условия
,
что
сила
лобового
сопротивления
равна
весу
тела
:
R
x
= Mg,
или
Mg
v
FC
x
=
2
2
0
ρ
.
Учитывая
,
что
C
x
= f
x
(Re),
получаем
:
Mg
v
F
dv
f
в
x
=
2
2
0
ρ
ν
. (8.10)
Из
этого
уравнения
,
если
известна
функция
f
x
,
можно
определить
скорость
витания
.
В
частном
случае
для
шара
диаметром
d
при
Re
≤
1
имеем
C
x
= 24/Re,
и
тогда
:
g
dvd
dv
м
в
в
3
4
24
24
322
π
ρ
ρπν
=
,
где
:
ρ
м
–
плотность
материала
шара
.
Из
последнего
уравнения
следует
,
что
скорость
витания
равна
:
ρν
ρ
18
2
gd
v
м
в
=
. (8.11)
Если
скорость
воздуха
v > v
в
,
то
тело
начнет
двигаться
вверх
со
скоростью
v
т
,
равной
:
dt
dv
MMgR
т
x
=−
,
или
( )
dt
dv
MMgvvFC
т
т
x
=−−
2
2
ρ
.
Установим
теперь
зависимость
для
скорости
трогания
.
Ввиду
сложности
вопроса
аэродинами
-
ческий
момент
будем
полагать
равным
нулю
.
Пусть
на
тело
весом
Mg,
лежащее
на
горизонтальной
плоскости
,
набегает
горизонтальный
по
-
ток
воздуха
с
такой
скоростью
,
что
тело
поднимается
в
воздух
или
скользит
по
плоскости
по
на
-
правлению
течения
(
рисунок
8.3,
б
,
в
).
В
первом
случае
Mg = R
y
и
,
очевидно
,
скорость
трогания
будет
определяться
из
условия
,
что
подъемная
сила
равна
силе
тяжести
(
рисунок
8.3,
б
):
R
y
= Mg,
или
Mg
v
FC
тр
y
=
2
2
ρ
.
R
x
Mg
v
а
)
R
y
Mg
R
y
Mg
R
x
T
v
б
)
в
)
Рис
. 8.3

АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
48
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
Учитывая
,
что
C
x
= f
y
(Re),
можем
написать
:
Mg
v
F
dv
f
тртр
y
=
2
2
ρ
ν
. (8.12)
Из
этого
уравнения
,
если
известна
функция
f
y
,
можно
определить
скорость
трогания
.
Если
скорость
воздуха
v > v
тр
,
то
тело
начнет
двигаться
со
скоростью
v
т
,
равной
:
dt
dv
MMgR
т
y
=−
,
или
( )
dt
dv
MMgvvFC
т
т
y
=−−
2
2
ρ
.
Во
втором
случае
Mg > R
y
(
см
.
рисунок
8.3,
в
)
и
,
скорость
трогания
определяется
из
условия
,
что
сила
лобового
сопротивления
равна
силе
трения
R
x
= T
или
:
R
x
= (Mg - R
y
)·f,
где
: f –
коэффициент
трения
.
Отсюда
:
f
v
FCMg
v
FC
тр
y
тр
x
−=
22
22
ρρ
,
или
f
v
F
dv
fMg
v
F
dv
f
тртр
y
тртр
x
−=
22
22
ρ
ν
ρ
ν
. (8.13)
Из
этого
уравнения
,
если
известны
функции
f
x
и
f
y
,
можно
найти
скорость
трогания
.
Необходимо
отметить
,
что
если
скорость
витания
определяется
по
одной
зависимости
,
то
ско
-
рость
трогания
определяется
по
двум
зависимостям
.
Очевидно
,
для
скорости
трогания
первый
случай
характерен
для
легких
тел
,
а
второй
–
для
тя
-
желых
тел
.
Для
эффективного
транспортирования
твердых
частиц
необходимо
,
чтобы
скорость
потока
превышала
так
называемую
критическую
скорость
v
кр
,
т
.
е
.
такую
минимальную
скорость
потока
,
при
которой
твердые
частицы
двигаются
в
воздушном
потоке
скачкообразно
,
без
осаждения
час
-
тиц
на
стенках
воздуховода
.
Критическая скорость
зависит
от
скорости
витания
,
количества
материала
,
который
транс
-
портируется
,
его
плотности
и
концентрации
.
Для
систем
пневмотранспорта
ее
можно
определить
по
эмпирической
формуле
,
м
/
с
:
25,0
5,0
36,0
34.0
6,5 xdDv
воз
ч
чкр
⋅=
ρ
ρ
, (8.14)
где
: D
и
d
ч
–
соответственно
,
внутренний
диаметр
трубопровода
и
среднемедианный
диаметр
частиц
,
м
;
ρ
ч
и
ρ
воз
–
соответственно
,
плотности
дискретной
(
механические
примеси
)
и
сплошной
(
воз
-
душный
поток
)
фаз
в
двухфазной
системе
;
x –
расходная
концентрация
смеси
,
кг
/
кг
,
определяется
по
выражению
(8.16).
Расчет
воздуховодов
для
двухфазных
потоков
(
системы
аспирации
и
пневмотранспорта
)
Одними
из
важнейших
характеристик
двухфазных
потоков
являются
объемная
концентрация
β
и
расходная
концентрация
x.
Объемная концентрация
характеризует
отношение
объема
,
который
занимает
дискретная
фа
-
за
,
к
общему
объему
двухфазной
системы
:
чвоз
ч
WW
W
+
=
β
, (8.15)
где
: W
ч
и
W
воз
–
соответственно
,
объемы
дискретной
(
механические
примеси
)
и
сплошной
(
воз
-
душный
поток
)
фаз
в
двухфазной
системе
.

АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
49
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
Расходная концентрация
x
характеризует
отношение
массового
расхода
дискретной
компо
-
ненты
к
массовому
расходу
смеси
:
чвоз
ч
GG
G
x
+
=
, (8.16)
где
: G
ч
и
G
воз
–
соответственно
,
массовые
расходы
дискретной
(
механические
примеси
)
и
сплош
-
ной
(
воздушный
поток
)
фаз
в
двухфазной
системе
.
Средняя плотность двухфазного потока
записывается
в
виде
:
(
)
возч
ρβρβρ
⋅−+⋅=
1 , (8.17)
где
:
ρ
ч
и
ρ
воз
–
соответственно
,
плотности
дискретной
(
механические
примеси
)
и
сплошной
(
воз
-
душный
поток
)
фаз
в
двухфазной
системе
.
Формула
,
которая
связывает
объемную
и
расходную
концентрации
двухфазного
потока
,
имеет
вид
:
( )
ч
воз
ч
воз
ч
воз
ч
воз
v
v
v
v
x
x
⋅⋅
⋅−−
=
ρ
ρ
ρ
ρ
β
11
, (8.18)
где
: v
ч
и
v
воз
–
соответственно
,
действительные
средние
скорости
дискретной
(
механические
при
-
меси
)
и
сплошной
(
воздушный
поток
)
фаз
в
двухфазной
системе
.
Потери
давления
на
трение
двухфазного
потока
можно
определить
по
формуле
:
2
2
возвоз
дф
l
v
d
l
p
ρ
λ
=∆
, (8.19)
где
:
λ
дф
–
коэффициент
сопротивления
трения
двухфазного
потока
.
Коэффициент
сопротивления
трения
двухфазного
потока
превышает
коэффициент
сопротивле
-
ния
трения
однофазного
воздушного
потока
.
В
случае
незначительных
концентраций
и
малых
размеров
твердых
частиц
двухфазный
поток
можно
рассматривать
как
однородную
среду
,
плотность
и
вязкость
которой
зависят
от
концентра
-
ции
твердых
частиц
.
Плотность
такой
среды
определяют
по
формуле
(8.17).
При
выполнении
практических
расчетов
потерь
давления
на
трение
в
системах
аспирации
и
пневмотранспорта
применяют
эмпирическую
формулу
:
(
)
xpp
воз
ll
⋅+∆=∆
α
1
, (8.20)
где
:
∆
p
l
и
∆
p
l воз
–
соответственно
,
потери
давления
запыленного
и
незапыленного
потоков
,
Па
.
α
–
эмпирический
коэффициент
,
который
зависит
от
вида
дискретного
материала
.
Потери
давления
в
местных
сопротивлениях
трубопроводов
с
двухфазными
потоками
опреде
-
ляют
по
выражению
(5.1).
Однако
при
этом
коэффициенты
местного
сопротивления
тройников
и
отводов
определяют
с
учетом
потерь
давления
на
«
разгон
»
механических
примесей
,
т
.
е
.
с
учетом
затрат
энергии
на
придание
ускорения
дискретных
частиц
.
Исходными
данными
для
расчета
внутренних
систем
аспирации
и
пневмотранспорта
являются
:
–
характеристика
и
количество
отходов
или
материалов
,
которые
транспортируются
;
–
расходы
воздушных
потоков
для
транспортирования
этих
отходов
(
материалов
);
–
выбранная
трасса
сети
воздуховодов
и
места
установки
вентиляторов
и
очистного
оборудова
-
ния
.
Характеристики
отходов
(
материалов
)
и
их
количество
принимают
в
соответствии
с
параметра
-
ми
работы
технологического
оборудования
,
а
расходы
воздуха
устанавливают
в
соответствии
с
паспортными
данными
на
оборудование
или
по
справочным
данным
.
Расходы
воздуха
должны
быть
достаточными
для
транспортирования
механических
примесей
,
т
.
е
.
транспортная
скорость
потока
v
тр
должна
превышать
критическую
скорость
v
кр
,
определяемую
по
выражению
(8.14).

АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
50
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
Для
предотвращения
забивания
вертикальных
участков
воздуховодов
механическими
примеся
-
ми
скорость
двухфазного
потока
должна
превышать
транспортную
скорость
на
величину
скорости
витания
частиц
примесей
,
т
.
е
.:
втрверт
vvv +=
,
где
: v
в
–
скорость
витания
частиц
,
м
/
с
.
Увеличение
скорости
потока
на
вертикальных
участках
воздуховодов
обеспечивается
путем
уменьшения
их
сечения
.
Переход
с
большего
сечения
на
меньшее
предусматривают
в
конце
гори
-
зонтального
участка
с
таким
расчетом
,
чтобы
после
перехода
до
отвода
оставался
участок
стаби
-
лизации
длиной
5÷6D,
где
D –
диаметр
воздуховода
.
Расчетную
массовую
расходную
концентрацию
двухфазного
потока
определяют
как
отношение
массового
расхода
механических
примесей
(
материалов
)
к
массовому
расходу
воздушного
потока
:
воз
ч
р
G
G
x =
.
Для
транспортирования
древесной
стружки
и
опилок
x
р
= 0,1÷0,6;
для
систем
пневмотранспорта
среднего
давления
x
р
= 0,7÷2,0;
для
систем
пневмотранспорта
высокого
давления
x
р
= 2,0÷5,0.
Потери
давления
в
воздуховодах
первоначально
рассчитывают
для
потоков
незапыленного
воз
-
духа
.
При
этом
особое
внимание
уделяется
увязыванию
потерь
давления
в
ответвлениях
от
маги
-
страли
(
допускается
невязка
до
5%).
Конусные
диафрагмы
допускается
устанавливать
на
верти
-
кальных
участках
воздуховодов
при
условии
,
что
механические
примеси
сухие
,
неволокнистые
и
нелипкие
.
Для
увеличения
потерь
давления
в
ответвлениях
можно
использовать
трубные
вставки
меньшего
диаметра
.
При
невозможности
использования
конусных
диафрагм
(
или
трубных
вста
-
вок
)
увеличивают
расчетный
расход
воздушного
потока
в
ответвлениях
.
Потери
давления
∆
p
для
выбора
нагнетателя
рекомендуется
принимать
с
учетом
потерь
давле
-
ния
в
магистрали
системы
∆
p
маг
,
в
устройствах
очистки
(
фильтры
,
циклоны
и
т
.
д
.)
∆
p
оч
,
а
также
высоты
подъема
h
транспортируемых
механических
примесей
(
материалов
)
и
10%
запаса
.
Напри
-
мер
,
для
систем
аспирации
и
пневмотранспорта
древесных
отходов
потери
давления
определяют
по
формуле
:
( )
оч
вч
воз
возррпмаг
p
vv
v
ghxxkpp ∆+
−
⋅⋅⋅⋅+⋅+∆⋅=∆
ρ
11,1
, (8.21)
где
:
∆
p
маг
–
потери
давления
незапыленного
потока
в
магистрали
системы
,
Па
.
k
п
–
коэффициент
,
принимаемый
для
межцеховых
систем
по
справочной
литературе
;
для
внутрицеховых
систем
пневмотранспорта
с
ответвлениями
к
технологическому
обору
-
дованию
k
п
= 1,4;
v
в
–
скорость
витания
,
м
/
с
;
v
ч
и
v
воз
–
соответственно
,
действительные
средние
скорости
дискретной
(
механические
при
-
меси
)
и
сплошной
(
воздушный
поток
)
фаз
в
двухфазной
системе
.
Для
других
систем
аспирации
и
пневмотранспорта
:
(
)
ррпмаг
ghxkpp
β
⋅⋅+⋅+∆⋅=∆ 11,1
, (8.22)
где
:
β
р
= W
ч
/W
воз
–
расчетная
объемная
концентрация
смеси
,
кг
/
м
3
.
