Лекции - Аэродинамика и вентиляция. Часть 1
Подождите немного. Документ загружается.


АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
11
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
минус
берется
потому
,
что
сила
трения
направлена
в
сторону
,
противоположную
направлению
по
-
тока
.
Работа
объемных
сил
будет
состоять
из
работы
по
перемещению
центра
тяжести
объема
на
уча
-
стке
1,1'
в
центр
тяжести
объема
на
участке
2,2'.
Обозначим
проекции
ускорения
,
вызванные
объемными
силами
на
оси
координат
,
через
X, Y
и
Z;
расстояние
между
центрами
тяжести
объемов
на
участках
1,1'
и
2,2' –
через
ds,
а
проекции
ds
на
оси
координат
–
через
dx, dy
и
dz.
В
таком
случае
работа
объемных
сил
составит
(
)
ZdzYdyXdxM ++∆
.
Изменение
энергии
сложится
,
очевидно
,
из
изменения
в
рассматриваемом
объеме
внутренней
и
кинетической
энергии
.
Изменение
внутренней
энергии
будет
равно
разности
внутренних
энергий
жидкости
на
участ
-
ках
1,1'
и
2,2'.
Обозначив
внутреннюю
энергию
объема
на
участке
1,1',
приходящуюся
на
единицу
массы
жидкости
через
U,
а
объема
на
участке
2,2' –
через
U+dU,
получим
,
что
искомое
изменение
внутренней
энергии
равно
∆
MdU.
Изменение
кинетической
энергии
будет
равно
разности
кинетических
энергий
жидкости
в
объ
-
емах
на
участках
1,1'
и
2,2'.
Обозначив
скорость
в
сечении
1-1
через
v,
а
в
сечении
2-2 –
через
v+dv,
получим
,
что
изменение
кинетической
энергии
без
учета
бесконечно
малых
величин
второго
порядка
составит
:
(
)
∆=
∆
−
+∆
222
22
2
v
dM
MvdvvM
.
Применяя
закон
сохранения
энергии
,
получим
:
( ) ( )
∆+∆=++∆+∆−∆−∆
2
2
v
MdMdUZdzYdyXdxMMdhgWpdMdq
.
Сокращая
на
∆
M =
ρ∆
W,
получим
уравнение
:
gdh
v
d
p
ddUZdzYdyXdxdq +
+
+=+++
2
2
ρ
. (2.1)
Из
термодинамики
известно
,
что
тепло
,
сообщенное
единице
массы
жидкости
,
расходуется
на
повышение
ее
внутренней
энергии
и
работу
по
расширению
ее
объема
:
+=
ρ
1
pddUdq
.
Вычитая
последнее
уравнение
из
уравнения
энергии
(2.1),
получим
обобщенное уравнение
Бернулли
:
gdh
v
d
dp
ZdzYdyXdx +
+=++
2
2
ρ
. (2.2)
Если
из
объемных
сил
действует
только
сила
тяжести
,
то
последнее
уравнение
упрощается
.
Выберем
прямоугольную
систему
координат
,
у
которой
оси
x
и
y
расположены
горизонтально
,
а
ось
z
направлена
навстречу
силе
тяжести
(
вверх
).
Тогда
проекции
ускорений
X = 0, Y = 0, Z = -g
и
уравнение
(2.2)
примет
вид
:
0
2
2
=+
++ dh
g
v
d
g
dp
dz
ρ
. (2.3)
Интегрируя
это
выражение
,
получаем
уравнение
Бернулли
:
consth
g
v
g
dp
z =+++
∫
2
2
ρ
. (2.4)
Входящий
в
последнее
выражение
интеграл
можно
взять
,
если
известно
,
как
изменяются
давле
-
ние
и
плотность
вдоль
рассматриваемой
струйки
.

АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
12
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
В
частном
случае
,
когда
ρ
= const,
интеграл
легко
берется
и
уравнение
Бернулли
для
жидкости
или
несжимаемого
газа
примет
вид
:
consth
g
v
g
p
z =+++
2
2
ρ
. (2.5)
Если
скорости
в
каждом
поперечном
сечении
струи
неодинаковы
,
то
,
разделив
струйку
на
эле
-
ментарные
струйки
и
применив
к
одной
из
них
уравнение
(2.5),
далее
выполнив
некоторые
мате
-
матические
преобразования
и
интегрирование
,
получим
:
consthdG
G
df
v
gGg
p
z
F
=+++
∫∫
1
2
1
3
ρ
ρ
.
Применяя
теорему
о
среднем
и
подставляя
G =
ρ
Fv
ср
,
можно
записать
:
(
)
consth
gv
v
g
p
z
ср
ср
ср
=+++
2
3
ρ
.
Заменим
здесь
среднюю
величину
куба
скорости
на
куб
средней
(
по
площади
)
скорости
:
(
)
33
срср
vv ⋅=
α
.
где
:
α
–
коэффициент Кориолиса
.
Теперь
окончательно
получим
следующее
уравнение
Бернулли
для
жидкости
или
несжимаемо
-
го
газа
:
consth
g
v
g
p
z
ср
ср
=+++
2
2
α
ρ
. (2.6)
Очень
часто
уравнение
Бернулли
используют
в
другой
форме
.
Запишем
уравнение
(2.6)
для
двух
сечений
и
умножим
все
его
члены
на
ρ
g:
p
v
pgz
v
pgz
срср
∆+++=++
2
2
2
2
222
1
2
111
ρ
αρ
ρ
αρ
. (2.7)
где
:
(
)
срср
hhghgp
12
∆−∆=∆=∆
ρρ
.
В
этом
уравнении
:
ρ
gz –
весовое
давление
; p –
статическое
давление
;
2
1
2
ср
v
ρ
α
–
динамиче
-
ское
(
скоростное
)
давление
.
Сумма
этих
трех
давлений
есть
полное
давление
,
а
∆
p –
потери
давле
-
ния
.
Коэффициент
Кориолиса
α
определяется
из
выражения
:
(
)
∫∫
===
1
0
3
3
3
333
3
11
fdv
k
dfv
Fvkv
v
F
осср
ср
α
,
где
ос
vvv /
=
и
Fdffd /
=
. (2.8)
Коэффициент
α
≥
1,
причем
α
= 1
при
равномерном
поле
скоростей
.
Коэффициенты
Кориолиса
α
и
Буссинеска
β
связаны
выражением
:
α
= 3
β
- 2. (2.9)
Уравнения
движения
(
Эйлера
,
Навье
-
Стокса
)
Из
механики
известно
,
что
если
на
какое
-
либо
тело
с
массой
∆
M
оказывает
воздействие
сила
R,
вызывающая
ускорение
тела
a,
то
справедливо
равенство
:
MaR
∆
=
.
Если
заменить
силу
и
ускорение
их
проекциями
на
оси
координат
,
то
это
равенство
можно
представить
в
виде
следующих
трех
равенств
:
zzyyxx
MaRMaRMaR ∆=∆=∆=
;;
. (2.10)
Применим
эти
равенства
для
описания
движения
потока
жидкости
.
АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
13
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
С
этой
целью
в
пространстве
с
движущейся
жидкостью
отметим
точку
А
,
в
которой
давление
равно
p,
а
проекции
скорости
v
x
, v
y
и
v
z
.
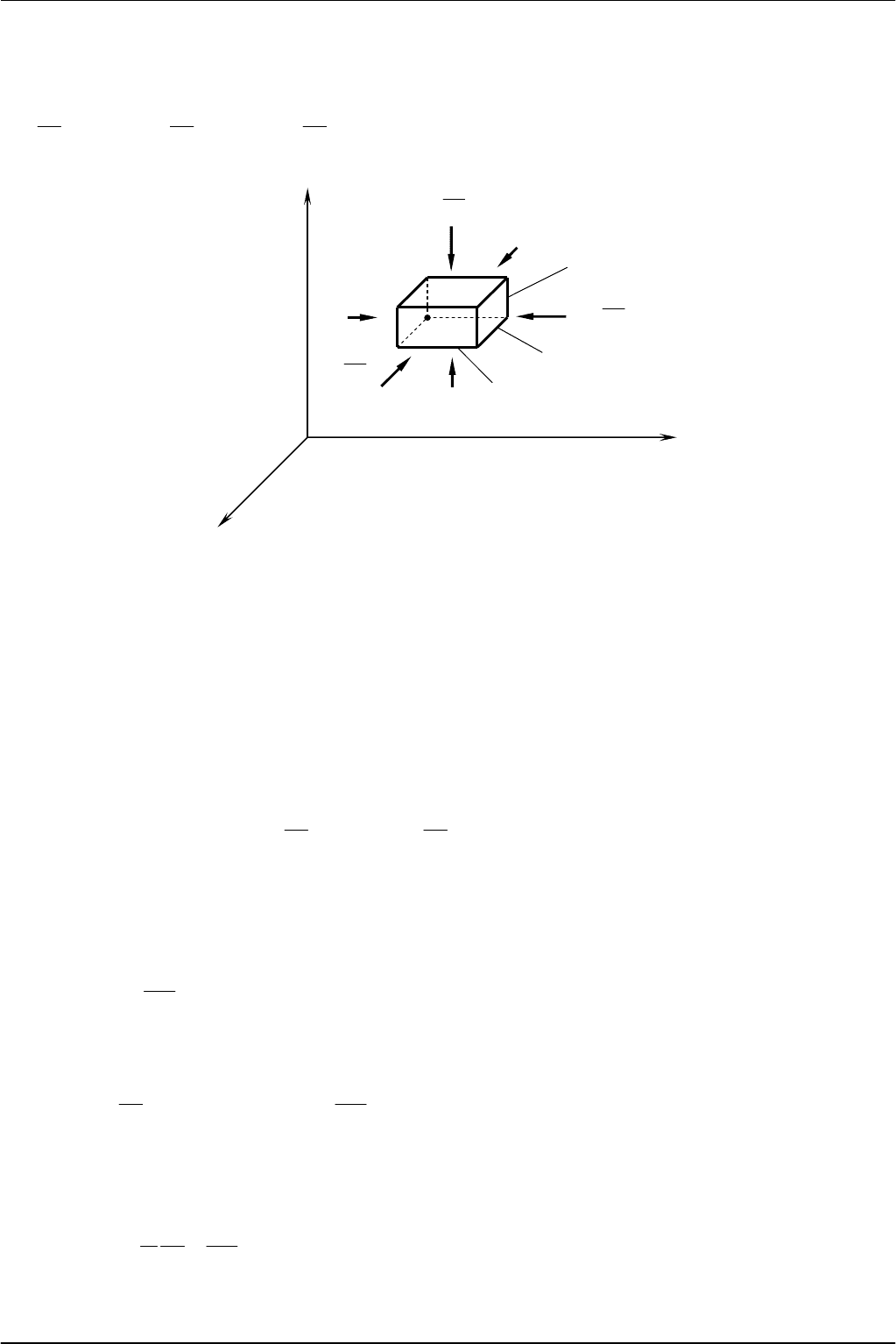
Выделим
около
точки
А
весьма
малый
параллелепипед
с
ребрами
∆
x,
∆
y,
∆
z (
рисунок
2.2).
На
его
противоположных
гранях
будут
следующие
давления
: p
и
x
x
p
p ∆
∂
∂
+
; p
и
y
y
p
p ∆
∂
∂
+
; p
и
z
z
p
p ∆
∂
∂
+
.
Рис
. 2.2 –
К
выводу
уравнения
движения
Примем
,
что
проекции
ускорения
массовых
сил
параллелепипеда
равны
X, Y
и
Z.
Рассмотрим
уравнение
,
составленное
из
проекций
величин
на
ось
абсцисс
.
Проекция
силы
R
x
равна
сумме
проекций
поверхностных
сил
R
x пов
и
объемных
сил
R
x об
:
об
x
пов
xx
RRR +=
.
Проекция
поверхностных
сил
слагается
из
нормальных
и
касательных
сил
.
В
целях
облегчения
вывода
уравнения
движения
касательные
силы
пока
не
будем
учитывать
.
Тогда
проекция
поверх
-
ностных
сил
будет
равна
разности
сил
,
действующих
на
противоположные
грани
параллелепипе
-
да
,
перпендикулярные
оси
x:
zyx
x
p
zyx
x
p
pzypR
повx
∆∆∆
∂
∂
−=∆∆
∆
∂
∂
+−∆∆=
.
Проекция
объемных
сил
будет
равна
:
MXR
обx
∆=
.
Проекцию
ускорения
a
x
можно
представить
в
виде
:
dt
dv
a
x
x
=
.
Поэтому
уравнение
,
составленное
из
проекций
величин
на
ось
абсцисс
,
запишется
следующим
образом
:
dt
dv
MMXzyx
x
p
x
∆=∆+∆∆∆
∂
∂
−
.
Разделим
все
члены
последнего
равенства
на
массу
параллелепипеда
zyxM
∆
∆
∆
=
∆
ρ
.
В
преде
-
ле
,
когда
размеры
параллелепипеда
∆
x,
∆
y,
∆
z
одновременно
стремятся
к
нулю
,
т
.
е
.
параллелепи
-
пед
стягивается
в
точку
А
,
получим
уравнение
движения
,
относящееся
только
к
точке
А
:
dt
dv
x
p
X
x
=
∂
∂
−
ρ
1
. (2.11)
А
p
p
z
z
p
p ∆
∂
∂
+
p
∆
y
∆
z
∆
x
x
y
z
x
x
p
p ∆
∂
∂
+
y
y
p
p ∆
∂
∂
+

АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
14
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
По
аналогии
можно
получить
два
других
уравнения
движения
,
содержащие
проекции
величин
на
другие
оси
координат
:
dt
dv
z
p
Z
dt
dv
y
p
Y
z
y
=
∂
∂
−=
∂
∂
−
ρρ
1
;
1
.
Входящие
в
уравнения
проекции
скорости
при
установившемся
движении
являются
только
функциями
координат
пространства
,
а
потому
справедливо
равенство
:
z
v
v
y
v
v
x
v
v
dt
dz
z
v
dt
dy
y
v
dt
dx
x
v
dt
dv
zyx
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
+
∂
∂
=
.
В
таком
случае
уравнения
движения
(
без
учета
сил
вязкости
)
окончательно
запишутся
так
:
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
−
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
−
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
−
.
1
;
1
;
1
z
v
v
y
v
v
x
v
v
z
p
Z
z
v
v
y
v
v
x
v
v
y
p
Y
z
v
v
y
v
v
x
v
v
x
p
X
z
z
z
y
z
x
y
z
y
y
y
x
x
z
x
y
x
x
ρ
ρ
ρ
(2.12)
Эти
три
уравнения
носят
название
уравнений движения Эйлера
.
В
уравнениях
отражена
связь
,
которая
существует
между
проекциями
ускорения
объемных
сил
,
плотностью
,
давлением
и
проекциями
скорости
в
какой
-
либо
точке
потока
.
При
учете
сил
вязкости
уравнения
движения
принимают
более
сложную
форму
.
Они
носят
на
-
звание
уравнений движения Навье-Стокса
:
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
−
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
−
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
−
.
1
;
1
;
1
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
z
v
v
y
v
v
x
v
v
z
v
y
v
x
v
z
p
Z
z
v
v
y
v
v
x
v
v
z
v
y
v
x
v
y
p
Y
z
v
v
y
v
v
x
v
v
z
v
y
v
x
v
x
p
X
z
z
z
y
z
x
zzz
y
z
y
y
y
x
yyy
x
z
x
y
x
x
xxx
ν
ρ
ν
ρ
ν
ρ
(2.13)
Уравнения
равновесия
несжимаемого
газа
в
состоянии
покоя
Рассмотрим
случай
,
когда
несжимаемый
газ
находится
в
состоянии
покоя
.
В
состоянии
покоя
(
т
.
е
.
при
отсутствии
движения
)
проекции
скорости
будут
равны
нулю
:
0===
zyx
uuu
.
В
соответствии
с
этим
условием
система
уравнений
движения
Эйлера
примет
вид
:
0
1
;0
1
;0
1
=
∂
∂
−=
∂
∂
−=
∂
∂
−
z
p
Z
y
p
Y
x
p
X
ρρρ
. (2.14)
Эти
уравнения
носят
название
уравнений равновесия
,
поскольку
они
определяют
условия
со
-
стояния
покоя
.
Сориентируем
оси
координат
в
пространстве
таким
образом
,
чтобы
положительное
направле
-
ние
оси
z
было
направлено
навстречу
силе
тяжести
.
В
этом
случае
проекции
ускорения
массовых
сил
будут
равны
:
gZYX
−
=
=
=
;0;0
.
Вследствие
этого
уравнения
равновесия
примут
вид
:
g
z
p
y
p
x
p
ρ
−=
∂
∂
=
∂
∂
=
∂
∂
;0;0
.
АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
15
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
Умножая
первое
уравнение
на
dx,
второе
–
на
dy,
третье
–
на
dz
и
почленно
складывая
левые
и
правые
части
полученных
уравнений
,
получим
:
dzgdp
⋅
⋅
−
=
ρ
.
Интегрируя
это
уравнение
(
при
условии
,
что
плотность
есть
величина
постоянная
),
получим
:
constCzgp
=
=
⋅
⋅
+
ρ
. (2.15)
Это
уравнение
выражает
основной закон аэростатики
.
Постоянную
интегрирования
С
можно
определить
из
граничных
условий
(
например
,
на
некото
-
ром
уровне
z = 0
давление
равно
p = p
0
).
В
этом
случае
C = p
0
,
и
поэтому
справедлива
формула
:
zgpp
⋅⋅−=
ρ
0
. (2.16)
Из
формулы
(2.16)
следует
,
что
давление
газа
(
например
,
воздуха
в
комнате
)
уменьшается
по
мере
увеличения
высоты
расположения
рассматриваемой
точки
относительно
исходного
уровня
.
Поверхностями уровня
называют
поверхности
,
в
каждой
точке
которой
давления
одинаковы
.
Для
таких
поверхностей
p = const, dp = 0.
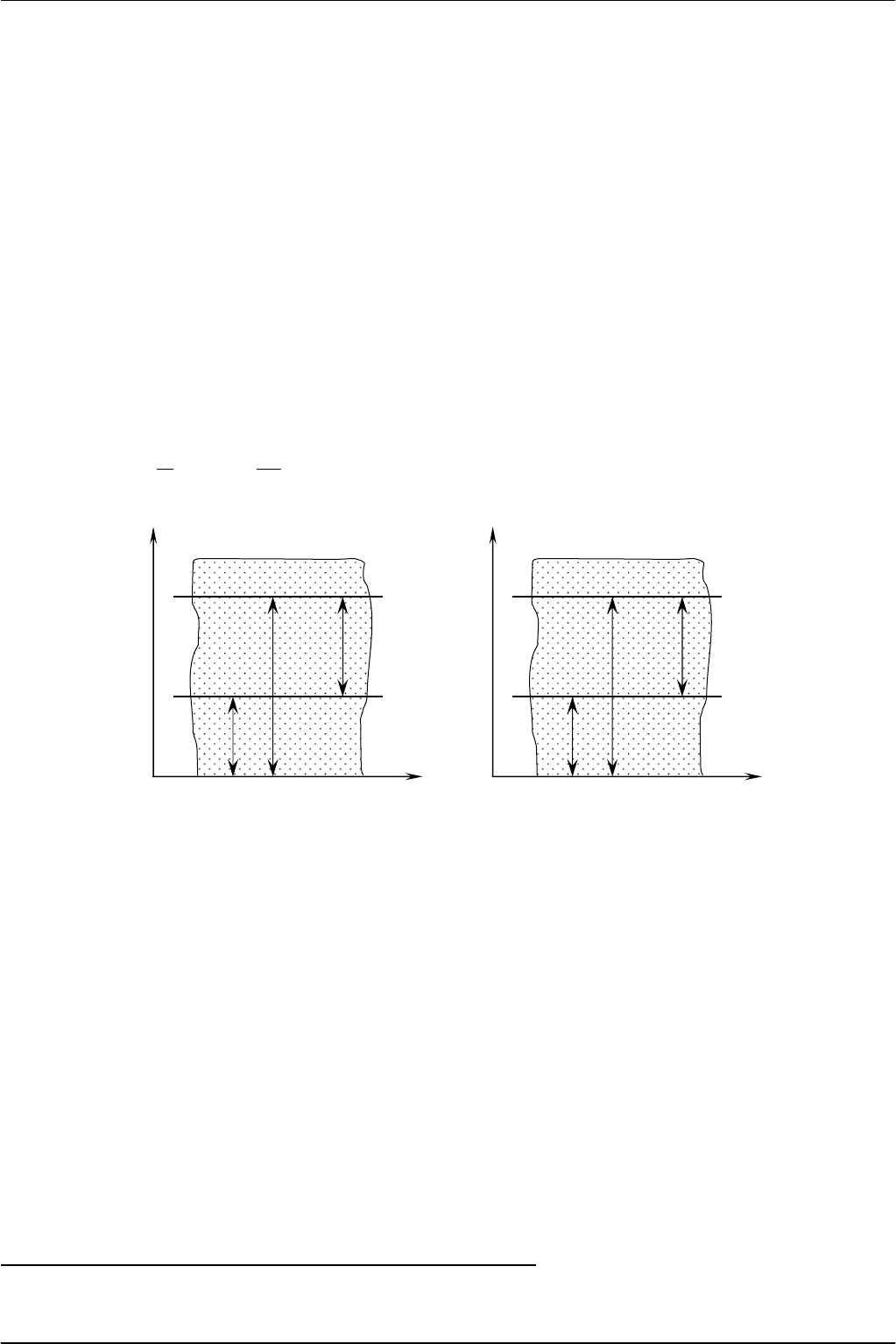
Если
выделить
в
воздушном
пространстве
две
поверхности
уровня
с
давлениями
p
и
p
0
и
верти
-
кальными
координатами
z
и
z
0
(
рисунок
2.3
а
),
то
можно
записать
:
ρρ
0
0
p
zg
p
zg +⋅=+⋅
,
откуда
(
)
hgpzzpp
⋅⋅+=−⋅+=
ρρ
000
(2.17)
Рис
. 2.3 –
К
выводу
основного
уравнения
аэростатики
Если
же
поверхности
уровня
поменять
местами
,
т
.
е
.
считать
,
что
заданная
поверхность
уровня
с
давлением
p
0
расположена
снизу
,
а
поверхность
с
давлением
p –
сверху
(
рисунок
2.3
б
),
то
полу
-
чим
:
(
)
(
)
hgpzzpzzpp
⋅⋅−=−⋅−=−⋅+=
ρρρ
00000
. (2.18)
Объединяя
формулы
(2.17)
и
(2.18),
получим
:
hgpp
⋅⋅±=
ρ
0
. (2.19)
Это
другая
форма
записи
основного
уравнения
аэростатики
,
удобная
для
практического
исполь
-
зования
.
Слагаемое
ρ
gh
в
уравнении
(2.19)
характеризует
вес
столба
несжимаемого
газа
высотой
h
и
площадью
в
1
квадратную
единицу
.
Знак
перед
вторым
слагаемым
в
правой
части
уравнения
зависит
от
расположения
искомой
точ
-
ки
с
давлением
p.
Если
эта
точка
находится
ниже
заданной
поверхности
с
давлением
p
0
,
то
в
урав
-
нении
(2.19)
следует
принимать
знак
«+»;
если
же
искомая
точка
расположена
выше
поверхности
с
давлением
p
0
,
то
следует
принимать
знак
«-».
Уравнения
равновесия
сжимаемого
газа
в
состоянии
покоя
Дифференциальное
уравнение
равновесия
газа
с
учетом
его
сжимаемости
(
ρ
≠
const)
можно
за
-
писать
в
виде
:
z
x
z
z
0
h
p
0
p
z
x
z
0
z
h
p
0
p
0
0
а
)
б
)
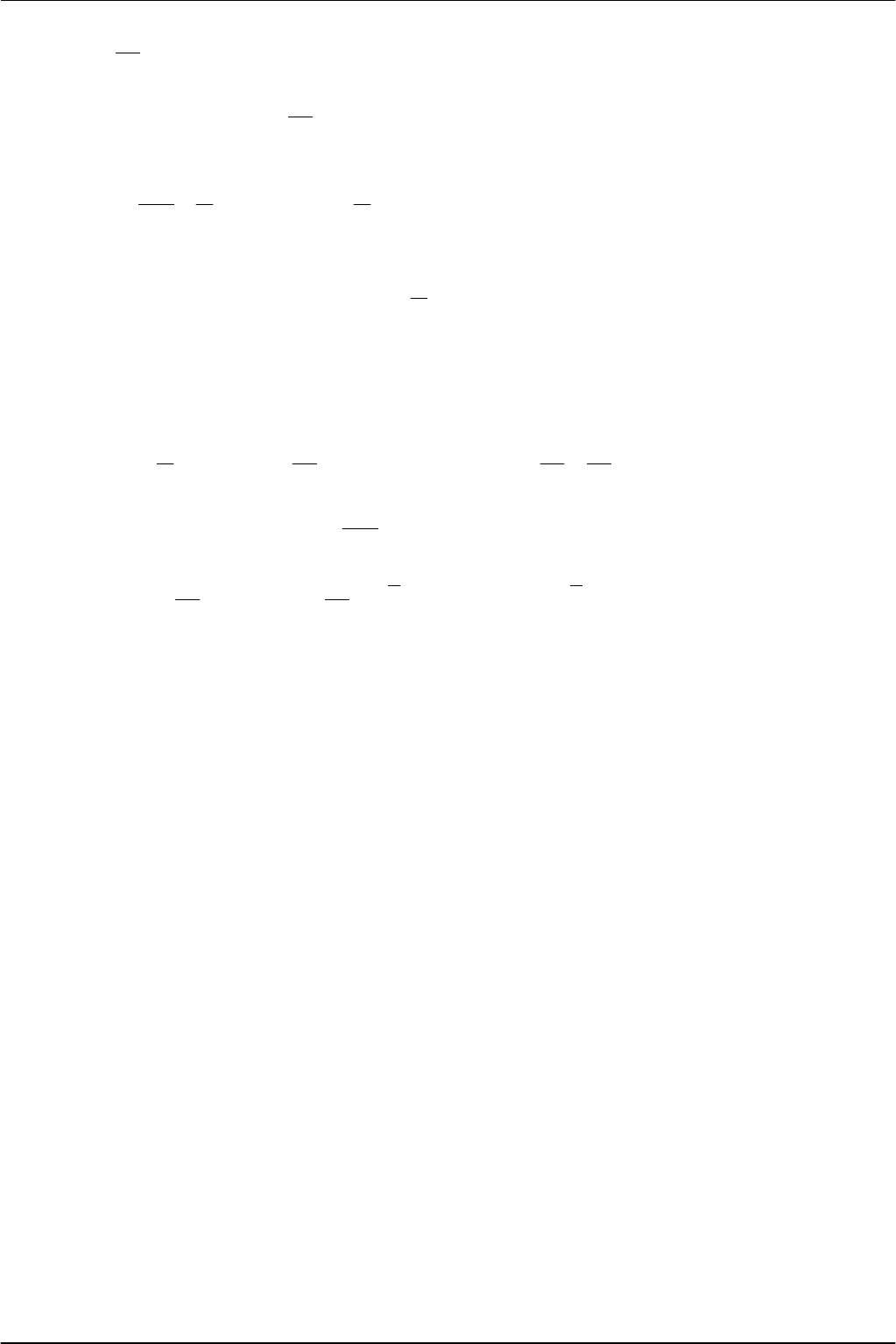
АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
16
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
constzg
dp
=⋅+
∫
ρ
. (2.20)
Для
вычисления
интеграла
∫
ρ
dp
необходимо
знать
закон
изменения
состояния
газа
.
Примем
,
что
температура
газа
постоянная
,
т
.
е
. T = const.
Тогда
,
учитывая
уравнение
Клапейрона
,
получим
:
C
p
TR
p
в
==
ρ
,
откуда
ρ
p
C =
,
где
:
С
–
постоянная
.
Подставляя
последнее
уравнение
в
выражение
(2.20)
и
выполняя
интегрирование
,
получим
:
constzgpC
=
⋅
+
⋅
lg
,
или
constp
p
zg =+⋅ lg
ρ
. (2.21)
Полученное
уравнение
отличается
от
основного
уравнения
аэростатики
тем
,
что
давление
газа
по
высоте
с
учетом
его
сжимаемости
в
изотермических
условиях
распределяется
не
по
линейному
,
а
по
логарифмическому
закону
.
Если
записать
уравнение
(2.21)
для
двух
высот
(z
и
z
0
),
и
,
учитывая
,
что
p/
ρ
= p
0
/
ρ
0
,
получим
:
0
0
0
0
lglg p
p
zgp
p
zg
ρρ
+⋅=+⋅
,
или
( )
p
pp
zzg
0
0
0
0
lg
ρ
=−⋅
.
Введя
обозначения
:
(
)
hzz
=−
0
и
H
g
p
=
0
0
ρ
,
получим
:
p
p
Hh
0
lg=
,
откуда
H
h
e
p
p
−
=
0
,
или
H
h
epp
−
=
0
. (2.22)
Если
сравнить
результаты
расчетов
,
выполненных
с
использованием
формул
(2.22)
и
(2.19),
т
.
е
.
с
учетом
и
без
учета
сжимаемости
газа
,
можно
прийти
к
следующим
выводам
.
Например
,
для
ат
-
мосферного
воздуха
,
при
изменении
высот
до
1200
м
,
его
можно
рассматривать
как
несжимаемый
газ
(
т
.
е
.
ρ
= const),
причем
погрешность
не
будет
превышать
1%.
Приблизительно
такой
же
резуль
-
тат
получается
и
при
использовании
другого
закона
изменения
газового
состояния
по
высоте
(
на
-
пример
,
адиабатического
).
Так
как
в
задачах
вентиляции
встречаются
значительно
меньшие
перепады
высот
,
погрешности
при
использовании
уравнений
аэростатики
будут
незначительные
,
что
и
оправдывает
их
широкое
использование
на
практике
для
рассмотрения
условий
равновесия
воздуха
.

АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
17
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
Лекция 3 – Основы кинематики потоков.
[1,
с
.25-34; 2,
с
.19-36]
Математическая
модель
движения
потока
(
Лагранж
,
Эйлер
)
Траектории
частиц
,
линии
тока
и
линии
отмеченных
частиц
Деформации
и
угловые
скорости
вращения
частиц
Вихревой
,
безвихревой
и
винтовой
потоки
Виды
простейших
потоков
Математическая
модель
движения
потока
(
Лагранж
,
Эйлер
)
Для
изучения
движения
воздушного
потока
необходимо
выбрать
соответствующую
математи
-
ческую
модель
.
Изучение
движения
воздушных
потоков
обычно
начинают
с
абстрактной
модели
невязкого
и
несжимаемого
потока
.
Как
и
в
механике
твердого
тела
,
сначала
изучаются
виды
движения
без
учета
действия
сил
,
ко
-
торые
вызывают
это
движение
(
кинематика
);
потом
рассматривается
движение
как
результат
дей
-
ствия
сил
(
динамика
).
В
соответствии
с
методом Лагранжа
рассматривается
поведение
частиц
потока
,
которые
пере
-
мещаются
в
пространстве
и
непрерывно
изменяют
свои
координаты
.
Для
начального
момента
времени
t
0
координаты
некоторой
произвольно
выбранной
частицы
(
относительно
неподвижной
системы
координат
)
будут
x
0
, y
0
, z
0
.
В
произвольный
момент
времени
t
координаты
этой
точки
бу
-
дут
определяться
в
соответствии
с
зависимостями
:
(
)
( )
( )
=
=
=
.;;;
;;;;
;;;;
0003
0002
0001
tzyxz
tzyxy
tzyxx
ϕ
ϕ
ϕ
(3.1)
Проекции
скорости
движения
этой
частицы
на
оси
координат
определятся
следующим
образом
:
(
)
( )
( )
==
==
==
.
;;;
;
;;;
;
;;;
0003
0002
0001
dt
tzyxd
dt
dz
u
dt
tzyxd
dt
dy
u
dt
tzyxd
dt
dx
u
z
y
x
ϕ
ϕ
ϕ
(3.2)
Т
.
е
.
в
соответствии
с
методом
Лагранжа
необходимо
знать
начальное
местоположение
(
началь
-
ные
координаты
)
и
закон
движения
каждой
частицы
.
Так
как
в
потоке
частиц
бесконечное
множе
-
ство
,
то
использование
этого
метода
весьма
затруднительно
.
При
использовании
метода Эйлера
изучают
,
что
происходит
с
потоком
в
заданных
точках
про
-
странства
в
определенные
моменты
времени
.
Представим
пространство
,
заполненное
воздушным
потоком
.
Через
некоторую
точку
этого
по
-
тока
с
координатами
x, y, z
с
течением
времени
будут
проходить
частицы
с
той
или
иной
скоро
-
стью
,
которая
характеризуется
вектором
u
r
и
его
проекциями
на
оси
координат
u
x
, u
y
, u
z
.
Таким
образом
,
вектор
местной
скорости
является
функцией
положения
точки
и
времени
:
(
)
trfu ,
r
r
=
,
где
:
r
r
–
радиус
-
вектор
рассматриваемой
точки
,
выражается
через
единичные
векторы
(
орты
)
по
осям
координат
в
соответствии
с
формулой
:
kzjyixr
⋅
+
⋅
+
⋅
=
r
, (3.3)
Составляющие
мгновенной
скорости
потока
в
данной
точке
можно
записать
в
виде
:
(
)
( )
( )
=
=
=
.;;;
;;;;
;;;;
3
2
1
tzyxfu
tzyxfu
tzyxfu
z
y
x
(3.4)

АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
18
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
Обычно
для
изучения
движения
потока
используется
метод
Эйлера
.
В
дальнейшем
в
данном
курсе
для
исследования
движения
воздушных
потоков
будет
использоваться
именно
этот
метод
.
Если
поле
скоростей
потока
не
изменяется
с
течением
времени
,
то
движение
потока
называют
установившимся
(
стационарным
).
В
этом
случае
характеристики
движения
изменяются
только
при
переходе
от
одной
точки
к
другой
(
при
изменении
координат
).
Тогда
функциональная
зависи
-
мость
для
местной
скорости
потока
будет
определяться
из
выражения
:
(
)
rfu
r
r
=
,
А
составляющие
мгновенной
скорости
потока
в
данной
точке
:
(
)
( )
( )
=
=
=
.;;
;;;
;;;
3
2
1
zyxfu
zyxfu
zyxfu
z
y
x
(3.5)
Установившееся
движение
может
быть
равномерным
и
неравномерным
.
При
равномерном
движении
скорости
в
подобных
точках
постоянные
и
не
зависят
от
координат
этих
точек
.
Примером
такого
движения
может
служить
воздушный
поток
при
постоянном
расходе
в
трубопроводе
постоянного
сечения
.
При
неравномерном
движении
скорости
в
подобных
точках
не
меняются
во
времени
,
но
явля
-
ются
функциями
координат
этих
точек
.
В
качестве
примера
такого
движения
может
быть
исполь
-
зован
воздушный
поток
в
трубопроводе
переменного
сечения
.
В
зависимости
от
площади
сечения
скорость
движения
вдоль
трубопровода
будет
изменяться
,
но
в
определенных
сечениях
она
будет
оставаться
постоянной
независимо
от
времени
.
В
общем
случае
,
когда
характеристики
поля
скоростей
потока
меняются
с
течением
времени
и
справедливы
зависимости
(3.3)
и
(3.4),
движение
называют
неустановившимся
(
нестационар-
ным
).
Примерами
такого
движения
могут
служить
:
движение
потока
воздуха
в
трубопроводах
при
быстром
открывании
или
закрывании
запорной
арматуры
;
обтекание
зданий
при
порывистом
вет
-
ре
и
другие
.
Природа
неустановившегося
движения
очень
сложна
.
В
дальнейшем
будет
рассматриваться
только
установившееся
движение
воздушных
потоков
.
Траектории
частиц
,
линии
тока
и
линии
отмеченных
частиц
Для
геометрического
изображения
потока
можно
воспользоваться
понятием
траектории час-
тицы
.
Из
понятия
траектории
вытекает
,
что
она
фиксирует
изменение
положения
частицы
с
тече
-
нием
времени
.
Получим
уравнение
траектории
частицы
.
Если
частица
за
бесконечно
малый
промежуток
вре
-
мени
dt
переместилась
на
расстояние
dl,
то
ее
скорость
будет
равна
:
dt
dl
u =
.
Проекции
этой
скорости
на
оси
прямоугольной
системы
координат
будут
равны
:
dt
dz
u
dt
dy
u
dt
dx
u
zyx
=== ;;
,
где
: dx, dy, dz –
проекции
отрезка
dl
на
оси
координат
.
Предыдущие
выражения
можно
записать
в
другом
виде
:
dt
u
dz
dt
u
dy
dt
u
dx
zyx
=== ;;
,
Так
как
левые
части
последних
выражений
равны
одной
и
той
же
величине
,
то
их
можно
при
-
равнять
друг
другу
.
Выполнив
это
,
получим
дифференциальное уравнение траектории части-
цы
:

АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
19
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
zyx
u
dz
u
dy
u
dx
==
. (3.6)
В
некоторых
случаях
удобнее
пользоваться
понятием
линии
тока
.
Представим
себе
поле
скоро
-
стей
в
потоке
,
которое
соответствует
некоторому
моменту
времени
t.
Выделим
произвольную
точку
А
1
(
рисунок
3.1),
в
которой
скорость
равна
u
1
.
вблизи
точки
А
1
на
направлении
вектора
скорости
u
1
выделим
точку
А
2
,
в
которой
скорость
равна
u
2
.
Вблизи
точки
А
2
на
направлении
вектора
скорости
u
2
выделим
точку
А
3
,
в
которой
скорость
равна
u
3
.
Продолжим
подобные
построения
для
точек
А
4
,
А
5
и
т
.
д
.
соединив
полученные
точки
последовательно
отрез
-
ками
прямых
,
получим
ломаную
линию
.
Если
все
сегменты
этой
ломаной
линии
одновременно
уменьшить
до
бесконечно
малых
вели
-
чин
,
то
получим
кривую
,
в
каждой
точке
которой
вектор
скорости
будет
направлен
по
касатель
-
ной
.
Эту
кривую
линию
и
называют
линией тока
.
Если
движение
неустановившееся
,
то
в
заданной
точке
потока
направление
скорости
изменяет
-
ся
во
времени
(
рисунок
3.2).
Т
.
е
.,
с
течением
времени
изменяется
положение
в
пространстве
линий
тока
,
которые
проходят
через
данную
точку
.
В
момент
времени
t
1
через
заданную
точку
проходила
линия
тока
1,
а
в
момент
времени
t
2
–
линия
тока
2.
Через
каждую
точку
потока
можно
провести
только
одну
линию
тока
,
другими
словами
,
линии
тока
не
пересекаются
(
если
предположить
противное
–
две
линии
тока
пересекаются
,
то
получим
,
что
в
один
и
тот
же
момент
времени
в
одной
точке
скорость
имеет
два
различных
направления
,
что
,
естественно
,
невозможно
).
Совокупность
линий
тока
дает
картину
движения
потока
в
данный
момент
времени
,
другими
словами
,
фотоснимок
направлений
местных
скоростей
потока
.
Основное
отличие
траекторий
частиц
от
линий
тока
состоит
в
следующем
.
Траектория
фикси
-
рует
изменение
положения
частицы
в
пространстве
с
течением
времени
,
а
линия
тока
для
фикси
-
рованного
момента
времени
определяет
направления
скоростей
в
различных
точках
пространства
потока
.
Следует
отметить
,
что
для
установившегося
движения
потока
траектории
частиц
и
линии
тока
совпадают
.
Наряду
с
понятиями
траектории
и
линии
тока
в
аэродинамике
пользуются
понятием
линии
от
-
меченных
частиц
.
Это
линия
,
на
которой
находятся
все
частицы
,
которые
прошли
через
одну
ка
-
кую
-
то
точку
пространства
.
Линию
отмеченных
частиц
можно
получить
,
если
в
воздушный
поток
поместить
тонкую
трубку
и
вводить
через
нее
дым
или
какой
-
либо
другой
краситель
.
Окрашенные
частицы
будут
подхватываться
потоком
и
двигаться
вместе
с
ним
.
Таким
образом
будет
визуально
формироваться
линия отмеченных частиц
(
или
линия окрашенных частиц
).
В
случае
установившегося
движения
потока
линия
отмеченных
частиц
совпадает
с
траекторией
и
линией
тока
.
Деформации
и
угловые
скорости
вращения
частиц
На
самостоятельную
проработку
[1,
с
.27-31; 2,
с
.27-31]
А
1
А
2
А
3
А
4
А
5
u
1
u
2
u
3
u
4
u
5
Рис
. 3.1
Рис
. 3.2
u
1
u
2
1
1
2
2
t
1
t
2
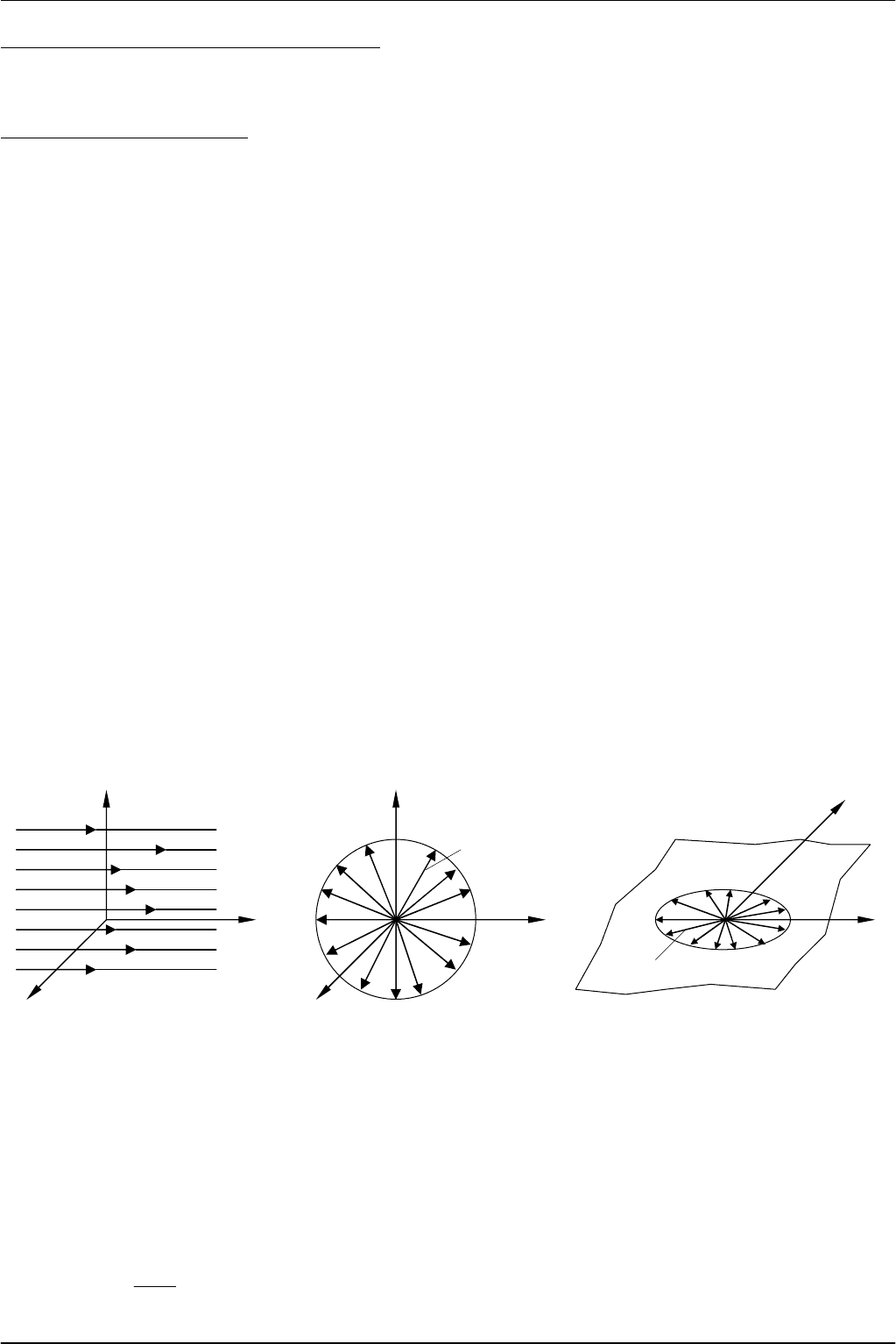
АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
20
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
Вихревой
,
безвихревой
и
винтовой
потоки
На
самостоятельную
проработку
[2,
с
.31-33].
Виды
простейших
потоков
Однородный поступательный поток
.
Имеется
безграничный
поток
,
все
частицы
которого
движутся
прямолинейно
и
параллельно
друг
другу
(
рисунок
3.3).
Определим
скорость
как
функ
-
цию
координат
точки
.
Ориентировав
оси
координат
таким
образом
,
чтобы
направление
положительной
оси
абсцисс
совпало
с
направлением
движения
,
получим
проекции
скорости
:
0;0; ===
zyx
vvconstv
.
Проекция
скорости
на
ось
абсцисс
постоянна
,
так
как
если
бы
она
была
переменна
,
то
,
согласно
уравнению
расхода
,
траектории
частиц
не
были
бы
параллельны
.
Поэтому
:
const
v
=
. (3.7)
Следовательно
,
скорость
не
зависит
от
координат
точки
.
Заметим
,
что
в
таком
потоке
не
будет
деформации
и
вращения
частиц
.
Действительно
,
любая
производная
от
постоянной
скорости
будет
равна
нулю
,
поэтому
скорости
деформации
и
вращения
частиц
также
будут
равны
нулю
.
Пространственный источник-точка
.
Данный
объект
является
абстракцией
,
в
реальности
не
существующей
,
и
,
чтобы
уяснить
его
смысл
,
представим
следующее
.
Жидкость
или
газ
нагнетается
по
очень
тонкой
трубке
в
пустотелый
шарик
.
На
поверхности
шарика
равномерно
расположено
много
мелких
отверстий
.
Через
эти
отверстия
жидкость
или
газ
вытекает
из
шарика
и
распространяется
во
все
стороны
равномерно
и
прямолинейно
.
Объемный
расход
равен
L.
Если
допустить
,
что
трубка
становится
бесконечно
тонкой
,
радиус
шарика
бесконечно
малым
,
а
число
отверстий
бесконечно
большим
,
то
в
пределе
получим
пространственное
истечение
жидко
-
сти
или
газа
из
точки
.
Такое
нереальное
течение
называется
пространственным течением из ис-
точника-точки
(
рисунок
3.4).
В
аэродинамике
при
решении
различных
задач
(
в
том
числе
и
практического
характера
)
реаль
-
ные
течения
заменяют
течением
из
совокупности
таких
источников
-
точек
.
Определим
,
как
изменяется
скорость
с
удалением
от
источника
-
точки
.
Источник
-
точку
помес
-
тим
в
начало
прямоугольных
координат
,
опишем
сферу
радиусом
r (
с
центром
в
начале
коорди
-
нат
).
По
условию
задачи
все
частицы
,
расположенные
на
сфере
,
обладают
одинаковыми
скоростя
-
ми
,
направленными
перпендикулярно
поверхности
сферы
.
Применяя
уравнение
расхода
(1.11)
к
источнику
-
точке
и
сфере
,
получим
:
vrL
2
4
π
=
.
Отсюда
скорость
в
любой
точке
,
удаленной
от
начала
координат
на
расстояние
r,
равна
:
2
4
r
L
v
π
=
. (3.8)
x
y
z
x
y
z
r
x
y
r
Рис
. 3.3
Рис
. 3.4
Рис
. 3.5
