Лекции - Аэродинамика и вентиляция. Часть 1
Подождите немного. Документ загружается.


АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
21
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
Таким
образом
,
скорость
обратно
пропорциональна
квадрату
расстояния
любой
точки
от
про
-
странственного
источника
-
точки
.
Определим
проекции
скорости
на
оси
координат
.
С
этой
целью
воспользуемся
равенствами
:
zzyyxx
vvvvvv
θθθ
cos;cos;cos ⋅=⋅=⋅=
,
где
:
θ
x
,
θ
y
,
θ
z
–
углы
между
вектором
скорости
v
и
осями
координат
.
r
z
r
y
r
x
zyx
===
θθθ
cos;cos;cos
,
222
zyxr ++=
.
Отсюда
проекции
скорости
на
оси
координат
будут
равны
:
( ) ( ) ( )
2/3
222
2/3
222
2/3
222
4
;
4
;
4
zyx
zL
v
zyx
yL
v
zyx
xL
v
zyx
++
=
++
=
++
=
πππ
.
В
потоке
от
источника
-
точки
деформация
имеется
,
а
вращения
частиц
не
происходит
.
Плоский источник-точка
.
Жидкость
или
газ
нагнетается
в
бесконечно
длинную
тонкую
труб
-
ку
.
По
всей
боковой
поверхности
равномерно
расположено
много
мелких
отверстий
.
Через
эти
от
-
верстия
жидкость
или
газ
вытекает
из
трубки
и
распространяется
равномерно
и
прямолинейно
во
все
стороны
.
Если
предположить
,
что
трубка
стала
бесконечно
тонкой
,
а
число
отверстий
в
трубке
стало
бес
-
конечно
большим
,
то
в
пределе
получим
пространственное
истечение
из
прямой
линии
.
Причем
течение
в
любой
плоскости
,
перпендикулярной
этой
прямой
,
будет
одинаковым
.
Такие
течения
в
аэродинамике
получили
название
плоских течений
.
Рассмотрим
течение
в
одной
какой
-
либо
плоскости
.
Это
течение
называется
плоским
течением
из
источника
-
точки
(
рисунок
3.5).
Выясним
,
как
изменяется
скорость
с
удалением
частицы
жидкости
или
газа
от
плоского
источ
-
ника
-
точки
.
Проведем
вокруг
него
окружность
радиуса
r.
По
условию
задачи
все
частицы
,
распо
-
ложенные
на
окружности
,
обладают
одинаковыми
скоростями
,
направленными
перпендикулярно
окружности
.
Применяя
уравнение
расхода
(1.11)
к
источнику
-
точке
и
окружности
,
получим
:
rvL
π
2
=
.
где
: L –
расход
в
плоском
источнике
-
точке
.
Скорость
в
любой
точке
,
удаленной
от
плоского
источника
-
точки
на
расстояние
r,
равна
:
r
L
v
π
2
=
. (3.9)
Таким
образом
,
скорость
обратно
пропорциональна
расстоянию
любой
точки
от
плоского
ис
-
точника
-
точки
.
Определим
проекции
скорости
на
оси
координат
.
Оси
системы
координат
ориентируем
так
,
чтобы
ось
z
совпала
с
осью
плоского
источника
-
точки
.
Тогда
:
yyxx
vvvv
θθ
cos;cos ⋅=⋅=
,
где
:
θ
x
,
θ
y
–
углы
между
вектором
скорости
v
и
осями
координат
.
r
y
r
x
yx
==
θθ
cos;cos
,
22
yxr +=
.
Отсюда
проекции
скорости
на
оси
координат
будут
равны
:
2222
2
;
2 yx
yL
v
yx
xL
v
yx
+
=
+
=
ππ
.
В
потоке
от
плоского
источника
-
точки
деформация
имеется
,
а
вращения
частиц
не
происходит
.
АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
22
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
Лекция 4 – Движение воздушного потока в трубопроводах.
[1,
с
.66-91; 2,
с
.114-140]
Потери
энергии
во
время
движения
воздушного
потока
Особенности
движения
воздушного
потока
в
трубопроводах
Потери
давления
в
воздуховоде
постоянного
сечения
Коэффициент
сопротивления
трения
Потери
энергии
во
время
движения
воздушного
потока
Получение
конкретных
зависимостей
для
расчета
потерь
энергии
во
время
движения
воздушно
-
го
потока
в
трубопроводах
является
основным
содержанием
задачи
аэродинамики
.
Сначала
рассмотрим
самый
простой
,
но
,
вместе
с
тем
,
самый
распространенный
случай
движе
-
ния
–
равномерное движение
.
Основной
задачей
при
изучении
равномерного
движения
воздуш
-
ного
потока
является
определение
потерь
энергии
(
которые
идут
на
преодоление
сопротивлений
)
на
единицу
длины
трубопровода
.
Равномерным
называют
установившееся
движение
воздушного
потока
,
при
котором
скорость
каждой
элементарной
струйки
потока
не
изменяется
по
длине
трубопровода
.
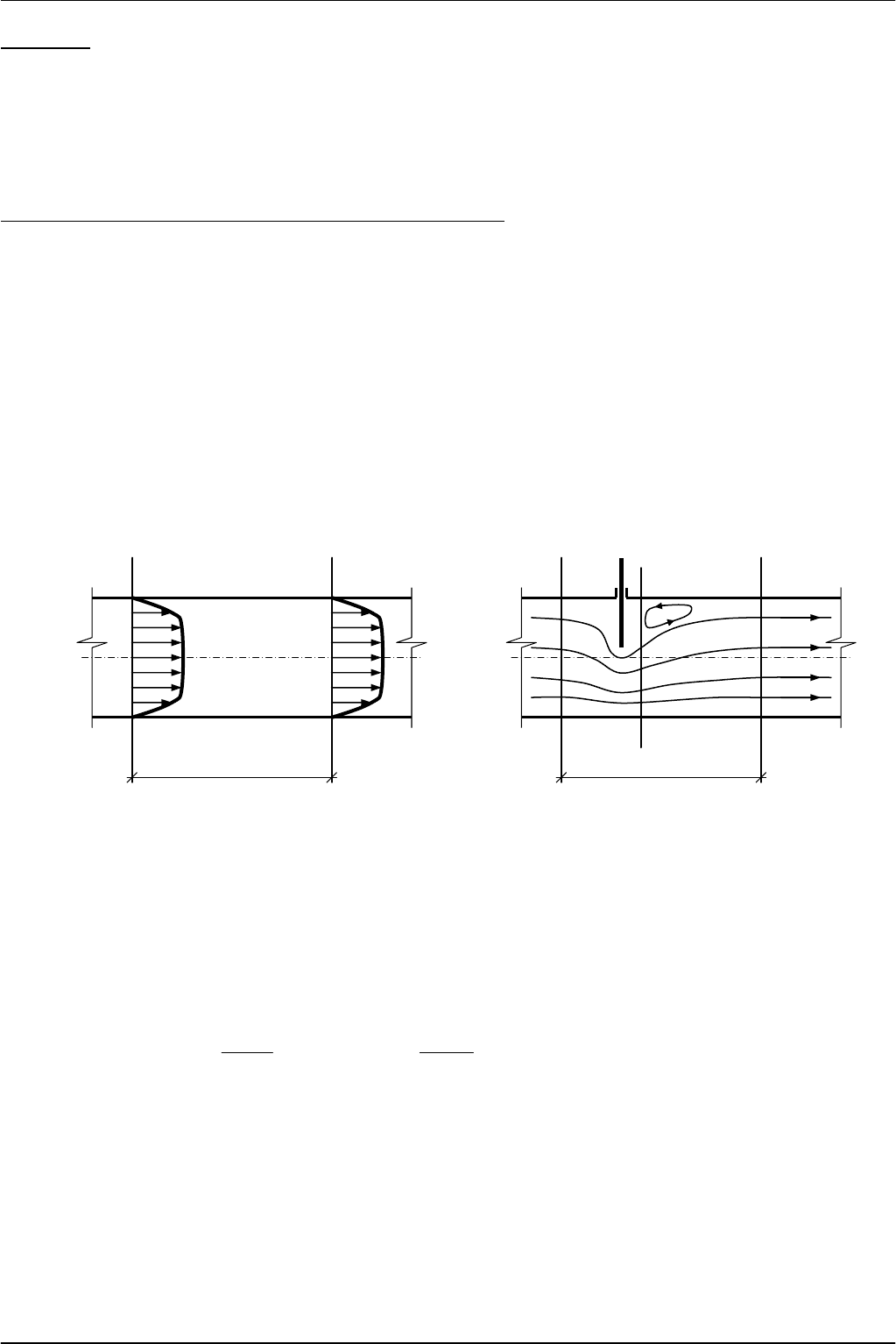
При
равномерном
движении
потока
его
живое
сечение
,
значения
и
распределение
скоростей
остаются
постоянными
.
Равномерное
движение
может
наблюдаться
в
цилиндрических
и
прямоугольных
трубопроводах
достаточной
длины
при
условии
,
что
поток
во
время
движения
остается
несжимаемым
(
рисунок
4.1
а
).
Неравномерным
называют
движение
воздушного
потока
,
в
котором
скорости
элементарных
струек
изменяются
(
либо
по
длине
изменяется
живое
сечение
потока
,
либо
при
постоянном
живом
сечении
изменяется
распределение
скоростей
,
либо
изменяется
и
то
и
другое
одновременно
).
Не
-
равномерное
движение
имеет
место
в
трубопроводах
переменного
сечения
,
при
обтекании
пото
-
ком
препятствий
на
его
пути
,
а
также
в
случаях
сжимаемого
потока
(
рисунок
4.1
б
).
Рассмотрим
равномерное
движение
воздушного
потока
в
горизонтальном
трубопроводе
круг
-
лого
сечения
(
рисунок
4.1
а
).
Запишем
уравнение
Бернулли
для
двух
сечений
потока
в
форме
дав
-
лений
:
p
v
pgz
v
pgz
срср
∆+++=++
2
2
2
2
222
1
2
111
ρ
αρ
ρ
αρ
.
Поскольку
в
рассматриваемом
случае
z
1
= z
2
, v
1ср
= v
2ср
и
α
1
=
α
2
,
то
ppp ∆=−
21
. (4.1)
Так
как
Еp
∆
=
∆
ρ
,
то
потеря
энергии
при
равномерном
движении
пропорциональна
разности
давлений
в
этих
сечениях
.
Если
допустить
,
что
потери
энергии
отсутствуют
(
∆Е
= 0),
то
р
1
=
р
2
.
Работа
сил
давления
расходуется
на
преодоление
сил
сопротивления
,
что
выражается
в
потерях
механической
энергии
.
Эти
потери
прямо
пропорциональны
длине
пути
движения
потока
и
их
на
-
зывают
удельными потерями энергии по длине
.
Если
потери
выражены
в
единицах
давления
,
то
их
называют
потерями давления по длине
и
обозначают
∆р
l
.
Если
потери
энергии
выражены
в
линейных
единицах
(
∆Е
/g),
их
называют
потерями напора по длине
и
обозначают
∆
h
l
.
1
1
2
2
l
1
1
2
2
l
С
С
а
)
б
)
Рис
. 4.1
АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
23
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
Различают
еще
местные потери давления
∆р
м
,
которые
возникают
вследствие
изменения
структуры
потока
в
локальных
элементах
трубопровода
(
соответственно
местные потери напора
∆
h
м
).
Особенности
движения
воздушного
потока
в
трубопроводах
Движение
воздуха
в
воздуховодах
может
быть
ламинарным
и
турбулентным
.
Ламинарное
течение
существует
в
воздуховодах
при
Re = vd/
ν
≤
2320,
где
v –
средняя
скорость
воздуха
в
воздуховоде
, d –
диаметр
воздуховода
.
Турбулентное
течение
наблюдается
при
значени
-
ях
Re > 2320.
Если
при
наличии
предварительно
успокоенного
воздуха
осторожно
увеличивать
скорость
,
то
можно
переход
ламинарного
течения
в
турбулентное
осуществить
даже
при
Re = 50000.
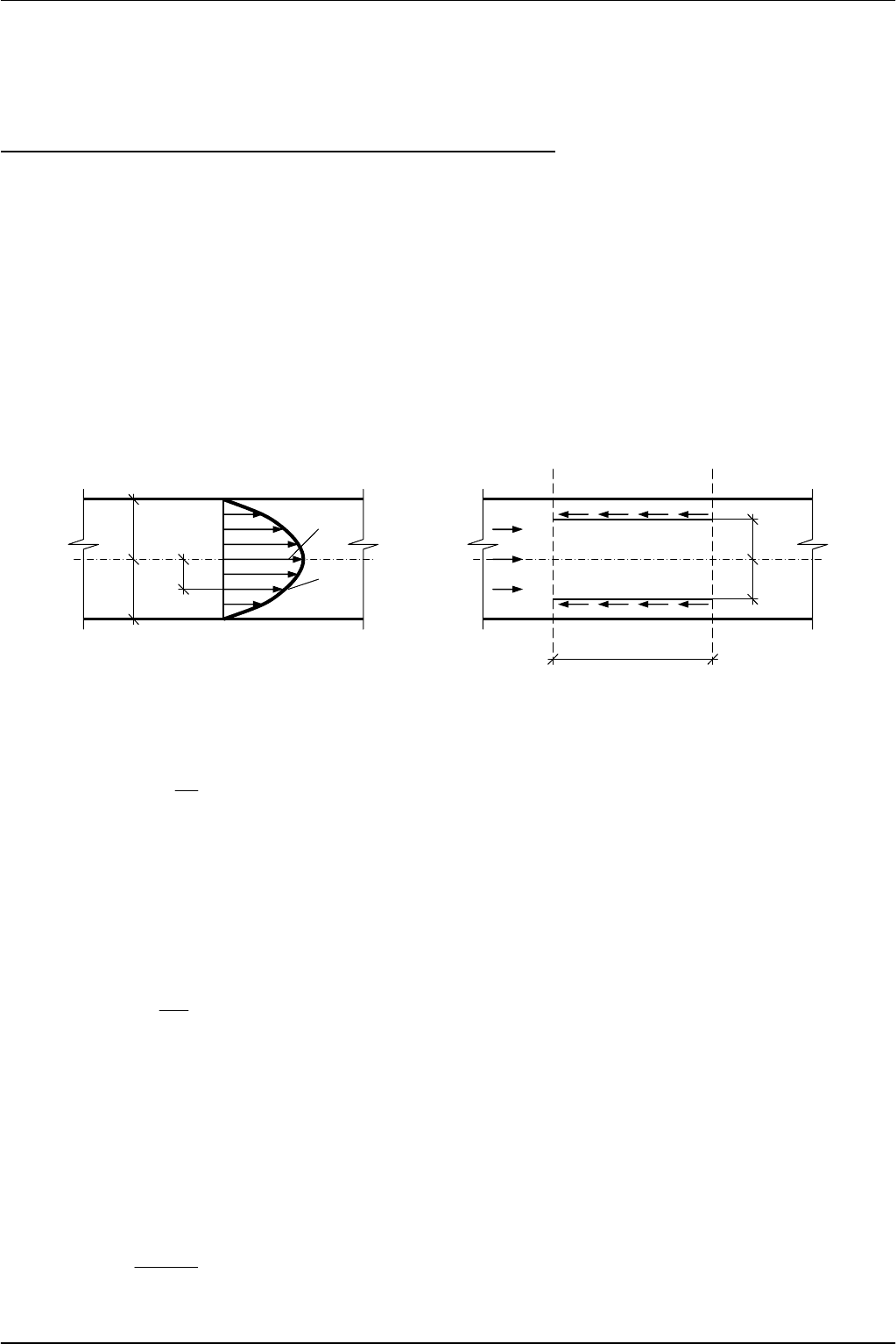
Установим
,
как
изменяется
скорость
в
поперечном
сечении
воздуховода
круглого
сечения
.
Вследствие
наличия
вязкости
,
скорость
движения
частиц
воздуха
в
непосредственной
близости
у
стенок
воздуховода
будет
практически
равна
нулю
(
воздух
как
бы
«
прилипает
»
к
стенкам
).
Эти
частицы
,
движущиеся
с
малой
скоростью
,
будут
подтормаживать
соседние
слои
воздуха
.
Поэтому
скорость
v
увеличивается
по
мере
удаления
от
поверхности
воздуховода
(
где
она
,
как
принято
считать
,
равна
нулю
)
и
достигает
наибольшей
величины
v
ос
на
оси
воздуховода
(
рисунок
4.2).
Выявим
зависимость
между
скоростями
v
и
v
ос
.
Вначале
рассмотрим
ламинарное
течение
.
Со
-
гласно
закону
Ньютона
,
касательное
напряжение
определяется
из
выражения
:
dr
dv
ρντ
−=
. (4.2)
где
: v –
скорость
воздуха
на
расстоянии
r
от
оси
воздуховода
.
Наличие
знака
«
минус
»
в
формуле
(4.2)
объясняется
тем
,
что
с
увеличением
радиуса
r
скорость
v
уменьшается
,
и
,
следовательно
,
градиент
dv/dr
отрицателен
,
а
величина
τ
всегда
положительна
.
Полная
производная
взята
вместо
частной
производной
потому
,
что
скорость
в
круглом
воздухо
-
воде
постоянного
сечения
обычно
изменяется
лишь
по
радиусу
трубы
.
Из
равенства
(4.2)
следует
:
drdv
τ
ρν
1
−=
. (4.3)
Для
определения
τ
проведем
в
воздуховоде
два
поперечных
сечения
1-1
и
2-2
на
расстоянии
l
одно
от
другого
.
Пусть
статическое
давление
в
сечении
1-1
равно
р
1
,
а
в
сечении
2-2 –
р
2
.
Выделим
в
объеме
между
сечениями
1-1
и
2-2
соосный
с
воздуховодом
цилиндр
радиусом
r (
рисунок
4.3).
Напишем
для
объема
этого
цилиндра
уравнение
количества
движения
в
проекциях
на
его
ось
,
полагая
,
что
количества
движения
,
проходящие
через
сечения
,
одинаковы
:
(
)
02
2
21
=⋅−−
rlrpp
πτπ
.
Из
этого
равенства
выразим
τ
:
r
l
pp
2
21
−
=
τ
. (4.4)
Подставляя
это
выражение
в
(4.3),
получим
:
R
R
r
v
v
ос
Рис
. 4.2
l
r
Рис
. 4.
3
r
τ
τ
1
1
2
2

АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
24
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
rdr
l
pp
dv
ρν
2
21
−
−=
.
Интегрирование
этого
уравнения
дает
:
c
r
l
pp
v +
−
−=
22
2
21
ρν
.
Постоянная
интегрирования
определяется
из
условия
,
что
на
стенке
трубы
(r = R)
скорость
рав
-
на
нулю
(v = 0).
Следовательно
:
22
2
21
R
l
pp
с
ρν
−
=
,
поэтому
−
−
=
2
2
2
21
1
4 R
r
R
l
pp
v
ρν
.
Зная
,
что
на
оси
воздуховода
(r = 0)
скорость
равна
осевой
(v = v
ос
),
находим
:
2
21
4
R
l
pp
v
ос
ρν
−
=
. (4.5)
Совместное
решение
двух
последних
уравнений
окончательно
дает
:
−=
2
2
1
R
r
vv
ос
. (4.6)
Как
видим
,
скорость
по
радиусу
воздуховода
круглого
сечения
при
ламинарном
течении
изме
-
няется
согласно
параболическому
закону
.
Рассмотрим
турбулентное
течение
.
Согласно
Прандтлю
,
касательное
напряжение
:
2
2
⋅=
dr
dv
l
п
ρτ
.
где
: l
п
–
длина
пути
перемешивания
.
Отсюда
:
dr
l
dv
п
2
⋅
=
ρ
τ
.
Подставляя
сюда
τ
из
выражения
(4.4),
получим
:
(
)
dr
ll
r
рр
dv
п
2
21
2 ⋅
−
=
ρ
.
Интегрирование
этого
уравнения
затруднено
из
-
за
того
,
что
длина
пути
перемешивания
являет
-
ся
неизвестной
функцией
.
Поэтому
до
сих
пор
для
турбулентного
течения
не
удалось
теоретиче
-
ски
точно
решить
задачу
об
изменении
скорости
по
радиусу
сечения
круглого
воздуховода
.
Вслед
-
ствие
этого
обычно
используются
экспериментальные
данные
.
Опытами
было
установлено
,
что
при
турбулентном
течении
:
n
ос
R
r
vv
/1
1
−=
. (4.7)
Показатель
степени
1/n
по
данным
опытов
уменьшается
с
увеличением
турбулизации
потока
.
Анализ
зависимости
(4.7)
показывает
,
что
с
увеличением
степени
турбулизации
потока
(
т
.
е
.
с
рос
-
том
величины
Re),
распределение
скоростей
по
сечению
воздуховода
делается
более
равномерным
и
при
1/n
→
0
имеем
v = v
ос
.
Обычно
в
расчетах
принимают
n = 7,
тогда
зависимость
(4.7)
именуют
законом
1/7
степени
.
Потери
давления
в
воздуховоде
постоянного
сечения
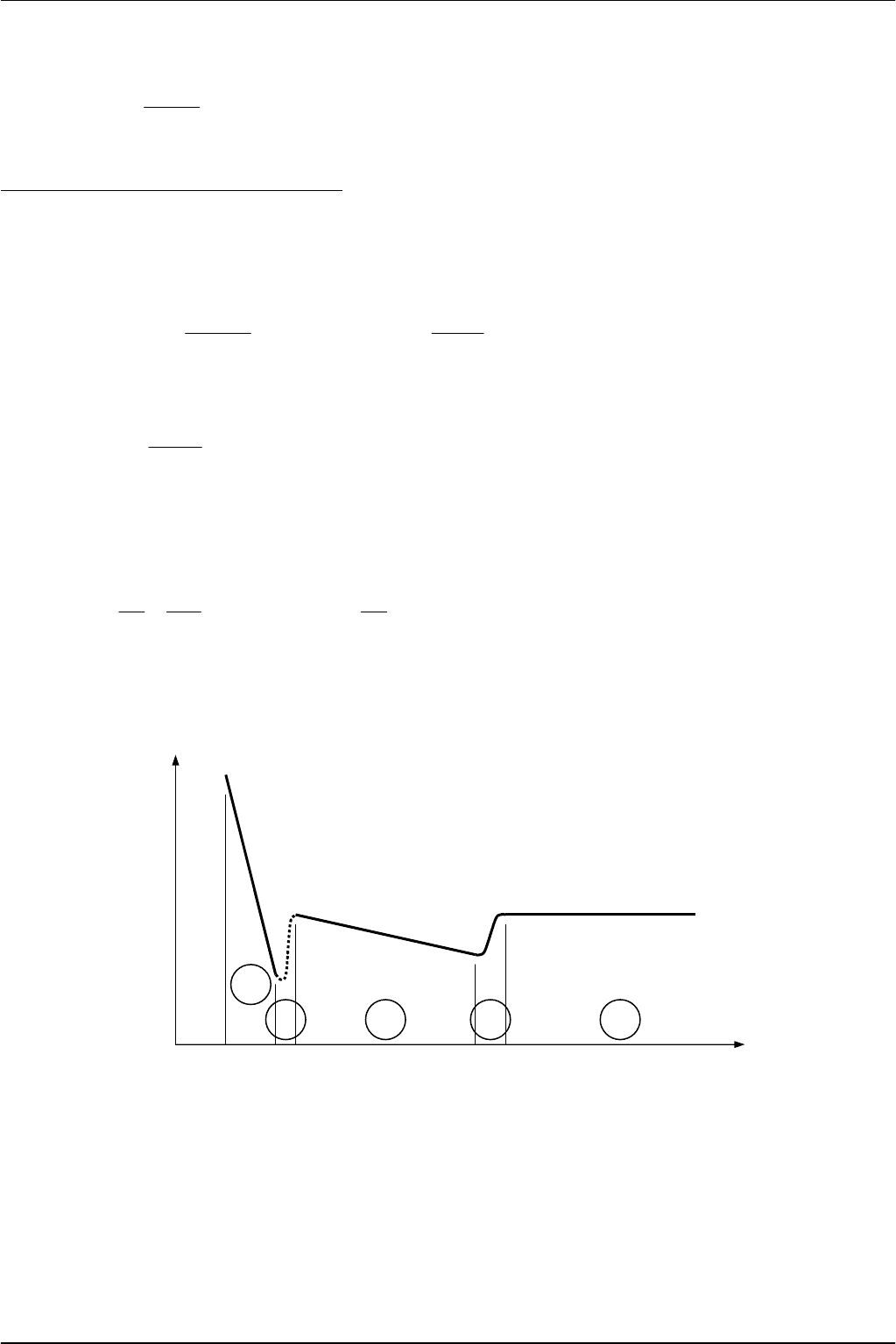
Определим
потери
давления
на
трение
в
воздуховоде
постоянного
сечения
(
рисунок
4.4).
Про
-
ведя
в
нем
два
поперечных
сечения
1-1
и
2-2,
напишем
уравнение
Бернулли
,
полагая
,
что
в
обоих

АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
25
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
сечениях
динамические
давления
одинаковы
.
Тогда
:
ppp ∆+=
21
,
откуда
21
ppp −=∆
. (4.8)
Рассмотрим
вначале
воздуховод
круглого
сечения
.
Выделив
объем
воздуха
,
заключенный
меж
-
ду
сечениями
1-1
и
2-2,
напишем
уравнение
количества
движения
в
проекциях
на
ось
воздуховода
:
( )
0
4
0
2
21
=⋅−− dl
d
pp
πτ
π
.
где
: d –
диаметр
воздуховода
;
l –
расстояние
между
сечениями
1-1
и
2-2;
τ
0
–
касательное
напряжение
на
стенке
воздуховода
.
Из
последнего
уравнения
следует
:
d
l
pp
021
4
τ
=−
.
Откуда
,
учитывая
(4.8),
получим
:
d
l
p
0
4
τ
=∆
. (4.9)
На
основании
опытов
было
замечено
,
что
касательное
напряжение
на
стенке
воздуховода
про
-
порционально
динамическому
давлению
,
вычисленному
по
средней
скорости
:
2
2
0
ср
v
ρ
ψτ
=
. (4.10)
где
:
ψ
–
коэффициент
пропорциональности
.
Подставив
выражение
(4.10)
в
(4.9),
получим
:
2
4
2
ср
v
d
l
p
ρ
ψ
=∆
.
Вводя
обозначение
4
ψ
=
λ
,
окончательно
получим
:
2
2
ср
v
d
l
p
ρ
λ
=∆
. (4.11)
где
:
λ
–
коэффициент сопротивления трения
.
Рассмотрим
теперь
воздуховод
произвольного
поперечного
сечения
,
причем
F –
площадь
,
а
P –
периметр
поперечного
сечения
.
Выполнив
аналогичные
выкладки
(
как
для
воздуховода
круглого
сечения
),
получим
:
2
4
2
ср
v
F
Pl
p
ρ
λ
=∆
. (4.12)
Если
ввести
обозначение
4F/P = d
э
,
получим
формулу
для
определения
потерь
давления
на
тре
-
ние
в
воздуховоде
произвольного
сечения
:
2
2
ср
э
v
d
l
p
ρ
λ
=∆
. (4.13)
где
: d
э
–
эквивалентный диаметр
.
l
Рис
. 4.
4
τ
0
1
1
2
2
v
p
2
F
p
1
F
АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
26
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
Если
,
например
,
воздуховод
прямоугольного
сечения
,
то
F = ab, P = 2(a + b),
где
a
и
b –
длины
сторон
прямоугольного
сечения
.
В
этом
случае
эквивалентный
диаметр
равен
:
( )
ba
ab
d
э
+
=
2
. (4.14)
Коэффициент
сопротивления
трения
В
случае
ламинарного
течения
коэффициент
сопротивления
трения
достаточно
просто
можно
установить
теоретически
.
Потери
давления
на
трение
определяются
по
формуле
(4.8).
Разность
статических
давлений
может
быть
найдена
из
зависимости
для
осевой
скорости
в
круглом
воздуховоде
(4.5).
Тогда
:
2
21
4
R
lv
pp
ос
ρν
=−
.
или
ос
v
d
l
pp
2
21
16
ρν
=−
.
Известно
,
что
коэффициент
поля
скоростей
k
при
ламинарном
течении
равен
0,5,
т
.
е
v
ос
= 2v
ср
.
С
учетом
этого
получим
:
ср
v
d
l
p
2
32
ρν
=∆
. (4.15)
Таким
образом
,
потери
давления
на
трение
при
ламинарном
течении
прямо
пропорциональны
скорости
движения
∆р
~ v
ср
.
Приравнивая
потери
на
трение
по
формулам
(4.11)
и
(4.15),
и
производя
сокращение
общих
множителей
в
левой
и
правой
частях
равенства
,
получим
:
d
v
ср
ν
λ
32
2
=
,
откуда
Re
64
=
λ
. (4.16)
Полученная
формула
хорошо
подтверждается
опытными
данными
.
Если
для
какого
-
либо
воздуховода
с
постоянной
шероховатостью
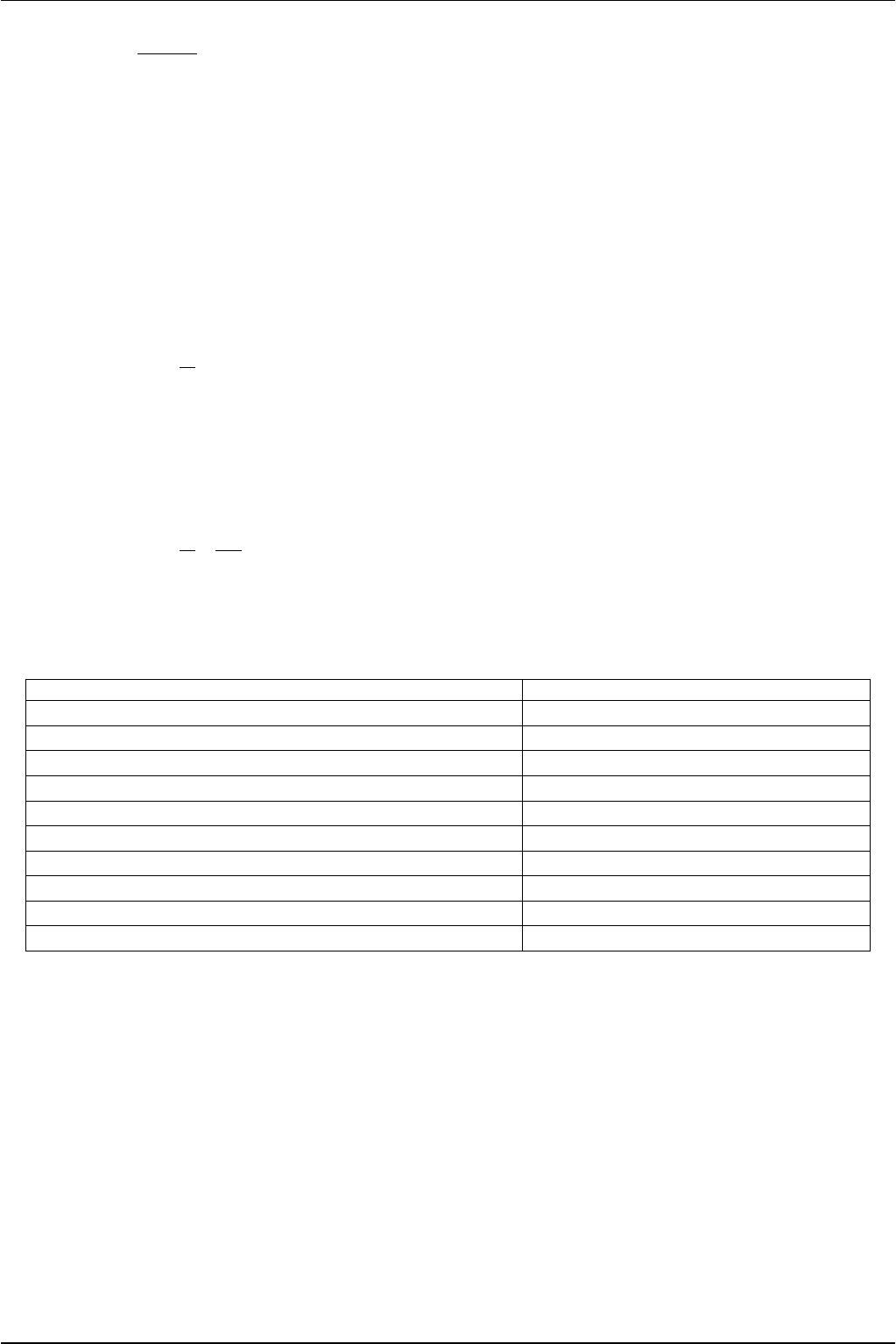
стенок
построить
зависи
-
мость
коэффициента
трения
λ
от
числа
Re (
при
постоянных
значениях
диаметра
d
и
коэффициента
кинематической
вязкости
ν
),
она
будет
выглядеть
примерно
так
,
как
это
показано
на
рисунке
4.5.
В
условиях
ламинарного
течения
(
рисунок
4.5,
участок
1)
коэффициент
трения
уменьшается
при
увеличении
числа
Re.
Зависимость
выражается
формулой
(4.16).
При
достижении
потоком
критических
значений
числа
Re (Re
кр
= 2000…4000)
режим
движения
скачкообразно
переходит
из
ламинарного
режима
в
турбулентный
(
рисунок
4.5,
участок
2).
В
случае
турбулентного
режима
течения
при
невысоких
значениях
чисел
Re,
пограничный
слой
покрывает
выступы
шероховатостей
стенок
воздуховода
.
Это
соответствует
течению
в
так
назы
-
ваемых
гидравлически
гладких
трубопроводах
(
рисунок
4.5,
участок
3).
Коэффициент
трения
для
гидравлически
гладких
труб
вычисляется
в
соответствии
с
формулой
Блазиуса
:
λ
lg
Re
1
2
3
4 5
Рис
. 4.5
АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
27
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
25,0
Re
3164,0
=
λ
. (4.17)
При
возрастании
числа
Re
толщина
пограничного
слоя
уменьшается
,
и
может
стать
меньше
вы
-
соты
выступов
шероховатостей
стенок
.
В
этот
момент
возможно
некоторое
возрастание
коэффи
-
циента
сопротивления
трения
(
рисунок
4.5,
участок
4).
Дальнейшее
увеличение
значений
числа
Re,
при
которых
толщина
пограничного
слоя
оказыва
-
ется
меньше
высоты
выступов
шероховатости
стенок
воздуховода
,
не
влияет
на
величину
коэф
-
фициента
сопротивления
трения
.
В
этом
случае
коэффициент
сопротивления
трения
зависит
толь
-
ко
от
шероховатости
стенок
(
так
называемый
автомодельный режим
течения
) –
участок
5
на
ри
-
сунке
4.5.
Коэффициент
сопротивления
трения
для
шероховатых
воздуховодов
можно
рассчитать
по
про
-
стой
формуле
Шифринсона
:
25,0
11,0
=
d
k
λ
. (4.18)
где
: k –
абсолютная шероховатость
стенки
воздуховода
,
м
.
Наибольшее
распространение
в
отечественной
практике
получила
формула
А
.
Д
.
Альтшуля
,
ко
-
торая
справедлива
как
для
гидравлически
гладких
,
так
и
для
шероховатых
воздуховодов
в
услови
-
ях
турбулентного
режима
течения
потока
:
25,0
Re
68
11,0
+=
d
k
λ
. (4.18)
Значения
абсолютной
шероховатости
k
для
трубопроводов
и
каналов
из
различных
материалов
приведены
в
таблице
4.1.
Таблица
4.1
Вид труб и каналов Абсолютная шероховатость стенок k, мм
Трубы
из
полиэтилена
и
поливинилхлорида
0,007
Трубы
асбестоцементные
0,05…0,1
Трубы
стальные
черные
(
новые
чистые
) 0,03…0,1
Трубы
стальные
оцинкованные
новые
0,1…0,2
Трубы
стальные
с
незначительной
коррозией
0,15…1,0
Трубы
стальные
корродированные
0,3…0,7
Трубы
стальные
старые
ржавые
1,0…3,0
Воздуховоды
стальные
на
фальцевых
соединениях
0,15
Трубы
чугунные
0,5…1,5
Трубы
из
цветных
металлов
0,001

АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
28
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
Лекция 5 – Движение воздушного потока в трубопроводах.
[1,
с
.66-91; 2,
с
.114-140]
Общие
сведения
о
местных
сопротивлениях
Потери
давления
при
входе
в
воздуховод
постоянного
сечения
Потери
давления
при
расширении
поперечного
сечения
воздуховода
Потери
давления
при
сужении
поперечного
сечения
воздуховода
Потери
давления
в
местных
сопротивлениях
других
типов
Взаимное
влияние
местных
сопротивлений
Общие
сведения
о
местных
сопротивлениях
Местным
сопротивлением
называется
аэродинамическое
сопротивление
,
сосредоточенное
в
од
-
ном
месте
на
коротком
участке
воздуховода
.
Типичным
примером
местного
сопротивления
могут
служить
колено
,
тройник
,
решетка
,
дроссель
-
клапан
и
т
.
д
.
В
местных
сопротивлениях
всегда
происходит
перестройка
поля
скоростей
и
образование
на
границах
потоков
вихрей
.
Перестройка
поля
скоростей
и
поддержание
вращения
вихрей
требуют
затраты
энергии
.
Таким
образом
,
течение
воздуха
через
местные
сопротивления
всегда
сопровож
-
дается
потерями
давления
.
Теоретическим
определением
величины
потерь
давления
в
местных
сопротивлениях
занимают
-
ся
давно
.
Однако
число
аналитически
решенных
случаев
в
настоящее
время
невелико
.
Объясняет
-
ся
это
тем
,
что
до
сих
пор
не
разработан
общий
аналитический
метод
расчета
местных
сопротив
-
лений
.
Привлекаемые
же
для
решения
этой
задачи
основные
уравнения
аэродинамики
,
как
прави
-
ло
,
нуждаются
в
тех
или
иных
допущениях
.
В
результате
решение
получается
приближенным
.
Вследствие
этого
определение
потерь
давления
в
местных
сопротивлениях
главным
образом
пошло
по
экспериментальному
пути
.
Как
показывают
опыты
,
потери
давления
в
местных
сопро
-
тивлениях
обычно
пропорциональны
квадрату
скорости
.
Поэтому
для
определения
потерь
давле
-
ния
в
местных
сопротивлениях
принята
формула
(
формула Вейсбаха
):
2
2
v
p
ρ
ζ
=∆
. (5.1)
где
:
ζ
–
коэффициент местного сопротивления
.
Необходимо
отметить
,
что
коэффициент
ζ
при
турбулентном
движении
зависит
почти
исклю
-
чительно
от
геометрии
местного
сопротивления
.
Многочисленные
экспериментальные
исследования
подтверждают
,
что
условие
ζ
= const
для
данного
вида
местного
сопротивления
полностью
оправдывается
только
для
больших
значений
критерия
Re (Re > 2·10
4
…2·10
4
).
При
небольших
скоростях
потока
ζ
зависит
от
числа
Re (
при
ла
-
минарном
или
близком
к
нему
режиме
движения
потока
).
Определение
потерь
давления
в
местных
сопротивлениях
производится
всегда
при
условии
равномерного
поля
скоростей
на
входе
в
него
.
Практически
это
условие
выполняется
довольно
редко
.
Наоборот
,
почти
всегда
поле
скоростей
неравномерно
,
и
фактические
значения
коэффици
-
ентов
местных
сопротивлений
несколько
отличаются
от
расчетных
.
Однако
при
расчетах
воздухо
-
водов
этой
ошибкой
пренебрегают
.
Потери
давления
при
входе
в
воздуховод
постоянного
сечения
Воздух
засасывается
в
открытый
торец
воздуховода
.
При
входе
поток
сначала
сжимается
,
а
за
-
тем
расширяется
и
заполняет
все
поперечное
сечение
воздуховода
(
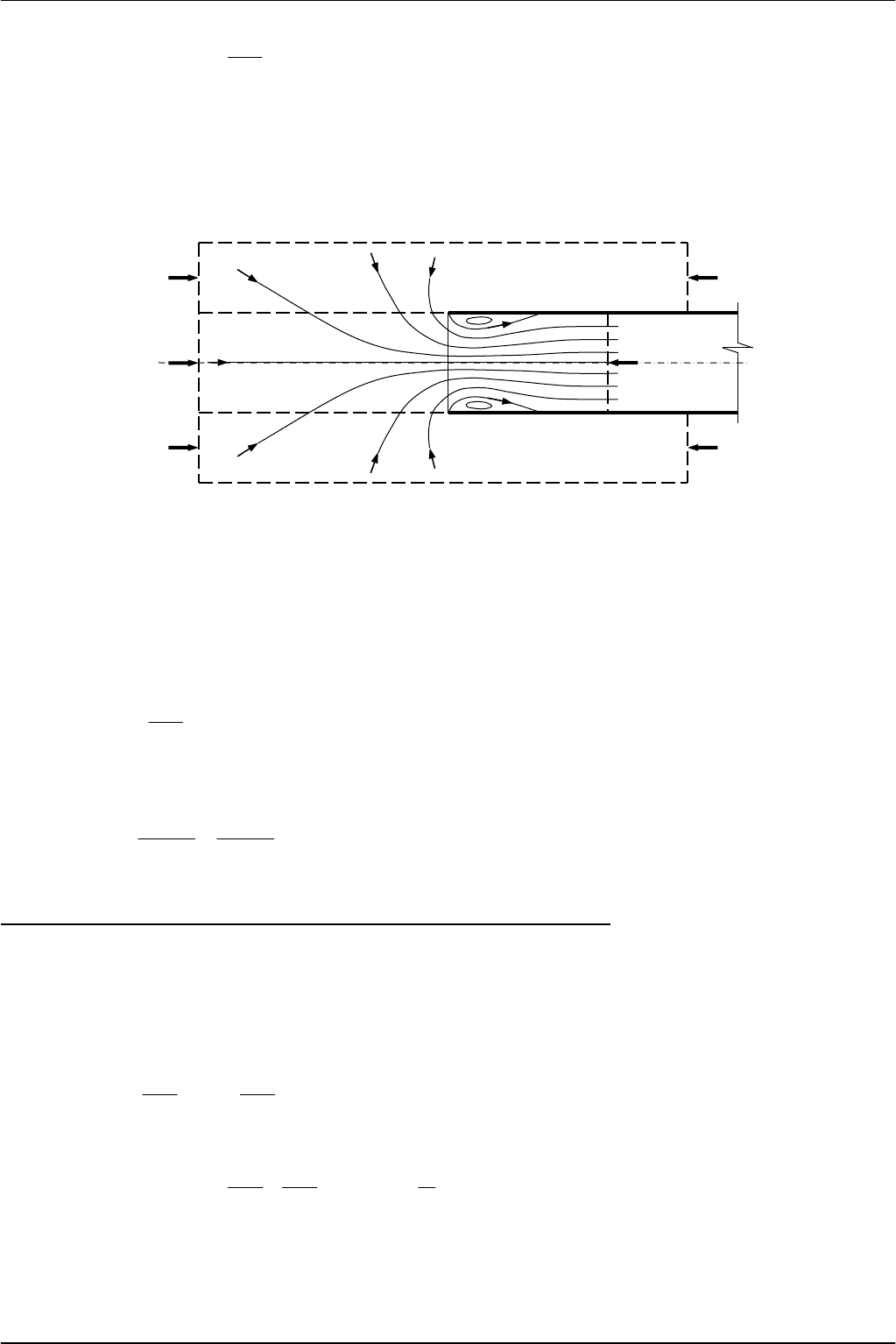
рисунок
5.1).
Выбрав
в
потоке
сечение
1-1
вдали
от
входа
,
на
таком
расстоянии
,
где
скоростью
можно
пре
-
небречь
,
и
сечение
2-2
в
том
месте
,
где
сжатый
поток
расширяется
,
и
поле
скоростей
становится
равномерным
,
напишем
уравнение
Бернулли
:
p
v
pp ∆++=
2
2
2
21
ρ
.
Отсюда
потери
давления
при
входе
в
воздуховод
составят
:
АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
29
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
2
2
2
21
v
ppp
ρ
−−=∆
. (5.2)
Разность
статических
давлений
может
быть
установлена
с
помощью
уравнения
количества
движения
.
С
этой
целью
проведем
вне
воздуховода
сечение
3-3
и
рассмотрим
объем
,
ограничен
-
ный
контуром
1-3-3-2-2-3-3-1.
Напишем
применительно
к
этому
объему
уравнение
количества
движения
в
проекциях
на
ось
воздуховода
:
2
221
FvFpFp
ρ
=−
.
При
составлении
этого
уравнения
полагаем
,
что
статические
давления
в
сечениях
1-1
и
3-3
весьма
близки
между
собой
,
а
скорости
на
границе
контура
вне
воздуховода
пренебрежимо
малы
.
Сокращая
последнее
уравнение
на
F,
получим
:
2
221
vpp
ρ
=−
.
Подставляя
эту
разность
статических
давлений
в
ранее
установленную
зависимость
для
потерь
давления
,
будем
иметь
:
2
2
2
v
p
ρ
=∆
. (5.3)
Итак
,
при
входе
воздуха
в
воздуховод
потеря
давления
равна
одному
скоростному
давлению
.
Тогда
коэффициент
местного
сопротивления
входа
:
1
2/
2/
2/
2
2
2
2
2
2
==
∆
=
v
v
v
p
ρ
ρ
ρ
ζ
. (5.4)
Потери
давления
при
расширении
поперечного
сечения
воздуховода
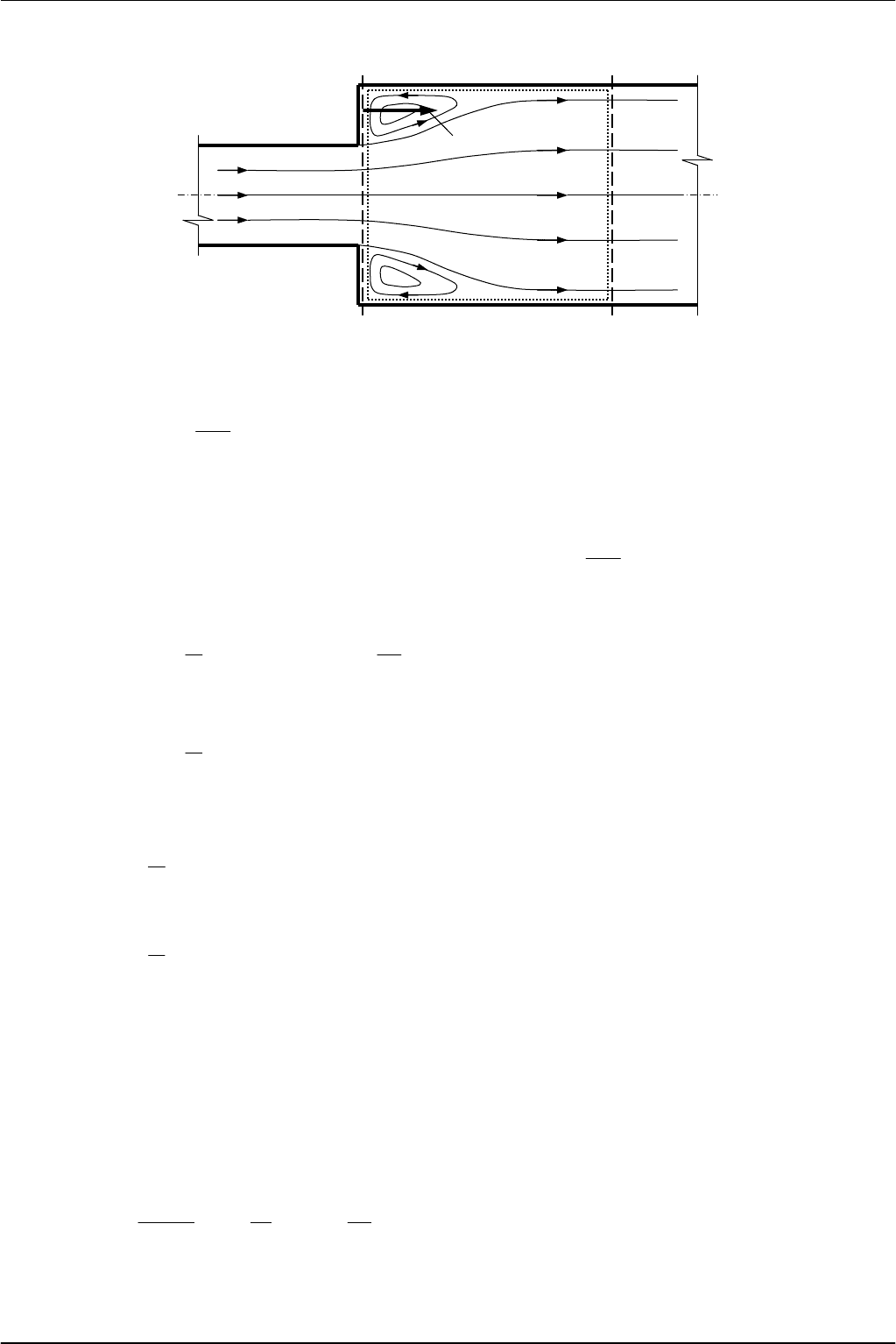
Представим
воздуховод
,
у
которого
по
направлению
течения
потока
происходит
внезапное
расширение
поперечного
сечения
(
рисунок
5.2).
Проведем
в
широкой
части
воздуховода
сечение
1-1,
а
на
достаточном
удалении
от
него
сече
-
ние
2-2,
где
поток
расширяется
и
заполняет
все
сечение
воздуховода
.
Для
выбранных
таким
образом
сечений
напишем
уравнение
Бернулли
:
p
v
p
v
p ∆++=+
2
2
2
2
2
2
1
1
ρρ
.
Отсюда
потери
давления
составят
:
( )
2
2
2
121
2
2
2
1
21
2
2
2
vvpp
vv
ppp −+−=−+−=∆
ρ
ρρ
. (5.5)
Выделим
объем
,
заключенный
между
обоими
сечениями
и
стенками
воздуховода
,
и
примени
-
тельно
к
нему
составим
уравнение
количества
движения
в
проекциях
на
ось
воздуховода
:
(
)
122
2
222212111
vvFvFFpFFrFp
ρρ
−=−−+
.
1
1
3
3
3
3
2
2
p
1
F
p
2
F
p
1
f
p
1
f
p
1
f
p
1
f
Рис
. 5.1
АЭРОДИНАМИКА ВЕНТИЛЯЦИИ. Конспект лекций. Часть 1.
30
ДонНАСА Кафедра ТТГВ. Маркин А.Н.
где
: r
1
–
среднее
реактивное
давление
торцовой
стенки
широкой
части
воздуховода
.
В
соответствии
с
равенством
(7.2) [1]
можем
написать
:
2
2
1
111
v
kpr
ρ
+=
.
где
: k
1
–
аэродинамический коэффициент
.
Подставляя
r
1
в
уравнение
количества
движения
,
получим
:
( ) ( )
2
2
1
121122
2
222212111
v
FFkvvFvFFpFFpFp
ρ
ρρ
−−−=−−+
.
Упрощая
это
выражение
и
сокращая
его
на
F
2
,
получим
:
−−−=−
2
1
2
1
112
2
221
122
2
v
F
F
kvvvpp
ρ
.
Согласно
уравнению
расхода
, F
1
/F
2
= v
2
/v
1
,
поэтому
:
( )
[
]
211112
2
221
22
2
vvvkvvvpp −−−=−
ρ
.
Подставим
эту
разность
статических
давлений
в
ранее
найденную
зависимость
для
потерь
дав
-
ления
.
Тогда
:
( ) ( )
[
]
2111
2
21
2
vvvkvvp −−−=∆
ρ
. (5.6)
Опытами
доказано
,
что
r
1
= p
1
.
В
таком
случае
k
1
= 0,
и
потому
:
( )
2
21
2
vvp −=∆
ρ
. (5.7)
Как
видим
,
потери
давления
при
внезапном
расширении
воздуховода
равны
скоростному
дав
-
лению
потерянной
скорости
.
Следует
отметить
,
что
явление
,
происходящее
при
внезапном
расширении
воздуховода
,
анало
-
гично
явлению
удара
в
механике
твердого
тела
.
Поэтому
потери
давления
при
внезапном
расши
-
рении
воздуховодов
очень
часто
называют
потерями
на
удар
,
а
выражение
(5.7)
носит
название
формула Борда
.
Коэффициент
местного
сопротивления
,
отнесенный
к
скорости
в
узкой
части
воздуховода
,
со
-
ставит
:
2
2
1
2
1
2
2
1
11
2/
−=
−=
∆
=
F
F
v
v
v
p
ρ
ζ
. (5.8)
1
1
2
2
Рис
. 5.2
r
1
(
F
2
-
F
1
)
