Lefebvre A.H., Ballal D.R. Gas Turbine Combustion: Alternative Fuels and Emissions

Подождите немного. Документ загружается.

60 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

Equations 2.35 and 2.36 provide simple dimensionless relationships

between the quenching distance and the fuel drop size in the spray.

Essentially, they state that quenching distance is directly proportional to

drop size and is inversely proportional to the square root of gas pressure.

An increase in ϕ and a reduction in ρ

both reduce d

because they promote

evaporation by increasing the surface area of the fuel. Similarly, an increase

in B also accelerates evaporation, thereby decreasing d

Values of E

min

may be obtained for quiescent or low-turbulence mixtures

by inserting the calculated values of d

from Equation 2.35 or Equation 2.36

into the expression

Ec Td

min

(

)

pA Astq

ρπ∆ 6

(2.37)

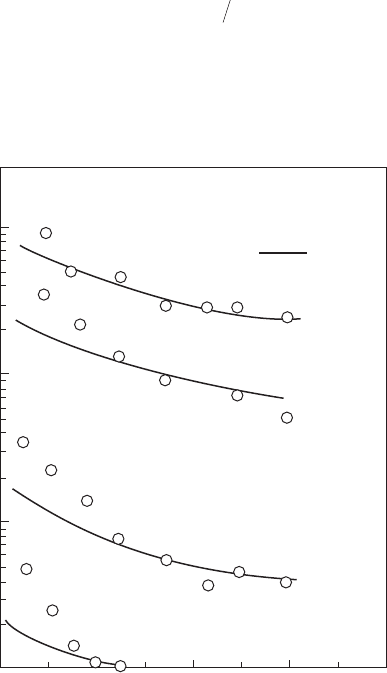
The results of such calculations are shown as solid curves in Figures 2.11

and 2.12. The very satisfactory level of agreement between theory and exper-

iment, as demonstrated in these gures, suggests that the model can predict

0.4

0.1

min

, mJ

100

0.6 0.8

Equivalence ratio

100

150

Quiescent mixtures

P = 100 kPa

= 1.5

eory

SMD, µm

1 1.2

Figure 2.11

Minimum ignition energies of quiescent heavy fuel oil and air mixtures for various mean drop

sizes. P = 100 kPa, T

= 290 K. (From Ballal, D.R. and Lefebvre, A.H., Proceedings of the Royal

Society, London Series A, 364 (1717), 277–94, 1978.)

Combustion Fundamentals 61

with fair accuracy the effect of variations in fuel volatility, mean drop size,

and air pressure on minimum ignition energy. It also supports the basic

assumption of the model, namely, that over a wide range of test conditions

fuel evaporation is the rate-controlling step.

Although the above equations for d

in heterogeneous fuel–air mixtures

were derived for quiescent mixtures, they may be applied to owing mix-

tures in combustion systems without much loss of accuracy. This is because,

except for the very largest drops, most of the fuel spray is airborne, and the

relative velocity between the fuel drops and the surrounding air or gas is too

small to appreciably enhance either the rate of fuel evaporation or the rate of

heat loss from the spark kernel.

In a later study, Ballal and Lefebvre [45] extended the model described

above to include (1) the effects of nite chemical reaction rates, which are

min

, mJ

100

Pressure, Pa

φ = 0.65

U = 0

SMD = 60 µm

eory

Heavy fuel oil

Iso-octane

Gas oil

Diesel oil

2×10

Figure 2.12

Effect of air pressure on minimum ignition energy. ϕ = 0.65, SMD = 60 µm, T

= 290 K, U = 0.

(From Ballal, D.R. and Lefebvre, A.H., Proceedings of the Royal Society, London Series A, 364 (1717),

277–94, 1978.)

62 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

known to be signicant for very well atomized fuels at low pressures and

low equivalence ratios; and (2) the presence of fuel vapor in the mixture

owing into the ignition zone. Thus, the model has general application to

both quiescent and owing mixtures of air with either gaseous, liquid, or

evaporated fuel or any combination of these fuels. Equations for quenching

distance were derived to cover all the conditions likely to be encountered

in practical combustion systems. Thus, for example, with chemical effects

included, Equation 2.35 becomes

AstL

ln 1+

(

)

























ρφ

(2.38)

The validity of the general model was tested experimentally for both qui-

escent and owing mixtures. Figure 2.13 shows measured values of E

min

plotted against equivalence ratio ϕ for quiescent mixtures of heavy fuel oil

0.4

100

min

, mJ

0.5 0.6 0.7

Equivalence ratio

P = 100 kPa

= 1.5

100

150

SMD,µm

Chemical eﬀects included

0.8 0.9 1.0 1.1

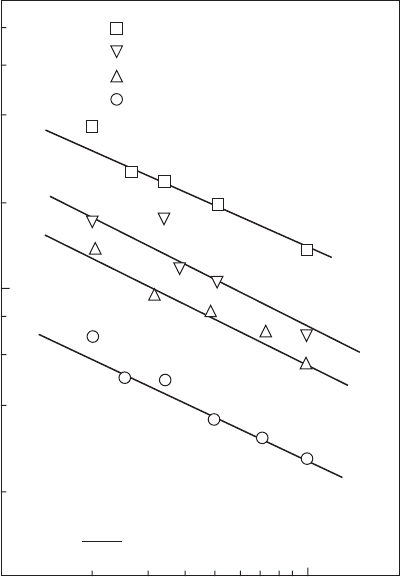
Figure 2.13

Improvements in correlation resulting from inclusion of chemical effects. Heavy fuel oil, U = 0.

(From Ballal, D.R. and Lefebvre, A.H., Eighteenth Symposium (International) on Combustion, The

Combustion Institute, Pittsburgh, PA, 1737–46, 1981.)

Combustion Fundamentals 63

and air. The gure shows that the general model provides a good t to the

data over a range of SMDs from 40 to 150 µm.

Figure 2.14 shows the inuence of pressure on E

min

for four different fuels

with a mean drop size of 60 µm when sprayed into a owing airstream.

Again, the excellent correlation achieved by including both chemical and

evaporation effects is apparent in this gure.

In general, where evaporative effects are dominant, Equations 2.36 and 2.37

indicate for both quiescent and owing mixtures that E

min

αP

–0.5

. However,

when chemical effects govern, Equations 2.30 and 2.32 show that E

min

αP

–2.0

for the extreme case where ame speed is independent of pressure. Thus,

for both stagnant and owing heterogeneous mixtures, the pressure expo-

nent of E

min

always lies between –0.5 and –2.0 and depends on the relative

Heavy fuel

Chemical effects included

400

200

min

, mJ

100

0.15 0.2 0.3 0.4

Pressure, Pa × 10

–5

0.6 0.8 1.0

i-octane

Gas oil

Diesel oil

Figure 2.14

Improvements in correlation resulting from inclusion of chemical effects. U = 15 m/s, ϕ = 0.65,

SMD = 60 µm. (From Ballal, D.R. and Lefebvre, A.H., Eighteenth Symposium (International) on

Combustion, The Combustion Institute, Pittsburgh, PA, 1737–46, 1981.)

64 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

importance of evaporative and chemical effects. In general, any change that

enhances the role of reaction kinetics, such as a reduction in pressure and/or

equivalence ratio, tends to increase the dependency of E

min

on pressure.

2.12 Spontaneous Ignition

Spontaneous ignition, or autoignition, is a process whereby a combustible

mixture undergoes a chemical reaction that leads to the rapid evolution of

heat in the absence of any concentrated source of ignition, such as a ame

or spark. In the lean-premix combustor, and other types of low-emissions

combustors where fuel and air are premixed before combustion, spontane-

ous ignition must be avoided at all costs because it could damage combustor

components and produce unacceptably high levels of pollutant emissions.

Spontaneous ignition delay may be dened as the time interval between

the creation of a combustible mixture, say by injecting fuel into a owing

airstream at high temperature, and the onset of ame. Ignition delay times

are often correlated using the Wolfer equation [46].

tP T

(

)

−

0434650

119

.exp ,

(2.39)

where t

is the ignition delay time in ms, P is the pressure in bars, and T

the initial mixture temperature in degrees K. To accommodate the effects

of equivalence ratio on ignition delay times, Equation 2.39 may be modied

and expressed in a more general form as

tAPERT

(

)

−−

φ exp,

(2.40)

where A, n, and m are constants that are determined experimentally, P is

the pressure (usually expressed in atmospheres or bars), E is the activation

energy in cal/g mol, R is the gas constant (1.986 cal/g mol), and T

is the ini-

tial temperature of the fuel–air mixture in degrees K.

In view of their practical importance, measurements of spontaneous

ignition delay time have been conducted for many fuels over wide ranges

of ambient conditions and in a variety of test vehicles, including rapid-

compression machines, shock tubes, and continuous ow devices. The test

methods employed and the results obtained are described in reviews by

Mullins [47], Spadaccini and Te Velde [48], Goodger and Eissa [49], and

Lundberg [50].

Freeman, Cowell, and Lefebvre [51,52] used a continuous ow apparatus

to measure autoignition delay times. Twenty-ve equispaced fuel-injection

points ensured rapid mixing of gaseous fuel or fuel vapor with heated air at

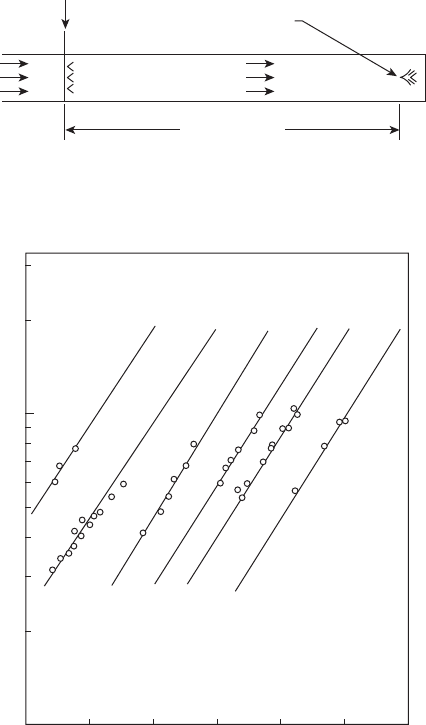
Combustion Fundamentals 65

entry to the test section. The concept is shown schematically in Figure 2.15,

where the ignition delay time is dened as the length L divided by the gas

velocity U. This method has the advantage that when spontaneous ignition

occurs, it does so under conditions that closely simulate those prevailing

in the premixing passages of advanced combustors. Some of the results

obtained for propane– and methane–air mixtures are shown in Figures 2.16

through 2.18.

Hot

air

Fuel/air

mixture

S. I. flame front

Delay length, L

Fuel

Figure 2.15

Basis of ignition delay time measurement technique. (Reprinted from Freeman, G. and

Lefebvre, A.H., Combustion and Flame, 58(2), 153–62, 1984. With permission from Elsevier, Inc.)

1.00

100

200

300

Delay time, ms

1.04 1.08 1.12

1000/T

, K

–1

1.16 1.20 1.24

Propane-air mixtures

φ = 0.4

Pressure, atmos

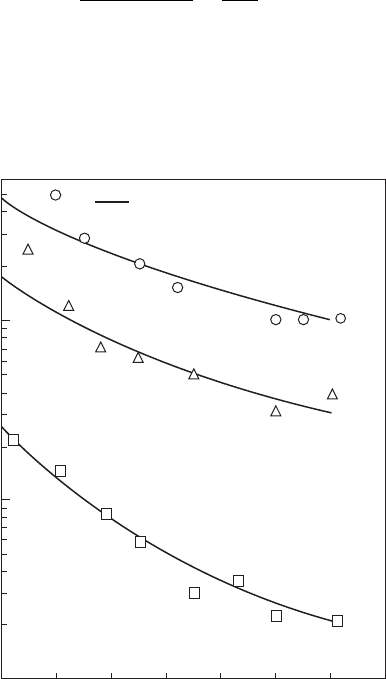
Figure 2.16

Inuence of pressure and temperature on ignition delay times of propane-air mixtures. (From

Cowell, L.H. and Lefebvre, A.H., SAE Paper 860068, 1986. With permission.)

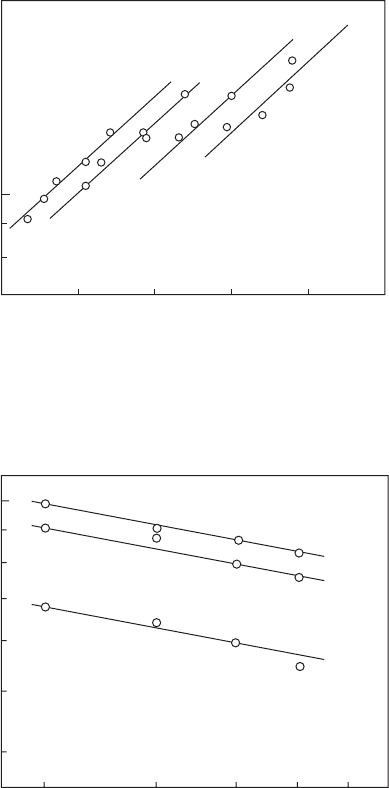
66 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

The form of Equation 2.40 suggests that a plot of ln t

vs. 1/T

should yield

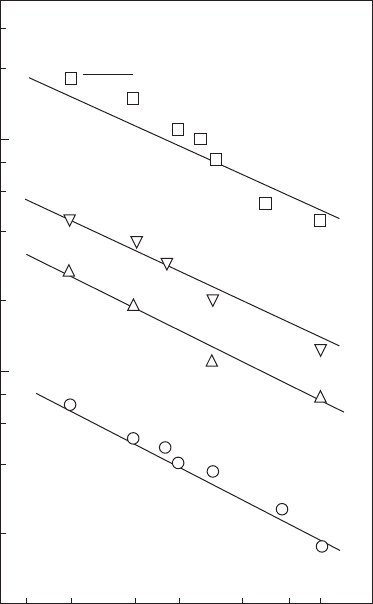
a straight line with a positive slope, and this is borne out by the results pre-

sented in Figures 2.16 and 2.17. The values of E given by the slopes of the lines

in these gures are 38.2 kcal/g mol for propane and 25.0 kcal/g mol for meth-

ane. For kerosine (Jet A), the value of E was found to be 29.6 kcal/g mol.

1.00

100

Delay time, ms

200

Pressure, atm

Methane – air mixtures

φ = 0.4

1.02 1.04

1000/T

, K

–1

1.081.06 1.10

Figure 2.17

Inuence of pressure and temperature on ignition delay times of methane–air mixtures. (From

Cowell, L.H. and Lefebvre, A.H. SAE Paper 860068, 1986. With permission.)

0.2

Delay time, ms

100

0.3 0.4

Equivalence ratio, φ

Methane – air mixtures

= 1000 K

τα φ

–0.19

Pressure, atm

0.5 0.7

Figure 2.18

Inuence of mixture strength on ignition delay times of methane–air mixtures. (From Cowell,

L.H. and Lefebvre, A.H., SAE Paper 860068, 1986.)

Combustion Fundamentals 67

The inuence of pressure on t

is of great practical interest in view of the

continuing trend toward engines of higher pressure ratio. Its importance is

apparent from inspection of the experimental data plotted in Figures 2.16

and 2.17, which show a pronounced effect of pressure on t

. Analysis of these

and other data [53] led to values for n in Equation 2.40 of 1.2 for propane and

1.0 for both methane and kerosine (see Table 2.1).

There appears to be little agreement between different workers in regard

to the inuence of equivalence ratio on ignition delay time. Mullins [47]

observed no effect, whereas Ducourneau [54] and Spadaccini and Te Velde

[48] both found strong effects. Lefebvre et al. [53] examined the inuence of ϕ

on t

for several fuels and found in all cases that delay times were reduced by

an increase in equivalence ratio. Figure 2.18 is typical of the results obtained.

It shows for methane that t

αϕ

–0.19

. For propane and aviation kerosine, the

measured values for m were higher at 0.30 and 0.37, respectively.

The explanation for the marked lack of consistency between different

workers in regard to the inuence of ϕ on t

probably lies in the mode of

fuel injection. With liquid fuels, there is always the potential for stoichio-

metric combustion in regions close to the evaporating spray. Thus, measured

ignition delay times may be close to those for stoichiometric mixtures, even

though the average equivalence ratio of the mixture differs appreciably from

the stoichiometric value. Just how close will depend on the drop-size distri-

bution in the spray, because this governs the initial rate of fuel evaporation

and also the length of time that stoichiometric “streaks” of fuel–air mixture

can survive. The number of fuel-injection points is also important. In this

context, it is of interest to note that Tacina [55] obtained much more consis-

tent autoignition data with a single orice injector than with a 41-hole injec-

tor, which ostensibly should have provided a more uniform fuel–air mixture.

Presumably, this was because with a single injector the rate of fuel–air mix-

ing was so slow that the bulk of the prereactions leading up to the onset of

ignition took place in near-stoichiometric mixtures, regardless of the aver-

age equivalence ratio. With gaseous fuels, the inconsistencies associated

with slow fuel evaporation are no longer present, but the measured ignition

delay times are still very dependent on the time required for the fuel and air

to form a combustible mixture. As with liquid fuels, the longer the mixing

time, the closer the measured ignition delay times will approach stoichio-

metric values.

TABLe 2.1

Experimental values of constants in

Equation 2.40

Fuel E (kcal/g mol) n m

Propane 38.2 1.2 0.30

Methane 25.0 1.0 0.19

Kerosine 29.6 1.0 0.37

68 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

Another probable reason for the conicting evidence of the effect of

equivalence ratio on ignition delay time is that in continuous ow experi-

ments the fuel is almost invariably at a much lower temperature than the

hot airstream into which it is injected. This has the advantage of closely

simulating the actual engine situation but, from a fundamental viewpoint,

it has the drawback that any change in ϕ must also change the temperature

in the initial fuel–air mixing zone(s). As ignition delay time is exponentially

dependent on temperature, the effect of a small change in temperature in

these localized mixing zone(s) could be very pronounced and could largely

offset the effect of the corresponding change in ϕ on ignition delay time.

Note that the effect of this change in temperature on t

, will always be such

as to oppose the change in t

caused by the change in ϕ. The net result is

that measurements of t

, carried out in continuous ow devices will always

underpredict the effect of a change in ϕ on t

by an amount that depends on

the difference in temperature between the hot airstream and the injected

fuel gas or vapor.

Most analyses and equations for ignition delay time ignore the effects

of fuel vaporization, which is reasonable under conditions where the fuel

evaporation time is appreciably shorter than the mixing and reaction times.

However, it is important to bear in mind that spontaneous ignition delay

times are affected by both physical and chemical processes. For liquid fuels,

the physical delay is the time required to heat and vaporize the fuel drops

and to mix the fuel vapor in ammable proportions with the surrounding

air. The chemical delay is the time interval between the formation of a am-

mable mixture and the appearance of ame. Thus, the physical processes

are important in the early stages of spontaneous ignition, while in the later

stages the chemical processes become over-riding.

Rao and Lefebvre [56] have proposed a model for spontaneous ignition

that takes both chemical and physical effects into account and has general

application to both homogeneous and heterogeneous mixtures, including

situations where both fuel drops and fuel vapor are initially present. This

model leads to an equation where the ignition delay time, t

, is derived as the

sum of the times required for evaporation and chemical reaction. Calculated

values of t

from this equation show that fuel evaporation times are negligibly

small in comparison with chemical reaction times for well atomized, highly

volatile fuels, especially at conditions of low pressure and temperature. They

also show that fuel evaporation times become increasingly signicant with

increases in pressure and temperature.

When calculating ignition delay times for liquid fuels, it is customary to

disregard the fuel evaporation time. As discussed above, this is permissible

for well-atomized volatile fuels injected into airstreams at relatively low pres-

sures. However, it is important to recognize that for certain ultralow NO

com-

bustors (e.g., catalytic or lean premixed prevaporized (LPP)) when operating at

high-power conditions corresponding to high air pressures and temperatures,

the fuel evaporation time could be so long in relation to the chemical delay

Combustion Fundamentals 69

time that spontaneous ignition of the initial fuel vapor might occur before the

remainder of the fuel spray has had time to evaporate. Very ne fuel atomiza-

tion and rapid vapor–air mixing will be required to combat this problem.

In summary, autoignition data are very apparatus-dependent and, in par-

ticular, very fuel injector-dependent. Considerable caution should be exer-

cised in comparing and selecting autoignition data and in no circumstances

should experimentally derived equations for t

, be extrapolated to pressures

and temperatures outside the range of their experimental verication. Such

extrapolations could lead to erroneous results because differences in reaction

routes may occur over different levels of temperature and pressure. When

liquid fuels are injected into air at high pressures and temperatures, very

ne atomization is needed to promote rapid vaporization, thereby reducing

the risk of spontaneous ignition in the fuel preparation zone.

2.13 Flashback

An intrinsic feature of all premixed-fuel combustion systems is a tendency

toward ashback. Flashback occurs when the ame travels upstream from

the combustion zone into the premixing sections of the combustor. This

upstream propagation of ame takes place whenever the ame speed exceeds

the approach ow velocity.

Three main types of ashback have been identied: (1) ashback occur-

ring in the free stream, (2) ashback occurring through the low-velocity

ow in the boundary layer along the walls of the premixing section, and

(3) ashback driven by combustion-induced vortex breakdown (CIVB) in

swirl-stabilized combustors. Any mechanism may involve homogeneous

and/or heterogeneous reactions.

The most obvious free-stream mechanism would be the occurrence of

ashback due to a ow reversal in the bulk ow through the combustor.

This ow reversal could be a result of compressor surge or combustion insta-

bility. Flashback can also occur in the absence of ow reversal if the tur-

bulent ame speed through the gas in a premixing section is greater than

the local bulk velocity. Lean combustion tends to reduce ame speeds, but

other factors associated with the engine cycle, such as high temperatures,

pressures, and turbulence levels, and preignition reactions in the gas due

to appreciable residence times at high temperature levels, cause increased

ame speed. Therefore, ame speeds may be sufciently high to necessitate

increasing the minimum allowable velocity in premix-prevaporize sections

to fairly high levels to avoid disturbances to the combustion process.

The boundary-layer mechanism involves ashback through retarded ow

in a boundary layer. Important relevant parameters include the wall tem-

perature and temperature distribution, and the boundary-layer structure,