Lefebvre A.H., Ballal D.R. Gas Turbine Combustion: Alternative Fuels and Emissions

Подождите немного. Документ загружается.

180 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

region [28,35]. According to Zukowski and Marble [28], ignition of the fresh

mixture occurs in the shear layer when it is turbulently mixed with combus-

tion products from the recirculation zone. The burning mixture then ows

downstream through the shear layer, where it ignites neighboring mixture

kernels. When it reaches the end of the wake region, some of the burning

mixture continues to ow downstream, and the remainder is entrained into

the recirculatory ow, which conveys it upstream to mix with and ignite the

shear layer. A ame is anchored on the bafe through continuation of this

process. Flame extinction occurs when the fresh mixture does not spend

enough time in the shear layer to be ignited by the hot recirculation zone.

Thus, the criterion for blowout is that the ignition delay time be equal to the

residence time in the shear layer adjacent to the recirculation zone.

Which of these two basic approaches has the most fundamental signi-

cance and relevance to ame stabilization is uncertain but, fortunately, is

of academic interest only as far as the development of a suitable correlation

for weak extinction is concerned. This is because the time spent by the

fresh mixture in the shear layer, and the residence time of the combustion

products in the recirculation zone, are both proportional to the characteris-

tic dimension of the ameholder, D

. Since the material entering the recir-

culation zone at its downstream edge has already passed through the shear

layer, it would seem more logical to dene the residence time as the sum

of the times spent in the shear layer and the recirculation zone. However,

because this total time is also proportional to D

, this assumption does not

change the resulting correlation. This, of course, is why many workers,

who appear to base their analyses on a seemingly different set of assump-

tions, all eventually arrive at the same general conclusion, namely, that the

equivalence ratio at blowout is a function of

UP D

, and

or exp(T

/z),

where U is the velocity in the plane of the ameholder, P is pressure, and

is the inlet gas temperature. For information on the values x, y, and z,

obtained experimentally before 1960, reference should be made to the sur-

vey papers of Longwell [36] and Herbert [37]. The purpose of this brief dis-

cussion is to point out that, regardless of how simple or sophisticated the

assumptions employed in its derivation, the best correlating parameter is

one that is based on sound principles and has the greatest ease and breadth

of application.

The general approach adopted by Ballal and Lefebvre [32,34] for homoge-

neous fuel–air mixtures was to assume that ame blowout occurs when the

rate of heat liberation in the combustion zone becomes insufcient to heat

the incoming fresh mixture up to the required reaction temperature. With

heterogeneous mixtures, an additional factor is the time required for fuel

evaporation. For fuel sprays of low volatility and large mean drop size, this

time is relatively long and is often the main factor limiting the overall rate of

heat release. Thus, in the analysis of lean blowout limits, it is appropriate to

consider homogeneous mixtures rst and then to examine how the results

obtained should be modied to take account of fuel evaporation.

Combustion Performance 181

5.9.1 Homogeneous Mixtures

Following Longwell et al. [27], Ballal and Lefebvre [32] viewed the reaction

zone of a bluff-body ameholder as a homogeneous chemical reactor in

which the temperature and chemical composition are constant throughout.

Their proposed model is based on the notion that ame extinction occurs

when the amount of heat needed to ignite the fresh mixture being entrained

into the wake region just exceeds the amount of heat liberated by combus-

tion in that zone. The rate of entrainment of fresh mixture into the wake

region is assumed to be proportional to the product of gas density, surface

area, and the velocity difference between the fresh mixture owing over the

wake region and the adjacent, co-owing combustion products. This veloc-

ity difference is proportional to the velocity of the ow over the edge of the

bafe, which is equal to U / (1 − B

). If it is further assumed that for a conical

ameholder of diameter D, the surface area available for the entrainment of

fresh mixture is proportional to D

, then



mDUB∝−ρ

1/( ).

(5.22)

The maximum airow rate corresponding to ame blowout is derived

from global reaction rate considerations [32] as



mVPT

max

.exp(/ ).= 193150

125625

(5.23)

Equating Equations 5.22 and 5.23 and substituting for ρ = P/ RT and

∝

leads to

oo cg

∝

−













PT TDB

025

016

1501

exp( /)()

(5.24)

This equation shows that the weak extinction value of ϕ is affected mainly

by temperature, to a lesser extent by velocity, and hardly at all by pres-

sure. An increase in the characteristic dimension, D

, of the ameholder

always improves the weak extinction performance (i.e., reduces ϕ

), pro-

vided that the increase in D

is not accompanied by an increase in the

blockage ratio B

. If this occurs, then the increase in D

still improves the

weak extinction performance, but only up to a certain value of B

, beyond

which the performance starts to decline. For a conical bafe mounted in a

circular pipe, the critical value of blockage ratio is 33% (that is, B

= 0.33).

Equation 5.24 also indicates that, for a constant value of D

, an increase in

caused, say, by a reduction in pipe diameter or by the introduction of

more ameholders in the same plane, always has an adverse effect on weak

extinction performance.

182 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

As mentioned earlier, the true characteristic dimension of a ameholder

from a stability viewpoint is not its geometric size, but the corresponding

“aerodynamic” value measured downstream of the bafe in the plane of max-

imum aerodynamic blockage. The ratio of the aerodynamic blockage B

to the

geometric blockage B

depends on the forebody shape of the ameholder. The

more streamlined the forebody shape, the lower the ratio of B

to B

[29,38].

The predictions of Equation 5.24 in regard to the inuence of ameholder

dimensions and operating conditions on weak extinction limits show good

agreement with the results obtained by Ballal and Lefebvre over wide ranges

of pressure, temperature, velocity, and stabilizer dimensions, as demon-

strated in Figure 5.24. They also show good qualitative agreement with the

experimental data obtained by other workers for bafe-stabilized ames

[27–30,39,40].

5.9.2 Heterogeneous Mixtures

Equation 5.24 may also be used to predict the lean blowout limits of com-

bustion systems supplied with heterogeneous fuel–air mixtures, provided

that the rate of fuel evaporation is sufciently high to ensure that all the

fuel is fully vaporized within the primary combustion zone. If the fuel does

not fully vaporize, then clearly the “effective” fuel/air ratio will be lower

than the nominal value. However, if the fraction of fuel that is vaporized is

0.34

0.8

0.7

0.6

0.5

0.4

0.4 0.5 0.6 0.7 0.8

0.25

0.11

0.04

Propane-air mixture

(all test data)

(φ

)

measured

(φ

)

predicted

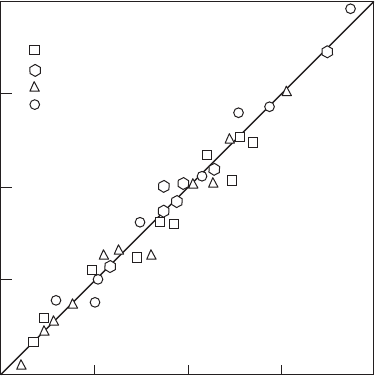
Figure 5.24

Comparison of measured and predicted values of weak extinction limits. (From Ballal, D.R.

and Lefebvre, A.H., Journal of Engineering for Power, 101(3), 343–348, 1979. With permission.)

Combustion Performance 183

known, or can be calculated, it can be combined with Equation 5.24 to yield

the fuel/air ratio at lean blowout, i.e.,

φφ

WE WE f

heterogeneoushomogeneous

(

)

(

)

/,f

(5.25)

where f

is the fraction of fuel that is vaporized within the primary zone.

From analysis of the factors governing the rate of evaporation of a fuel

spray, it was found [9,33] that

fVfmD

fgceff pz Ao

= 8

ρλ/,



(5.26)

where f

is the fraction of the total airow rate,



, that enters the primary

zone.

If the value of f

determined from Equation 5.26 exceeds unity, this means

that the time required for fuel evaporation is less than the time available, so

the fuel is fully vaporized within the recirculation zone, f

should then be

assigned a value of 1.0, so that

φφ

WE WE

heterogeneoushomogeneous

(

)

(

)

The validity of this approach to the determination of weak extinction lim-

its for ames supplied with owing heterogeneous fuel–air mixtures may

be tested by comparing measured values of ϕ

with the corresponding pre-

dicted values from Equations 5.24 through 5.26. This is done in Figures 5.21

through 5.23, in which the full lines represent the predicted values from

these equations [33]. Clearly, the level of agreement between the measured

and predicted values is generally satisfactory, thus conrming the basic

premise of the model.

5.10 Flame Stabilization in Combustion Chambers

The designer has very little control over the amount of fresh mixture that is

entrained into the recirculation zone of a bluff-body ameholder. Usually,

this amount represents only a very small fraction of the mainstream ow,

a fraction that varies markedly with changes in air velocity and tempera-

ture [41]. With main combustors, however, air enters the recirculation zone

through various apertures in the liner wall, and the designer can control

the amount of air participating in primary combustion to within fairly close

limits by proper selection of the number, size, and type of aperture.

Figure 5.25a shows the type of primary zone employed in most tubu-

lar combustors. The essential feature, as far as the stabilization process is

184 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

concerned, is the toroidal ow reversal that is created and maintained by air

entering through swirl vanes located around the fuel injector and through

a single row of holes in the wall of the liner. In addition to its main role as

the major heat-release zone of the chamber, an important function of the

primary zone is to recirculate burned and burning gases to mix with the

incoming air and fuel. By this means, a mechanism of continuous ignition is

established, and combustion can be sustained over wide ranges of pressure,

velocity, and fuel/air ratio.

Figure 5.25b shows a typical primary-zone conguration for an annular

combustor in which the primary air feed is supplemented appreciably by

lm-cooling air in the dome region and, to an increasing extent, by the air

employed in the fuel-preparation process.

Flame stabilization in gas turbine combustors has not been subjected to

the same experimental and theoretical study as in bluff-body ameholders,

but, as a general rule, maximum stability is achieved by injecting the pri-

mary air through a small number of large holes. This is because large holes

produce large jets and large-scale ow recirculations that provide ample

time for combustion. However, for a given air mass ow rate, an increase in

hole size can be obtained only at the expense of a reduction in the number

of holes. Although no rm guidelines have been laid down for the optimal

number of liner holes for annular combustors, one opposing pair of holes

per fuel injector should be regarded as the absolute minimum; twice that

number would be preferable.

For aircraft engines, lean blowout limits are especially important when the

aircraft is descending through inclement weather with the engine idling. At

this ight condition, the combustor AFR is typically around 120, but a lean

blowout AFR of around 250 is usually specied in order to provide a safety

margin for engine to engine variations, fuel control tolerances, and the pos-

sible ingestion of water and/or ice.

5.10.1 influence of Mode of Fuel injection

One of the key factors governing lean blowout limits is the mode of fuel injec-

tion. The poor fuel distribution of pressure-swirl atomizers of the simplex

(a)

(b)

Figure 5.25

Typical primary-zone congurations.

Combustion Performance 185

or dual-orice type ensures that some combustion takes place at mixture

strengths that are appreciably richer than the average value. This means

that, even when the nominal fuel/air ratio falls to well below the normal

lean blowout limit, the ame can still survive due to the presence, within the

burning zone, of pockets of near-stoichiometric mixtures. This is why pres-

sure atomizers are noted for wide burning limits—in particular, for good

lean blowout values (typically around 1000 AFR). By contrast, the airblast

atomizer, which provides much better mixing of fuel and air, is characterized

by fairly narrow burning limits (a typical lean blowout limit is around 250

AFR). Methods of overcoming the poor lean blowout performance of airblast

atomizers include the use of piloting devices as employed, for example, in

the hybrid or piloted airblast atomizer (see Chapter 6) and staged fuel injection

(see Chapter 9). Nowhere is the problem of ame extinction more important

than in the lean premix prevaporize combustor, which must, of necessity,

always operate close to the lean blowout limit.

5.10.2 Correlation of experimental Data

For gas turbine combustors, the lean blowout limit is usually expressed in

terms of overall combustor fuel/air ratio rather than equivalence ratio, which

is more common for bluff-body ameholders.

From an analysis of lean blowout data acquired from a large number of air-

craft combustion chambers [12–17], the following equation for lean blowout

fuel/air ratio, q

LBO

, was derived [11]

LBO



























300

exp( /)λλ













(5.27)

where D

is the mean drop size relative to that for JP4, H

is the lower caloric

value relative to that for JP4, and λ

is the effective evaporation relative to

that for JP4.

A is a constant whose value depends on the geometry and mixing charac-

teristics of the combustion zone and also on the amount of air employed in

primary combustion [11]. Having determined the value of A for any given

combustor at any convenient test condition, Equation 5.27 may then be used

to predict the lean blowout fuel/air ratio at any other operating condition.

The rst term on the right hand side of Equation 5.27, which contains com-

bustion volume, is the only term that can be varied at the discretion of the

designer. The second term represents the combustor operating conditions.

The third term embodies the relevant fuel-dependent properties of mean

drop size, effective evaporation constant, and the heating value of the fuel.

For each combustor for which lean blowout data were available [11], a value

of A was chosen for insertion into Equation 5.27 that gave the best t to the

experimental data. These values are listed in Table 5.1. The satisfactory level

186 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

of correlation achieved is illustrated for three combustors in Figures 5.26

through 5.28.

The especially low value of A shown in Table 5.1 for the TF41 combustor

can be attributed to its excellent atomizing characteristics at low fuel ows,

stemming from the use of an exceptionally low primary nozzle ow number.

The high value of A obtained for the J85 combustor is attributed to a design

modication made during its development that introduced additional air

into the front end of the liner as a smoke-reduction measure.

TABLe 5.1

Values of A and B Employed

in Equations 5.27 and 5.29

Engine A B

J 79-17A 0.042 0.20

J 79-17C 0.031 –

F 101 0.032 0.090

TF 41 0.013 0.63

TF 39 0.037 0.21

J 85 0.064 0.18

TF 33 0.025 0.27

F 100 0.023 0.17

TF 41

024

LBO

(predicted), g/kg

LBO

(measured), g/kg

6810

TF 41

= 62–342 kPa

= 297–575 K

= 0.337–1.131 kg/s

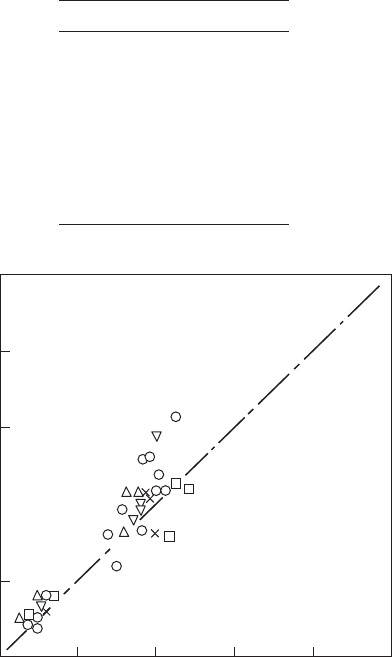
Figure 5.26

Comparison of measured and predicted values of q

LBO

for a TF 41 combustor. (From Lefebvre, A.H.,

Journal of Engineering for Gas Turbines and Power, 107, 24–37, 1985. With permission.)

Combustion Performance 187

J 85

= 44–152 kPa

= 250–366 K

= 1.0–4.81 kg/s

048121620

LBO

(predicted), g/kg

LBO

(measured), g/kg

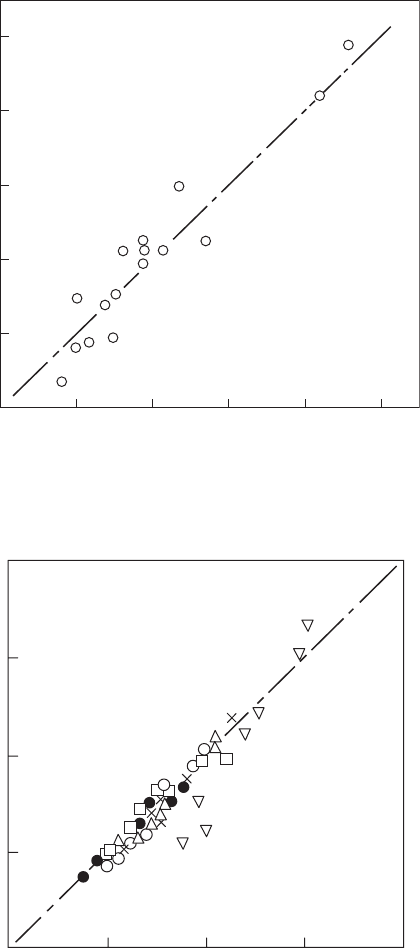
Figure 5.27

Comparison of measured and predicted values of q

LBO

for a J 85 combustor. (From Lefebvre, A.H.,

Journal of Engineering for Gas Turbines and Power, 107, 24–37, 1985. With permission.)

J 79-17C

= 101 k P

= 0.318 kg/s

= 238–278 K

= 238–278 Ka

23456

LBO

(predicted), g/kg

LBO

(measured), g/kg

Figure 5.28

Comparison of measured and predicted values of q

LBO

for a J 79 combustor. (From Lefebvre, A.H.,

Journal of Engineering for Gas Turbines and Power, 107, 24–37, 1985. With permission.)

188 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

Equation 5.27, which contains a drop-size term, is clearly inappropriate for

combustors in which the fuel is fully vaporized and mixed with air upstream

of the combustion zone. For such combustors, a more suitable expression is

given by substituting for



mUA=ρ

into Equation 5.24 to obtain

qCmVPT

LBO Ac

{}



/exp(/ ).

125

016

100

(5.28)

At the present time, the available data on the lean blowout limits of lean-

premix combustors is too sparse to allow an accurate determination of the

constant C, which must therefore be determined experimentally for each

combustor.

5.11 Ignition

Of prime importance to the gas turbine is the need for easy and reliable

lightup during ground starting, while the engine is being cranked up to its

self-sustaining speed. With the aircraft gas turbine, an additional requirement

is for rapid relighting of the chamber after a ameout in ight. Under adverse

climatic conditions, or on takeoff from a wet runway, where there is a risk of

ingestion of excessive amounts of water or ice, the ignition system must also

be capable of continuous operation in order to ensure immediate relighting

of the engine in the event of ame extinction.

The ignition of a combustible mixture may be accomplished by various

means, but in the gas turbine it is usually effected by means of an electric

spark. Large amounts of energy are needed to ignite the heterogeneous and

highly turbulent mixtures owing at velocities of the order of 25 m/s.

Since the early 1970s, many theoretical and experimental studies have

been carried out on the inuence of fuel and ow parameters on minimum

spark energy in owing mixtures of fuel drops and air. The main ndings of

these studies are described and discussed in Chapter 2. A useful outcome of

this work is that we now have a better conceptual understanding of the basic

ignition process and a sound theoretical foundation for relating ignition

characteristics to all the relevant operating variables. The results obtained

generally conrm practical experience in showing that ignition is made eas-

ier by increases in pressure, temperature, and spark energy, and is impaired

by increases in velocity, turbulence intensity, and fuel drop size. With liquid

fuels, ignition performance is markedly affected by fuel properties through

the way in which they inuence the concentration of fuel vapor in the imme-

diate vicinity of the igniter plug. These inuences arise mainly through the

effect of volatility on evaporation rates, but also through the effect of viscos-

ity on mean fuel drop size. The amount of energy required for ignition is very

much larger than the values normally associated with gaseous fuels. Much

of this extra energy is absorbed in the evaporation of fuel droplets, the actual

Combustion Performance 189

amount depending on the distribution of fuel throughout the primary zone

and on the quality of atomization.

The continuing trend toward engines of higher compression ratio and

higher primary-zone velocities has produced a gradual deterioration in the

environmental conditions of the ignition unit and igniter plug. At the same

time, there has been an increasing demand for improvements in the perfor-

mance, life, and reliability of ignition equipment. Thus, the problem of igni-

tion, particularly in aircraft engines, is one of continuing importance and

merits discussion in some detail.

5.12 Assessment of Ignition Performance

The ignition performance of an aircraft engine is usually expressed in terms

of the range of ight conditions over which combustion can be re-established

after a ameout at altitude. To determine the relighting capabilities of an

engine, it is customary to carry out a series of combustor rig tests, in which

the inlet parameters are varied to reproduce a range of ight conditions. The

test procedure is very similar to that employed in deriving stability limits.

For constant combustor inlet pressure, temperature, and air mass ow, igni-

tion is attempted at various values of fuel/air ratio. Successful ignition is

indicated by continued burning after the igniting source has been switched

off. A maximum time, which is normally 10 seconds but could be as low as

3 seconds, is allowed for each ignition attempt. The procedure is repeated for

a range of mass ows until a complete ignition loop can be drawn. A typical

loop for an aircraft combustion chamber is shown in Figure 5.29. Usually,

0.03

0.02

Ignition possible

within loop

= Constant

Stability

loop

0.01

Air mass flow rate, kg/s

Fuel/air ratio

0 0.25 0.5 0.75 1.0

Figure 5.29

Typical combustor ignition loop.