Lee K.K. Lectures on Dynamical Systems, Structural Stability and Their Applications
Подождите немного. Документ загружается.


biochemical
reactions
and
can
also
provide
some
understanding,
at
least
qualitatively,
the
Belousov-Zhabotinski
(B-Z)
reactions
where
both
temporal
and
spatial
oscillations
have
been
observed
[Hastings
and
Murray
1975].
Kuramoto
and
Yamada
[1976]
were
first
to
propose
the
possibility
of
turbulence-like
behavior
of
reactant
concentrations
in
oscillatory
chemical
reactions.
Their
discussion
was
based
on
the
reduced
form
of
B-Z
equations.
Schimitz,
Graziani,
and
Hudson
[1977]
recently
published
experimental
data
obtained
with
the
B-Z
reaction
which
showed
evidence
of
chaotic
states.
Olson
and
Degn
[1977]
presented
results
on
chaos
in
a
biochemical
system,
the
horseradish
peroxidase
reaction.
Indeed,
these
studies
were
guided
by
the
pioneer
work
of
Rossler
who
had
shown
that
a
simple
set
of
three
ordinary
differential
equations
could
produce
chaos
[1976].
Consequently,
chaos
is
most
likely
to
be
found
in
laboratory
chemical
reactors.
Subsequently,
Hudson
et
al
[1979]
have
shown
that
an
entire
sequence
of
states,
some
periodic
and
some
chaotic,
could
be
obtained
by
varying
a
single
parameter,
the
flow
rate
or
residence
time.
Similar
behavior
has
since
been
confirmed
by
Turner
et
al
[1981].
Experimental
studies
on
the
B-Z
reactions
continue,
and
the
investigation
of
chaotic
behavior
in
chemical
reactors
is
quite
active.
Indeed,
even
higher
forms
of
chaos,
i.e.,
more
than
one
positive
Liapunov
characteristic
exponent,
is
likely
to
be
found
in
chemical
systems
[Rossler
and
Hudson
1983].
There
have
been
several
studies
in
heterogeneous
systems
governed
by
partial
differential
equations.
The
experiments
were
carried
out
in
an
isothermal
continuous
stirred
tank
reactor
(CSTR).
The
reactants
are
fed
more
recently
by
means
of
precise
constant
volume
pumps.
And
data
are
taken
with
a
platinum
wire
electrode
and
a
bromide
ion
electrode
which
are
connected
to
a
digital
computer.
Data
have
been
obtained
as
a
function
of
flow
rate,
temperature,
and
feed
concentration.
We
shall
limit
our
discussion
to
results
obtained
at
a
single
temperature
354

and
mixed
feed
concentrations.
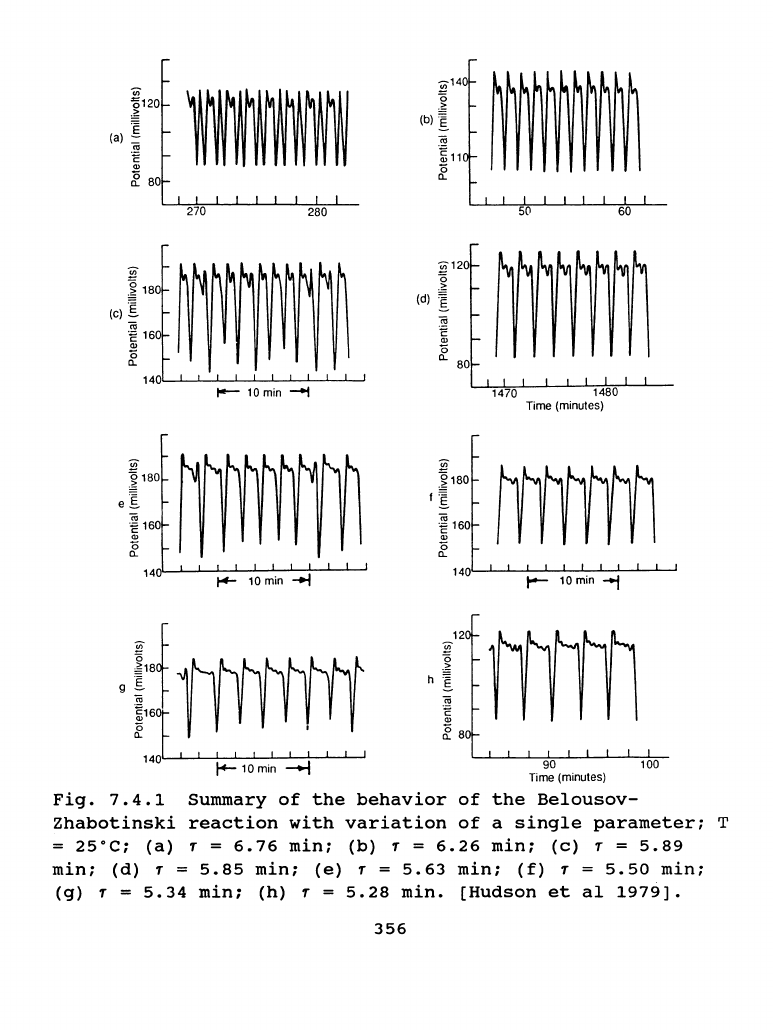
A
portion
of
the
series
of
oscillations
with
the
bromide
electrode
is
shown
in
Fig.7.4.1.
The
oscillations
in
1a
(with
the
residence
time
1
=
6.76
min)
are
alternating
single
and
double
peaks
and
those
in
1b
(1
=
6.26
min)
are
double
peaks.
Both
oscillations
are
periodic
and
stable.
Chaotic
behavior
is
observed
at
1 =
5.89
min
in
1c.
This
behavior
is
reproducible
and
continues
until
the
external
conditions
are
changed.
This
chaos
is
primarily
an
irregular
mixture
of
two
and
three
peaks.
Two
other
regions
of
chaotic
behavior
were
found
in
1e
(1
=
5.63
min.)
and
1g(1
=
5.34
min.).
It
should
be
pointed
out
that
the
ability
of
realistic
B-Z
reaction
models
to
generate
chaos
is
not
yet
completely
clear.
Indeed,
Noyes
and
his
coworkers
[1978]
have
seen
only
periodic
solutions
eventhough
they
have
analyzed
carefully
at
such
models.
On
the
other
hand,
by
modifying
these
equations,
Tomita
and
Tsuda
[1979]
and
Turner
et
al
[1981]
have
obtained
chaos.
Recently
Hudson
et
al
[1984]
have
presented
simulated
results
of
chaos
in
two
single,
irreversible,
exothermic
reaction
whose
reactors
coupled
through
the
heat
transport.
Such
a
single
reaction
has
been
shown
to
produce
sustained
oscillations
in
a
non-adiabatic
continuous
stirred
reactor
by
both
experiments
and
simulations.
It
is
shown
that
for
two
almost
identical
reactors,
if
only
one
parameter,
the
heat
transfer
coefficient
governing
heat
flow
between
the
two
reactors,
is
varied,
the
system
changes
from
periodic,
through
quasiperiodic,
and
finally
becomes
chaotic.
It
is
also
interesting
to
note
that
the
flow
appears
to
have
the
topology
of
a
folded
torus
such
as
that
found
with
the
driven
van
der
Pol
osicillations
[see,
e.g.,
Guckenheimer
and
Holmes
1983].
The
fact
that
chaos
is
found
in
two
coupled
tanks
indicates
that
complex
behavior
may
be
prevalent
in
many
other
systems
involving
reaction-diffusion.
355
!120-
(a)
~
"'
E
CD
~
80
2l
~180
e§.
~16
"
~
,f'i
270
280
I--
10
min
--1
r~
14
J._
_
__LI
_IL_!--1
__LI __LI __L!
_IL_Il-L-.___,
!+-
10
min
-...j
2)12
~
(d)~
"iii
E
"
~
"'
80
~180
·~
~160
"
~
1470 1480
Time (minutes)
90 100
Time (minutes)
Fig.
7.4.1
summary
of
the
behavior
of
the
Belousov-
Zhabotinski
reaction
with
variation
of
a
single
parameter;
=
25"C;
(a)
1
=
6.76
min;
(b)
1
=
6.26
min;
(c)
1
=
5.89
min;
(d)
1
=
5.85
min;
(e)
1
=
5.63
min;
(f)
1
=
5.50
min;
(g)
1
=
5.34
min;
(h)
1
=
5.28
min.
[Hudson
et
al
1979].
356
T

Recently,
Argoul
et
al
[1987]
have
done
experiments
on
the
B-Z
reaction
in
a
continuous
flow
reactor
which
reveal
a
spiraling
strange
attractor
arises
from
the
interaction
of
a
local
subcritical
Hopf
bifurcation
with
a
global
homoclinic
bifurcation.
They
further
point
out
that
the
proximity
of
these
two
bifurcations
justifies
the
application
of
a
theorem
by
Sil'nikov
[1965,1970]
which
ensures
the
existence
of
chaos.
(See
Section
6.3).
Tam
et
al
[1988]
reported
the
first
experimental
observation
of
a new
type
of
spatially
extended
open
chemical
system,
the
Couette
reactor.
This
is
an
effectively
one-
dimensional
reaction-diffusion
system
with
well-defined
boundary
conditions.
The
experiment
reveals
steady,
periodic,
quasiperiodic,
frequency-locked,
period-doubled,
and
chaotic
spatiotemporal
states,
and
qualitatively
agrees
with
the
model,
and
provides
some
insight
into
the
physical
mechanism
for
the
observed
behavior.
In
a
series
of
papers,
Gray
and
Roberts
[1988a,b,c,d]
and
Gray
[1988]
have
developed
a
complete
analysis
of
chemical
kinetic
systems
describable
by
two
coupled
ordinary
differential
equations
and
contain
at
most
three
independent
parameters.
They
considered
the
thermally
coupled
kinetic
oscillators
studied
by
Sal'nikov.
It
should
be
pointed
out
that
Ohtsuki
and
Keyes
[1987]
have
utilized
a
field-theoretic
renormalization-group
method
to
investigate
crossover
behavior
in
nonequilibrium
multicritical
phenomena
of
one-component
reaction-diffusion
systems.
An
expression
for
crossover
exponents
is
derived
and
mean-field
values
of
them
are
obtained
as
a
function
of
n.
As
an
application
to
the
reaction-diffusion
equation,
recently
Conrad
and
Yebari
[1989]
studied
a
simple
model
of
the
dissolution-growth
process
of
a
solid
particle
in
an
aqueous
medium
in
the
stationary
case.
The
resulting
nonlinear
eigenvalue
problem
consists
of
a
reaction-diffusion
equation
in
the
aqueous
medium
limited
by
an
unknown
interface.
The
various
types
of
bifurcation
357

diagrams
depending
on
the
nonlinear
reaction
term
are
described,
and
it
is
also
found
that
more
than
one
solution
exist
in
general.
And
chemical
dissolution
of
a
two-dimensional
porous
medium
by
a
reactive
fluid
which
produces
a
fractal
pattern
is
studied
by
Daccord
(1987].
An
interpretation
of
the
evolution
of
the
injection
pressure
with
time
which
yields
the
fractal
dimension
is
also
presented.
A
reaction-diffusion
equation
related
to
gasless
combustion
of
solid
fuel
has
been
studied.
A
formal
bifurcation
analysis
by
Matkowsky
and
Sivashinsky
(1978]
has
shown
that
solutions
demonstrate
behavior
typical
for
the
Hopf
bifurcation.
A
regorous
tretment
of
this
problem
is
developed
by
Roytburd
(1985].
In
order
to
circumvent
difficulties
involving
a
possible
resonance
with
the
continuous
spectrum,
appropriate
weighted
norms
are
introduced.
A
suitable
version
of
the
Hopf
bifurcation
theorem
is
developed
and
the
existence
of
time
periodic
solutions
is
proven.
Under
general
assumptions,
Kopell
and
Ruelle
(1986]
studied
the
temporal
and
spatial
complexity
of
solutions
to
systems
of
reaction-diffusion
equations.
The
time
averaged
versions
of
complexity
give
upper
bounds
on
entropy
and
Hausdorff
dimension
of
any
attracting
set.
Recently,
Parra
and
Vega
(1988]
have
considered
a
first-
order,
irreversible,
exothermic
reaction
in
a
bounded
porous
catalyst
with
a
smooth
boundary
of
one,
two
or
three
dimensions.
They
considered
the
cases
for
small
Prater
and
Nusselt
numbers,
and
a
large
Sherwood
number;
two
isothermal
models
are
derived.
Linear
stability
analysis
of
the
steady
states
of
such
models
shows
that
oscillatory
instabilities
appear
for
appropriate
values
of
the
parameters.
They
have
also
carried
out
a
local
Hopf
bifurcation
analysis
to
ascertain
whether
such
bifurcation
is
subcritical
or
supercritical.
For
those
readers
who
are
interested
in
the
dynamics
of
shock
waves
andjor
reaction-diffusion
equations,
Smeller
358

[1983]
provides
a
comprehensive
study
of
these
subjects.
A
more
chemically
oriented
discussion
can
be
found
in
Vidal
and
Pacault
[1984].
Numerically,
a
variety
of
time-linearization,
quasi-
linearization,
operator-splitting,
and
implicit
techniques
which
use
compact
or
Hermitian
operators
has
been
developed
for
and
applied
to
one-dimensional
reaction-diffusion
equations
by
Ramos
[1987].
It
is
shown
that
time-
linearization,
quasi-linearization,
and
implicit
techniques
which
use
compact
operators
are
less
accurate
than
second-order
accurate
spatial
discretizations
if
first-order
approximations
are
employed
to
evaluate
the
time
derivatives.
Furthermore,
quasi-linearization
methods
are
found
to
be
more
accurate
than
time-linearization
schemes.
Nonetheless,
quali-linearization
methods
are
less
efficient
because
they
require
the
inversion
of
block
tridiagonal
matrices
at
each
iteration.
Comparisons
among
the
methods
are
shown
in
terms
of
the
L
2
-norm
errors.
Some
improvements
in
accuracy
are
also
indicated.
7.5
competitive
interacting
populations,
autocatalysis,
and
permanence
As
we
have
seen
in
Section
1.1,
the
predator-prey
model
of
interacting
populations,
in
terms
of
Lotka-Volterra
equations,
is
rich
in
structures.
In
this
section,
we
shall
first
discuss
the
effect
of
crowding,
then
we
shall
discuss
in
some
detail
autocatalysis
and
permanence.
Multispecies
and
their
applications
in
biochemical
reactions
will
also
be
discussed
briefly.
Before
we
discuss
any
specific
situations,
it
is
interesting
to
note
that
many
systems
of
nonlinear
differential
equations
in
various
fields
are
naturally
imbedded
in
a new
family
of
differential
equations.
Each
equation
belonging
to
that
family
can
be
brought
into
a
factorized
canonical
form
for
which
integrable
cases
can
be
identified
and
solutions
can
be
found
by
quadratures.
359

Recently,
Brenig
(1988]
has
developed
such
a
technique,
and
generalized
multi-dimensional
(multi-species)
Volterra
equations
are
used
as
examples
to
illustrate
the
power
of
such
an
approach.
(i)
The
effect
of
crowding
Let
us
introduce
a
term
representing
retardation
of
growth
due
to
crowding
in
the
predator-prey
problem
of
Votka-Volterra
equations
in
Section
1.1.
In
particular,
we
consider
the
equations
dN
1
/dt
= aN
1
-
bN
1
N
2
-
eN
1
2
(7.
5-1)
dN
2
jdt
=
-cN
2
+ dN
1
N
2
•
Again,
all
the
constants
a,
b,
c,
d,
e
are
positive.
One
equilibrium
point
is
N
1
= N
2
= o.
Another
one
is
N
1
=
aje,
N
2
= o,
corresponding
to
the
equilibrium
of
the
logistic
growth
of
the
prey
in
the
absence
of
predators.
Any
equilibrium
point
with
nonzero
values
of
both
N
1
and
N
2
must
satisfy:
a - bN
2
-
eN
1
=
0,
- c +
dN
1
=
0.
Thus
the
unique
equilibrium
solution
is
N
1
=
cjd,
N
2
=
(da
-
ec)/bd.
If
aje
>
cjd,
this
is
a
positive
equilibrium.
Applying
the
same
procedure
as
in
Section
1.1,
we
can
change
the
variables
x
1
= dN
1
jc,
x
2
=
bdN
2
/
(ad
-ce).
(7.
5-2)
Then
it
converts
Eq.(7.5-1)
to
dx
1
jdt
=
ax
1
(1
- x
2
)
+
px
1
(1
- x
1
),
dx
2
jdt
= -
cx
2
(1
-x
1
),
where
a = a -
cejd,
P =
ecjd.
For
x
1
>
0,
x
2
> o,
let
us
define
V(x
1
,x
2
)
=
cx
1
-
c
logx
1
+
ax
2
-
a
logx
2
•
It
has
a
minimum
at
the
equilibrium
point
(1,1).
Indeed,
we
find
that
dV(x
1
,x
2
)/dt
= - c
/3(1
- x
1
)
2
S o.
Thus,
V
is
a
Liapunov
function
of
the
system.
Using
Corollary
5.2.15,
one
can
show
that
(1,1)
is
asymptotically
stable
over
the
interior
of
the
positive
quadrant.
Hainzl
(1988]
studied
the
predator-prey
system
a
la
Bazykin
(1976]
whcih
depends
on
several
parameters,
360

including
the
stability
of
equilibria,
the
Hopf
bifurcation,
the
global
existence
of
limit
cycles,
the
global
attractivity
of
equilibria,
and
the
codimension
two
bifurcations.
Recently,
Hardin
et
al
[1988]
analyzed
a
discrete-time
model
of
populations
that
grow
and
disperse
in
separate
phases,
where
the
growth
phase
is
a
nonlinear
process
that
allows
for
the
effects
of
local
crowding,
while
the
dispersion
phase
is
a
linear
process
that
distributes
the
population
throughout
its
spatial
habitat.
The
issues
of
survival
and
extinction,
the
existence
and
stability
of
nontrivial
steady
states,
and
the
comparison
of
various
dispersion
strategies
are
discussed,
and
the
results
have
shown
that
all
of
these
issues
are
tied
to
the
global
nature
of
various
model
parameters.
Recently,
Tucker
and
Zimmerman
[1988]
have
studied
the
dynamics
of
a
population
in
which
each
individual
is
characterized
by
its
chronological
age
and
by
an
arbirary
finite
number
of
additional
structural
variables,
and
the
nonlinearities
are
introduced
by
assuming
that
the
birth
and
loss
processes,
as
well
as
the
maturation
rates
of
individuals,
are
controlled
by
a
functional
of
the
population
density.
The
model
is
a
generalization
of
the
classical
Sharpe-Lotka-McKendrick
model
of
age-structured
population
growth
[Sharpe
and
Lotka
1911,
McKendrick
1926],
the
nonlinear
age-structured
model
of
Gurtin
and
Maccamy
[1974],
and
the
age-size-structured
cell
population
model
of
Bell
and
Anderson
[1967].
Weinstock
and
Rorres
[1987]
investigated
the
local
stability
of
an
equilibrium
population
configuration
of
a
nonlinear,
continuous,
age-structured
model
with
fertility
and
mortality
dependent
on
total
population
size.
They
introduce
the
marginal
birth
and
death
rates,
which
measure
the
sensitivities
of
the
fertility
and
mortality
of
the
equilibrium
population
configuration
to
changes
in
population
size.
They
have
found
that
in
certain
cases
the
values
of
these
two
parameters
completely
determine
the
stability
classification.
361

(ii)
Autocatalytic
reaction:
Recently,
some
experimental
investigations
were
undertaken
in
studying
competition,
selection
and
permanence
in
biological
evaluation
and
molecular
systems
far
from
equilibrium.
Polynucleotides,
such
as
RNA
and
enzymes
of
simple
bacteria-
phages
are
used
in
these
experiments
[Biebricher
1983].
Polynucleotides,
strangely
enough,
have
an
intrinsic
capability
to
act
as
autocatalysts
built
into
their
molecular
structures.
A
combination
of
an
autocatalytic
reaction,
a
degradation
reaction
and
a
recycling
process
was
found
to
be
adequate
in
representing
an
appropriate
mechanism
for
modeling
such
system.
We
consider
the
open
system
A + X c••c
2X,
X
d'•d
B,
B
r<E>
....
A.
(7.
5-3)
The
rate
constant
of
the
recycling
reaction
r(E)
is
determined
by
an
external
energy
source
E.
A
simple
example
of
such
a
process
is
a
photochemical
reaction
using
a
light
source.
The
dynamics
of
the
mechanism
(7.5-3)
can
be
described
by
dajdt
rb
+
c•x•
-
cax,
(7.5-4a)
db/dt
=
dx
-
(d'
+
r)b,
(7.5-4b)
dxjdt
=
cax
+
d'b
-
c•x•
-
dx,
(7.5-4c)
where
we
denote
the
concentrations
of
A,
B
and
X
by
a,
b,
x
respectively.
A
trivial
constant
of
motion
is
the
total
concentration
of
all
substance,
i.e.,
a + b + x = c
0
=
constant.
(7.
5-5)
Thus
we
are
left
with
a
two-dimensional
system
defined
on
the
state
space:
s = (
(a,b,x)
€
R+
3
:
a + b + x = c
0
}.
Clearly
the
fixed
points
of
Eqs.(7.5-4)
are
P
0
(b
0
,x
0
)
=
(0,0),
(7.5-6a)
P
1
(b
1
,x
1
)
[cc
0
(d'+r)-dr]/[
(c+c')
(d'+r)+cd]
·
(d/
(d'+r),
1).
(7.5-6b)
If
C
0
<
ccrit
=
drj[c(d'+r)],
then
P
1
f
R+
3
,
i.e.,
outside
the
physically
relevant
state
space
S.
At
C
0
=
ccrit'
P
1
= P
0
and
enters
S
for
C
0
>
ccrit"
Local
stability
analysis
shows
that
362

P
1
is
asymptotically
stable
and
P
0
is
a
saddle
for
c
0
>
ccrit'
and
P
0
is
a
sink
for
C
0
<
ccrit.
In
order
to
find
qlobal
stability,
we
apply
the
Dulac-
function,
x·
1
,
to
the
vector
field,
Eqs.(7.5-4),
and
obtain:
x·
1
db/dt
=
(db/dt)
d -
(d'
+r)
bjx,
(7.
5-7
a)
x·
1
dx/dt
=
(dxjdt)
=
c(c
0
- b -
x)
+
d'b/x
-
c'x
-
d.
(7.5-7b)
These
equations
(or
vector
field),
Eqs.(7.5-7),
have
a
strictly
neqative
diverqence
on
s.
Thus
the
flow
(7.5-7)
is
area
contractinq,
consequently,
periodic
orbits
are
not
possible.
It
is
appropriate
to
recall
and
restate
the
famous
theorem
of
Poincare-Bendixson
(Theorem
4.3.1):
A
nonempty
compact
n-
or
a-
limit
set
of
a
planar
flow,
which
contains
no
fixed
points,
is
a
closed
orbit.
Thus,
the
Poincare-
Bendixson
theorem
implies
that
the
stable
stationary
solutions
P
0
or
P
1
are
indeed
qlobally
stable;
every
solution
startinq
in
s
converqes
to
the
stable
fixed
point.
If
the
deqradation
is
irreversible,
i.e.,
d'
= o,
qlobal
stability
of
P
1
can
also
be
proved
by
means
of
the
Liapunov
function:
v =
c(b
- b
1
)
• +
2d(x
- x
1
loq
x),
(7.
5-8)
where
(b
1
,x
1
)
are
the
coordinates
of
P
1
,
qiven
by
(7.5-6b).
The
autocatalytic
reaction
mechanism
described
by
(7.5-3)
admits
only
two
qualitatively
different
types
of
dynamical
behavior.
The
plane
of
external
parameters
(r,c
0
)
is
split
into
two
reqions
correspondinq
to
the
stability
of
either
P
0
or
P
1
(Fiq.
7.5.1)
d
c
Fiq.7.5.1
363
