Лазарев Ю.Ф. Mатематическое моделирование физических процессов и технических систем в MATLAB

Подождите немного. Документ загружается.

181

Исп

того

След

по з ее вхо роцеду

che

c является скаляром и не указан после него флажок 'high', то проектиру-

ользование функции

lp2bs

проектирования режекторного типа полностью аналогично, за исключением

, что параметры Wo и Bw в этом случае имеют смысл центра полосы задерживания и ее ширины.

ующую, четвертую группу образуют процедуры полной разработки фильтров указанных аппроксимаций

аданным порядку и значению частоты среза Wc. В н дят п ры

besself, butter, cheby1,

by2

и ellip. Общим для всех их является следующее:

- с их помощью можно проектировать ФНЧ, ФВЧ, полосовые и режекторный фильтры соответствующей

аппроксимации; если параметр W

ется

ФНЧ с частотой среза Wc; если же указанный флажок в обращении есть, то в результате проектирует-

ся

ФВЧ; если параметр Wc задан как вектор из двух величин, то результатом вычислений являются пара-

метры

полосового фильтра с полосой пропускания

21 WW ≤≤

, где W1 - первый элемент этого век-

конец, если дополн нце списка входных параметров ука-

ются параметры

режекторного

тора, а W2 -второй элемент; на ительно к этому в ко

зан "флажок" 'stop', то рассчитыва

фильтра с полосой задерживания, ука-

иметь три формы в зависимости от того, какое количество параметров

циента усиления фильтра; если же выходов указано четыре, то ими ста-

ектируемого фильтра;

цифровой форме не существует.

5.4.3. Проектирование БИХ-фильтров

(z), записанной в виде (5.7)

занной элементами вектора Wc

- результаты расчета фильтра могут

указано при обращении к процедуре в качестве выходных, например:

[b, a] = besself(n, Wc, 'ftype')

[z, p, k] = besself(n, Wc, 'ftype')

[A, B, C, D] = besself(n, Wc, 'ftype');

если указано два выходных параметра, то им будут присвоены значения коэффициентов числителя и

зна-

менателя передаточной функции фильтра; при указании трех параметров на выходе, они примут значения

векторов нулей, полюсов и коэффи

новятся значения матриц пространства состояний про

- почти все они могут применяться для проектирования как аналоговых, так и цифровых фильтров; чтобы

их помощью «создать» аналоговый фильтр необходимо в число входных параметров процедуры послед-

ним включить специальный «флажок» (

's'

); исключение составляет фильтр Бесселя, аналога которому

Конечной задачей проектирования линейного цифрового фильтра будем считать расчет значений элементов

векторов b числителя и a знаменателя его дискретной передаточной функции G

zbzbbzy

−−

⋅++⋅+ ...)(

zazaa

−−

⋅++⋅+

...

)(

Если эти два вектора известны, осуществление самой фильтрации, как было сказано ранее, про пр

нением процедуры

filter,

в которой аргументами выступают эти векторы.

)

исходит име-

Напомним, что представленная дискретная передаточная функция описывает в сжатой форме такое конечно-

разностное уравнение фильтра

)(...)1()(

)(...)2()1()(

mkxbkxbkxb

nkyakyakyakya

−⋅++−⋅+⋅=

=−⋅++−⋅+−⋅+⋅

(5.46

Если n=0, фильтр называют

нерекурсивным, а число m - порядком фильтра. Такой фильтр имеет конечную им

пульсную характеристику, поэтому его также называют КИХ-фильтром.

В случае

0>n

фильтр называется

рекурсивным. Порядком фильтра при этом называют наибольшее из чисел

m и n. В этом случае импульсная характеристика фильтра является бесконечной, и последний называют также

БИХ-фильтров. БИХ-фильтры представляют собой некоторые аналоги динамических звеньев.

Одним из средств проектирования БИХ-фильтров, предус

соответствующего аналогового прототипа, т. е. нахождение

передаточной функции по Лапласу непрерывного

ру п ного

не ь. Би-

еобразование выполняется в соответствии с выражением

мотренных в пакете SIGNAL, является разработка

фильтра, и последующий переход к цифровому фильт утем нахождения цифрового аналога непрерыв

звена. Последнее можно осуществить с помощью били йного преобразования s-плоскости в z-плоскост

линейное пр

)()(

−

sHzH

, (5.47

)

182

где f

- частота дискретизации сигн ничную окружность на z-

плоскости.

В пакете SIGNAL билине

ilinear, которая име-

d] = bilinear(A, B, C, D, Fs, Fp).

мов числителя и знаменателя дис-

тного пространства состояний

фильтра по известным матрицам неп

ала. При этом ось

преобразуется в еди

йное преобразование осуществляется с помощью процедуры

ет три формы обращения к ней:

[bd, ad] = bilinear(b, a, Fs, Fp)

[zd, pd, kd] = bilinear(z, p, k, Fs, Fp)

[Ad, Bd, Cd, D

Все они преобразуют параметры, характеризующие аналоговый прототип фильтра, в аналогичные параметры

описывающие дискретный БИХ-фильтр. Вид и количество входных параметров определяют вид и число вы-

ходных. Параметр Fs задает частоту дискретизации в герцах. Последний параметр Fp не обязателен. Он опреде

ляет частоту в герцах, для которой значения АЧХ до и после выполнения преобразования

должны совпадать, т

е. задает так называемые предыскажения.

Обращение в первой форме позволяет определить коэффициенты полино

кретной передаточной функции фильтра вида (5.35) по заданным коэффициентам полиномов числителя и зна-

менателя непрерывной передаточной функции вида (5.34). Обращение во второй форме дает возможность вы-

числить нули, полюсы и коэффициент усиления

дискретного фильтра по заданным аналогичным параметрам

аналогового прототипа. И, наконец, третья форма определяет матрицы дискре

рерывного пространства состояний.

Второй способ построения цифрового фильтра по его аналоговому прототипу заключается в таком преобразо-

вании параметров аналогового фильтра в параметры дискретного фильтра, при котором импульсная характери

стика

последнего совпадала бы с импульсной характеристикой аналогового фильтра в точках через дискрет по

времени. Это в MatLAB осуществляется применением процедуры

impinvar:

[bz, az] = impinvar(b, a, Fs).

Здесь b и a - заданные векторы коэффициентов числителя и знаменателя передаточной функции аналогового

прототипа фильтра, bz и az - вычисляемые коэффициенты числителя и знаменателя дискретной передаточной

функции дискретного фильтра, Fs - заданная частота дискретизации сигнала в герцах. Если параметр Fs при

обращении не указан, то по умолчанию он принимается равным 1 Гц.

Третий способ формирования дискретных фильтров - использование ранее рассмотренных

процедур формиро

вания фильтров

butter, cheby1, cheby2 и ellip. Если при обращении к этим процедурам не указывать в

ся в другом пред-

должны задаваться по отношению к так называе-

конце списка входных параметров «флажка»

's', то результатом работы этих процедур будут параметры

именно цифровых фильтров.

Основное отличие применения этих функций для разработки цифровых фильтров заключает

ставлении задаваемых частот в векторе Wc.

Все частоты

мой "частоте Найквиста". Частотой Найквиста называют половину частоты дискретизации сигнала.

Так как диапазон частот изменения дискретного сигнала всегда меньше частоты дискретизации, то все частот-

ные характеристики дискретных фильтров определяются только внутри диапазона от 0 до частоты Найквиста.

граничные частоты должны быть меньше единицы.

ИХ-фильтров.

енного цифрового фильтра Баттерворта. Формы обращения к

= maxflat(nb,na, Wc)

метричного КИХ-фильтра Баттервор-

Поэтому все задаваемые в векторе Wc

Существуют еще две процедуры расчета Б

Процедура

maxflat производит расчет обобщ

ней таковы:

[ b, a] = maxflat(nb, na, Wc)

[ b, a] = maxflat(nb, 'sym', Wc)

[ b, a, b1, b2]

[ b, a] = maxflat(nb,na, Wc, 'design_flag').

Первое обращение позволяет вычислить коэффициенты b - числителя и а -знаменателя дискретной передаточ-

ной функции H(z) цифрового ФНЧ Баттерворта с частотой среза Wc, порядок числителя которой равен nb, а

знаменателя - na.

При обращении второго вида вычисляются коэффициенты цифрового сим

та. В этом случае na принимается равным 0. Параметр nb должен быть четным.

Если обратиться к процедуре так

, как указано в третьем обращении, т. е. указать в качестве выходных четыре

величины, то дополнительные параметры b1 и b2 определят коэффициенты двух полиномов, произведение ко-

183

торых яв даточной функции, причем все нули полино-

ма , а полином b2 содержит все остальные нули полинома b.

Доб ение в список входных параметров процедуры параметра

'design_flag' позволяет изменять харак-

тер вно

'trace', на экране отображаются

пар тры, используемые в процессе проектирования:

>> nb=10; na = 2; w = 0.6;

flat(nb,na,w,'trace')

5 2 0.53312

6 2 0.6009

7 2 0.67409

8 2 0.76062

9 0.54459

Есл то на экран будут выведены графики амплитудной харак-

тер ажение нулей и полюсов:

ляется полиномом числителя b искомой дискретной пере

b1 равны -1

авл

выводимой на экран информации. Если значение этого параметра ра

аме

>> [b,a,b1,b2] = max

Table:

L M N wo_min/pi wo_max/pi

Columns 1 through 4

10 0 2 0

9 1 2 0.23938

8 2 2 0.32591

7 3 2 0.3991

4 2 0.46688 6

Column 5

0.23938

0.32591

0.3991

0.46688

0.53312

0.6009

0.67409

0.76062

b =

0.11478 0.50222 0.8130

0.070336 -0.052259 0.0040606 0.0050236

3.2299e-005 -0.0022396 0.00042191 -

a = 1 0.46247 0.53752

b1 = 1 5 10 10 5 1

0.11478 -0.071679 0.023681 -0.0048336

0.0005834 -3.2299e-005

и же этому параметру задать значение 'plots',

истики, группового времени замедления, а также графическое изобр

>>[b,a,b1,b2] = maxflat(nb,na,w,'plots')

184

b = 0.11478 0.50222 0.81309 0.54459

0.070336 -0.052259 0.0040606 0.0050236

-0.0022396 0.00042191 -3.2299e-005

a = 1 0.46247 0.53752

b1 = 1 5 10 10 5 1

b2 = 0.11478 -0.071679 0.023681 -0.0048336

0.0005834 -3.2299e-005

Рис. 5. 44. Результат выполнения процедуры MAXFLAT(nb,na,w,'plots')

Расчет БИХ-фильтра по заданной амплитудно-частотной характеристике производится процедурой

yulewalk

. Если набрать в командном окне MatLAB строку

[ b, a] = yulewalk(n, f, m),

то будут ретной передаточной функции БИХ-

фильтра ванных значениях) и m - соответст-

вующих ектора f должен быть равен 0, а по-

следний м порядке. Частоты, при которых

происхо твующих им «амплитуд».

Приведем пример расчета ФНЧ 8-го порядка и построим желаемую АЧХ и АЧХ полученного фильтра. Резуль-

тат приведен на рис. 5.45.

f = [ 0 0.5 0.5 1]; m=[1 1 0 0];

[b,a] = yulewalk(8,f,m); [h,w] = freqz(b,a, 128);

plot(f,m, w/pi,abs(h))

set(gca,'FontSize',12)

grid, title('Пример применения процедуры YULEWALK')

xlabel('Нормализованная частота'), ylabel('А Ч Х')

вычислены коэффициенты b - числителя и a - знаменателя диск

ана векторами f (частоты в нормиро порядка n, АЧХ которого зад

значений отношений амплитуд выхода и входа. Первый элемент в

1. Все остальные элементы должны быть расположены в неубывающе

дит скачок АЧХ, указываются два раза с разными значениями соответс

185

Рис. 5. 45. Пример применения процедуры YULEWALK

ором b.

ункции тождественно равен 1.

фа-

ения которых определяют границы полосы задерживания по отно-

ьтра, первая

числом.

Параметр n+1. Если этот параметр

не указан

Для вычи кции:

кна;

, где r - желаемый уровень

kaizer(n, beta) - создает вектор-столбец и элементов окна Кайзера, где параметр beta опреде-

ляет затухание боковых лепестков преобразования Фурье окна;

triang(n) - создает вектор-столбец из n элементов треугольного окна.

5.4.4. Проектирование КИХ-фильтров

В отличие от БИХ-фильтров, которые характеризуются двумя векторами - коэффициентов b числителя и а -

знаменателя своей дискретной передаточной функции, КИХ-фильтры описываются только одним вект

Знаменатель их дискретной передаточной ф

Группа функций

fir1

предназначена для расчета коэффициентов b цифрового КИХ-фильтра с линейной

зой методом взвешивания с использованием окна. Общий вид обращения к этой процедуре имеет вид

b = fir1(n, Wn, 'ftype', window).

Процедура вычисляет вектор n+1 коэффициентов b КИХ-фильтра с нормализованной частотой среза Wn.

Параметр

'ftype' задает желаемый тип фильтра (ФНЧ, ФВЧ, полосовой или режекторный). Он может от-

сутствовать - и тогда по умолчанию рассчитываются параметры ФНЧ c частотой среза Wn, если последняя за-

дана как скаляр, или полосовой фильтр с полосой пропускания от W1 до W2, если Wn задан в виде вектора из

двух элементов [W1 W2], - или принимать одно из четырех значений :

'high', 'stop', 'DC-1' и 'DC-0'. В

первом случае синтезируется ФВЧ с частотой среза Wn. Во втором, - режекторный фильтр (при этом Wn дол-

жен быть вектором из двух элементов, знач

шению к частоте Найквиста). В третьем случае рассчитываются параметры многополосового фил

полоса которого является полосой пропускания, а в четвертом, - тоже

многополосовый фильтр, первая полоса

которого является полосой задерживания.

При расчете режекторных фильтров и ФВЧ порядок фильтра следует назначать четным

window позволяет задавать отсчеты окна в векторе-столбце window длины

, то, по умолчанию, будет использовано окно Хемминга.

сления окон различного типа в MatLAB предусмотрены следующие фун

bartlett(n) - создает вектор-столбец из n элементов окна Бартлетта;

blackman(n) - создает вектор-столбец из n элементов окна Блекмана;

boxcar(n) - создает вектор-столбец из n элементов прямоугольного о

chebwin(n,r) - создает вектор-столбец из n элементов окна Чебышева

допустимых пульсаций в полосе задерживания в децибелах;

hamming(n) - создает вектор-столбец из n элементов окна Хэмминга;

hanning(n) - создает вектор-столбец из n элементов окна Хэннинга;

з n

186

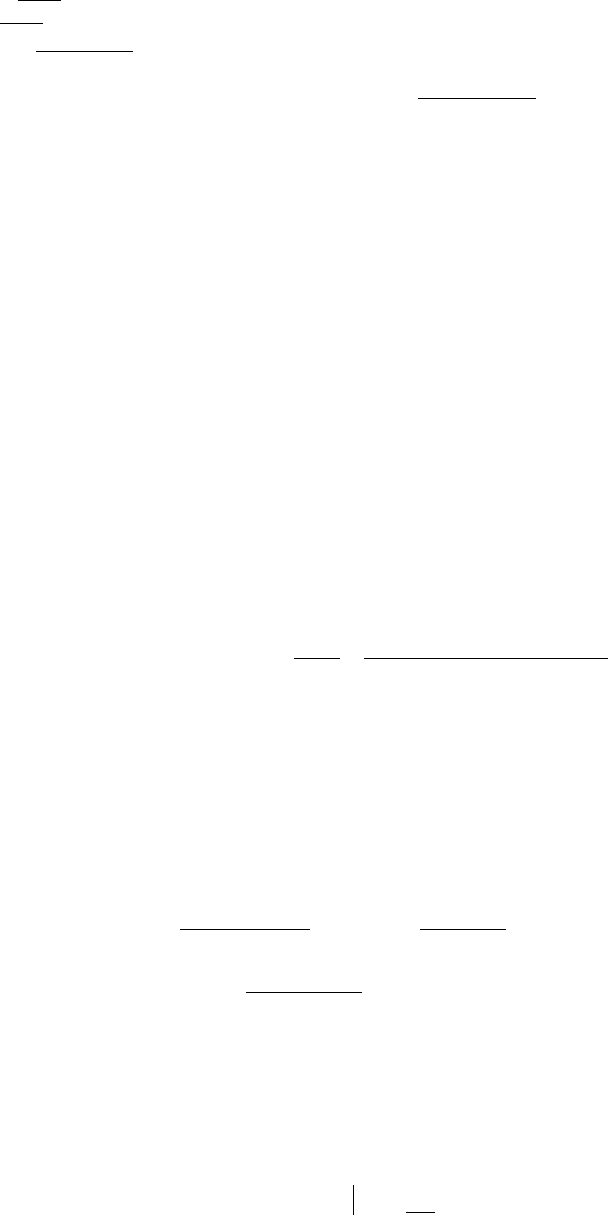
Рис. 5. 46. Результат применения процедуры FIR1

Приведе сового КИХ-фильтра 24 порядка с полосой пропускания

≤

оэффициентов цифрового КИХ-фильтра с произвольной ампли-

векторами f частот и m - соответствующих желаемых значений

орым выполняется интерполяция АЧХ. Параметр lap опреде-

разного изменения АЧХ

, в которой выполняется сгла-

живание чанию, принимается npt = 512 и lap = 25.

Рассчит порядка:

xlabel('Нормализованная частота'), ylabel('А Ч Х')

На рис. 5.47 приведены желаемая АЧХ и АЧХ, полученная в результате расчета.

м пример. Произведем расчет поло

35.0 65.0/ ≤

ωω

b = fir1(48,[0.35 0.65]);

freqz(b,1,512)

set(gca,'FontSize',12)

title('Результат применения процедуры FIR1')

Результат показан на рис.5.46.

Группа процедур

fir2 служит для расчета к

тудно-частотной характеристикой, задаваемой

АЧХ. Общий вид обращения к процедуре таков:

b = fir2(n, f, m, npt,lap, window).

Вектор f должен содержать значения нормализованной частоты в неубывающем порядке от 0 до 1. Вектор m

должен быть той же длины, что и вектор f, и содержать желаемые значения АЧХ на соответствующих часто-

тах.

Параметр npt позволяет задать число точек, по кот

ляет размер (число точек) области около точек скачкооб

, по умол. Если эти параметры не указаны, то

аем двухполосный фильтр 30-го

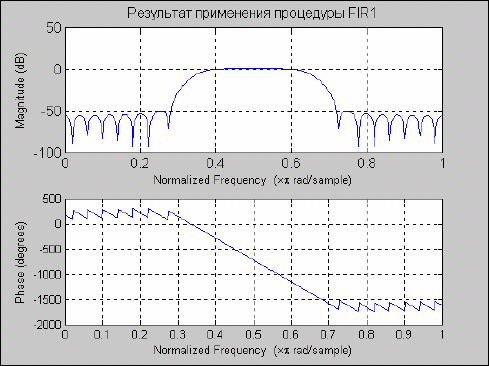
f = [0 0.2 0.2 0.6 0.6 0.8 0.8 1];

0]; m = [ 1 1 0 0 0.5 0.5 0

b = fir2(30,f,m);

[h,w] = freqz(b,1,512);

plot(f,m,w/pi,abs(h)), grid

set(gca,'FontSize',12)

title('АЧХ КИХ-фильтра (процедура FIR2)')

- также рассчитывает многополосный фильтр, но в несколько другой форме -

Рис. 5. 47. АЧХ КИХ-фильтра (процедура FIR2)

Следующая процедура -

fircls

путем задания кусочно-постоянной желаемой АЧХ.

Формат обращения к ней таков

b = fircls(n, f, amp, up, lo, 'design_flag').

187

Здесь f, как и ранее, вектор значений нормализованных частот (от 0 до 1), определяющих границы полос

фильтра. Вектор amp определяет кусочно-постоянную желаемую АЧХ фильтра, количество его элементов рав-

элементов вектора f. Векторы up и lo определя-

АЧХ спроектированного фильтра от желаемой

для

Пар

ржки, нулей и полюсов;

bot ме.

Приведе о фильтра:

]; amp = [1 0 0.5 0];

Рез

-0.014469

-6.0306e-005 0.0089569 -0.062583 -0.023061

-0.010522 0.001063 0.0059551 0.010051

0.022633 -0.0030717 -7.4344e-005

но числу полос фильтра и, следовательно, на 1 меньше числа

ют соответственно верхние и нижние допустимые отклонения

каждой из полос. Размер их совпадает с размером вектора amp.

аметр

'design_flag' может принимать три значения:

trace - для обеспечения вывода результатов в виде текстовой таблицы;

plots - для графического отображения АЧХ, групповой заде

h - для отображения результатов как в текстовой, так и в графической фор

м пример разработки прежнего двухполосног

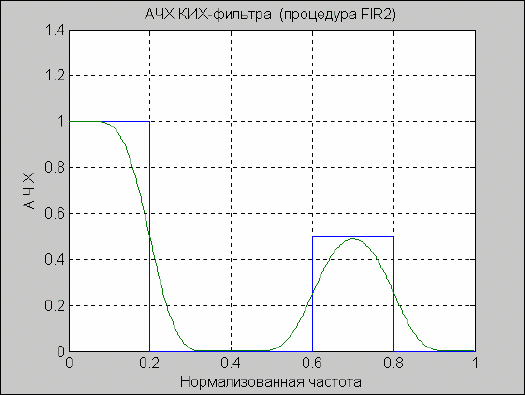
n= 30; f = [0 0.2 0.6 0.8 1

up = [1.02 0.02 0.51 0.02];lo = [0.98 -0.02 0.49 -0.02 ];

b = fircls(n,f,amp,up,lo,'both')

ультат приведен ниже и на рис. 5.50.

Bound Violation = 0.0755112846369

Bound Violation = 0.0116144793011

Bound Violation = 0.0004154355279

Bound Violation = 0.0000905996658

Bound Violation = 0.0000214272508

Bound Violation = 0.0000009624286

Bound Violation = 0.0000002393147

Bound Violation = 0.0000000596813

Bound Violation = 0.0000000146532

Bound Violation = 0.0000000036610

b =

-7.4344e-005 -0.0030717 0.022633 0.010051

0.0059551 0.001063 -0.010522 -0.023061

-0.062583 0.0089569 -6.0306e-005 -0.014469

0.17747 0.11938 0.12718 0.3023

0.12718 0.11938 0.17747

Для срав едуры

fir2 построим график полученной АЧХ, аналогичный при-

веденно

Рис. 5. 48. Результат применения процедуры FIRCLS

нения с результатами работы проц

му на рис. 5.47:

[h,w] = freqz(b,1,512);

188

plot(w/pi,abs(h)), grid

set(gca,'FontSize',12)

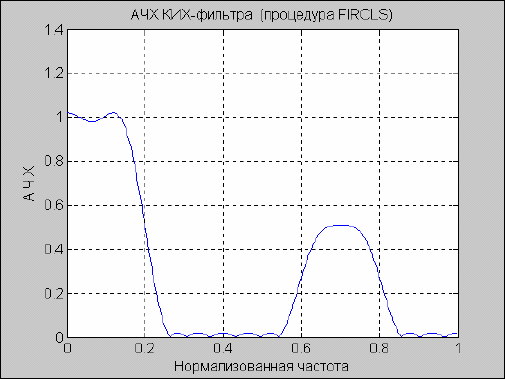
title('АЧХ КИХ-фильтра (процедура FIRСLS)')

xlabel('Нормализованная частота'), ylabel('А Ч Х')

Результат представлен на рис. 5.49.

Рис. 5. 49. АЧХ КИХ-фильтра (процедура FIRСLS)

я расчета параметров ФНЧ и ФВЧ с КИХ методом наименьших

АЧХ. Предусмотрены следующие виды обращения к этой проце-

итанного фильтра от 1 в полосе пропускания, а ds - максимальное отклонение АЧХ рас-

Если этот флажок отсутствует,

торой при Wt <

коэффициентов цифрового КИХ-фильтра с линейной ФЧХ по

использован обменный алгоритм Ремеза и метод аппроксимации Че-

т-

Процедура

предназначает fircls1 ся дл

квадратов с учетом допусков на отклонения

дуре:

b =fircls1(n, Wo, dp, ds)

b =fircls1(n, Wo, dp, ds, 'high')

b =fircls1(n, Wo, dp, ds, Wt)

b =fircls1(n, Wo, dp, ds, Wt, 'high')

b =fircls1(n, Wo, dp, ds, Wp, Ws, k)

b =fircls1(n, Wo, dp, ds, Wp, Ws, k, 'high')

b =fircls1(n, Wo, dp, ds, . . ., 'design_flag').

Параметр Wo представляет собой нормализованную частоту среза; dp определяет максимально допустимое

отклонение АЧХ рассч

считанного фильтра от 0 в полосе задерживания.

Наличие флажка

'high' определяет, что рассчитываются параметры ФВЧ.

рассчитывается ФНЧ.

Указание параметра Wt позволяет задать частоту Wt, выше которой при Wt > Wo или ниже ко

Wo гарантируется выполнение требований к АЧХ синтезируемого фильтра.

Параметры Wp, Ws и k позволяют соответственно задать граничную частоту пропускания, граничную частоту

задерживания и отношение ошибки в полосе пропускания к ошибке в

полосе задерживания.

Флаг

'design_flag' имеет тот же смысл и принимает те же значения, что и у предыдущей процедуры.

Группа процедур

remez осуществляет расчет

алгоритму Паркса-МакКлелла, в котором

бышева. При этом минимизируется максимальное отклонение АЧХ спроектированного фильтра от желаемой

АЧХ. Приведем наиболее полный вид обращения к процедуре:

b = remez(n, f, а, W, 'ftype').

Вектор f должен состоять из последовательных, записанных в возрастающем порядке пар нормализованных (от

0 до 1) частот, определяющих соответственно нижнюю и верхнюю границы диапазона полосы пропускания

или задерживания. Вектор 'a' должен содержать желаемые значения АЧХ на частотах, определяемых соотве

189

ствующими элементами вектора

. Желаемая АЧХ в полосе частот от f(k) до f(k+1) при k нечетном представ-

ляет собой отрезок прямой от точки f(k), a(k) до точки f(k+1), a(k+1). В диапазонах от f(k) до f(k+1) при k - чет-

о из полос АЧХ, заданных парами частот вектора f. Эти

и определяют достигаемое при аппроксимации соотно-

шение ме

но полови нтов вектора f.

Флаг 'ftyp

льных методов взвешивания;

бки аппроксимации на низ-

пропорциональна часто-

Ниже пр 7-го порядка:

];

), grid

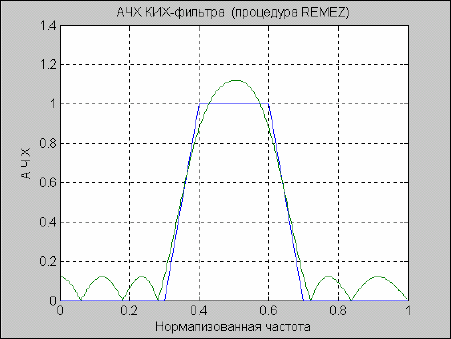
title('АЧХ КИХ-фильтра (процедура REMEZ)')

xlabel('Нормализованная частота'), ylabel('А Ч Х')

Результат приведен на рис.5.50.

ном значение желаемой АЧХ не определено (а, значит, при проектировании фильтра АЧХ в этих диапазонах

может принимать любое значение). Следует заметить, что f(1) должно всегда быть равным 0.

Векторы f и a

должны быть одинаковой длины, причем общее количество элементов каждого вектора должно быть четным

числом.

Вектор W задает значения коэффициентов веса каждог

коэффициенты используются при аппроксимации АЧХ

жду реальным и желаемым значением АЧХ в каждом из

диапазонов. Число элементов вектора W рав-

не числа элеме

e' может принимать одно из двух значений:

'hilbert' - в этом случае процедура проектирует фильтры с нечетной симметрией и линейной фа-

зой;

'differentiator' - синтезируется фильтр с использованием специа

са, про орциопри этом для ошибок задаются ве п нальные 1/f; поэтому оши

оров, АЧХ которыхких частотах меньше, чем на высоких; для дифференциат

тельная ошибкате, минимизируется максимальная относи

иводится пример проектирования полосового фильтра 1

f = [0 0.3 0.4 0.6 0.7 1]; a = [0 0 1 1 0 0

b = remez(17,f,a); [h, w] = freqz(b, 1, 512);

plot(f,a,w/pi,abs(h)

set(gca,'FontSize',12)

сremez

является то, что исходные данные по желаемой форме АЧХ

словно обозначенной fresp. Формы обращения к этой процедуре приведе-

)

, w)

p1,p2,...},w)

Рис. 5. 50. АЧХ КИХ-фильтра (процедура REMEZ)

Особенностью следующей процедур

фильтра задаются в виде функции, у

ны ниже:

b = cremez(n, f, 'fresp'

b = cremez(n, f, {'fresp',

b = cremez(n, f, a, w)

b = cremez(..., 'sym')

b = cremez(..., 'debug')

b = cremez(..., 'skip_stage2')

[b, delta, opt] = cremez(...).

190

Параметры n, f имеют тот же смысл и требования к их представлению такие же, как и при применении проце-

дуры

вект

Фун

кции

'fresp' не указаны дополни-

ри

ором

f; при этом вектор a указывается в качестве первого дополни-

ьтра с линейной фазой; при обращении к этой функции в качестве дополнительного парамет-

Fs=1;

чае находятся коэффициенты фильтра Гильберта с линейной

b =

Пар а. Он может при-

ним

по умолча-

е значение параметра исполь-

овых и режекторных фильтров;

выполняются оба этапа оптимизации. Параметр

'debug' (см.

Исп

бращения к процедуре) дает

возм итуды пульсаций АЧХ.

Вых

ции;

е opt.grid;

- o и

На рис. для расчета параметров полосового КИХ-

фильтра

= cremez(30,[0 0.5 0.6 0.8 0.9 1],'bandpass'); freqz(b,1,512)

set(gca,'FontSize',12)

title('АЧХ КИХ-фильтра (процедура СREMEZ)')

remez. В отличие от последней, вектор значений желаемой АЧХ, соответствующих заданным значения

ора f, определяется путем обращения к функции fresp.

кция

fresp может принимать одно из следующих: значений

- lowpass, highpass, bandpass, bandstop (ФНЧ, ФВЧ, полосовой и режекторный фильтры); при

этом рассчитываются параметры указанного типа фильтра; если к фун

тельные параметры (обращения к процедуре первого и второго видов), то групповое время замедления

(ГВЗ) принимается равным n/2; в случае же обращения к процедуре в третьей форме, где в качестве допол

нительного параметра функции

fresp указан один - d, ГВЗ = n/2+d;

- multiband (многополосовой фильтр); синтезируется фильтр, заданный вектором a желаемой АЧХ п

значениях частот, определенных вект

тельного параметра к функции multiband (третья форма обращения); если, кроме этого вектора, не указаны

другие дополнительные параметры, то ГВЗ принимается равным n/2, если же указан еще один дополни-

тельный параметр d, то ГВЗ = n/2+d;

- differentiator (дифференциатор); эта функция позволяет рассчитывать коэффициенты дифференци-

рующего фил

ра необходимо указать частоту дискретизации Fs; по умолчанию

- hilbfilt

(фильтр Гильберта); в этом слу

фазой.

Обращение к процедуре четвертого вида эквивалентно обращению

cremez(n, f, {'multiband', a},w).

аметр 'sym' позволяет задать тип симметрии импульсной характеристики (ИХ) фильтр

ать следующие значения:

- none - в этом случае ИХ может быть произвольной; это значение параметра используется

нию, если при определении желаемой АЧХ задаются отрицательные значения частот;

- even

- АЧХ должна быть вещественной с четным типом симметрии; тако

зуется по умолчанию при проектировании ФНЧ, ФВЧ, полос

- odd - АЧХ должна быть вещественной с нечетным типом симметрии; такое значение по умолчанию ис-

пользуется при проектировании фильтров Гильберта и дифференциаторов;

- real - АЧХ должна иметь сопряженный тип симметрии.

Использование флага

'skip_stage2'

(см. седьмой вид обращения к процедуре) позволяет не выполнять вто-

рой этап алгоритма оптимизации, который рассчитывает коэффициенты фильтра в тех случаях, когда этого

нельзя сделать с помощью алгоритма Ремеза. Исключение второго этапа сокращает время расчетов, но может

повлечь снижение точности. По умолчанию

шестой вид вызова процедуры) определяет вид выводимых на екран результатов расчета фильтра и может при-

нимать следующие значения:

'trace', 'plots', 'both'

'off'

. По умолчанию используется

'of

(т. е. на экран не выводится информация).

ользование дополнительного выходного параметра

delta (см. восьмой вид о

ожность использовать в дальнейших операциях значение максимальной ампл

одной параметр

opt содержит набор дополнительных характеристик:

- opt.grid - вектор отсчетов частоты, использованных при оптимиза

- opt.H - вектор значений АЧХ, соответствующих значениям элементов в вектор

- opt.error - вектор значений ошибок на частотах вектора opt.grid;

pt.fextr - вектор, содержащий частоты с экстремальными ош бками АЧХ.

5.53 изображен результат применения процедуры cremez

-го порядка. 30