Lawson M.V. Finite Automata

Подождите немного. Документ загружается.

< previous page page_127 next page >

Page 127

Chapter 6

Local languages

In Chapter 5, we showed how to construct an

-automaton A from a regular expression

. To complete

this process, and find a deterministic automaton recognising

L(r),

we need to convert A into a non-

deterministic automaton and then apply the accessible subset construction. The main aim of this chapter

is to show how to construct a non-deterministic automaton directly from the regular expression

6.1 Myhill graphs

In this section, we are going to focus on a simple-looking class of recognisable languages. We begin

with an example.

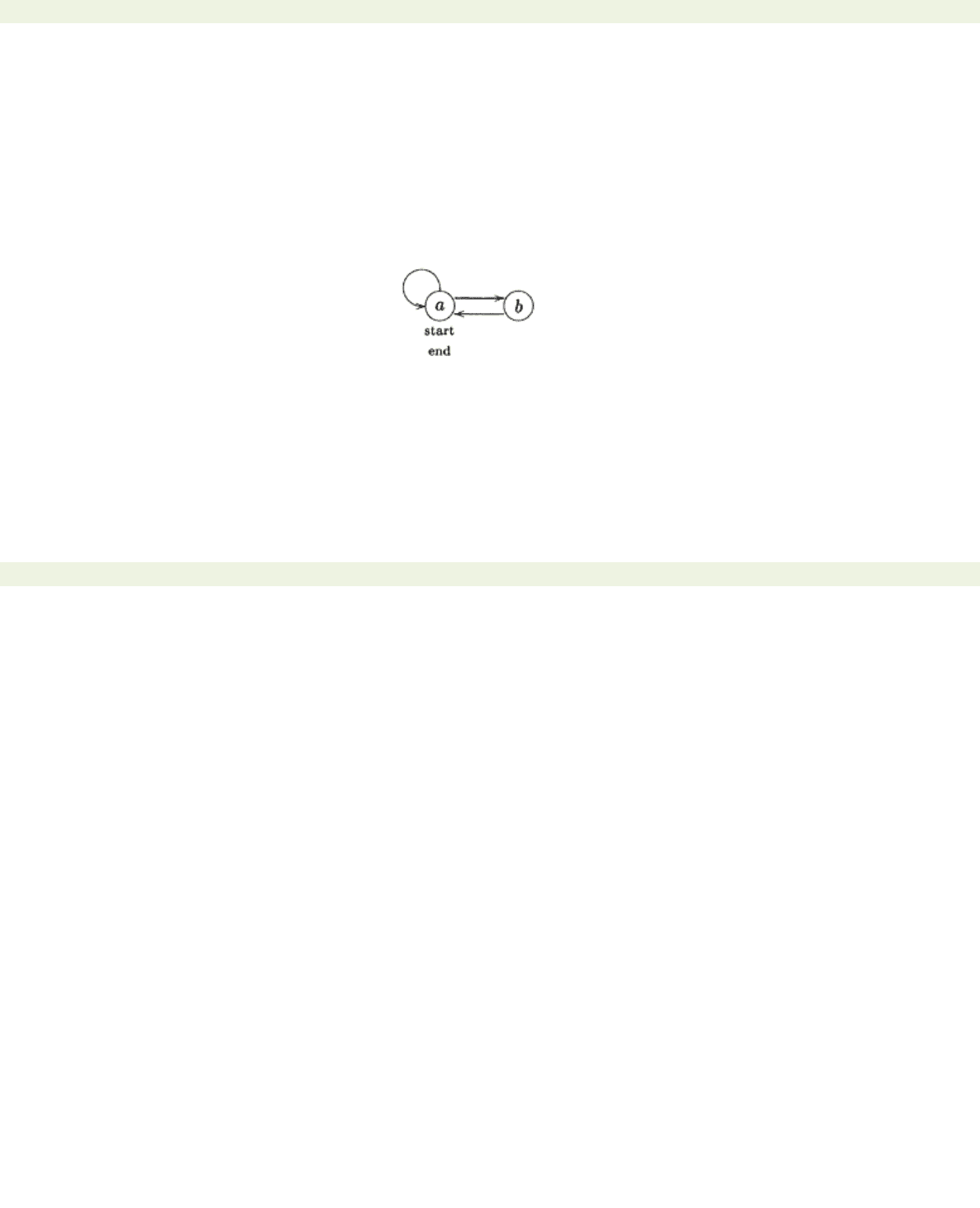
Example 6.1.1 Consider the following directed graph:

This is not an automaton, because there are no labels on the edges. However, this graph can still be

used to recognise strings over the alphabet

{a, b}

. The reason is that each

non-empty

string over

labels at most one path in this graph beginning at the vertex labelled ‘start’ and ending at the vertex

labelled ‘end.’ Specifically, the string

labels the unique path of length 0 starting and ending at the

vertex

the string

…an,

where

≥2, labels a path beginning at

and if for each pair

aiai

+1, where 1≤

≤

−1, there is an edge from

+1. By definition, the language recognised by

this graph consists of those non-empty strings that label a path beginning at

and ending at

. We can

explicitly describe this language. Observe that strings containing consecutive

’s cannot be recognised,

because there is no loop at

< previous page page_127 next page >

< previous page page_128 next page >

Page 128

the vertex

. It is now easy to see that the language recognised by this graph is

(aA

The graph in our example is an instance of the following. A

Myhill graph

(over the alphabet A)

is a

directed graph satisfying the following three conditions:

(MG1)For each ordered pair of vertices

1 and

2 there is at most one edge from

1 to

(MG2)Some vertices are designated

start vertices,

and some vertices are designated

end vertices

. A

vertex may be both a start and an end vertex.

(MG3)Each vertex is labelled with a different symbol from a finite alphabet

. This means that we can

refer to a vertex unambiguously by its label.

Let G be a Myhill graph over the alphabet

. An individual letter of

is said to be

allowable

if it labels a

vertex that is both a start and an end vertex. A non-empty string

,…, an

over

of length at least two

is said to be

allowable

1 labels a start vertex,

labels an end vertex, and for each 1≤

≤

−1 there

is an edge in G joining the vertex

to the vertex

+1. The

language, L

(G),

recognised

by a Myhill

graph G consists of all allowable strings in

Myhill graphs provide a simple way of describing languages, and we would obviously like to characterise

what these languages are. The first step in answering this question is to show that the language

recognised by a Myhill graph is recognisable. To do this, we shall prove that Myhill graphs can be

converted into special kinds of automata. We first indicate how this can be done with Example 6.1.1.

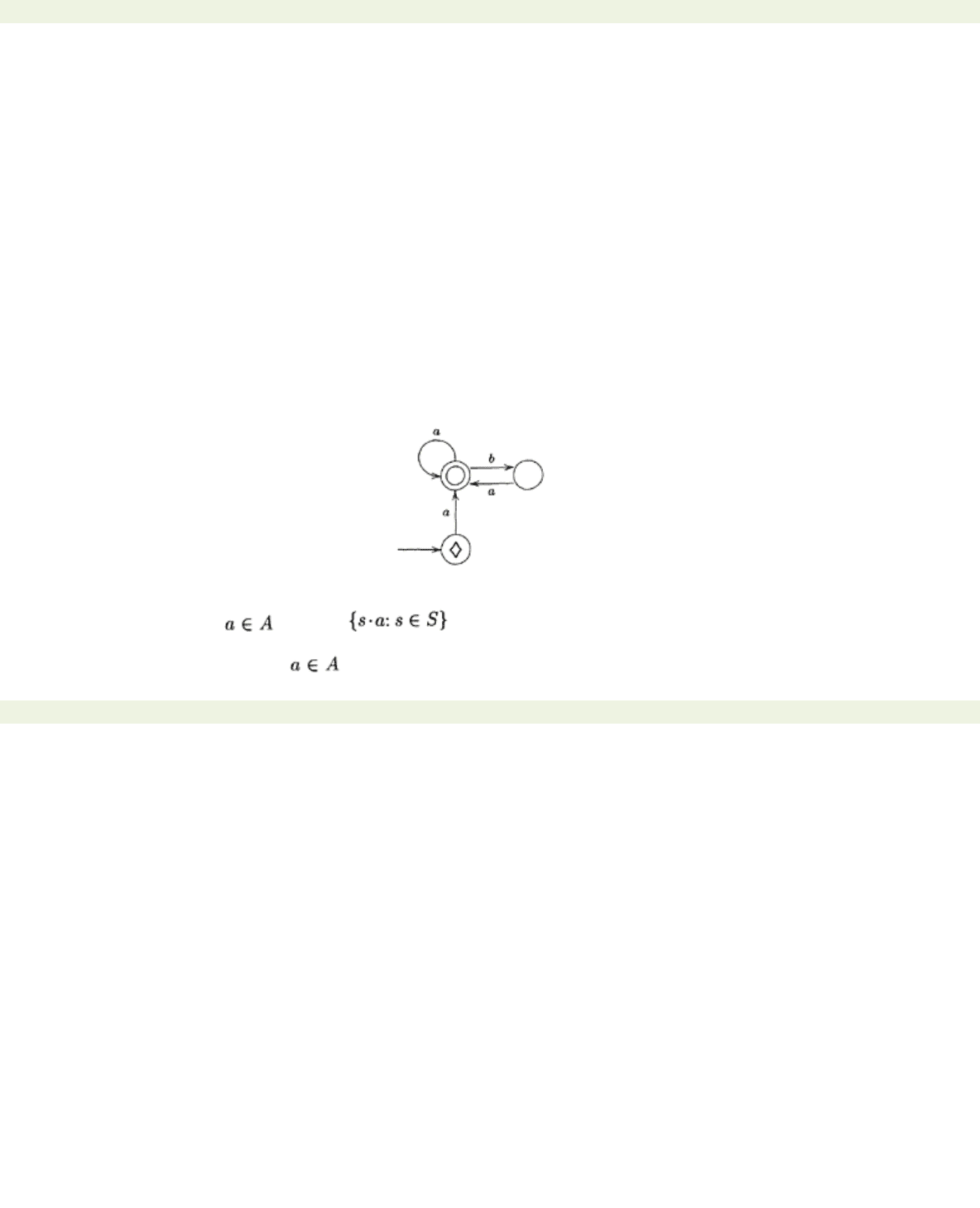
Example 6.1.2 Consider the following deterministic but incomplete automaton:

It is easy to check that it recognises the same language as Example 6.1.1.

Let A=

(S, A, i, δ, T)

be a deterministic automaton not necessarily complete. We say that A is a

local

automaton

if for each the set contains at most one element; we say that it is a

standard local automaton

if, in addition, there is no transition arriving at the initial state. Thus an

automaton is local if for each

either there are no transitions labelled by

< previous page page_128 next page >

< previous page page_129 next page >

Page 129

or if there are they all arrive at the same state. We show that Myhill graphs can be converted into

standard local automata and vice versa in such a way that languages are not changed.

Theorem 6.1.3

A language can be recognised by a Myhill graph if and only if it can be recognised by a

standard local automaton whose initial state is not terminal.

Proof Let G be a Myhill graph. We construct an automaton A as follows. Adjoin an extra vertex ◊ to G

with arrows from ◊ to each of the start vertices of G; label ◊ as the initial state; label the end vertices

as terminal states; label each arrow of the resulting directed graph with the symbol labelling the vertex

to which it points. Thus

is replaced by

It is clear that every transition is labelled. Call the resulting machine A. By construction, the initial state

is not terminal. I claim that A is deterministic. First the arrows emerging from the initial state are all

differently labelled because they point to states that were originally differently labelled by (MG3). If we

now consider any other state

then two transitions emerging from

could only have the same label if

in G both arrows pointed to the same vertex. However, this cannot occur by (MG1). Thus A is a

deterministic automaton, possibly incomplete. By construction it is both standard and local. It is now

easy to check that

(A)=

(G).

To prove the converse, let A=

(S, A, i, δ, T)

be a standard local automaton whose initial state is not

terminal. We construct a Myhill graph G as follows. First, label all states of A, except the initial state,

with the input symbol of all transitions that enter that state. This is well-defined from the definition of

‘local.’ Erase all labels on directed edges. Next, mark all states

as start vertices for which there are

transitions from

and mark all terminal states as end vertices. Finally, erase the vertex

and all

arrows that leave it. Call the resulting graph G. It is straightforward to check that G is a Myhill graph

and that

(G)=

(A).

We shall now describe the languages recognised by standard local automata. A language

is said

to be a

local language

can be described in the following way: there are subsets and

such that

This definition simply says that a local language is one in which determining whether a non-empty string

belongs to it boils down to some very elementary checks:

< previous page page_129 next page >

< previous page page_130 next page >

Page 130

• Check that the string begins with a letter from

• Check that no consecutive pair of letters in the string belongs to the set

of ‘forbidden factors.’

• Check that the string ends with a letter from

Thus to determine whether a string belongs to a local language it is enough to scan the string from left

to right through a window two-letters long; this is the meaning of the word ‘local.’ The set

is equal to

where

is the set of all factors of length 2 in the language

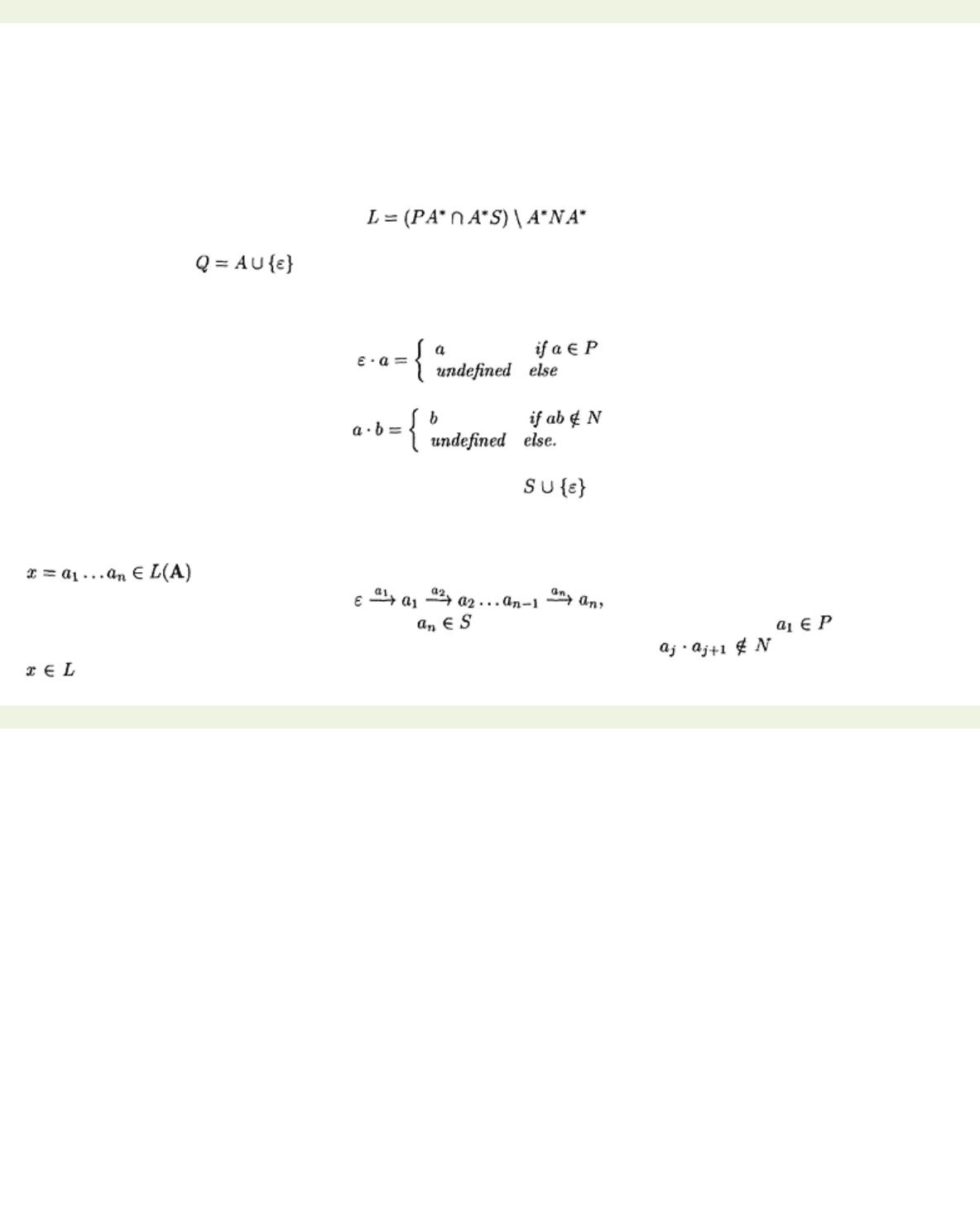
Theorem 6.1.4

Let

be a local language. Define an automaton

as follows:

•

The set of states .

•

The initial state is ε.

•

The terminal states are S.

•

The transitions are defined as follows:

and

Then

is a standard local automaton recognising L

If L contains the empty string, then

is defined as

above except that the terminal states are defined to be

Conversely, every language recognised

by a (standard) local automaton is local

Proof The automaton is local because for each state

and each input letter

either

is not defined

or it equals

. By construction the automaton is standard. It remains to prove that

(A)=

. Let

. Then there is a path in A labelled as follows:

where

is a terminal state. It follows that . Likewise,

1 is defined and so . Finally, for

each j such that 1≤

≤

−1 the fact that

+1 is defined implies that . It follows that

. Conversely, let

< previous page page_130 next page >

< previous page page_131 next page >

Page 131

. Then

and for each

such that 1≤

≤

−1 we have that . It

follows that

is a path in A from the initial state to a terminal state. Thus .

We conclude by proving that every language recognised by a local automaton is local. Let A=

(Q, A, q

δ, T)

be a local automaton recognising the language

(A). Define the following sets based on the

definition of A:

•

(PA

Let

…an

be a non-empty string in

(A). It is easy to check that . Conversely, let

. We show that

is accepted by A, so that . By assumption, and

and for each 1≤

≤

−1 we have that . Since we have that

0·

1 is defined. Put

0·

1. Since we have that

2 must label some path in A. Thus there are states

p, q

and

such that

Now

1 is defined as is

0·

1. But A is local and so

0·

1. Thus

1·

2 is defined. Put

1·

2. This same idea can be repeated with

3. Continuing in this way, we see that

…an

labels a path in A starting at

0 and finishing at a terminal state. Thus . It follows that

{ε}

and so

is a local language.

Thus the languages recognised by Myhill graphs are the local languages without

Example 6.1.5 Let

{a, b, c}, P

{a, b}, S

{a, c}

and

{ab, bc, ca}

. We use Theorem 6.1.4, to

construct a deterministic automaton to recognise

There are four states labelled

ε, a, b, c;

the initial state is

and the terminal states are

a, c,

the

elements of

. Thus we have so far constructed

< previous page page_131 next page >

< previous page page_132 next page >

Page 132

We now have to calculate the transitions. The only transitions emerging from

are those labelled

and

the elements of

which go to the states

and

respectively. We now calculate the transitions

emerging from the state

. Observe that whereas . Thus there are two transitions

emerging from state

one labelled

and one labelled

. To calculate the transitions emerging from

state

observe that whereas . Thus there are two transitions emerging from state

one labelled

and one labelled

. Finally, we calculate the transitions emerging from state

. We have

that but . Thus there are two transitions emerging from state

labelled

and

. The

resulting standard local automaton is therefore

Local languages are special kinds of recognisable languages. However, they can be used to obtain

another characterisation of arbitrary recognisable languages. To do this, we shall use monoid

homomorphisms introduced in Section 4.2. In fact, we need monoid homomorphisms having the

following property. A monoid homomorphism

α: A

*→

* is

strictly alphabetic

α(a)

is a letter in

for

each letter .

Theorem 6.1.6

Let be a recognisable language such that . Then there is an alphabet A, a

local language

, and a strictly alphabetic monoid homomorphism α: A

*→

such that α(K)

L contains ε then α

(

Proof Let B=

(S, B, s

, δ, T)

be an automaton that recognises

. The alphabet

is defined to be

the set of all transitions of B. The monoid homomorphism

α: A

*→

* is defined by

which is evidently strictly alphabetic. We shall now define the language

. Two triples,

< previous page page_132 next page >

< previous page page_133 next page >

Page 133

describe a consecutive pair of transitions in B if and only

1·

2. We define

as follows:

the

non-consecutive

transitions in B. Define

the set of transitions beginning at the initial state, and

the set of transitions that end at a terminal state. Then the language,

consists of all sequences of transitions in B that begin at

0 and end at a terminal state. Thus if

we have immediately that

α(K)

. If then we need to add

to our language

The theorem above can be paraphrased in the following terms: the language needed to describe an

automaton is simpler than the language the automaton describes; this makes sense: the syntax of a

programming language is easier to understand than what the programs written in that language

accomplish. If this were not true, why write the programs?

Example 6.1.7 Here is a concrete example of Theorem 6.1.6. Consider the automaton B given by the

transition table below:

The new alphabet

is given by

The set

is given by

and the set

is given by

Finally,

consists of the following strings of length 2 over the alphabet

< previous page page_133 next page >

< previous page page_134 next page >

Page 134

Define

Consider now the string

abab,

which is accepted by B. This corresponds to the sequence of transitions,

which clearly belongs to the language

Exercises 6.1

1. Complete the proof of Theorem 6.1.3 by checking that the two constructions described do not alter

the languages involved.

2. Construct standard local automata to recognise the following languages over the alphabet

{a, b}

(i)

(aA

(ii)

(aA

(iii)

(aA

)

3. Complete the proof of Theorem 6.1.4 by checking that the theorem holds when the local language

contains the empty string.

6.2 Linearisation

Regular expressions describe recognisable languages and, as we have seen, each recognisable language

is an image of a local language; in addition, it is easy to construct an automaton recognising a local

language. This raises the possibility of finding an algorithm for converting regular expressions into finite

automata that makes use of local automata. The goal of this section is to show how this can be

achieved. The linchpin of the construction is the notion of a ‘linear regular expression.’ A regular

expression

over an alphabet

is said to be

< previous page page_134 next page >

< previous page page_135 next page >

Page 135

linear

if each letter occurs at most once in

. For example, (

is a linear regular

expression over the alphabet

{a, b, c, d, e, f, g}

Linear regular expressions describe only a limited class of languages; we shall say more about which

languages these are below. However, with any regular expression we can easily associate a linear

regular expression over a larger alphabet by means of a simple-minded trick. Let

be a regular

expression over the alphabet

. Define a new regular expression

r′

as follows:

r′

is constructed from

replacing the

th letter

occurring in

from the left by

. We call

r′

the

linearisation

. For example,

let

ab(ba)

(ac)

]*. Then the linearisation of

which is a regular expression over the alphabet

, b

, a

, c

, b

}

The first plank of our argument is that from a deterministic automaton A′ recognising

r′,

one can easily

construct a (non-deterministic) automaton A recognising

in the following way: simply replace each

letter

labelling a transition of A′ by the corresponding letter

. Thus the problem of constructing an

automaton from a regular expression

reduces to the problem of constructing a deterministic automaton

from the linearisation of

. The second plank of our argument is provided by the following theorem.

Theorem 6.2.1

Let r be a linear regular expression. Then the language L(r) is local.

Proof Linear regular expressions are special kinds of regular expressions and so we can prove things

about them inductively. First we need three subsidiary results.

(1)

Let be two disjoint subsets of our alphabet A, and let and

be two local

languages. Then L

is a local language

Let A1=

, A

, i

, δ

, T

)

be a standard local automaton recognising

1 and let A2=

, A

, i

, δ

)

be a standard local automaton recognising

2. We construct a standard local automaton A=

(Q, A, i,

δ, T)

to recognise

2 as follows. Let

consist of the elements of

}

and

}

together with

a new initial state

. The transitions of A are as follows: all transitions of A1 except those transitions that

begin at

together with all the transitions of A2 except those transitions that begin at

together with

the following new transitions:

whenever is a transition in A1 or is a transition in

A2. Finally, the set of terminal states is defined to be

as long as neither

1 nor

2 is terminal,

otherwise it is defined to be

It is easy to see that A is a standard local automaton accepting

< previous page page_135 next page >

< previous page page_136 next page >

Page 136

(2)

Let be two disjoint subsets of our alphabet A, and let and be two local

languages. Then L

is a local language

Let A1=

, A

, i

, δ

, T

)

be a standard local automaton recognising

1 and let A2=

, A

, i

, δ

)

be a standard local automaton recognising

2. We construct a standard local automaton A=

(Q, A, i,

δ, T)

recognising

2 as follows. The set of states is the set (

2)\

}

and the initial state is

The transitions consist of all the transitions of A1, all the transitions of A2 that do not begin at

together with the following new transitions: if and if is a transition of A2. The

set of terminal states is

2 if and is if . It is easy to check that A is a

standard local automaton accepting

2. This construction is simply a variant of the construction used

to prove Proposition 3.3.4.

(3)

Let L be a local language. Then L

is a local language

Let A=

(Q, A, i, δ, T)

be a standard local automaton recognising

. Define as

follows: the transitions of A′ consist of all the transitions of A together with the transitions

where

and where is a transition in A. Then A′ is a standard local automaton recognising

*. This

construction is simply a variant of the one used to prove Proposition 3.3.6.

We can now prove our claim that if

is linear then

L(r)

is local. We do so by induction on the number of

operators in

. The languages

, ε,

and

where are each local. Suppose that all linear regular

expressions with at most

operators represent local languages. Let

be a regular linear expression with

+1 operators. We prove that

L(r)

is local. The expression

has one of three possible forms:

st,

*. Clearly

and

are both linear regular expressions with at most

operators apiece. Let

be the set of letters occurring in

and

be the set of letters occurring in

. Then since

is linear

and

are disjoint. It follows from results (1) and (2) above that

L(r)

L(s)

L(t)

and

L(r)

L(s)L(t)

are both

local. The fact that

L(r)

L(s)

* is local follows by result (3).

The above theorem suggests the following algorithm.

Algorithm 6.2.2 This algorithm takes as input a regular expression

and produces as output a non-

deterministic automaton A recognising

L(r)

. First, linearise

to obtain a linear regular expression

r′

Then construct a standard local automaton A′ recognising

L(r′)

. Finally, convert A′ into a non-

deterministic automaton A by relabelling the edges of A′.

This algorithm will be complete if we can find an algorithm for constructing the automaton described in

Theorem 6.1.4 from a linear regular expression

. This requires that we construct the sets

P(L(r)),

S(L(r)),

and

F(L(r));

in addition, we need to know whether . To do this we shall use the

following definitions. Let

be an alphabet and let

be a regular expression over

. We make the

following definitions:

< previous page page_136 next page >