Lallart M. Ferroelectrics: Characterization and Modeling

Подождите немного. Документ загружается.

First-principles Study of ABO

: Role of the B–O Coulomb Repulsions for Ferroelectricity and Piezoelectricity 5

a. Note that the fully optimized sturucture of BaTiO

is tetragonal with the Ti3spd4s PP,

whereas it is cubic (Pm

3m) with the Ti3d4s PP. As shown in Fig. 1(a) and 1(b), c/a and δ

show signiﬁcantly different results for a  3.7 whereas they show almost the same results for

 3.7 , for both Ti PPs. This result suggests that the optimized results of ABO

with smaller

lattice parameters, e.g., under high pressure (Bévillon et al., 2007), are almost independent of

the choice of PP.

㻔㼍㻕䠄㼎䠅

㻻

㼦

㻻

㼦

㼀㼕

㻻

㼤

㼀㼕㻻

㼤

Fig. 3. Two-dimentional electron-density contour map on the xz-plane for tetragonal BaTiO

(a) with the Ti3spd4s PP, and (b) with the Ti3d4s PP. The optimized calculated results with a

ﬁxed to be 3.8 are shown in both ﬁgures. The electron density increases as color changes from

blue to red via white. Contour curves are drawn from 0.4 to 2.0 e/

with increments of

0.2 e/

(Miura et al., 2010a).

The calculated results shown in Fig. 1 suggest that the explicit treatment of T i 3s and 3p

semicore states is essential to the appearance of ferroelectric states in BaTiO

. In the following,

the author investigates the role of Ti 3s and 3p states for ferroelectricity from two viewpoints.

One viwpoint concerns hybridizations between Ti 3s and 3p states and other states. Figure 2

shows the total density of states (DOS) of tetragonal BaT iO

with two Ti PPs. Both results are

in good agreement with previous calculated results (Chen et al., 2004; Khenata et al., 2005)

by the full-potential linear augmented plane wave (FLAPW) method. In the DOS with the

Ti3spd4s PP, the energy “levels", not bands, of Ti 3s and 3p states, are located at

−2.0 Hr

and

−1.2 Hr, respectively. This result suggests that the Ti 3s and 3p orbitals do not make any

hybridizations but only give Coulomb repulsions with the O orbitals as well as the Ba orbitals.

In the DOS with the Ti3d4s PP, on the other hand, the energy levels of Ti 3s and 3p states are

not shown because Ti 3s and 3p states were treated as the core charges. This result means that

the Ti 3s and 3p orbitals cannot even give Coulomb repulsions with the O orbitals as well as

the Ba orbitals.

Another viwpoint is about the Coulomb repulsions between Ti 3s and 3p

x (y)

states and

x (y)

2s and 2p

x (y)

states in tetragonal BaTiO

. Figures 3(a) and 3(b) show two-dimentional

electron-density contour map on the xz-plane for tetragonal BaTiO

with the Ti3spd4s PP, and

that with the Ti3d4s PP, respectively. These are the optimized calculated results with a ﬁxed

399

First-Principles Study of ABO

: Role of the

B–O Coulomb Repulsions for

Ferroelectricity and Piezoelectricity

6 Ferroelectrics

㻔㼍㻕㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻌㻔㼎㻕

㼦

㻻

㼦

㻻

㼦

㻻

㼦

㻻

㼦

㻞㼟

㻞㼜

㼦

㼤

㻻

㼤

㻻

㼦

㻟㼜

㼤

㻞㼜

㼤

㻟㼟

㼀㼕

㻟㼜

㼦

㻞㼟

㻯㼛㼡㼘㼛㼙㼎

㼞㼑㼜㼡㼘㼟㼕㼛㼚

㼤

㻻

㼤

㻻

㼦

㻟㼜

㼤

㻞㼜

㼤

㻟㼟

㼀㼕

㻟㼜

㼦

㻞㼟

㻯㼛㼡㼘㼛㼙㼎

㼞㼑㼜㼡㼘㼟㼕㼛㼚

㼤

㼀㼕

㻻

㼤

㼦

㻟㼜

㼤

㻞㼜

㼤

㻟㼟

㻯㼛㼡㼘㼛㼙㼎㻌㼞㼑㼜㼡㼘㼟㼕㼛㼚

㻞㼟

㼤

㼀㼕

㻻

㼤

㼦

㻟㼜

㼤

㻞

㼤

㻞㼜

㼦

㻟㼜

㼦

㼞㼑㼜㼡㼘㼟㼕㼛㼚㼞㼑㼜㼡㼘㼟㼕㼛㼚

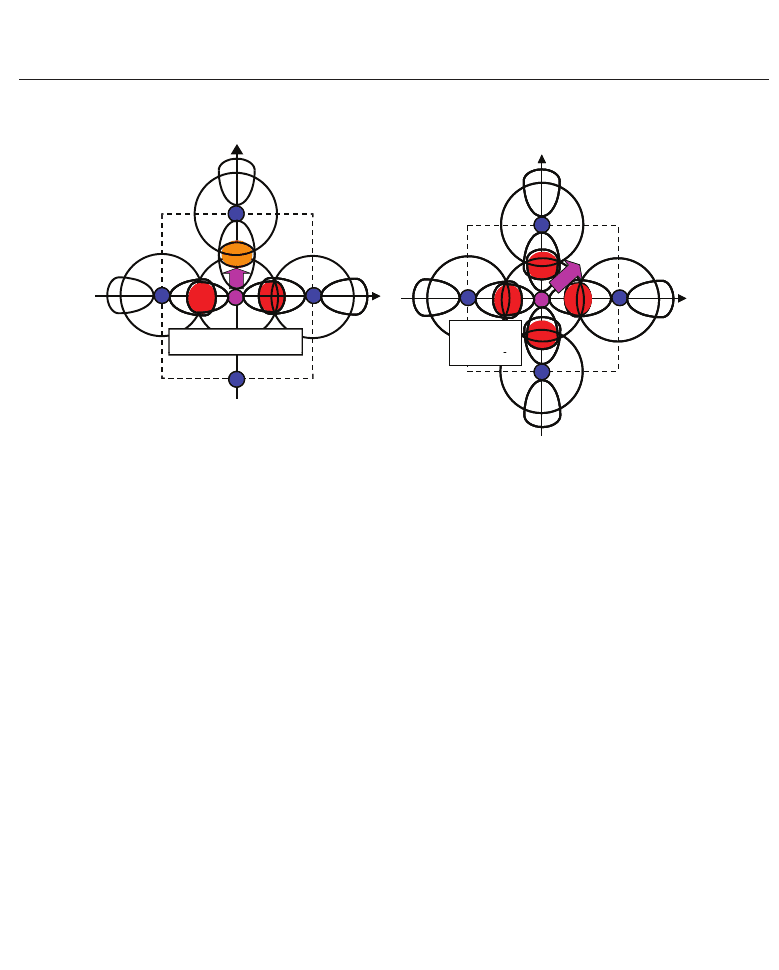
Fig. 4. Illustrations of the proposed mechanisms for the Coulomb repulsions between Ti 3s

and 3p states and O 2s and 2p states in BaTiO

: (a) anisotropic Coulomb repulsions between

Ti 3s and 3p

x (y)

states and O

x (y)

2s and 2p

x (y)

states, and between Ti 3s and 3p

states and

2s and 2p

states, in the tetragonal structure. (b) isotropic Coulomb repulsions between

Ti 3s and 3p

x (y)(z)

states and O

x (y)(z)

2s and 2p

x (y)(z)

states, in the rhombohedral

structure (Miura et al., 2010a).

to be 3.8 , and the electron density in Fig. 3(a) is quantitatively in good agreement with the

experimental result (Kuroiwa et al., 2001). The electron density between Ti and O

ions in

Fig. 3(a) is larger than that in Fig. 3(b), which suggests that Ti ion displacement is closely

related to the Coulomb repulsions between Ti 3s and 3p states and O 2s and 2p states along

the [001] axis (the z-axis in this case).

The present discussion of the Coulomb repulsions is consistent with the previous reports. A

recent soft mode investigation (Oguchi et al., 2009) of BaTiO

shows that Ba ions contribute

little to the appearance of T i ion displacement along the [001] axis. This result suggests that Ti

ion displacement is closely related to the structural distortion of TiO

octahedra. In the present

calculations, on the other hand, the only difference between BaTiO

with the Ti3spd4s PP

and with the Ti3d4s PP is the difference in the expression for the Ti 3s and 3p states, i.e.,

the explicit treatment and including core charges. However, our previous calculation (Miura

& Tanaka, 1998) shows that the strong Coulomb repulsions between Ti 3s and 3p

states and

2s and 2p

states do not favour Ti ion displacement along the [001] axis. This result suggests

that the Coulomb repulsions between T i 3s and 3p

x (y)

states and O

x (y)

2s and 2p

x (y)

states

would contribute to Ti ion displacement along the [001] axis, and the suggestion is consistent

with a recent calculation (Uratani et al., 2008) for PbTiO

indicating that the tetragonal and

ferroelectric structure appears more favourable as the a lattice parameter decreases.

Considering the above investigations, the author proposes the mechanism of Ti ion

displacement as follows: Ti ion displacement along the z-axis appears when the Coulomb

repulsions between Ti 3s and 3p

x (y)

states and O

x (y)

2s and 2p

x (y)

states, in addition to the

dipole-dipole interaction, overcome the Coulomb repulsions between Ti 3s and 3p

states and

2s and 2p

states (Miura & Tanaka, 1998). An illustration of the Coulomb repulsions is

shown in Fig. 4(a). In fully optimized BaTiO

with the Ti3spd4s PP, the Ti ion can be displaced

due to the above mechanism. In fully optimized BaT iO

with the Ti3d4s PP, on the other

㻔㼍㻕㻔㼎㻕

400

Ferroelectrics - Characterization and Modeling

First-principles Study of ABO

: Role of the B–O Coulomb Repulsions for Ferroelectricity and Piezoelectricity 7

hand, the Ti ion cannot be displaced due to the weaker Coulomb repulsions between Ti and

x (y)

ions. However, since the Coulomb repulsion between Ti and O

ions in BaTiO

with the

Ti3d4s PP is also weaker than that in BaTiO

with the Ti3spd4s PP, the Coulomb repulsions

between between Ti and O

x (y)

ions in addition to the log-range force become comparable

to the Coulomb repulsions between Ti and O

ions both in Ti PPs, as the lattice parameter

a becomes smaller. The above discussion suggests that the hybridization between Ti 3d and

2s and 2p

stabilizes Ti ion displacement, but contribute little to a driving force for the

appearance of Ti ion displacement.

It seems that the above proposed mechanism for tetragonal BaTiO

can be applied to the

mechanism of Ti ion displacement in rhombohedral BaTiO

, as illustrated in Fig. 4(b). The

strong isotropic Coulomb repulsions between Ti 3s and 3p

x (y)(z)

states and O

x (y)(z)

2s and

x (y)(z)

states yield T i ion displacement along the [111] axis. On the other hand, when

the isotropic Coulomb repulsions are weaker or stronger, the Ti ion cannot be displaced and

therefore it is favoured for the crystal structure to be cubic.

㻜㻚㻟

㻜㻚㻟㻡

㻝

㻝㻚㻞

㻝㻚㻠

㻔㼍㻕㻔㼎㻕

㻾㻟㼙㻌㻮㼍㼀㼕㻻

㻟

㻦㻌㻥㻜㻙䃐㻌㼢㻚㼟㻚㻌㼂㻛㼂

㼞㼔㼛㼙㼎㼛

㻾㻟㼙㻌㻮㼍㼀㼕㻻

㻟

㻦㻌䃓

㼀㼕

㼢㻚㼟㻚㻌㼂㻛㼂

㼞㼔㼛㼙㼎㼛

㼓

㻚㻕

㻜

㻜㻚㻜㻡

㻜㻚㻝

㻜㻚㻝㻡

㻜㻚㻞

㻜㻚㻞㻡

㻜㻤

㻜㻥

㻝

㻝㻝

㻝㻞

㻝㻟

㻝㻠

㻜

㻜㻚㻞

㻜㻚㻠

㻜㻚㻢

㻜㻚㻤

㻝

㻜㻤

㻜㻥

㻝

㻝㻝

㻝㻞

㻝㻟

㻝㻠

䃓

㼀㼕

㻔䊅㻕

㻥㻜㻌䇵䃐㻌㻔㼐㼑

㼓

㻜

㻚

㻤

㻜

㻚

㻥

㻝

㻚

㻝

㻚

㻞

㻝

㻚

㻟

㻝

㻚

㻠

㻜

㻚

㻤

㻜

㻚

㻥

㻝

㻚

㻝

㻚

㻞

㻝

㻚

㻟

㻝

㻚

㻠

㼂㻛㼂

㼞㼔㼛㼙㼎㼛

㼂㻛㼂

㼞㼔㼛㼙㼎㼛

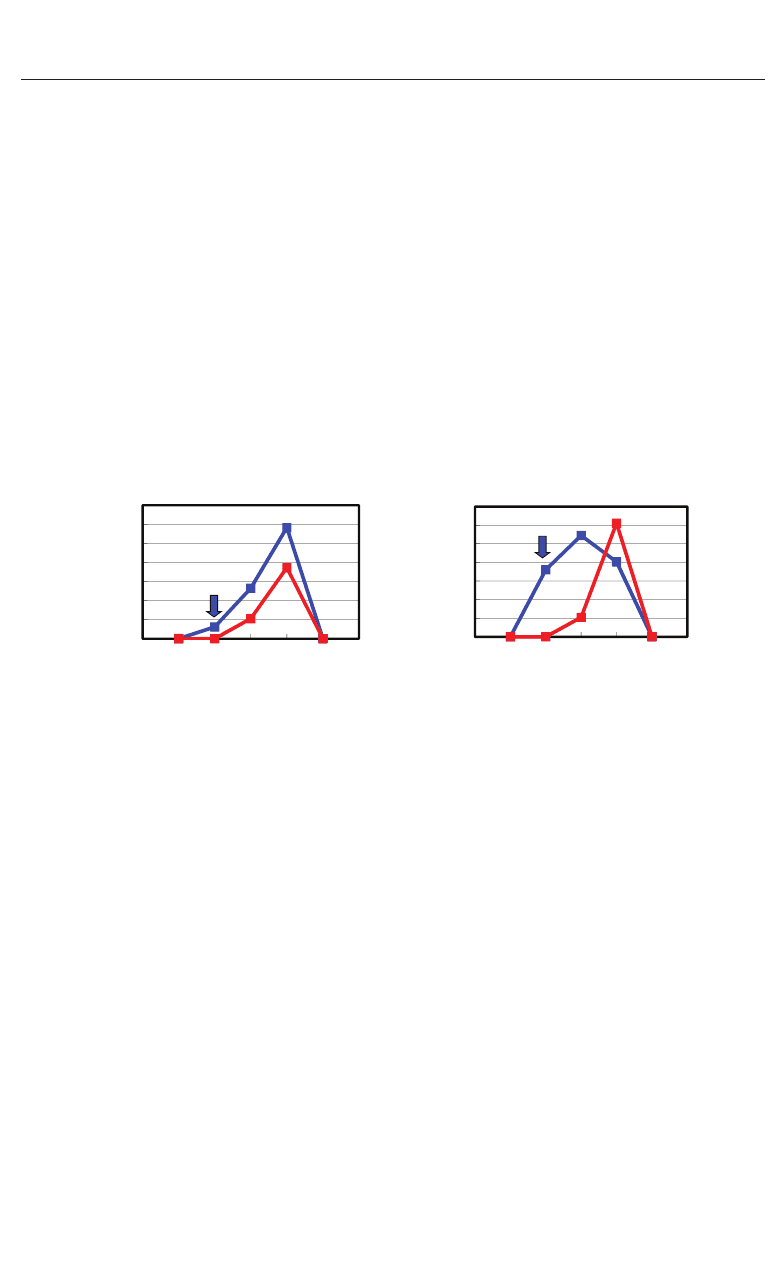
Fig. 5. Optimized calculated results as a function of the ﬁxed volumes of the unit cells in

rhombohedral BaTiO

: (a) 90−α degree and (b) δ

to the [111] axis. Blue lines correspond to

the results with the Ti3spd4s PP, and red lines correspond to those with the T i3d4s PP.

rhombo

denote the volume of the fully optimized unit cell with the Ti 3spd4s PP. Results with

arrows are the fully optimized results, and the other results are those with all the inner

coordinations optimized for ﬁxed volumes of the unit cells (Miura et al., 2010a).

Let us investigate the structural properties of rhombohedral BaTiO

. Figures 5(a) and 5(b)

show the optimized results of the 90

−α degree and δ

as a function of ﬁxed volumes of

the unit cells in rhombohedral BaTiO

, respectively, where α denotes the angle between

two lattice vectors. In these ﬁgures, α denotes the angle between two crystal axes of

rhombohedral BaTiO

,andδ

denotes the value of the Ti ion displacement along the [111]

axis. Results with arrows are the fully optimized results; V

rhombo

denote the volume of the

fully optimized unit cell with the Ti 3spd4s PP. The other results are those with all the inner

coordinations optimized with ﬁxed volumes of the unit cells. The proposal mechanisms about

the Coulomb repulsions seem to be consistent with the calculated results shown in Fig. 5: For

V/V

rhombo

 0.9 or  1.3, the isotropic Coulomb repulsions are weaker or stronger, and the

Ti ion cannot be displaced along the [111] axis and therefore the crystal structure is cubic for

both Ti PPs. For 0.9

 V/V

rhombo

 1.3, on the other hand, the isotropic Coulomb repulsions

401

First-Principles Study of ABO

: Role of the

B–O Coulomb Repulsions for

Ferroelectricity and Piezoelectricity

8 Ferroelectrics

are strong enough to yield Ti ion displacement for both Ti PPs. However, since the magnitude

of the isotropic Coulomb repulsion is different in the two Ti PPs, the properties of the 90

−α

degree and δ

are different quantitatively.

3.2 Role of the Ti–O Coulomb repulsions for piezoelectric SrTiO

and BaTiO

As discussed in the previous subsection, the Coulomb repulsions between Ti 3s and 3p

x (y)

states and O

x (y)

2s and 2p

x (y)

states have an important role in the appearance of the

ferroelectric state in tetragonal BaTiO

. In this subsection, the author discusses the role of

the Ti–O Coulomb repulsions for piezoelectric SrTiO

and BaTiO

㻜㻢

㻜㻚㻤㻌

㻝㻚㻜㻌

㼙

㼊㻞㻕

㻔㼍㻕㻔㼎㻕

㻝㻚㻞㻜㻌

㻝㻚㻟㻜㻌

㼙

㻞

㻕

㼏㻛㼍㻌㼢㻚㼟㻚㻌㼍

㻼

㻟

㼢㻚㼟㻚㻌㼍

㻮㼍㼀㼕㻻

㻟

㻮㼍㼀㼕㻻

㻟

㻜㻚㻜㻌

㻜㻚㻞㻌

㻜㻚㻠㻌

㻜

㻚

㻢

㻌

㻟㻚㻢㻌㻟㻚㻣㻌㻟㻚㻤㻌㻟㻚㻥㻌㻠㻚㻜㻌

㻼㻟㻌㻔㻯㻛

㼙

㻔㻭㻕

㻝㻚㻜㻜㻌

㻝㻚㻝㻜㻌

㻟㻚㻢㻌㻟㻚㻣㻌㻟㻚㻤㻌㻟㻚㻥㻌㻠㻚㻜㻌

㼏㻛㼍

㼍㻔㻭㻕

㻼

㻟

㻔㻯㻛

㼙

㻿㼞㼀㼕㻻

㻟

㻿㼞㼀㼕㻻

㻟

㼏㻛㼍㻌

㼍㻌

㻔㻭㻕

㼍

㻌

㻔㻭㻕

㼍㻌㻔䊅㻕㼍㻌㻔䊅㻕

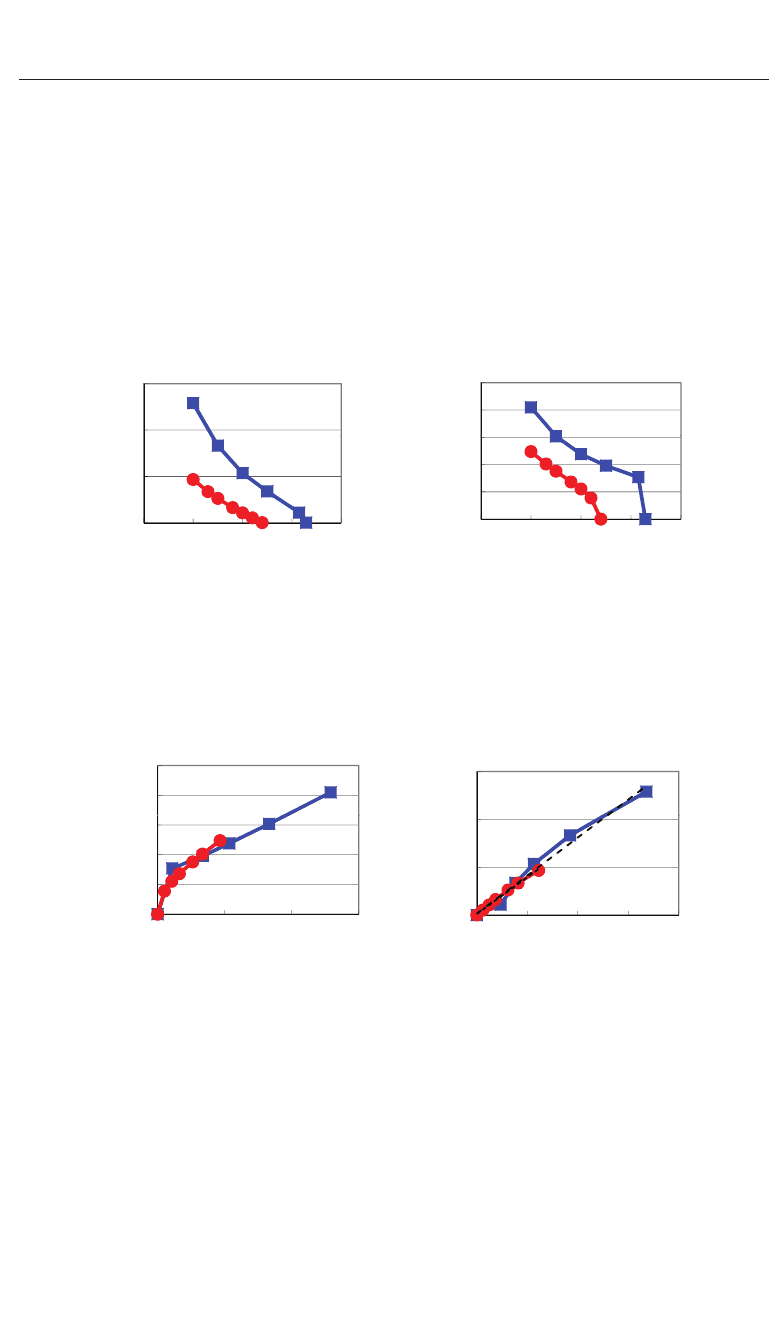
Fig. 6. Optimized calculated results as a function of a lattice parameters in compressive

tetragonal SrTiO

and BaTiO

:(a)c/a ratio and (b) P

, i.e., spontaneous polarization along

the [001] axis (Furuta & Miura, 2010).

㻜㻚㻤㻌

㻝㻚㻜㻌

㻕

㻜㻞㻜

㻜㻚㻟㻜㻌

㻔㼍㻕㻔㼎㻕

㻼

㻟

㼢㻚㼟㻚㻌㼏㻛㼍

㻕

㻮㼍㼀㼕㻻

㻟

㻮㼍㼀㼕㻻

㻟

㼏㻛㼍㻌䇵㻝㻌㼢㻚㼟㻚㻌㻼

㻟

㻞

㻜㻚㻜㻌

㻜㻚㻞㻌

㻜㻚㻠㻌

㻜㻚㻢㻌

㻝㻚㻜㻜

㻝㻚㻝㻜

㻝㻚㻞㻜

㻝㻚㻟㻜

㻼㻟㻌㻔㻯㻛㼙㼊㻞

㻕

㻜㻚㻜㻜㻌

㻜㻚㻝㻜㻌

㻜

㻚

㻞㻜

㻌

㻜㻜

㻜㻞

㻜㻠

㻜㻢

㻜㻤

㼏㻛㼍㻌㻙㻝

㻼

㻟

㻔㻯㻛㼙

㻞

㻕

㻿㼞㼀㼕㻻

㻟

㻿㼞㼀㼕㻻

㻟

㼏㻛㼍㻌㻙㻝

㻝㻚㻜㻜

㻌

㻝㻚㻝㻜

㻌

㻝㻚㻞㻜

㻌

㻝㻚㻟㻜

㻌

㼏㻛㼍

㻜

㻚

㻜

㻌

㻜

㻚

㻞

㻌

㻜

㻚

㻠

㻌

㻜

㻚

㻢

㻌

㻜

㻚

㻤

㻌

㻼㻟㼊㻞㻌㻔㻯㼊㻞㻛㼙㼊㻠㻕

㻼

㻟

㻞

㻔㻯

㻞

㻛㼙

㻠

㻕

Fig. 7. (a) P

as a function of c/a ratios, and (b) c/a ratio as a function of P

.Thesevaluesare

derived from the calculated results as shown in Figs. 6(a) and (b). Dotted and dashed lines in

Fig. 7(b) serve as visual guides for SrTiO

and BaTiO

, respectively (Furuta & Miura, 2010).

Figures 6(a) shows the optimized results for the ratio c/a as a function of the a lattice

parameters in tetragonal SrTiO

and BaTiO

. These results are the fully optimized results

and the results with the c lattice parameters and all the inner coordinations optimized for

㻜㻚㻡㻌

㻝㻚㻜㻌

㻕

㻔㼍㻕㻔㼎㻕

㻮㼍㼀㼕㻻

㻟

㻞

㻕

㼑

㻟㻝

㼢㻚㼟㻚㻌㼏㻛㼍

㻝㻞㻚㻜㻌

㻝㻢㻚㻜㻌

㻞㻕

㻞

㻕

㼑

㻟㻟

㼢㻚㼟㻚㻌㼏㻛㼍

㻿㼞㼀㼕㻻

㻟

㻙㻝㻚㻜㻌

㻙㻜㻚㻡㻌

㻜㻚㻜㻌

㻝㻚㻜㻜㻌㻝㻚㻝㻜㻌㻝㻚㻞㻜㻌㻝㻚㻟㻜㻌

㼑㻟㻝㻌㻔㻯㻛㼙㼊

㻿㼞㼀㼕㻻

㻟

㼑

㻟㻝

㻔㻯㻛

㻜㻚㻜㻌

㻠㻚㻜㻌

㻤㻚㻜㻌

㻝㻚㻜㻜㻌㻝㻚㻝㻜㻌㻝㻚㻞㻜㻌㻝㻚㻟㻜㻌

㼑㻟㻟㻌㻔㻯㻛㼙㼊

㼑

㻟㻟

㻔㻯㻛

㻮㼍㼀㼕㻻

㻟

㼏㻛㼍

402

Ferroelectrics - Characterization and Modeling

First-principles Study of ABO

: Role of the B–O Coulomb Repulsions for Ferroelectricity and Piezoelectricity 9

ﬁxed a. The fully optimized parameters of SrTiO

( a = 3.84 : cubic) and BaTiO

( a =3.91

and c = 4.00 : tetragonal) are within 2.0% in agreement with the experimental results in room

temperature. Figures 6(b) shows the evaluated results for P

as a function of the a lattice

parameters in tetragonal SrTiO

and BaTiO

,whereP

, which is evaluated by eq. (2), denotes

the spontaneous polarization along the [001] axis. Note that the tetragonal and ferroelectric

structures appear even in SrTiO

when the ﬁxed a lattice parameter is compressed to be

smaller than the fully-optimized a lattice parameter. As shown in Figs. 6(a) and 6(b), the

tetragonal and ferroelectric structure appear more favorable as the ﬁxed a lattice parameter

decreases, which is consistent with previous calculated results (Miura et al., 2010a; Ricinschi

et al., 2006; Uratani et al., 2008). The results would be due to the suggestion discussed in the

previous section that the large Coulomb repulsion of Ti–O bondings along the [100] axis (and

the [010] axis) is a driving force of the displacement of Ti ions along the [001] axis, i.e., the large

Coulomb repulsion along the [100] axis (and the [010] axis) is essential for the appearance of

the tetragonal structure. Figure 7(a) shows the relationship between P

and the ratio c/a,

where P

and c/a are derived from the calculated results shown in Figs. 6(a) and 6(b). The

property of BaTiO

in Fig. 7(a) is in qualitatively agreement with a previous calculational

result (Ricinschi et al., 2006). Figure 7(b) shows the relationship between the ratio c/a and

.Notethatc/a − 1isproportionaltoP

with alomost the same coefﬁcients in both SrTiO

and BaTiO

. Clearly, the ratio c/a is a good parameter in both tetragonal SrTiO

and BaTiO

with in-plane compressive stress. Therefore, in the following, the author uses the ratio c/a as

a parameter for the investigations of the piezoelectric properties.

㻜㻚㻡㻌

㻝㻚㻜㻌

㻞

㻕

㻔㼍㻕㻔㼎㻕

㻮㼍㼀㼕㻻

㻟

㼙

㻞

㻕

㼑

㻟㻝

㼢㻚㼟㻚㻌㼏㻛㼍

㻝㻞㻚㻜㻌

㻝㻢㻚㻜㻌

㻞㻕

㼙

㻞

㻕

㼑

㻟㻟

㼢㻚㼟㻚㻌㼏㻛㼍

㻿㼞㼀㼕㻻

㻟

㻙㻝㻚㻜㻌

㻙㻜㻚㻡㻌

㻜㻚㻜㻌

㻝㻚㻜㻜㻌㻝㻚㻝㻜㻌㻝㻚㻞㻜㻌㻝㻚㻟㻜㻌

㼑㻟㻝㻌㻔㻯㻛㼙㼊

㻞

㻿㼞㼀㼕㻻

㻟

㼑

㻟㻝

㻔㻯㻛

㼙

㻜㻚㻜㻌

㻠㻚㻜㻌

㻤㻚㻜㻌

㻝㻚㻜㻜㻌㻝㻚㻝㻜㻌㻝㻚㻞㻜㻌㻝㻚㻟㻜㻌

㼑㻟㻟㻌㻔㻯㻛㼙㼊

㼑

㻟㻟

㻔㻯㻛

㼙

㻮㼍㼀㼕㻻

㻟

㼏㻛㼍

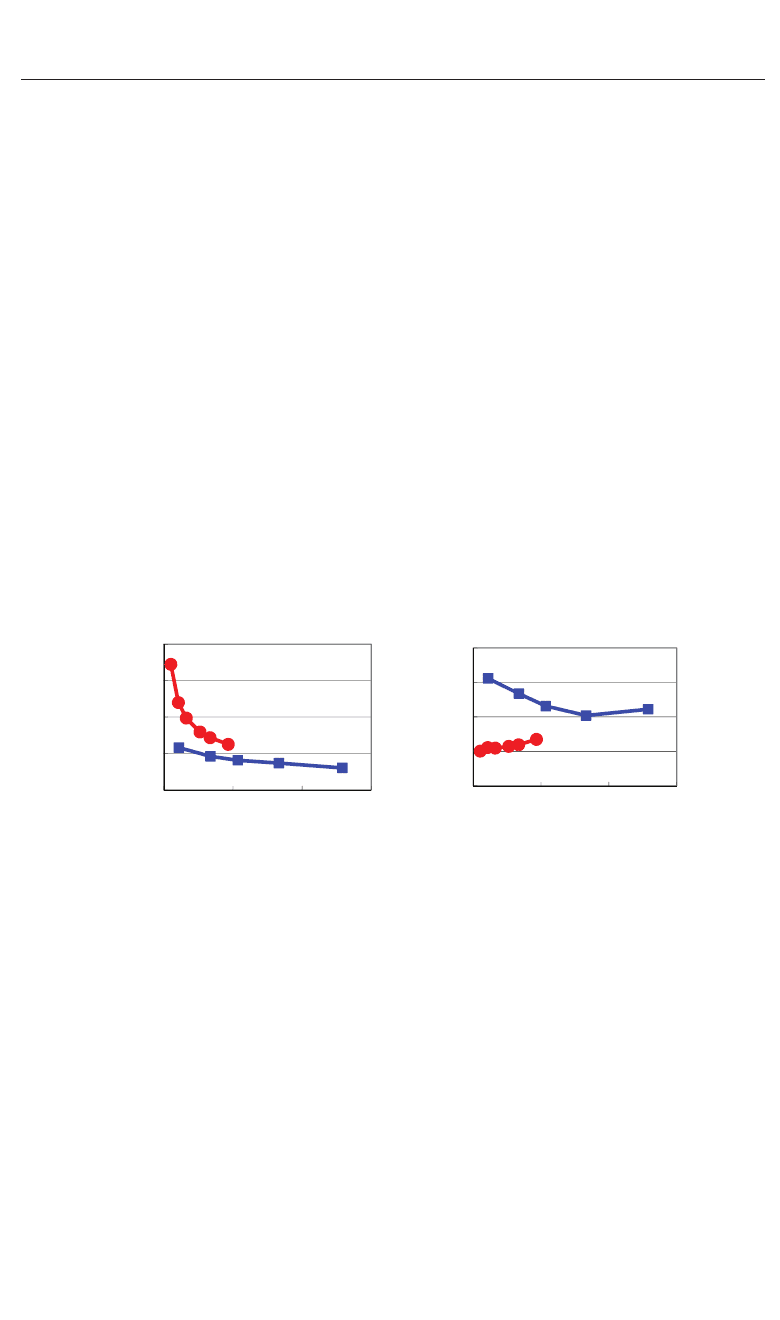
Fig. 8. Evaluated piezoelectric constants as a function of c/a ratios in optimized tetragonal

SrTiO

and BaTiO

:(a)e

and (b) e

(Furuta & Miura, 2010).

Figures 8(a) and 8(b) shows the piezoelectric properties of e

and e

as a function of the

ratio c/a in tetragonal SrTiO

and BaTiO

. The ratio c/a is optimized value as shown in

Fig. 6(a) and e

and e

are evaluated values in their optimized structures. Note that e

become larger at c/a ≈ 1, especially in SrTiO

. These properties seem to be similar to the

properties arond the Curie temperatures in piezoelectric ABO

; Damjanovic emphasized the

importance of the polarization extension as a mechanism of larger piezoelectric constants in

a recent paper (Damjanovic, 2010). Contrary to e

, on the other hand, the changes in e

are much smaller than the changes in e

, but note that e

shows negative in SrTiO

while

positive in BaTiO

403

First-Principles Study of ABO

: Role of the

B–O Coulomb Repulsions for

Ferroelectricity and Piezoelectricity

10 Ferroelectrics

㻞㻜

㻠㻚㻜㻌

㻢㻚㻜㻌

㻤㻚㻜㻌

㻟

㻮㼀㻻

㻞㻜

㻠㻚㻜㻌

㻢㻚㻜㻌

㻤㻚㻜㻌

㻟

㻿㼀㻻

㻔㼍㻕㻔㼎㻕

㻟

㼆

㻖

㻟㻟

㼢㻚㼟㻚㻌㼏㻛㼍㻌㼕㼚㻌㻿㼞㼀㼕㻻

㻟

㼆

㻖

㻟㻟

㼢㻚㼟㻚㻌㼏㻛㼍㻌㼕㼚㻌㻮㼍㼀㼕㻻

㻟

㼀㼕

㻿㼞

㼀㼕

㻙㻢㻚㻜㻌

㻙㻠㻚㻜㻌

㻙㻞㻚㻜㻌

㻜㻚㻜㻌

㻞

㻚

㻜

㻌

㻝㻚㻜㻜㻌㻝㻚㻝㻜㻌㻝㻚㻞㻜㻌㻝㻚㻟㻜㻌

㼆㻖㻟

㻟

㻛

㻙㻢㻚㻜㻌

㻙㻠㻚㻜㻌

㻙㻞㻚㻜㻌

㻜㻚㻜㻌

㻞

㻚

㻜

㻌

㻝㻚㻜㻜㻌㻝㻚㻝㻜㻌㻝㻚㻞㻜㻌㻝㻚㻟㻜㻌

㼆㻖㻟

㻟

㻛

㼆

㻖

㻟

㼆

㻖

㻟

㻻

㼤

㻻

㼦

㻮㼍

㻻

㼤

㻻

㼦

㼏

㻛

㼍㼏

㻛

㼍

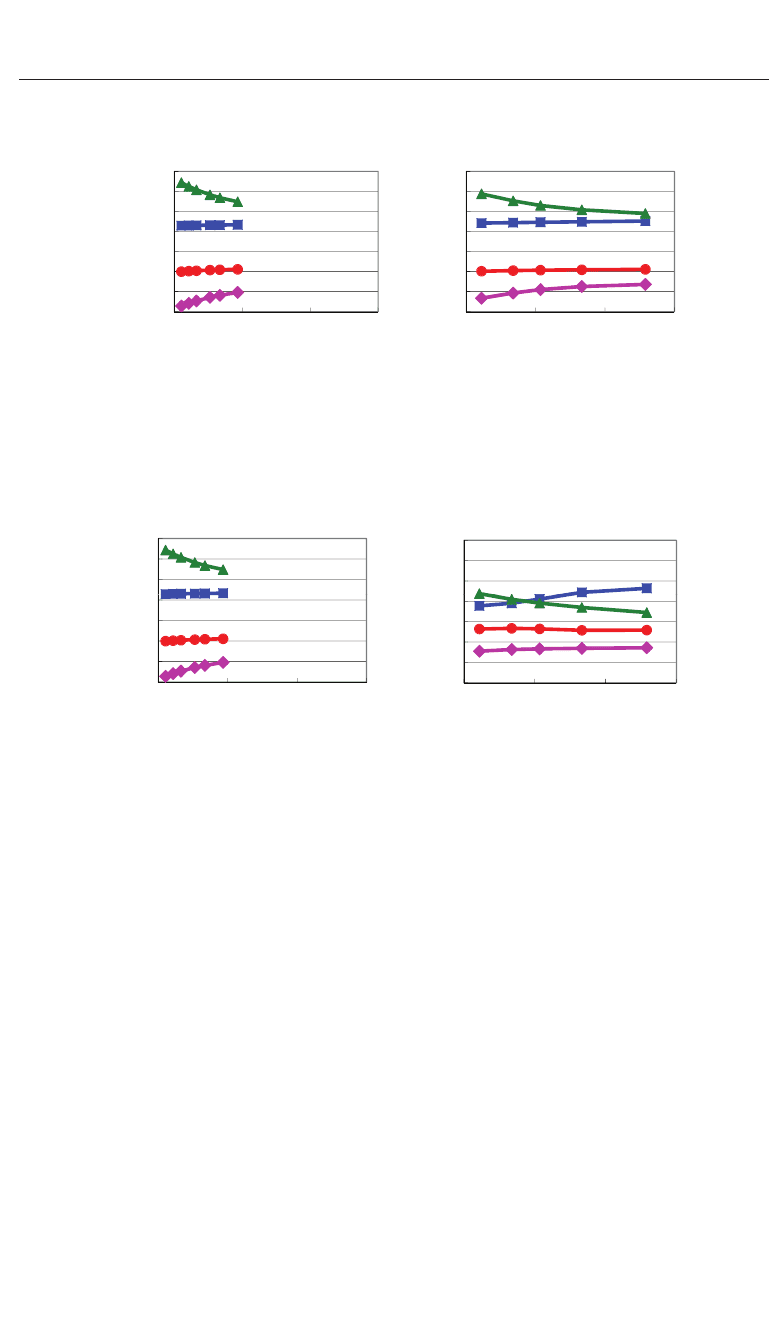
Fig. 9. Evaluated Born effective charges Z

∗

(k) as a function of c/a ratios: (a) SrTiO

and

(b) BaTiO

and O

denote oxygen atoms along the [100] axis and the [001] axis,

respectively (Furuta & Miura, 2010).

㻠㻚㻜㻌

㻢㻚㻜㻌

㻤㻚㻜㻌

䃖㻟

㻮㼀㻻

㻠㻚㻜㻌

㻢㻚㻜㻌

㻤㻚㻜㻌

㻟

㻿㼀㻻

㻔㼍㻕㻔㼎㻕

㻔㼍㻚㼡㻚㻕

䌖㼡

㻟

㻛䌖䃖

㻟

㼢㻚㼟㻚㻌㼏㻛㼍㻌㼕㼚㻌㻿㼞㼀㼕㻻

㻟

㼀㼕㻮㼍

㻿㼞

㼀㼕

䌖㼡

㻟

㻛䌖䃖

㻟

㼢㻚㼟㻚㻌㼏㻛㼍㻌㼕㼚㻌㻮㼍㼀㼕㻻

㻟

㻔㼍㻚㼡㻚㻕

㻙㻢㻚㻜㻌

㻙㻠㻚㻜㻌

㻙㻞㻚㻜㻌

㻜㻚㻜㻌

㻞㻚㻜㻌

㻝㻚㻜㻜㻌㻝㻚㻝㻜㻌㻝㻚㻞㻜㻌㻝㻚㻟㻜㻌

䌖㼡㻟㻛䌖

㻙㻢㻚㻜㻌

㻙㻠㻚㻜㻌

㻙㻞㻚㻜㻌

㻜㻚㻜㻌

㻞㻚㻜㻌

㻝㻚㻜㻜㻌㻝㻚㻝㻜㻌㻝㻚㻞㻜㻌㻝㻚㻟㻜㻌

㼆㻖㻟

㻟

䌖㼡

㻟

㻛䌖䃖

㻟

㻻

㼤

㻻

㼦

㻿㼞

㻻

㼤

㻻

㼦

䌖㼡

㻟

㻛䌖䃖

㻟

㼏㻛㼍

Fig. 10. Evaluated values of ∂u

(k)/∂η

as a function of c /a ratios: (a) SrT iO

and (b) BaT iO

“a.u." denotes the atomic unit (

≈ 0.53) (Furuta & Miura, 2010).

As expressed in eq. (4), e

is the sum of the contributions from the clamped term and the

relaxed term. However, it has been generally known that the contribution to e

from the

clamped term is much smaller than that from the relaxed term; in fact, the absolute values of

the e

clamped terms are less than 1 C/m

in both SrTiO

and BaTiO

. The author therefore

investigates the contributions to the relaxed term of e

and e

in detail. As expressed in

eq. (4), the relaxed terms of e

are proportional to the sum of the products between the Z

∗

(k)

and ∂u

(k)/∂η

(j = 3 or 1) values. Let us show the evaluated results of Z

∗

(k), ∂u

(k)/∂η

and ∂u

(k)/∂η

in the following. Figures 9(a) and 9(b) show the Z

∗

(k) values in SrTiO

and BaTiO

, respectively. Properties of the Z

∗

(k) values are quantitatively similar in both

SrTiO

and BaTiO

. Therefore, the difference in the properties of e

and e

between SrTiO

and BaTiO

must be due to the difference in the properties of ∂u

(k)/∂η

. Figures 10(a) and

10(b) show the ∂u

(k)/∂η

values in SrTiO

and BaTiO

, respectively. In these ﬁgures, O

and O

denote oxygen atoms along the [100] and [001] axes, respectively, and η

is deﬁned as

≡ (c − c

)/c

,wherec

denotes the c lattice parameter with fully optimized structure.

Clearly, the absolute values of ∂u

(k)/∂η

are d ifferent in between SrTiO

and BaTiO

.On

㻙

㻜㻚㻜㻌

㻝㻚㻜㻌

䃖㻝

㻜㻚㻜㻌

㻝㻚㻜㻌

䃖㻝

㻔㼍㻕㻔㼎㻕

㻔㼍㻚㼡㻚㻕

䌖㼡

㻟

㻛䌖䃖

㻝

㼢㻚㼟㻚㻌㼏㻛㼍㻌㼕㼚㻌㻿㼞㼀㼕㻻

㻟

㼀㼕㻮㼍

㻿㼞

㻻

㼦

䌖㼡

㻟

㻛䌖䃖

㻝

㼢㻚㼟㻚㻌㼏㻛㼍㻌㼕㼚㻌㻮㼍㼀㼕㻻

㻟

㻔㼍㻚㼡㻚㻕

㻙㻠㻚㻜㻌

㻙㻟㻚㻜㻌

㻙㻞㻚㻜㻌

㻚㻌

㻝㻚㻜㻜㻌㻝㻚㻝㻜㻌㻝㻚㻞㻜㻌㻝㻚㻟㻜㻌

䌖㼡㻟㻛䌖

㻙㻠㻚㻜㻌

㻙㻟㻚㻜㻌

㻙㻞㻚㻜㻌

㻚㻌

㻝㻚㻜㻜㻌㻝㻚㻝㻜㻌㻝㻚㻞㻜㻌㻝㻚㻟㻜㻌

䌖㼡㻟㻛䌖

䌖㼡

㻟

㻛䌖䃖

㻝

㻻

㼤

㼦

㼀㼕

㻻

㼤

䌖㼡

㻟

㻛䌖䃖

㻝

㼏㻛㼍

404

Ferroelectrics - Characterization and Modeling

First-principles Study of ABO

: Role of the B–O Coulomb Repulsions for Ferroelectricity and Piezoelectricity 11

㻙

㻝㻜

㻜㻚㻜㻌

㻝㻚㻜㻌

䃖㻝

㻮㼀㻻

㻙

㻝㻜

㻜㻚㻜㻌

㻝㻚㻜㻌

䃖㻝

㻿㼀㻻

㻔㼍㻕㻔㼎㻕

㻔㼍㻚㼡㻚㻕

䌖㼡

㻟

㻛䌖䃖

㻝

㼢㻚㼟㻚㻌㼏㻛㼍㻌㼕㼚㻌㻿㼞㼀㼕㻻

㻟

㼀㼕

㻻

㻮㼍

㻿㼞

㻻

㼦

䌖㼡

㻟

㻛䌖䃖

㻝

㼢㻚㼟㻚㻌㼏㻛㼍㻌㼕㼚㻌㻮㼍㼀㼕㻻

㻟

㻔㼍㻚㼡㻚㻕

㻙㻠㻚㻜㻌

㻙㻟㻚㻜㻌

㻙㻞㻚㻜㻌

㻝

㻚

㻜

㻌

㻝㻚㻜㻜㻌㻝㻚㻝㻜㻌㻝㻚㻞㻜㻌㻝㻚㻟㻜㻌

䌖㼡㻟㻛䌖

㻙㻠㻚㻜㻌

㻙㻟㻚㻜㻌

㻙㻞㻚㻜㻌

㻙

㻝

㻚

㻜

㻌

㻝㻚㻜㻜㻌㻝㻚㻝㻜㻌㻝㻚㻞㻜㻌㻝㻚㻟㻜㻌

䌖㼡㻟㻛䌖

䌖㼡

㻟

㻛䌖䃖

㻝

㻻

㼤

㻻

㼦

㼀㼕

㻻

㼤

䌖㼡

㻟

㻛䌖䃖

㻝

㼏㻛㼍

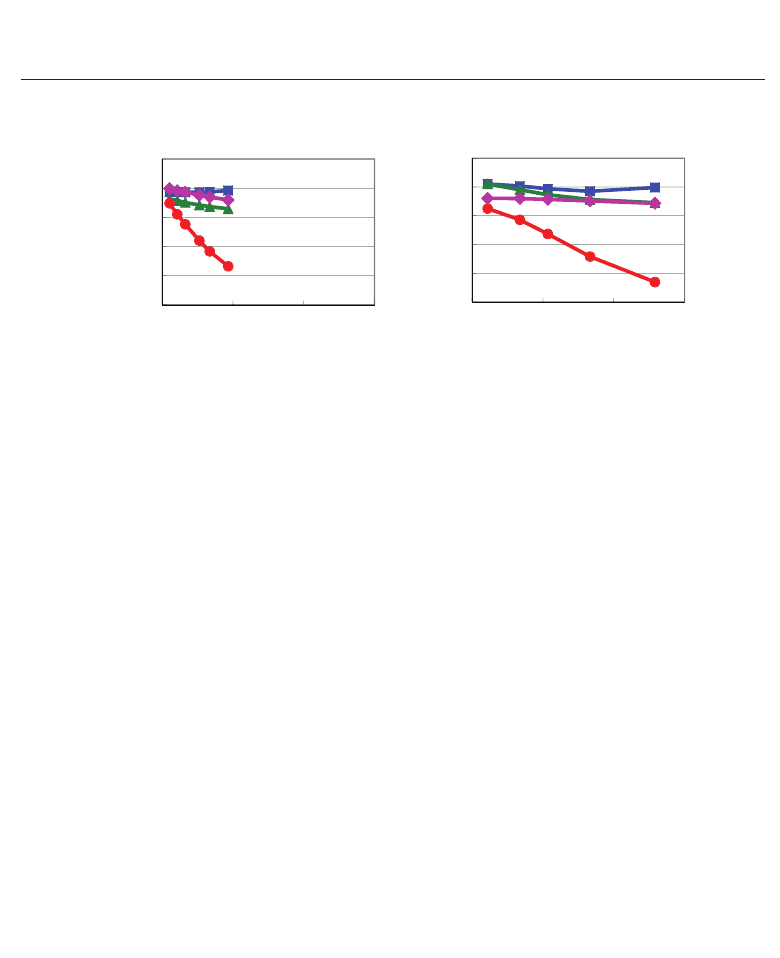
Fig. 11. Evaluated values of ∂u

(k)/∂η

as a function of c /a ratios: (a) SrT iO

and

(b) BaTiO

(Furuta & Miura, 2010).

the other hand, Figs. 11(a) and 11(b) show the ∂u

(k)/∂η

values in SrTiO

and BaTiO

respectively; η

is deﬁned as η

≡ (a − a

)/a

,wherea

denotes the a lattice parameter

with fully optimized structure. The absolute values of ∂u

(k)/∂η

, especially for Ti, O

,and

, are different in between SrTiO

and BaTiO

. As a result, the quantitative differences in

and e

in between SrTiO

and BaTiO

are due to the differences in the contribution of

the ∂u

(k)/∂η

values. In the following, the author would like to discuss the reasons of the

quantitative differences in e

and e

in between SrTiO

and BaTiO

Figure 12(a) shows the difference between the A–O

distance (R

A−O

)andthesumofr

and r

+ r

) on the (100) plane as a function of the ratio c/a, where the values of the

ionic radii are deﬁned as Shannon’s ones (Shannon, 1976). Note that R

A−O

is smaller than

+ r

in both SrTiO

and BaTiO

. However, the difference in absolute value between R

A−O

and r

+ r

in SrTiO

is much smaller than the difference in BaTiO

for 1.00  c/a  1.10.

This result suggests that the Sr–O

Coulomb repulsion on the (100) plane in SrTiO

is much

smaller than the Ba–O

Coulomb repulsion in BaTiO

and that therefore Sr and O

ions of

SrTiO

can be displaced more easily along the [001] axis than Ba and O

ions of BaTiO

.This

would be a reason why the absolute values of ∂u

(k)/∂η

of Sr and O

ions in SrTiO

are

larger than those of Ba and O

ions in BaTiO

. Figure 12(b) shows the difference between the

Ti–O

distance (R

Ti−O

)andr

+ r

along the [001] axis as a function of the ratio c/a.Note

that R

Ti−O

is smaller than r

+ r

in both SrTiO

and BaTiO

. However, the difference in

absolute value between R

Ti−O

and r

+ r

in SrTiO

is smaller than the difference in BaTiO

for 1.00  c/a  1.10. This result suggests that the Ti–O

Coulomb repulsion along the [001]

axis in SrTiO

is smaller than that in BaTiO

and that therefore the Ti ion of SrTiO

can be

displaced more easily along the [001] axis than that of BaTiO

. This would be a reason why

the absolute values of ∂ u

(k)/∂η

of Ti and O

ions in SrTiO

are larger than that in BaTiO

In the following, the author discusses the relationship between ∂u

(Ti)/∂η

and the ratio

c/a in detail. Figure 13(a) shows the properties of the diffrences in the total energy (ΔE

total

)

as a function of u

. In this ﬁgure, the properties of SrTiO

with c/a = 1.021 (η = 0.011),

SrTiO

with c/a = 1.093 (η = 0.053) and BaTiO

with c/a = 1.022 as a reference, are shown.

Calculations of E

total

were performed with the ﬁxed crystal structures of previously optimized

structures except Ti ions. Figure 13(b) shows illustrations of ΔE

total

curves with deviations at

the minimum points of the ΔE

total

values, corresponding to the ΔE

total

curves of SrTiO

Fig. 13(a). Clearly, as η

becomes smaller, the deviated value at the minimum point of the

405

First-Principles Study of ABO

: Role of the

B–O Coulomb Repulsions for

Ferroelectricity and Piezoelectricity

12 Ferroelectrics

㻻

㼦

㻾

㼀㼕㻙㻻㼦

㻾

㻭

㻙

㻻㼤

㻻

㼤

㼀㼕

㼇㻝㻜㻜㼉

㼇㻜㻝㻜㼉

㼇㻜㻜㻝㼉

㻔㻕

㻭

㻻㼤

㻜㻚㻜

㻜㻜

㻔㼍㻕㻔㼎㻕

㻾

㻭㻙㻻㼤

䇵㻔㼞

㻭

㻗㻌㼞

㻻㼤

㻕㻌㼢㻚㼟㻚㻌㼏㻛㼍㻌㻾

㼀㼕㻙㻻㼦

䇵㻔㼞

㼀㼕

㻗㻌㼞

㻻㼦

㻕㻌㼢㻚㼟㻚㻌㼏㻛㼍㻌

㻕

㻌

㻭㻌

㻔

㻿㼞㻌㼛㼞㻌㻮㼍

㻕

㻙㻜㻚㻟㻌

㻙㻜㻚㻞㻌

㻙㻜㻚㻝㻌

㻜㻚㻜

㻌

㼀

㼕㻙㻻㻟㻙㼞㼋㼀㼕㻻㻟㻔㻭㻕

㻙㻜㻚㻟㻌

㻙㻜㻚㻞㻌

㻙㻜㻚㻝㻌

㻜

㻚

㻜

㻌

㻭

㻙㻻㻝㻌㻙㼞㼋㻭㻻㻌㻔㻭㻕

㻭

㻙㻻㼤

䇵㻔㼞

㻭

㻗㻌㼞

㻻㼤

㻕㻌㻔䊅㻕㻌

㻿㼞㼀㼕㻻

㻟

㼀

㼕㻙㻻㼦

䇵㻔㼞

㼀㼕

㻗㻌㼞

㻻㼦

㻕㻌㻔䊅

㻕

㻿㼞㼀㼕㻻

㻟

㻮㼍㼀㼕㻻

㻟

㻙㻜㻚㻠㻌

㻝㻚㻜㻜㻌㻝㻚㻝㻜㻌㻝㻚㻞㻜㻌㻝㻚㻟㻜㻌

㻾㼋

㼀

㼏㻛㼍

㻙㻜㻚㻠㻌

㻝㻚㻜㻜㻌㻝㻚㻝㻜㻌㻝㻚㻞㻜㻌㻝㻚㻟㻜㻌

㻾㼋

㻭

㼏㻛㼍

㻾

㻭

㻮㼍㼀㼕㻻

㻟

㻾

㼀

Fig. 12. Evaluated values as a function of c /a ratios in optimized tetragonal SrT iO

and

BaTiO

: (a) difference between the A–O

distance (R

A−O

)andr

+ r

, and (b) difference

between the Ti–O

distance (R

Ti−O

)andr

+ r

, as a function of the ratio c/a. R

A−O

and

Ti−O

in ATiO

are also illustrated; all the ionic radii are much larger, and A and Ti ions are

displaced along the [001] axis in real ATiO

(Furuta & Miura, 2010).

ΔE

total

values becomes smaller, i.e., the Ti ion can be displaced more favourably. On the other

hand, as shown in Fig. 10(a), the absolute value of ∂u

(Ti)/∂η

becomes larger as η

becomes

smaller. Therefore, the Ti ion can be displaced more favourably as the deviated value at the

minimum point of the ΔE

total

values becomes smaller.

Next, let us discuss quantitative properties of e

, especially the reason why e

in SrTiO

shows negative while positive in BaTiO

. Figure 14(a) shows the difference between the

Ti–O

distance (R

Ti−O

)andr

+ r

along the [100] axis as a function of the ratio c/a.Note

that R

Ti−O

is smaller than r

+ r

in both SrTiO

and BaTiO

. However, the difference in

absolute value between R

Ti−O

and r

+ r

in SrTiO

is larger than that in BaT iO

, i.e., R

Ti−O

in SrTiO

is smaller than R

Ti−O

in BaTiO

. This result suggests that the Ti–O

Coulomb

repulsion along the [100] axis in SrTiO

is larger than that in BaT iO

and that therefore Ti and

ions of SrTiO

can be displaced along the [001] axis more easily than those of BaTiO

as discussed in previous subsection. This would be a reason why the absolute values of

∂u

(k)/∂η

of Ti and O

ions in SrTiO

are larger than those in BaTiO

. Therefore, each

㼂㻕

㻜㻚㻜㻜㻠㻌

㻜㻚㻜㻜㻢㻌

㼂㻕

㻔㼍㻕㻔㼎㻕

䏓㻱

㼠㼛㼠㼍㼘

㼢㻚㼟㻚㻌䏓㼡

㼀㼕

㼂㻕

㻿㼞㼀㼕㻻

㻟

㻔䃖

㻟

㻩㻌㻜㻚㻜㻝㻝㻕

㻮㼍㼀㼕㻻

㻟

㼡㼚㼕㼠㻕

䏓㻱

㼠㼛㼠㼍㼘

㼢㻚㼟㻚㻌䏓㼡

㻟

㻔㼀㼕㻕䏓㻱

㼠㼛㼠㼍㼘

㼢㻚㼟㻚㻌䏓㼡

㻟

㻔㼀㼕㻕

㻙㻜㻚㻜㻜㻢㻌

䏓㻱㼠㼛㼠㻔㼑

㻙㻜㻚㻜㻜㻢㻌

㻙㻜㻚㻜㻜㻠㻌

㻙㻜㻚㻜㻜㻞㻌

㻜㻚㻜㻜㻜㻌

㻚㻌

䏓㻱㼠㼛㼠㻔

䏓㻱

㼠㼛㼠㼍㼘

㻔㼑

㻜㻌

䏓㻱

㼠㼛㼠㼍㼘

㻔㼍㼞㼎㻚㻌

㻿㼞㼀㼕㻻

㻟

㻔䃖

㻟

㻩㻌㻜㻚㻜㻡㻟㻕

㻚㻌

㼡㼋㼀㼕㻌㻔㻭㻕

㻚㻌㻚㻌㻚㻌㻚㻌

㼡㼋㼀㼕㻌㻔㻭㻕

㻌

䏓㼡

㻟

㻔㼀㼕㻌㻕㻌㻌㻔䊅㻕

䏓㼡

㻟

㻔㼀㼕㻌㻕㻌㻌㻔㼍㼞㼎㻚㻌㼡㼚㼕㼠㻕

406

Ferroelectrics - Characterization and Modeling

First-principles Study of ABO

: Role of the B–O Coulomb Repulsions for Ferroelectricity and Piezoelectricity 13

㼂㻕

㻜㻜㻜㻞

㻜㻚㻜㻜㻠㻌

㻜㻚㻜㻜㻢㻌

㼑

㼂㻕

㻔㼍㻕㻔㼎㻕

䏓㻱

㼠㼛㼠㼍㼘

㼢㻚㼟㻚㻌䏓㼡

㼀㼕

㼂㻕

㻿㼞㼀㼕㻻

㻟

㻔䃖

㻟

㻩㻌㻜㻚㻜㻝㻝㻕

㻮㼍㼀㼕㻻

㻟

㼡㼚㼕㼠㻕

䏓㻱

㼠㼛㼠㼍㼘

㼢㻚㼟㻚㻌䏓㼡

㻟

㻔㼀㼕㻕䏓㻱

㼠㼛㼠㼍㼘

㼢㻚㼟㻚㻌䏓㼡

㻟

㻔㼀㼕㻕

㻙㻜㻚㻜㻜㻢㻌

㻜㻜

䏓㻱㼠㼛㼠㻔㼑

㻙㻜㻚㻜㻜㻢㻌

㻙㻜㻚㻜㻜㻠㻌

㻙㻜㻚㻜㻜㻞㻌

㻜㻚㻜㻜㻜㻌

㻜

㻚

㻜㻜㻞

㻌

㻜㻜

㻜㻝

㻜㻞

㻜㻟

䏓㻱㼠㼛㼠㻔

㼑

䏓㻱

㼠㼛㼠㼍㼘

㻔㼑

㻜

㻜㻌

䏓㻱

㼠㼛㼠㼍㼘

㻔㼍㼞㼎㻚㻌

㻿㼞㼀㼕㻻

㻟

㻔䃖

㻟

㻩㻌㻜㻚㻜㻡㻟㻕

㻜

㻚

㻜

㻌

㼡㼋㼀㼕㻌㻔㻭㻕

㻜

㻚

㻜

㻌

㻜

㻚

㻝

㻌

㻜

㻚

㻞

㻌

㻜

㻚

㻟

㻌

㼡㼋㼀㼕㻌㻔㻭㻕

㻜

㻌

䏓㼡

㻟

㻔㼀㼕㻌㻕㻌㻌㻔䊅㻕

䏓㼡

㻟

㻔㼀㼕㻌㻕㻌㻌㻔㼍㼞㼎㻚㻌㼡㼚㼕㼠㻕

Fig. 13. (a) ΔE

total

as a function of u

in tetragonal SrTiO

and BaTiO

. (b) Illustration of the

ΔE

total

curves in tetragonal SrTiO

(η = 0.011) and SrTiO

(η = 0.053) with deviations at the

minimum point of ΔE

total

absolute value of Z

∗

× ∂u

(Ti)/∂η

( < 0) and Z

∗

× ∂u

)/∂η

( > 0) in SrTiO

is larger

than that in BaT iO

. Figure 14(b) shows the difference between the A–O

distance (R

A−O

)

and r

+ r

on the (001) plane as a function of the ratio c/a.NotethatR

A−O

is smaller

than r

+ r

in both SrTiO

and BaTiO

. However, the difference in absolute value between

A−O

and r

+ r

in BaTiO

is larger than that in SrTiO

. This result suggests that the

Ba–O

Coulomb repulsion on the (001) plane in BaTiO

is larger than that in SrTiO

and

that therefore O

ion of BaTiO

can be displaced along the [001] axis more easily than that of

SrTiO

, as discussed in previous subsection. This would be a reason why the absolute value of

∂u

(k)/∂η

of O

ion in BaTiO

is larger than that in SrTiO

. Therefore, the absolute value of

∗

×∂u

)/∂η

( > 0) in BaTiO

is larger than that in SrT iO

. Finally, as a result, the above

investigations suggest that the signature of e

in SrTiO

or BaTiO

is closely related to the

difference in absolute values between Z

∗

× ∂u

(Ti)/∂η

and the sum of Z

∗

× ∂u

)/∂η

and Z

∗

×∂u

)/∂η

4. Summary

Using a ﬁrst-principles calculation with optimized structures, the author has investigated

the role of the Coulomb repulsions between Ti 3s and 3p states and O 2s and 2p states

in ferroelectric BaTiO

. It has been found that the Coulomb repulsions between Ti 3s

and 3p

x (y)

states and O

x (y)

2s and 2p

x (y)

states are closely related to the appearance of

Ti ion displacement in tetragonal BaTiO

. This mechanism seems to be consistent with

the appearance of Ti ion displacement in rhombohedral BaTiO

. The present investigation

suggests that the Coulomb repulsions between Ti 3s and 3p states and O 2p states have

an important role in ferroelectricity. In addition to this suggestion, the author believes that

the present investigation will show a g uideline for the choice of PPs when ﬁrst-principles

calculations with PP methods are performed. The author has also investigated the ferroelectric

and piezoelectric properties of SrTiO

and BaTiO

with in-plane compressive tetragonal

structures using a ﬁrst-principles calculation. It has been found that the ferroelectric structure

even in SrTiO

appears with in-plane compressive structures. The piezoelectric constant e

drastically increases in SrTiO

rather than that in BaTiO

as the tetragonal ratio c/a (> 1) is

407

First-Principles Study of ABO

: Role of the

B–O Coulomb Repulsions for

Ferroelectricity and Piezoelectricity

14 Ferroelectrics

㻻

㼤

㼀㼕

㻻

㼦

㻾

㻭㻙㻻㼦

㻻

㼤

㼀㼕

㼇㻝㻜㻜㼉

㼇㻜㻝㻜㼉

㼇㻜㻜㻝㼉

㻭㻔㻿㼞㼛㼞㻮㼍㻕

㻾

㼀㼕㻙㻻㼤

㻙㻜㻚㻥㻌

㻜㻚㻜㻌

㻭

㻕

㻔㼍㻕㻔㼎㻕

䊅

㻕㻌

㻾

㼀㼕㻙㻻㼤

䇵㻔㼞

㼀㼕

㻗㻌㼞

㻻㼤

㻕㻌㼢㻚㼟㻚㻌㼏㻛㼍㻌

㻮㼀㼕㻻

㻾

㻭㻙㻻㼦

䇵㻔㼞

㻭

㻗㻌㼞

㻻㼦

㻕㻌㼢㻚㼟㻚㻌㼏㻛㼍㻌

䊅

㻕㻌

㻿㼀㼕㻻

㻭

㻌

㻔㻿㼞

㻌

㼛㼞

㻌

㻮㼍㻕

㻝㻟

㻙㻝㻚㻞㻌

㻙㻝㻚㻝㻌

㻙㻝㻚㻜㻌

㻾

㼋㻭㻙㻻㻟㻌㻙㼞㼋㻭㻻㻌㻔㻭㻕

㻙㻜㻚㻟㻌

㻙㻜㻚㻞㻌

㻙㻜㻚㻝㻌

㻾

㼋㼀㼕㻙㻻㻝㻙㼞㼋㼀㼕㻻㻝㻔

㻭

㻾

㼀㼕㻙㻻㼤

䇵㻔㼞

㼀㼕

㻗㻌㼞

㻻㼤

㻕㻌㻔

䊅

㻿㼞㼀㼕㻻

㻟

㻮

㼍

㼀㼕㻻

㻟

㻾

㻭㻙㻻㼦

䇵㻔㼞

㻭

㻗㻌㼞

㻻㼦

㻕㻌㻔

䊅

㻿

㼞

㼀㼕㻻

㻟

㻮㼍㼀㼕㻻

㻟

㻙

㻝

㻚

㻟

㻌

㻝㻚㻜㻜㻌㻝㻚㻝㻜㻌㻝㻚㻞㻜㻌㻝㻚㻟㻜㻌

㻾

㼏㻛㼍

㻙㻜㻚㻠㻌

㻝㻚㻜㻜㻌㻝㻚㻝㻜㻌㻝㻚㻞㻜㻌㻝㻚㻟㻜㻌

㻾

㼏㻛㼍

㻾

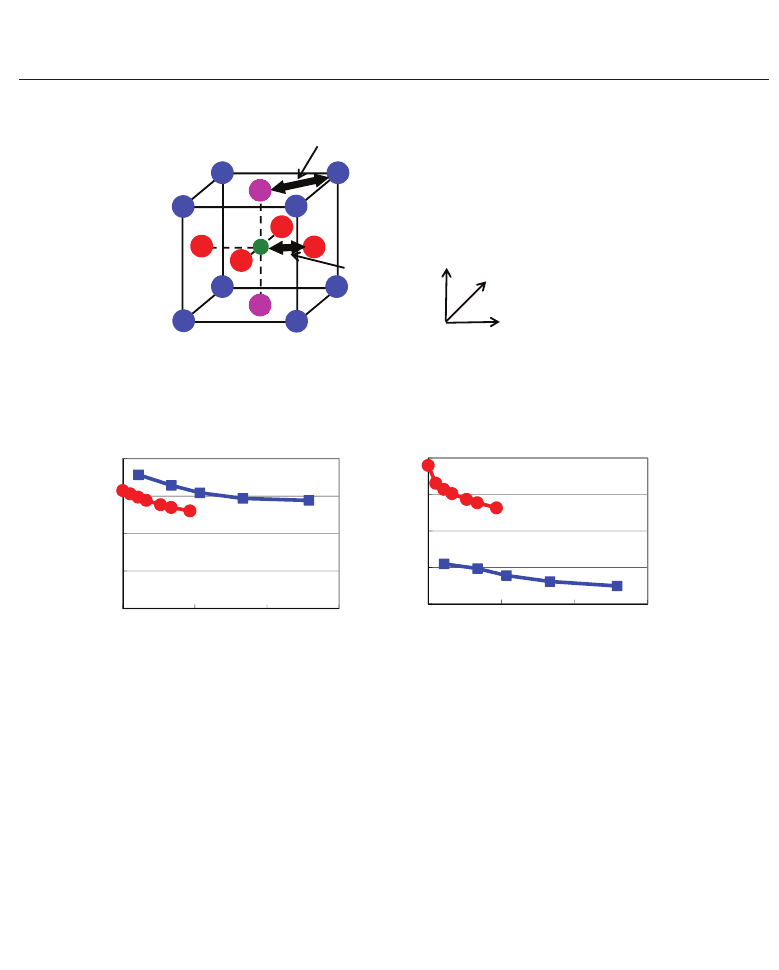
Fig. 14. Evaluated values as a function of c /a ratios in optimized tetragonal SrT iO

and

BaTiO

: (a) difference between the Ti–O

distance (R

Ti−O

)andr

+ r

, as a function of the

ratio c/a , and (b) difference between the A–O

distance (R

A−O

)andr

+ r

. R

Ti−O

and

A−O

in ATiO

are also illustrated (Furuta & Miura, 2010).

close to 1. On the other hand, e

shows negative in SrTiO

while positive in BaTiO

,although

the changes in their absolute values are very small. The author has found that these properties

of e

and e

in SrTiO

and BaTiO

are closely related to the ionic distances.

5. Acknowledgements

The author thanks Professor H. Funakubo, Professor M. Azuma, M. Kubota and T. Furuta

for useful discussion. The present work was partly supported by the Elements Science and

Technology Project from the Ministry of Education, Culture, Sports, Science and Technology,

Japan. Calculations for the present work were partly performed by the supercomputing grid

cluster machine “TSUBAME" in Tokyo Institute of Technology.

6. References

Ahart, M., Somayazulu, M., Cohen, R. E., Ganesh, P., Dera, P., Mao, H., Hemley, R.,

Ren, Y., Liermann, P. & Wu, Z. (2008). Origin of morphotropic phase boundaries in

408

Ferroelectrics - Characterization and Modeling