Lallart M. Ferroelectrics: Characterization and Modeling
Подождите немного. Документ загружается.


Intrinsic Interface Coupling in Ferroelectric Heterostructures and Superlattices
379
In eq. (22), the total free energy density of the ferroelectric layer
1
F is given by
1
2
/2
24
111
1
0
d
242d
L
p
F
pp p
Edx
x
αβκ
=++−
, (23)
whereas the total free energy densities of the paraelectric layer
2
f
is
1
2
/2
2
22
2
/2
d
d
22d
L
L
q
Fq qEx
x
ακ
=+−
, (24)
respectively. In eqs. (23) and (24), p and q are the order parameters of the ferroelectric layer
and paraelectric layer, respectively.
E
denotes the external electric field.
The coupling energy at the interface between the ferroelectric- and dielectric-layers is as
shown in eq. (3). In this case, the boundary conditions at the interface (x = L
1
/2) are
described by
()
()
ii
1
ii
2
d
,
d
d
.
d
p
p
q
x
q
pq
x
λ
κ
λ
κ
=− −
=−
(25)
3.1 Polarization modulation profiles
We first look at the polarization modulation profiles of the ferroelectric/dielectric
superlattice under the absence of an external electric field 0E = (Chew et al., 2009). The
polarization profiles of p and q for the ferroelectric and dielectric layers, respectively, can be
obtained using the Euler-Lagrange equation. For the dielectric layer, the Euler-Lagrange
equation is
2
22
2
d
d
q
q
x
κα
=
, (26)
and
()qx can be obtained as
c2
() cosh
2
L
qx q K x
=−
, (27)
and at the interface, we have
22
c
cosh
2
i
KL
qq=
, (28)
where
c
q is the q value at d/d 0qx= .
By integrating once, the Euler-Lagrange equation of the ferroelectric layer is
()()
2
22 44
11 1
cc
d
2d 2 4
p
p
ppp
x
κα β
=−+−
, (29)
Ferroelectrics - Characterization and Modeling
380
where
c
p
is the p value at d/d 0px= . In this case,
c
p
is the maximum value of p at 0x = .
Using
()
c
() sin
p
x
p
x
θ
= and
2
b11
/p
αβ
=− , eq. (29) becomes
1i
1
2
22
1
/2
d
d
(1 )
1sin
x
L
x
k
k
θ
θ
αθ
κ
θ
−
−
=
+
−
, (30)
where
(,)Fk
θ
and
i
(,)Fk
θ
are the elliptic integral of the first kind with the elliptic modulus
k given by
2
2
c
22
bc
2
p
k
pp
=
−
. (31)
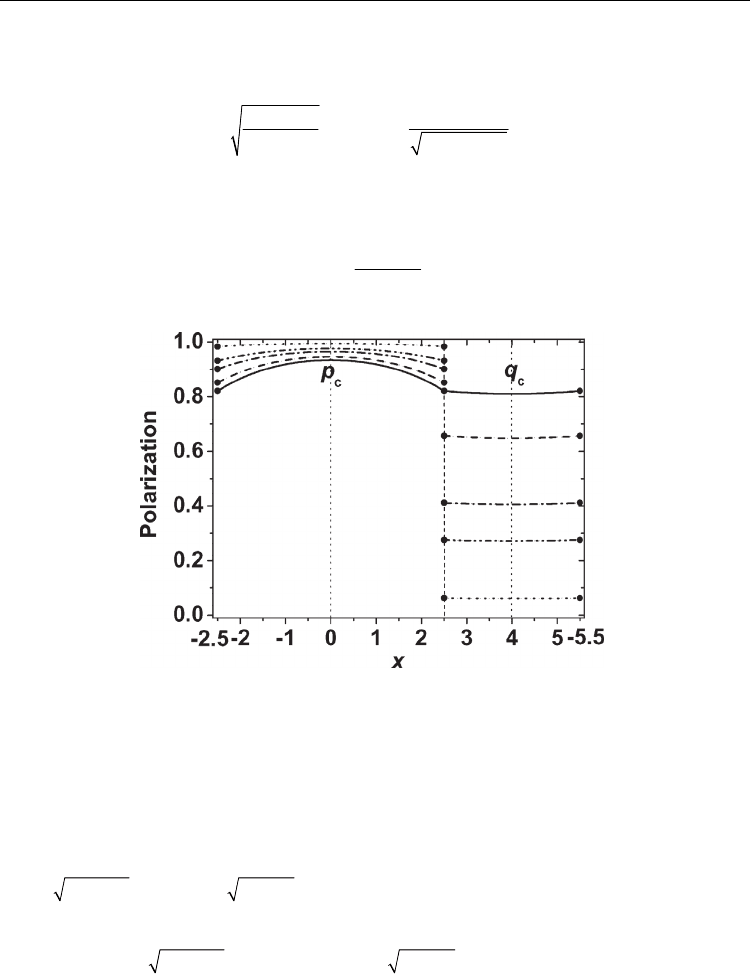
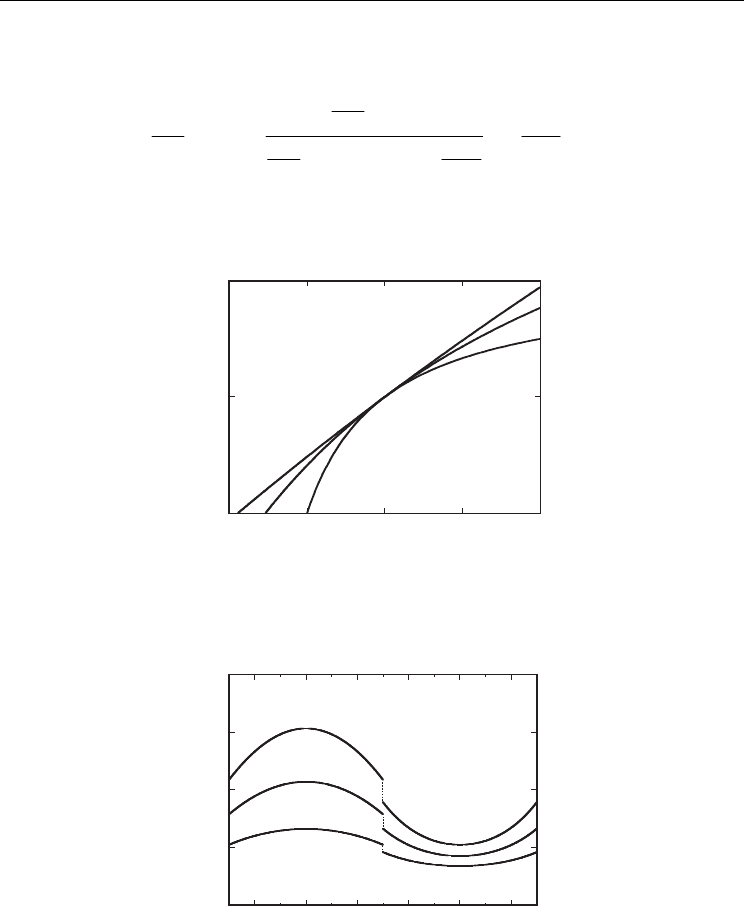
Fig. 4. Spatial dependence of polarization for a superlattice with
1
5L = and
2
3L = for
various
1
λ
−
. The parameters adopted for the calculation are:
1
1
α
=− ,
2
0.1
α
= ,
1
1
β
= ,
2
1
β
= ,
1
4
κ
= and
2
9
κ
= . In the curves, the values for
1
λ
−
are: 100 (dot), 16 (dash-dot-dot),
8 (dash-dot), 2 (dash), and 0 (solid). Dotted circles represent the interface polarizations
(Chew et al., 2009).
Let us discuss the polarization modulation profiles in a ferroelectric/dielectric superlattice
using the explicit expressions. The characteristic lengths of polarization modulations in the
ferroelectric layer near the transition point and the dielectric layer are given by
1
111
/K
κα
−
=− and
1
222
/K
κα
−
= , respectively. Figure 4 illustrates an example of
1
λ
−
dependence of polarization modulation profiles. It is seen that the modulation of the
polarization is obvious in the ferroelectric layer, but not in the dielectric layer. This is
because
111
/2 / 2L
κα
>− = and
222
/2 / 0.95L
κα
<≈. For a loosely coupled
superlattice of
1
100
λ
−
= (dot lines), only a weak polarization is induced in the dielectric
layer. As the strength of the interface coupling
λ
increases, the polarization near the
interface of the ferroelectric layer is slightly suppressed, whereas the induced-polarization
of the soft dielectric layer increases.

Intrinsic Interface Coupling in Ferroelectric Heterostructures and Superlattices
381
3.2 Phase transitions
Using the explicit expressions (as obtained in Sect. 3.1), the average energy density of the
superlattice F (eq. (22)) can be written in terms of p
c
and q
c
as (Chew et al., 2009)
224 22 2
11 1 1 1
ccc ciccc
2
2
sin ,
2422 2
1
LD
FJppppCpqq
L
k
ακ α β λ
θ
−
=+++−+
+
(32)
where
()
i
22
i
22
2
22
22
222
/2
cosh sin ,
2
sinh cosh ,
22
cos 1 sin ,
KL
C
KL
DKL
Jkd
θ
π
λθ
ακ
λ
θθθ
=⋅
=+
=−
(33)
with
()
1
iic
sin /
p
p
θ
−
= . By utilizing
()
22 2
b
/2
c
kp p≈ and
1
K (see eq. (12)) near the transition
point, F becomes
()
24 2
ccccc
2
,
22
AD
FpOpCpqq
L
=+−+
(34)
where
11
2
11
11
sin cos
22
KL
AKL
ακ
λ
−
=− +
, (35)
and O(p
c
4
) indicates the higher order terms of p
c
4
.
From the equilibrium condition for q
c
, dF/dq
c
= 0, the condition of the transition point can
be obtained as A - C
2
/D = 0, i.e.,
11
2
11
11
sin cos 0
22
KL
KL R
ακ
−
−+=
, (36)
where
22
22
,tanh
2
rKL
Rr
r
λ
ακ
λ
==
+
. (37)
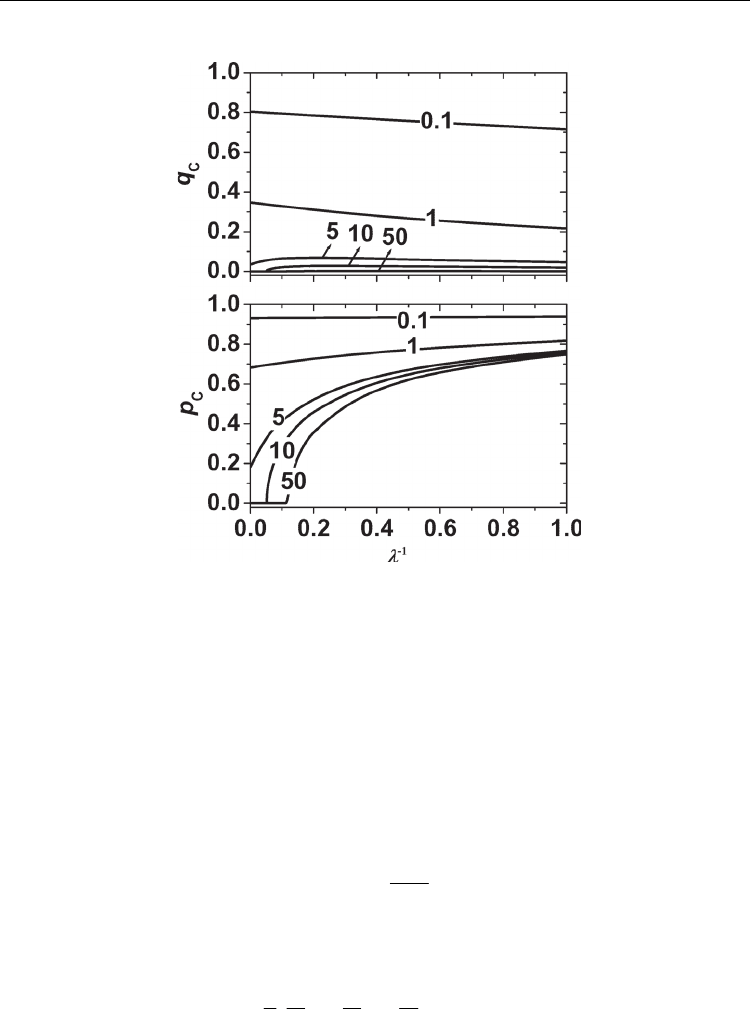
In Fig. 5, we show the dependence of
c
p
and
c
q
on
1
λ
−
for different dielectric stiffness
2
α
.
For a superlattice with a soft dielectric layer
2
0.1
α
=
and 1,
c
p
remains almost the same as
the bulk polarization
cb
~
p
p
for all
1
λ
−
. For the case with
2
5
α
=
,
c
p
is suppressed near the
strong coupling regime
1
~0
λ
−
. If the dielectric layer is very rigid (
2
α
= 10 and 50), we
found that
c
p
is strongly suppressed with increasing interface coupling and
c
q
remains
very weak. It is seen that the polarizations of the superlattices with rigid dielectric layers are
completely disappeared at
1
λ
−
≈
0.0514 and 0.1189, respectively. These transition points
can be obtained using eq. (36).
Ferroelectrics - Characterization and Modeling
382
Fig. 5. p
c
and q
c
as a function of
1
λ
−
for various
2
α
, where
2
α
is 0.1, 1, 5, 10, and 50. The
other parameters are the same as Fig. 4 (Chew et al., 2009).
As the temperature increases, the ferroelectric layer can be in the ferroelectric state or in the
paraelectric state. Phase transition may or may not take place, depending on the model
parameters. Let us examine the stability of superlattice in the paraelectric state by taking
into account the polarization profile to appear in the ferroelectric state. Instead of the exact
solutions obtained from the Euler-Lagrange equations, which are in term of the Jacobi
Elliptic Functions, we use (Ishibashi & Iwata, 2007)
1
cos
c
p
pKx= , (38)
thus p
i
becomes
11
cos
2
ic
KL
pp=
. (39)
The Euler-Lagrange equation for q is given by eq. (26), which gives q(x) as expressed in eq.
(27). Substitution of eqs. (27) and (38) into eq. (22), F becomes
242
112
ccccc
2
,
242
aba
Fppqcpq
L
=++−
(40)
where

Intrinsic Interface Coupling in Ferroelectric Heterostructures and Superlattices
383
()
2
22
111 11
11111 11
1
1 1 11 11
1
11
2
22222 22
2
2
11 22
1
sin cos ,
42
3sin sin2
,
44 8
sinh cosh cosh ,
22 2
cos cosh .
22
KKL
aKL KL
K
LKL KL
b
KK
KL KL KL
a
K
KL KL
c
ακ
ακ λ
β
α
λ
λ
−
=+ + +
=+ +
=+
=
(41)
Similarly, from the equilibrium condition for q
c
, dF/dq
c
= 0, we find eq. (40) can be reduced
to a more simple form as
*
24
11
cc
2
24
ab
Fpp
L
=+
, (42)
where
2
*2 2
1111 11
1111 11
11
sin cos ,
42
LKKL
aK KLR
KL
ακ
ακ
−
=++ +
(43)
where
(,)Rr
λ
is given by eq. (37). r is a function of
2
α
,
2
κ
and
2
L . The transitions of the
superlattice from a paraelectric phase to a ferroelectric state occurs when
*
1
0a =
. Note here
that
*
1
a
consists of the physical parameters from both the ferroelectric and dielectric layers.
It is seen that the influence of the dielectric layer via
λ
becomes stronger with increasing
2
α
,
2
κ
and
2
L . However, the influence is limited at most to
max 2 2
r
ακ
=
. Let us look at
*
1
a
in more detail. By taking
1
*
1
1
0
Kk
a
K
=
∂
=
∂
, we obtain the wave number k. It is qualitatively
Fig. 6. The dependence of the wave number k for various R/L
1
when κ
1
= 1 and L
1
= 1/2. The
curves show the cases 1) R/L
1
= 0, 2) R/L
1
= 2, 3) R/L
1
= 20, 4) R/L
1
= 200 and 5) R/L
1
=∞.
Dotted lines denote the transition point of each case (Ishibashi & Iwata, 2007).

Ferroelectrics - Characterization and Modeling
384
obvious that k is small, implying a flat polarization profile, when the contribution from the
dielectric layer R, is small, while
2
kL approaches π, implying a very weak interface
polarization in the ferroelectric layer, when R is extremely large. The dependence of the
wave number k on
1
α
for various
1
/RLis illustrated in Fig. 6.
3.3 Dielectric susceptibilities
In this section, we will discuss the dielectric susceptibility of the superlattice in the
paraelectric phase (Chew et al., 2008). Since p(x) = q(x) = 0 in the paraelectric phase (if 0E = ),
the modulated polarizations, p(x) and q(x), are the polarizations induced by the electric field
E. The contribution from the higher-order term
4
1
/4p
β
is neglected because we consider
only the paraelectric phase. By solving the Euler-Lagrange equations, we found
2
11
2
2
22
2
d
,
d
d
,
d
p
p
E
x
q
qE
x
ακ
ακ
−=
−=
(44)
with the condition that F (eq. (22)) including the interface energy (eq. (3)) takes the
minimum value. Note that in the present system, the ferroelectric transition point
c
α
is
negative. Thus, one must consider both cases
1
0
α
≥ and
1
0
α
< in the study of the dielectric
susceptibility even in the paraelectric phase. In the present system, the dielectric
susceptibility
χ
is defined as
1
1
/2 /2
0/2
2
dd
LL
L
p
xqx
LE
χ
=+
. (45)
3.3.1 Case
1
0
α
≥
For the case of
1
0
α
≥ , the exact solutions are
c1
1
c2
2
cosh ,
cosh ,
2
E
ppE Kx
LE
qqE Kx
α
α
=+
=−+
(46)
and
11
ic
1
22
ic
2
cosh ,
2
cosh .
2
KL E
ppE
KL E
qqE
α
α
=+
=+
(47)
In this case,
111
/K
ακ
= and
2
K is given by eq. (14). By utilizing eqs. (46) and (47), we can
express F in terms of
c
p
and
c
q as
Intrinsic Interface Coupling in Ferroelectric Heterostructures and Superlattices
385
22 2
12
cccc1c2c
2
22
aa
F
pq
c
pq
d
p
d
q
E
L
=+−−−
, (48)
where
2
111
111
1
2
22
222
2
11 22
11
1
12
22
2
12
sinh cosh ,
22
2
sinh cosh ,
22
cosh cosh ,
22
11
cosh ,
2
11
cosh .
2
KL
aKL
K
KL
aKL
K
KL KL
c
KL
d
KL
d
α
λ
α
λ
λ
λ
αα
λ
αα
=+
=+
=
=− −
=−
(49)
Using the equilibrium conditions
cc
//0Fp Fq∂∂=∂∂=
, we find
211
c22
22 12
11
cosh sinh ,
22
KL
pKL
aA K
λα
αα
−
=−
(50)
and
122
c11
21 12
11
cosh sinh ,
22
KL
qKL
aA K
λα
αα
=−
(51)
where
2
1
2
c
Aa
a
=−
. (52)
Based on eq. (45), the dielectric susceptibility for the present case is
cc
11 1 22 2
112 2
22
sinh sinh
22
pq
KL L KL L
KL L KL L
χ
αα
=+++. (53)
3.3.2 Case
1
0
α
<
In this case, the exact solutions of eq. (44) are
c1
1
c2
2
cos ,
cosh ,
2
E
ppE Kx
LE
qqE Kx
α
α
=+
=−+
(54)
Ferroelectrics - Characterization and Modeling
386
where
1
K and
2
K are given by eq. (12) and (14), respectively. Thus, we have
11
ic
1
22
ic
2
cos ,
2
cosh .
2
KL E
ppE
KL E
qqE
α
α
=+
=+
(55)
Similarly, we find
22 2
12
cccc1c2c
2
22
aa
F
pq
c
pq
d
p
d
q
E
L
=+−−−
, (56)
where
2
111
111
1
2
222
222
2
11 22
11
1
12
22
2
12
sin cos ,
22
sinh cosh ,
22
cos cosh ,
22
11
cos ,
2
11
cosh ,
2
KL
aKL
K
KL
aKL
K
KL KL
c
KL
d
KL
d
α
λ
α
λ
λ
λ
αα
λ
αα
=+
=+
=
=− −
=−
(57)
and the the values of p
c
and q
c
become
211
c22
22 12
11
cos sinh ,
22
KL
pKL
aA K
λα
αα
−
=−
(58)
and
122
c11
21 12
11
cosh sin ,
22
KL
qKL
aA K
λα
αα
=−
(59)
with
2
1
2
c
Aa
a
=−
. (60)
Using eqs. (45), the dielectric susceptibility
χ
for the present case of
1
0
α
< is
cc
11 1 22 2
112 2
22
sin sinh
22
pq
KL L KL L
KL L KL L
χ
αα
=++ +
, (61)
Intrinsic Interface Coupling in Ferroelectric Heterostructures and Superlattices
387
where the phase transition point is given by
2
12
/0Aa c a=− =. Using
2
12
/0Aa c a=− =,
the condition of the transition point is
2
22
2
1112
11
2
222
1
22
2
sin
2
sin cos 0.
22
sin cosh
22
KL
KLK
KL
KL
K
KL
K
α
λ
α
α
λ
+=
+
(62)
It is interesting to note here that the transition temperature
1
α
can be determined using eq.
(62), which is exactly the same as eq. (43) (Ishibashi & Iwata, 2007).
Fig. 7. Reciprocal susceptibility as a function of
2
α
. The parameter values are adopted as
1L =
,
12
1/2LL==
,
12
1
κκ
==
,
2
1
α
=
, for cases of: (1) 0
λ
= , (2) 0.3
λ
= , (3) 3
λ
=
(Chew et al., 2008).
Fig. 8. Spatial dependence of polarization for a superlattice with
12
3LL==. The parameters
adopted for the calculation are:
12
1
κκ
==,
2
1
α
= ,3
λ
= , for cases of (1)
1
0.1
α
=− , (2)
1
0
α
= , (3)
1
0.2
α
= (Chew et al., 2008).
In Fig. 7, we show the reciprocal susceptibility
1/
χ
in various parameter values. It is found
that the average susceptibility diverges at the transition temperature obtained from eq. (62).
0
1
-1 0 1 2
1/
χ
α
1
1
2
3
0
2
4
6
8
-1 0 1 2 3 4
x
p
q
1
2
3
Polarizatio
n

Ferroelectrics - Characterization and Modeling
388
The result indicates that the second-order phase transition is possible in our model of the
superlattice structure. It is seen that the susceptibility is continuous at
1
0
α
= , though the
susceptibility is divided into two different functions at
1
0
α
= . Taking the limit of
1
0
α
=±
from both the positive and negative sides, the explicit expression for the susceptibility at
1
0
α
=
is
2
22
232
12 1 1 12
21222
cosh
12
2
2212sinh
KL
LL L L LK
LKL
χ
αλκα
+
=+++
, (63)
implying that the susceptibility is always continuous at
1
0
α
= . It is worthwhile to look at
the field-induced polarization profile at
1
0
α
= because
1
K becomes zero at
1
0
α
= . By
taking the limit of
1
0
α
=± from both the positive and negative sides for the polarization p,
the expressions for the polarization profiles in
()
p
x and ()qx can be explicitly expressed as
()
()
2
22
22
121
1
12222
cosh
2
4
82sinh
KL
EELEKL E
px L x
KL
κλα α
=−++ +
,
(64)
and
()
22
21
2
222 2
cosh
2
cosh
sinh 2
KL
EK L
LE
qx K x
KL
αα
=−+
(65)
Equation (64) depicts the polarization profile
()
p
x that exhibits a parabolic modulation at
1
0
α
= , as shown in Fig. 8. The polarization profile obtained near the transition point may
coincide with the polarization modulation pattern of the ferroelectric soft mode in the
paraelectric phase.
3.4 Application of model to epitaxial PbTiO
3
/SrTiO
3
superlattices
Let us extend the model to study the ferroelectric polarization of epitaxial PbTiO
3
/SrTiO
3
(PT/ST) superlattices grown on ST substrate and under a short-circuit condition, as
schematically shown in Fig. 9. Some key points from the previous sections are repeated here
for clarity of discussion.
In this study, we need to include the effects of interface, depolarization field and substrate-
induced strain in the model. By assuming that all spatial variation of polarization takes
place along the
z-direction, the Landau-Ginzburg free energy per unit area for one period of
the PT/ST superlattice can be expressed as (Chew et al.,
unpublished)
PT ST I
FF F F
=++
, (66)
where the free energy per unit area for the PT layer with thickness
PT
L is
2
2
**
0
,
246
11, 12,
,
2462
1
,
2
PT
mPT
PT PT PT PT
PT
L
PT PT
dPT
u
dp
Fppp
dz s s
epdz
αβγκ
−
=++++
+
−
(67)
