Lallart M. Ferroelectrics: Characterization and Modeling
Подождите немного. Документ загружается.


Self-Consistent Anharmonic Theory and Its Application to BaTiO
3
Crystal
329
()
()
,N,,,SQemu
S
S
S
,nn,n
321 ⋅⋅⋅==
−
αα
1/2
()
,QcVQH
Sn,nS
S
nn
SnnS
′
′
′
++=
a
2
2
1
.QBQAQH
S
SS
S
SS
S
Str
++=
242
2
1
()
.FQBQAQcV
FHHF
tr
S
SS
S
SS
n,nS
S
nn
Snn
trtr
+−−
+=
+−=
′
′
′
24
a
()
,Qc
S
S
nn
Snnnn
′
′′
+=−
axx
(2)
where
nn
′
a
means the interatomic distance in equilibrium state and
n
u
denotes an atomic
displacement from the equilibrium position. The displacement
α
,n
u
in the αdirection is
expanded by using the eigenfunctions
()
S
,n
e
α
of a dynamical matrix as
(3)
where
S
Q
are the normal coordinates. The interatomic distance is represented by
(4)
where c
S
(nn’)
are defined by using the the direction cosine,
α
,nn
′
, of the interatomic distance
vector as (α=x,y,z)
(5)
Then, Hamiltonian is rewritten in terms of the normal coordinates
S
Q
as (Y. Aikawa & K.
Fujii, 1993)
(6)
The variational principle at finite temperature is applied to obtain thermal properties of the
crystal. In this method, an anharmonic oscillator with the fourth order term is adopted as a
trial Hamiltonian
tr
H
, (Y. Aikawa & K. Fujii, 2009)
(7)
The thermal average of a physical quantity
(
)
SS
Q,QX
is given by
() ()
()
()
()
B
B
Tr
exp k d d
exp k d d
,,
,
SS SS
SS tr SS
S
tr S S
S
XQ Q XQ Q
XQ Q H T Q Q
HT QQ
ρ
∞
−∞
∞
−∞
=
−
=
−
∏
∏
(8)
The free energy of the crystal is given by
(9)
The free energy
tr
F
of the trial system is also calculated by using the relation
trtr
ZTF lnk
B
−=
.
The partition function
tr
Z
is represented by using the variables
TQAy
SSS B
44
k≡
and
SSS
BTAp
B
k41≡
as:
,
nnnnnn
′′′
−+=−
uuaxx
() () ( )
()
.ememc
n
Sn
n
Sn,nn
nn
S
′
−
′
−
′
′
−=
α
αα
α
1/21/2
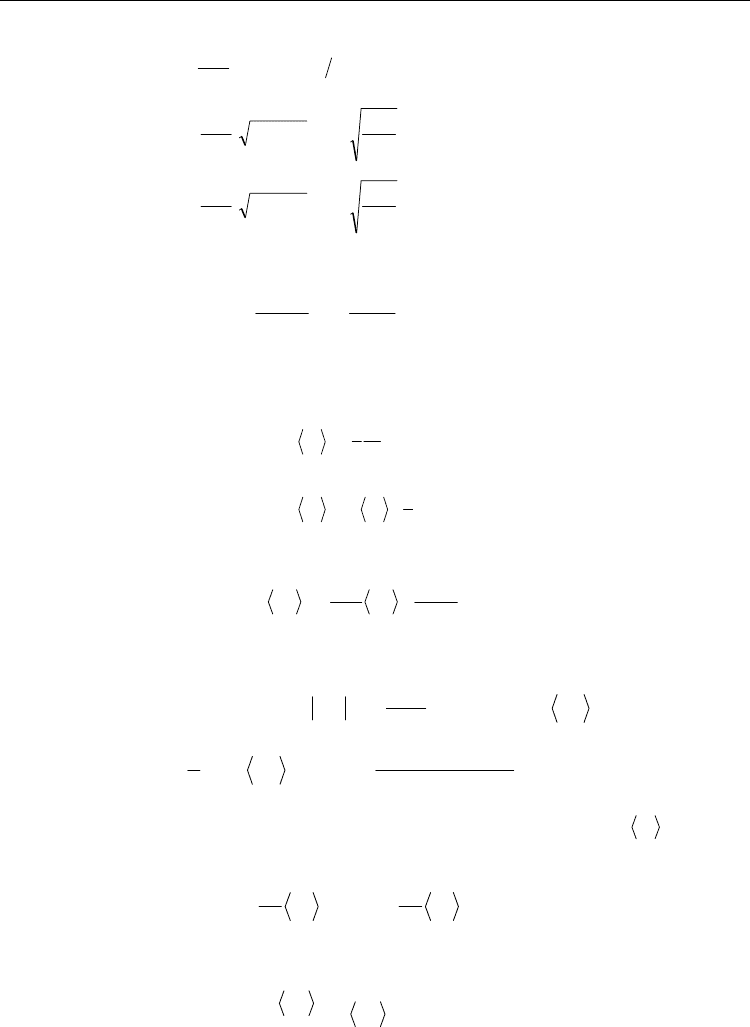
Ferroelectrics - Characterization and Modeling
330
,xx
=
∞
=
∞
=
1
C
0
!
exp
φφ
!
()
()
()
()
()
,pz
A
T
T
yypy
A
T
T
QQTHZ
S
S
S
N
N
S
SSSS
S
N
N
S
SStr
N
tr
∏
∏
∏
≡
−−=
−=
∞
∞−
∞
∞−
4
B
3
B
6
22
4
B
3
B
6
B
6
k
k2
h
1
d2exp
k
k2
h
1
ddkexp
h
1
π
π
(10)
where z(p
S
) satisfies a differential equation (Y. Onodera,1970):
() ()
()
2
2
dd
20
d
d
.
SS
SS
S
S
zp zp
pzp
p
p
−−=
(11)
The solution z(p
S
) is expressed later by the confluent hyper geometric function. The thermal
averages of
2
S
y
and
4
S
y
are easily obtained as
()
2
42
1d
ln
2d
1
4
.
SS
SS
yzp
p
ypy
=−
=− +
(12)
Thus,
42
1
.
24
S
SS
SS
B
QQ
AA
β
=− +
(13)
The free energy given by eq. (9) is rewritten as
()
()
()()
()
.
A
PzT
TQB
Qc
!
q
qqVF
S
S
S
S
SS
nnS
C
S
nn
S
/
S
nnq
−−
+=
′
∞
=
′
−
′
1/42
3/2
3/4
B
1/4
B
2
2
ke
k
2
1
i
iexpd
π
ln
1
1
12
a
(14)
where the potential is decomposed into the Fourier component. The notation
C
denotes
the cumulant as defined by
(15)
It is evident from the formula of the trial Hamiltonian that
0
0
0:
,
:
n
Sn
S
nodd
Q
Q n even
=
thus the cumulant expansions are as follows:
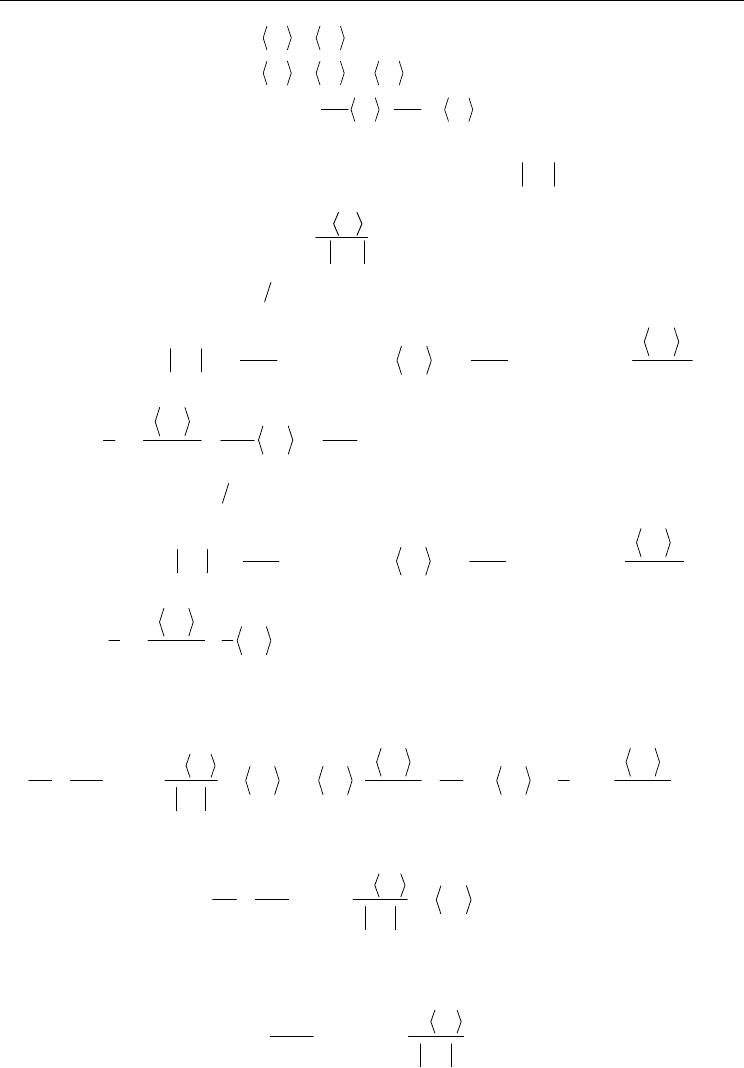
Self-Consistent Anharmonic Theory and Its Application to BaTiO
3
Crystal
331
B
k
22
2
44 2
0
2
22
3
3
24
SS
C
SS S
C
S
SS
SS
QQ
QQ Q
B
T
QQ
AA
=
=−
=− + −
(16)
From the variation of the free energy with the interatomic distance
nn
′
a
, we have the equation
.
V
nn
0=
∂
∂
′
a
(17)
From the optimum condition
0=∂∂
S
AF
gives the relation
()
()
()
()
.
A
T
Q
A
B
A
Q
B
A
Q
c
q
Qc
q
qqV
S
S
S
S
S
S
S
S
S
nn
S
/
nn
S
nn
S
/
S
nnq
0
4
k
22
1
!
i
1
!
i
iexpd
B
0
0
1
C
12
C
12
=+−
∂
∂
−
∂
∂
+
∞
=
′
−
′
∞
=
′
−
′
S
1
1
a
(18)
The optimum condition
0=∂∂
S
BF
gives the relation
()
()
()
()
.Q
B
Q
B
B
Q
c
q
Qc
q
qqV
S
S
S
S
S
S
nn
S
/
Snn
S
nn
S
/
S
nnq
0
2
1
2
1
!
i
!
i
iexpd
0
0
1
C
12
C
12
=+
∂
∂
−
∂
∂
+
∞
=
′
−
′
∞
=
′
−
′
11
1
a
(19)
From eq. (18) and eq. (19), an equation to be satisfied in the thermal equilibrium state is
obtained as
()
.
B
Q
TQB
AA
Q
QQ
V
c
AA
B
S
S
SS
SS
S
SS
nn
nn
S
nn
S
SS
S
0k
2
11
6
2
1
0
2
B
0
2
0
2
0
2
0
2
2
2
2
=
∂
∂
−+
∂
∂
+
∂
∂
−
′
′
′
a
(20)
It is obtained the solution for the anharmonic system as follows:
()
.Q
V
c
AA
B
S
nn
nn
S
nn
S
SS
S
06
2
1
0
2
2
2
2
=+
∂
∂
−
′
′
′
a
(21)
Substituting eq. (21) into eq. (19), an important equation to determine the equilibrium
condition for the free energy is obtained as
()
.
V
c
A
nn
nn
S
S
nn
S
S
01
24
1
1
4
4
4
=
∂
∂
−
′
′
′
a
(22)

Ferroelectrics - Characterization and Modeling
332
()
()
()
()
()
()
[]
,ppppp
p;,pp;,pz
+−+−+−=
−=
5
20
7
4
24
5
32
2
1
4
1
2
1
2
21Γ
δδ
2
3
4
3
4
3
2
2
1
4
1
4
1
2
1
FΓFΓ
()
()
()
,
zz
z;, +
+
+
++=
2!1
1
1!
F
2
γγ
αα
γ
α
γα
1
In high temperature region ( p≪1 ), the solution for eq. (11) is given by
(23)
where
()
()
3380
4
1
4
3
.≅≡
Γ
Γ
δ
and F is the confluent hyper geometric function defined as
(24)
As a result, the average of Q
S
2
is determined as
()
2232
B
1
2
k
14 4
SSS
S
T
Qpp
A
δδδ
=−−++
(25)
In high temperature approximation, the equation for
S
A
to satisfy eqs. (21) and (25) is
obtained as
2
B
2
2C
k
4
,
S
S
f
T
A
f
δ
ν
≅+
(26)
where C =δ
2
-1/2 and
B
k
2
,
S
S
T
B
ν
≡
(27)
()
()
.
V
c
V
c
f
nnS
nn
S
nn
S
nn
nn
S
nn
S
′
′
′
′
′
′
∂
∂
∂
∂
≡
1
4
4
4
2
2
2
a
a
(28)
To substitute eq. (26) into eq.(22), the equation for determining the instability phenomena in
the crystal is obtained as
()
B
2
2
k
2C
6
,
S
f
T
f
f
δ
ν
=
+
(29)
where
() ( )
.
V
cf
nn
nn
S
nn
S
′
′
′
∂
∂
≡
2
2
22
a
(30)
3. Soft mode
The aim of this section is as follows: the author derives equations to determine the soft
mode which minimizes the k-dependent part of the second order term in the trial potential,
Self-Consistent Anharmonic Theory and Its Application to BaTiO
3
Crystal
333
and apply the result to the transition from cubic to tetragonal phase in a ferroelectric crystal
BaTiO
3
. The force constants between atoms are estimated by comparing the theoretical
result for dispersion relations derived from a dynamical matrix with that of a neutron
diffraction experiment (G. Shirane et.al., 1967; B. Jannet et al., 1984). The author applies the
result to determination equations, and verify that the lowest frequency mode at Γ point
corresponds to a mode causing the ferroelectric phase transition of BaTiO
3
.
3.1 Determination equations for the soft mode
It is considered that the crystal instability takes place when the coefficient of the second
order term in the trial potential becomes infinitesimal as temperature approaches to the
transition point. Namely, the parameter ν
S
increases to an unlimited extent. This type of
phase transition accompanied by the symmetry change is suggested as the softening in the
crystals (W. Cochran, 1959). The instability temperature T
C
is defined by the temperature
where
ν
S
→∞ in eq.(29) as
()
BC
2
2
k
6
.
f
T
f
δ
∞
∞
=
(31)
where
∞
f
and
()
2
∞
f
mean the values of
f
and
()
2
f
under
∞→
S
ν
. In the vicinity of the
instability temperature, the parameter
S
ν
can be represented from eqs.(29) and (31) as:
()
()
4
BC
2
2
3
k
C
1
,
S
TT
ff
δ
ν
∞∞
≅−
(32)
where the instability temperature is obtained as
()
()
.
V
c
V
c
T
nn
nn
S
S
nn
S
nn
nn
S
nn
S
S
S
′
∞→
′
′
′
∞→
′
′
∂
∂
∂
∂
=
ν
ν
δ
4
4
4
2
2
2
2
2
B
C
1
6
k
a
a
(33)
Consequently, the variational parameter of the second order term is given as
()
()
()
,TT
V
c
V
c
B
nn
nn
S
nn
S
nn
nn
S
S
nn
S
S
S
S
−
∂
∂
∂
∂
=
′
∞→
′
′
′
∞→
′
′
CB
2
2
2
4
4
4
2
k
1
4C
ν
ν
δ
a
a
(34)
and the variational parameter of the forth order term is also calculated as:
()
.
V
cA
S
nn
S
nnS
nn
SS
∞→
′
′
′
∂
∂
=
ν
4
4
4
1
24
1
a
(35)
Ferroelectrics - Characterization and Modeling
334
()( )
,QAQTTBV
,R,R,RR,R
42
C
kkkk
k
+−=
() () ()
()
.ememc
n
,Rn
,n
,Rn,nn
nn
,R
′
−
′
−
′
′
−=
α
αα
α
kkk
1/21/2
() ()
.,
RR
00grad
2
>∇=
kk γγ
Near the instability temperature, the optimum value of the trial potential is represented as
(36)
where the degree of freedom of the system, S = 3N, is replaced by the branch and the wave
vector (R,
k
). In order that the softening may actually occur, it is necessary that
()
k
R
B
becomes minimum at the definite
k
vector which is written as
()
()
()
()
,
V
c
V
c
B
R
nn
nn
nn
,R
nn
nn
,R
nn
,R
R
k
a
a
k
k
k
k
k
k
γ
δ
ν
ν
∝
∂
∂
∂
∂
=
′
∞→
′
′
′
∞→
′
′
2
2
2
4
4
4
B
2
1
4C
k
(37)
where
()
k
R
γ
is the
k
-dependent part in
()
k
R
B
as
()
()
()
,
c
c
nn
nn
,R
nn,R
nn
,R
R
′
′
′
′
≡
2
4
1
k
k
k
kγ
(38)
(39)
Here, the eigenfunctions
()
α
,n
,R
e
k
of the dynamical matrix given approximately in Appendix
can be easily derived. Consequently, determination equations for the soft mode identified
by (R, k) are given by
(40)
First, whether or not the crystal instability takes place is decided by the temperature
dependence of the second order term in the trial potential as shown in eq. (36). Next, the soft
mode is identified by the determination equations formalized by eq.(40). To apply the
equations, the eigenfunctions included in eq. (39) are necessary which are obtained through
the eigenvalue problem of the dynamical matrix. Landau theory presents that only one
irreducible representation takes part in the phase transition accompanied by the symmetry
change. When more than two modes belong to the same irreducible representation, it is
unknown which mode corresponds to the soft mode with the lowest frequency. In this
section, the author shows that one can solve this difficulty by using eq.(40) as the
determination equations for the soft mode.
3.2 Application to the ferroelectric crystal BaTiO
3
The author constructs a formalism to specify the atomic displacement pattern in softening of
the BaTiO
3
crystal. The Bravais lattice of this crystal above the transition temperature is a
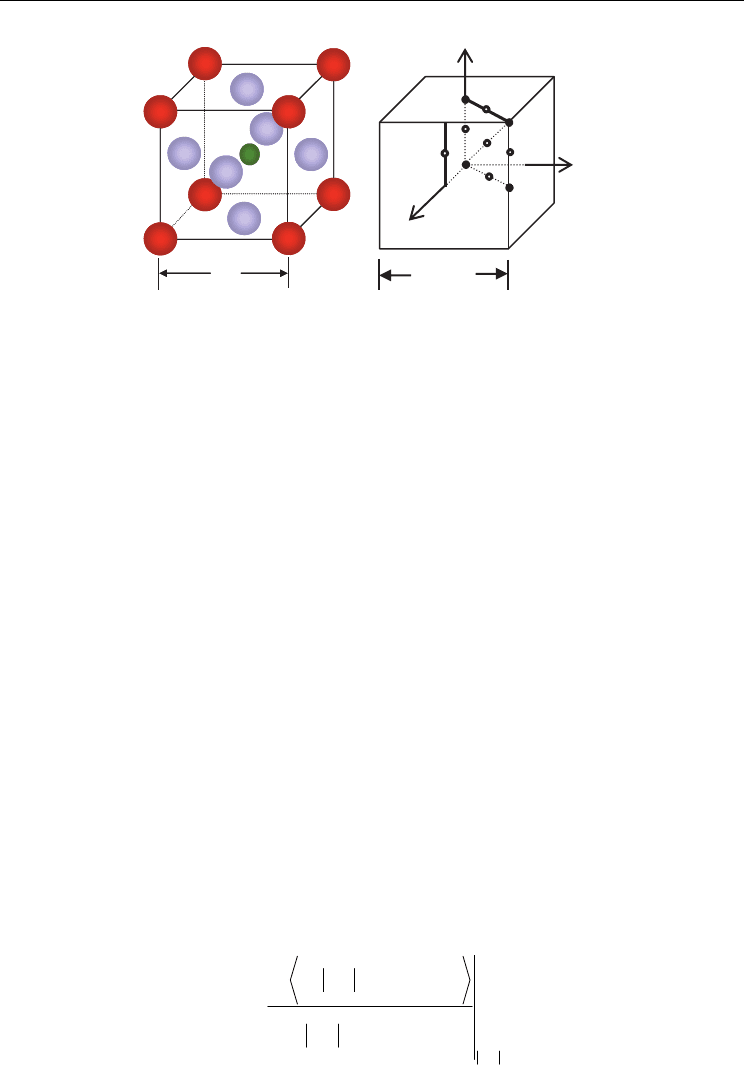
cubic lattice whose unit cell and Brillouin zone are shown in Fig.1.
.
Self-Consistent Anharmonic Theory and Its Application to BaTiO
3
Crystal
335
a
Ti
y
O
Ba
z
O
x
O
a
Ti
y
O
Ba
z
O
x
O
(a) (b)
Fig. 1. Cubic structure and Brillouin zone of BaTiO
3
at high temperature. (a)The atoms in a
unit cell are arranged at the original (n
x
, n
y,
n
z
) for Ti, the corner (n
x
+1/2, n
y
+1/2, n
z
+1/2)
for Ba and the face center (n
x
+1/2, n
y
, n
z
) for O, respectively. The atomic masses are defined
as M
B
, M
T
and M
O
for Ba, Ti and O, respectively. (b) The optical modes discussed in this
work are restricted within the neighborhood of Γ point along the k
Z
axis limits.
When the temperature decreases just below the transition temperature, a freezing of the
mode that Ti and O ions vibrate reversely along the <001> direction of the crystal causes the
structural phase transition from cubic to tetragonal symmetry under softening.
The atomic displacement patterns for vibrational modes at Γ point belonging to the
irreducible representation of space group
1
h
O
are derived by using the method of projection
operator as (G. Burns, 1977)
1u 2u
4T T ,+
(41)
These modes are three-fold degenerate in accordance with the three-dimensional irreducible
representation
T
. There are five branches which consist of one acoustical branch and four
optical branches, named A, O
1
, O
2
, O
3
and O
4.
The Slater(S), Last (L), Bending (B) modes and
so on can be constructed by a combination of atomic displacements which form the basis
functions of
1u
T
. However, one is not able to decide from the group theory which mode
appears actually.
The dispersion relations
2
k
,R
ω
depend upon the force constants, shown in Fig. 2 , which are
derived from the second-order derivative of the interatomic potential with respect to the
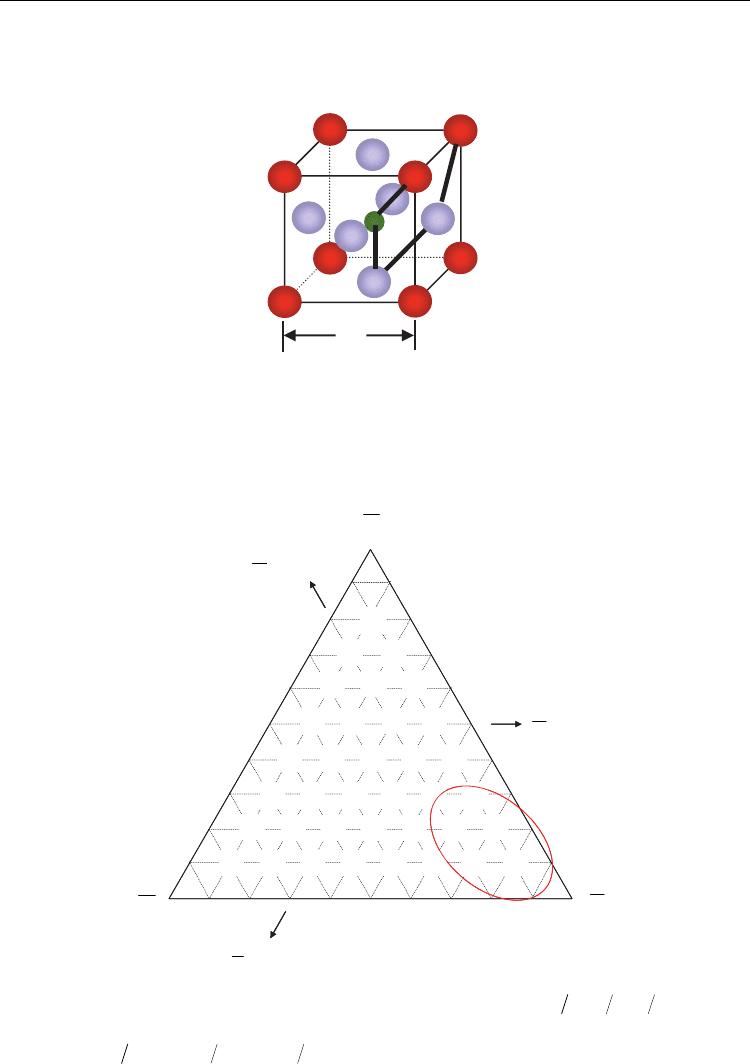
interatomic distance, and defined as
,,,,
TiBaOOOBaOTi −−−−
====
κ
γ
κ
η
κ
β
κ
α
(42)
where
()
()
.
Qc
QcV
nn
S
S
nn
Snn
S
S
nn
Snn
nn
′
+∂
+∂
=
′
′
′
′
′
a
a
a
2
2
κ
T
S
X
R
Δ
Λ
Z
M
Σ
Γ
x
k
y
k
z
k
a/
π
2
Ferroelectrics - Characterization and Modeling
336
It is, however, difficult to estimate the force constants because the various interactions
between atoms exist. The author attempt to decide them so as not to contradict the results
by the neutron diffraction experiment (G.Shirane et al., 1967; B. Jannet et al.,1984).
Fig. 2. Definition of the force constants between atoms: α, β, γ and η for Ti-O, Ba-O, Ti-
Ba and O-O, respectively.
All the six optical modes which are capable of appearing under the various force constants
are obtained by solving the dynamical matrix. In the low frequency region of the dispersion
2
S
L
L
L
1
S
1
S
1
S
1
S
1
S
1
S
1
S
1
S
1
S
1
S
1
S
1
S
B
B
B
BB
B
BB
B
B
γ
α
γ
β
γ
η
B B L
L
∗
L
L
L
L
2.0=
γ
β
5.0=
γ
α
3.0=
γ
η
L
L
2
S
L
L
L
1
S
1
S
1
S
1
S
1
S
1
S
1
S
1
S
1
S
1
S
1
S
1
S
B
B
B
BB
B
BB
B
B
γ
α
γ
β
γ
η
B B L
L
∗
L
L
L
L
2.0=
γ
β
5.0=
γ
α
3.0=
γ
η
L
L
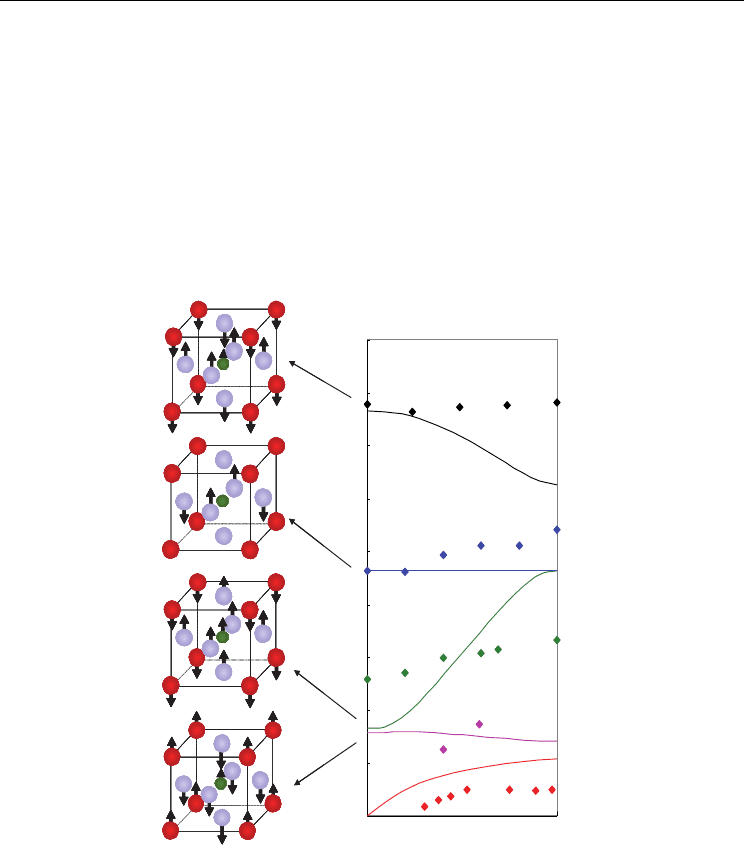
Fig. 3. Triangular diagram composed of the relative force constants
()
γ
η
γ
β
γ
α
,,
. The
notation L* means that the Last mode corresponds to the lowest frequency mode at the
coordinates
()
3.0,2.0,5.0 ===
γ
η
γ
β
γ
α
.
η
α
β
γ
a
Self-Consistent Anharmonic Theory and Its Application to BaTiO
3
Crystal
337
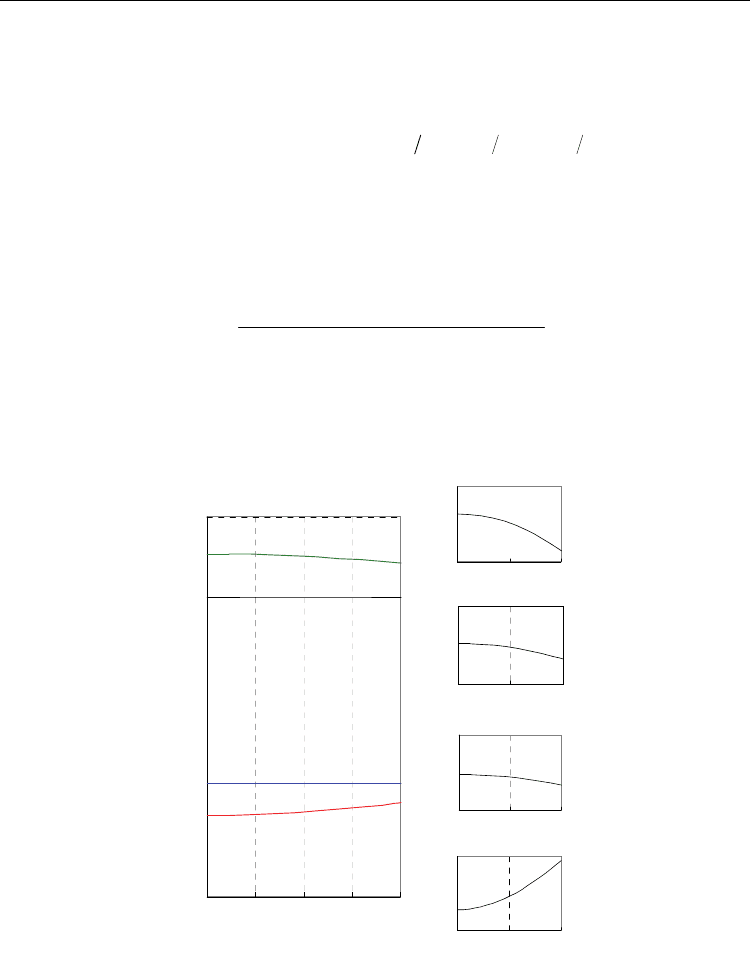
curves, only two modes always appear within the set of four modes L, B, S
1
and S
2
. The
other two modes T
2u
and Plane appear constantly in the high frequency region. It is well-
known that the Slater mode is considered to be an optical lattice vibration in which Ti-
sublattice vibrates in the reverse direction to O-octahedron. Until now, it has been sufficient
to treat the displacements for only Ti and O ions, to explain qualitatively the appearance of
an electric polarization. Though the motion of Ba-sublattice has been neglected in the past,
the displacements for Ba ions must be considered in the case that the dispersion relations are
compared between the theory proposed here and the experiment by the neutron diffraction.
There are two kinds of the Slater mode: S
1
in which Ti-sublattice vibrates in the reverse
direction to Ba-sublattice and O-octahedrons, and S
2
in which Ba-sublattice and Ti-sublattice
vibrate in the reverse direction to O-octahedrons.
arb. unit
()
kω
Δ
4
O
3
O
2
O
1
O
A
Χ
Γ
arb. unit
()
kω
Δ
4
O
3
O
2
O
1
O
A
Χ
Γ
(a) (b)
Fig. 4. Dispersion curves with the force constants (α/γ=0.1, β/γ=0.09, η/γ=0.81)
of BaTiO
3
. (a) The lowest frequency mode at Γ point for each branch is shown with the
atomic displacement patten. (b) The solid curves represent the theoretical values for
the dispersion relations derived from eq. A-1. Small rectangles correspond to the
experimental results. (Y.Aikawa & K.Fujii, 2011 to be published in Ferrolelectrics)
The triangular coordinates are introduced whose three axes mean the ratio of α, β and η
normalized by γ, namely, α/γ, β/γ, η/γ. The triangular diagram in Fig.3 shows
Plane
u2
T
L
2
S
Ferroelectrics - Characterization and Modeling
338
()
() ( ) () ( )
(
)
() ( ) () ( )
,
cccc
cccc
,R,R,R,R
,R,R,R,R
R
2BaTi2OO2OBa2OTi
4BaTi4OO4OBa4OTi
1
−−−−
−−−−
+++
+++
=
kkkk
k
kkkk
k
γ
which mode corresponds to the lowest frequency mode for the given coordinates at Γpoint
in the Brilloin zone. The dispersion relations within the region enclosed with an ellipse are
in agreement with the results obtained by the neutron diffraction experiment. The lowest
frequency mode is S
2
mode at the coordinates (α/γ=0.1, β/γ=0.09, η/γ=0.81) in the
enclosed region.
The dispersion curves with the force constants
()
0.1, 0.09, 0.81
αγ βγ ηγ
== = of BaTiO
3
and the experimental values obtained by the neutron diffraction are shown in Fig. 4.
Conversely, the author can estimate the relative force constants of the BaTiO
3
crystal by the
above coordinates.
The (
R, k)-dependent part,
()
k
R
γ
, for the coefficient
()( )
TTB
CR
−
k
of the second order term
in the trial potential is given by
(43)
It is to be noted that the functions
()
nn
,R
c
′
k
are given by the eigenfunctions of the dynamical
matrix which is dependent on the force constants. The author has found that the O
1
branch
corresponding to the S
2
mode at Γpoint tends to decrease in approaching to Γ point and
satisfies with the condition given by eq.(40) as shown in Fig. 5.
0 0.01 0.02 0.03 0.04
×π/a
arb. unit
1
O
2
O
3
O
4
O
()
k
R
γ
L
Plane
u2
T
2
S
0 0.01 0.02 0.03 0.04
×π/a
arb. unit
1
O
2
O
3
O
4
O
()
k
R
γ
L
Plane
u2
T
2
S
0 0.02 0.04
×π/a
arb. unit
00.020.04
×π/a
arb. unit
0 0.02 0.04
×π/a
arb. unit
00.020.04
×π/a
arb. unit
1
O
3
O
4
O
2
O
0 0.02 0.04
×π/a
arb. unit
00.020.04
×π/a
arb. unit
0 0.02 0.04
×π/a
arb. unit
00.020.04
×π/a
arb. unit
1
O
3
O
4
O
2
O
(a) (b)
Fig. 5. The function
()
R
γ
k for the optical branches near Γ point. (a) The k-dependence of
γ
R
(k) for the optical branches derived from eq. (43) shows the softening of O
1
branch at
Γpoint. (b) The details obtained by magnifying the figure (a).
