Лабораторные работы по курсу общей физики (2-я Редакция 2012 г.)

Подождите немного. Документ загружается.

1 Цель работы

Определение коэффициента Пуассона воздуха по данным измерения его давления

после адиабатического расширения и последующего изохорного нагревания.

2 Теория метода

Теплоемкостью тела называют количество теплоты, необходимое для повышения

температуры тела на 1 К. Если телу сообщили количество теплоты d



Q и при этом его

температура изменилась на dT, то теплоемкость тела определяется отношением





(2.1)

Для характеристики тепловых свойств веществ используют понятия удельной (с) и

молярной (С) теплоемкости, определяемых как



















, (2.2)

где m  масса тела;

  число молей вещества.

Теплоемкости C

, c и C зависят от природы вещества и от условий в которых

происходит нагревание. Это следует из первого начала термодинамики

AddUQd







(2.3)

Поскольку

PdVAd 



, (2.4)

где dV – изменение объема тела;

P – давление.

то из (2.2) и (2.3) следует, что молярная теплоемкость физически однородного вещества

определяется соотношением

dVP

C 



























(2.5)

Отношение



(2.6)

теплоемкостей газа при постоянном давлении и постоянном газе называется

коэффициентом Пуассона (иногда – показателем адиабаты). Для идеального газа средняя

энергия теплового движения молекулы газа равна



, (2.7)

где i – сумма числа поступательных, вращательных и удвоенного числа

колебательных степеней свободы молекулы.

Внутренняя энергия  молей газа равна

U 

, (2.8)

где R – универсальная газовая постоянная.

В соответствии с (2.5) и (2.8) молярная теплоемкость идеального газа при постоянном

объеме равна







. (2.9)

Дифференцируя уравнение состояния идеального газа при постоянном давлении,

имеем:

RPdV 

. (2.10)

Из (2.5), (2.9) и (2.10) следует, что молярная теплоемкость идеального газа при

постоянном давлении равна

RCC

2



. (2.11)

Следовательно, коэффициент Пуассона определяется по формуле

i 2



(2.12)

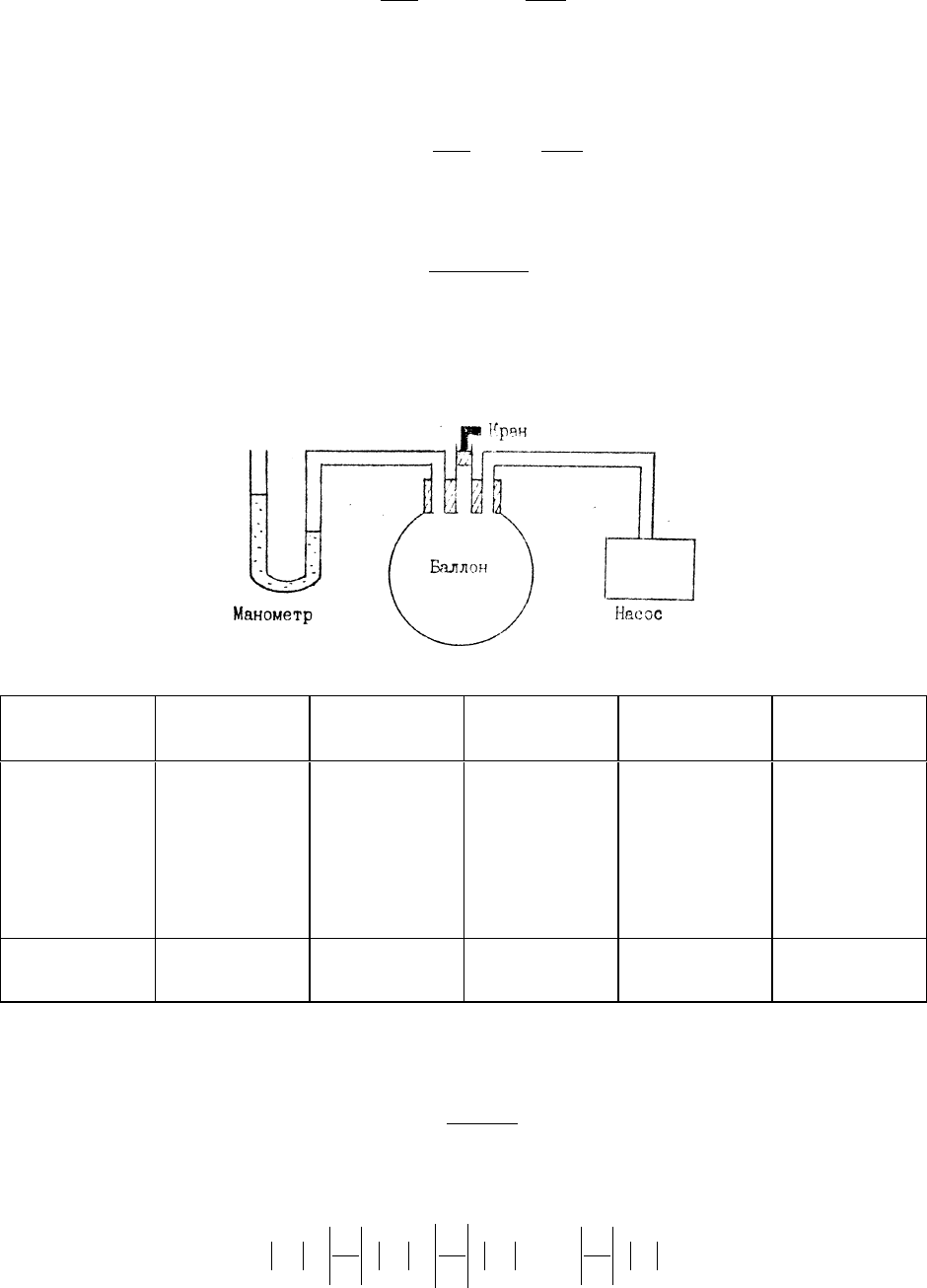
Рассмотрим воздух, содержащийся в каком-то сосуде, сообщающемся с атмосферой.

Если закачать в сосуд некоторое количество воздуха, то давление в сосуде повысится. При

быстром нагнетании воздуха теплообмен между содержимым сосуда и его окружением

произойти практически не успеет и сжатие будет происходить адиабатически и

сопровождаться повышением температуры и давления.

PPP



, (2.13)

где P

– приращение давления, произошедшее фактически за счет увеличения

массы воздуха в сосуде по сравнению с массой в изначальном состоянии.

При быстром открывании крана воздух из сосуда будет расширяться достаточно

быстро и система не успевает обменяться теплом с окружающей средой; происходит

адиабатическое расширение. Этот адиабатический переход воздуха описывается законом

Пуассона:









TPTP

(2.14)

Если после этого снова закрыть кран, то оставшийся воздух начнет изохорно

нагреваться. Когда температуры сосуда и окружающей среды уравновесятся, то давление

в сосуде увеличится на P

и станет равным

PPP



(2.15)

Этот изохорный переход описывается законом Гей-Люссака:



(2.16)

Принимая во внимание (2.13), (2.15) из (2.14) и (2.16) получаем:



































. (2.17)

В случае относительно малых изменений давлений P

и P

по сравнению с

атмосферным давлением P

обе части можно разложить по биному Ньютона:

 

111









, (2.18)

откуда







. (2.19)

3 Экспериментальная часть

3.1 Схема установки

3.2 Результаты измерений

№









0,190

0,036

1,234

0,010

0,772

0,174

0,034

1,243

0,011

0,854

0,136

0,029

1,271

0,014

1,134

0,161

0,031

1,238

0,011

0,917

0,160

0,031

1,240

0,011

0,925

Среднее

значение

0,164

0,032

1,245

0,011

0,921

3.3 Расчет погрешностей





(2.20)

Используя формулу

u  ...

(2.21)

вычисляю абсолютную погрешность :

   











, (2.22)

где h

= 0,001 м.

h

= 0,001 м.

Относительная погрешность рассчитывается по формуле:

%100





(2.23)

Вывод: В результате эксперимента был обнаружен коэффициент Пуассона воздуха по

данным его давления после адиабатического расширения и изохорного нагревания.

Среднее значение коэффициента Пуассона равно  = 1,245  0,011.

Лабораторная работа №17

Опытная проверка уравнения состояния и законов идеального газа.

Цель работы:

1. Изучение физических свойств газов и взаимосвязи параметров, описывающих их состояние, на основе

модели идеального газа

2. Проверка уравнения состояния идеального газа.

3. Определение предельного давления откачиваемого воздуха в вакуумной установке и объема рабочей

камеры насоса.

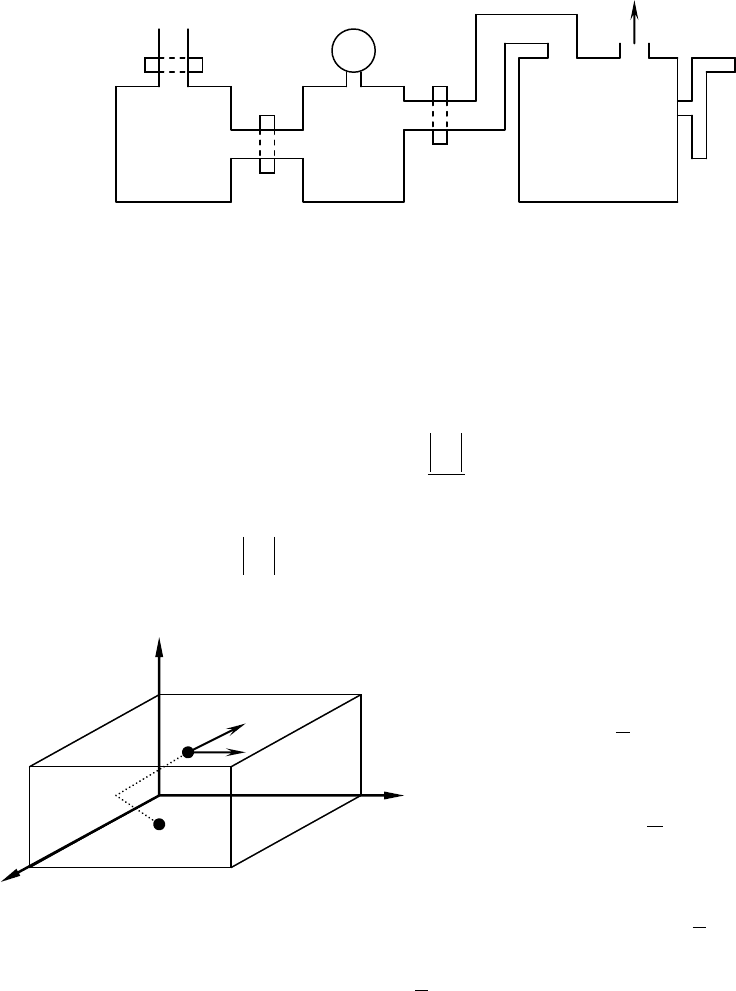
Приборы и принадлежности: два герметичных сосуда (1 и 2), манометр (3), механический насос (4),

краны (5, 6, 7).

Схема установки:

Теория: Под идеальным газом понимается совокупность непрерывно и беспорядочно движущихся

точечных частиц конечной массы, столкновения между которыми происходят по закону абсолютно упругого

удара, причем других способов взаимодействия между частицами нет, то есть силы взаимодействия на

конечном расстоянии отсутствует. Давление, оказываемое идеальным газом на стенки сосуда, в котором

он находится, определяется силами, возникающими при абсолютно упругих соударениях молекул со

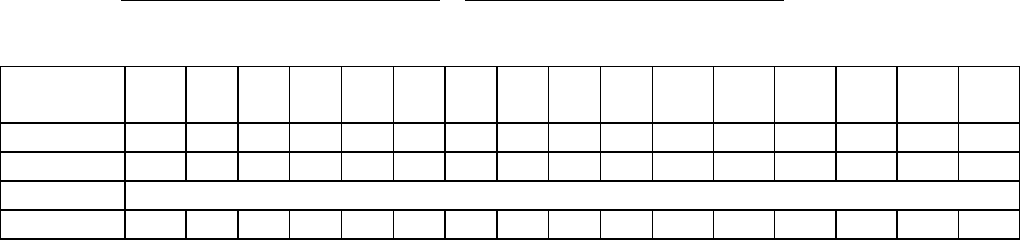
стенками. Рассмотрим одну из молекул, отражающихся от стенки сосуда (рис. 1). Величина средней силы



равна:







(1)

А величина изменения импульса:

 

y0y0y0y

m2mmkk 



(2)

где: m

– масса молекулы

– проекция скорости





на ось Y,

перпендикулярную стенке.

Но средняя сила



равна:

y00y0

SmntSn

oFF 



(3)

Давление Р равно:

y00

P 



(4)

Но





значит:





(5)

Отсюда имеем:

P 



(6)

сомножитель





есть средняя кинетическая энергия теплового движения одной молекулы, имеем:







(7)

Уравнение (7) называется основным уравнением молекулярно кинетической теории газов. Значит:





(8)

где: K = 1,38∙10

-23

Дж

- постоянная Больцмана.

Из уравнения (7) и (8)и получаем состояние идеального газа в виде:

kTnP



(9)

Общее число молекул в сосуде равно N = n

Y. Тогда:

NkTPV 

(10) где

NN 

отсюда:





(11)

где: R = 8.31

Кмоль

Дж



- Универсальная газовая постоянная.

ν 

Уравнение состояния идеального газа, представленного в виде (11) называется уравнением

Менделеева – Клайперона. Т.к. R, m, μ не изменяются для взятого газа, то имеем:

const



(14)

Из уравнения (14):

1. T = const изотерма PV = const (Закон Бойля - Мариотта)

2. P = const изобара V/T = const (Закон Гей - Люссака)

3. V = const изохора P/T = const (Закон Шарля)

Ра, кПа

, кПа

A = P

+ PaV

В = Р

+ V

)

179

0,002

180

0,002

179

0,002

183

0,002

179

0,002

183

0,002

 

2a11

VPVPlnAln 

    

2a11

VPVPlndAlnd 

 

2a11

VPVP

VPVPd





 

2a11

VPVP

VPd

VPVP

VPd





 

2a11

VPVP













 

VPVP

2a11

























 

212

VVPB 

 

VVP

212

























179м10Па1099м102Па1040А

333333





Дж



































333333

м10Па1099м102Па1040

м10Па1

м10Па1099м102Па1040

м10Па1

Дж102Дж179

3



 

180м101м102Па1060В

33333





Дж

   

002,0Дж180

м101м102Па1060

м10Па1

м101м102Па1060

м10Па1

33333



































Дж

Число

тактов

100

110

120

130

140

150

Pi, кПа

100

ln Pi

(14 ± 0,5) кПа

Лабораторная работа №19

по курсу общей физики.

Определение коэффициента Пуассона воздуха акустическим методом.

Выполнил: Усманов К.Р. ИИТ-125

1 Цель работы

Определение коэффициента Пуассона воздуха по данным измерения скорости

распространения в нем звука методом стоячих волн.

2 Теоретическая часть

Теплоемкостью тела называют количество теплоты, необходимое для повышения

температуры тела на 1 К. Если телу сообщили количество теплоты d



Q и при этом его

температура изменилась на dT, то теплоемкость тела определяется как





. (2.1)

Для характеристики тепловых свойств веществ используют понятия удельной (с) и

молярной (С) теплоемкости, определяемых как



















, (2.2)

где m  масса тела;

  число молей вещества.

Теплоемкости C

, c и C зависят от природы вещества и от условий в которых

происходит нагревание. Это следует из первого начала термодинамики

AddUQd







(2.3)

Поскольку

PdVAd 



, (2.4)

где dV – изменение объема тела;

P – давление.

то из (2.2) и (2.3) следует, что молярная теплоемкость физически однородного вещества

определяется соотношением

dVP

C 



























(2.5)

Внутренняя энергия идеального газа – энергия теплового движения молекул и атомов

в молекулах и представляет собой сумму кинетической энергии поступательного и

вращательного движения молекул и энергии колебания атомов. Средняя энергия

молекулы идеального газа равна



, (2.6)

где i – сумма числа поступательных, вращательных и удвоенного числа

колебательных степеней свободы молекулы.

Внутренняя энергия  молей газа равна



, (2.7)

где N

– число Авогадро;

R – универсальная газовая постоянная.

В соответствии с (2.5) и (2.7) молярная теплоемкость идеального газа при постоянном

объеме равна







. (2.8)

Из уравнения состояния идеального газа имеем





. (2.9)

При постоянном давлении

dV 



. (2.10)

Из (2.5) с учетом (2.8) и (2.10) следует, что молярная теплоемкость идеального газа

при постоянном давлении равна

RCC

2



. (2.11)

Отношение теплоемкостей газа при постоянном давлении и объеме

2



(2.12)

называется коэффициентом Пуассона. Это отношение определяется только числом

степеней свободы молекулы газа.

Продольные волны в сплошной среде распространяются со скоростью





, (2.13)

где



 коэффициент сжимаемости среды;

  плотность среды.

При распространении звуковых волн в газе любая небольшая его часть периодически

сжимается и разжимается. В местах сжатия газ нагревается, а в местах разрежения –

охлаждается. В следствии малой теплопроводности газа и большой частоты колебаний

можно считать газ теплоизолированным. В таком случае распространение звука в газе

сопровождается адиабатическим сжатием и разрежением газа.

constPV 



(2.14)

Дифференцируя по P





PVV

, (2.15)

находим производную объема по давлению:





, (2.16)