Лабоцкий В.В. Управление знаниями

Подождите немного. Документ загружается.

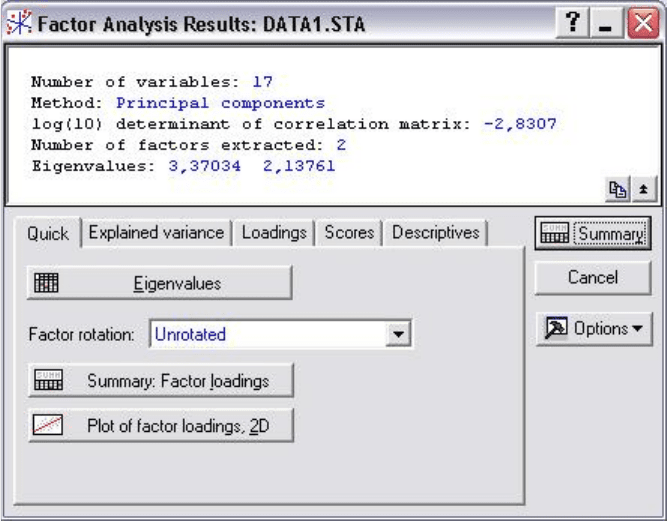
Рис. 7.6

В верхней части окна Результаты факторного анализа дается

информационное сообщение:

Number of variables (число анализируемых переменных) – 17;

Method (метод анализа – главные компоненты);

log(10) determination of correlation matrix (десятичный логарифм

детерминанта корреляционной матрицы) – 2,8307;

Number of Factor extraction (число выделенных факторов) – 2;

Eigenvalues (собственные значения) – 3,37034; 2,13761.

В нижней части окна находятся функциональные кнопки,

позволяющие всесторонне просмотреть результаты анализа численно и

графически.

•

Щелкните на кнопку Plot of factor loadings, 2D (Двумерный

график нагрузок

) и посмотрите результаты факторного анализа на

графике (Рис. 7.7).

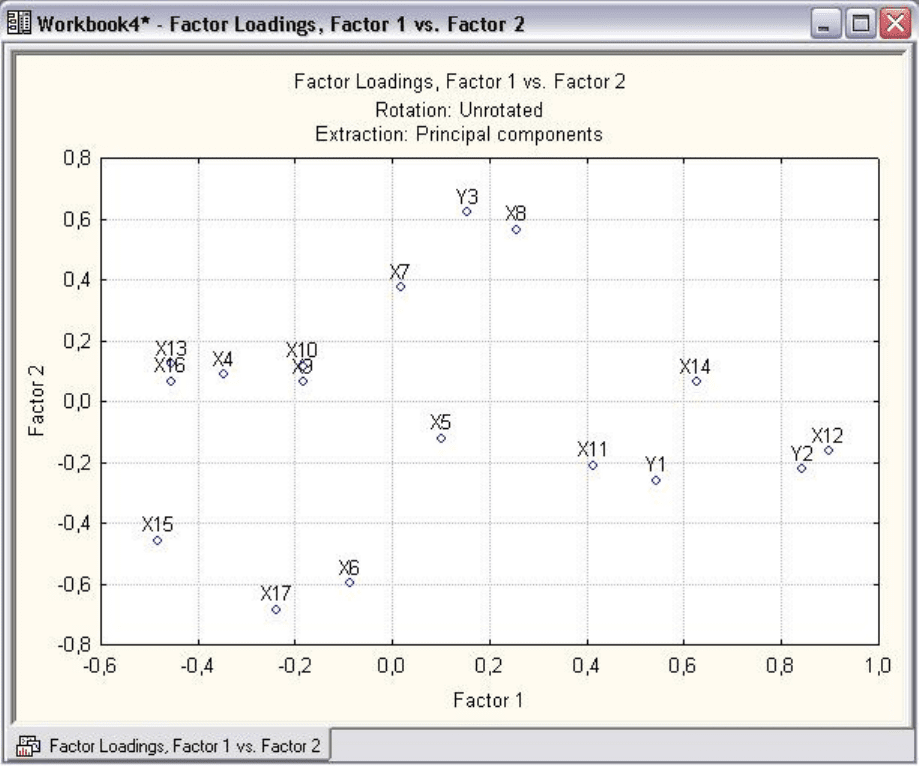
Рис. 7.7

•

Вернитесь в окно Factor Analysis Results и щелкните на кнопке

Summary: Factor Loadings (Факторные нагрузки), и посмотрите

нагрузки численно (Рис. 7.8).

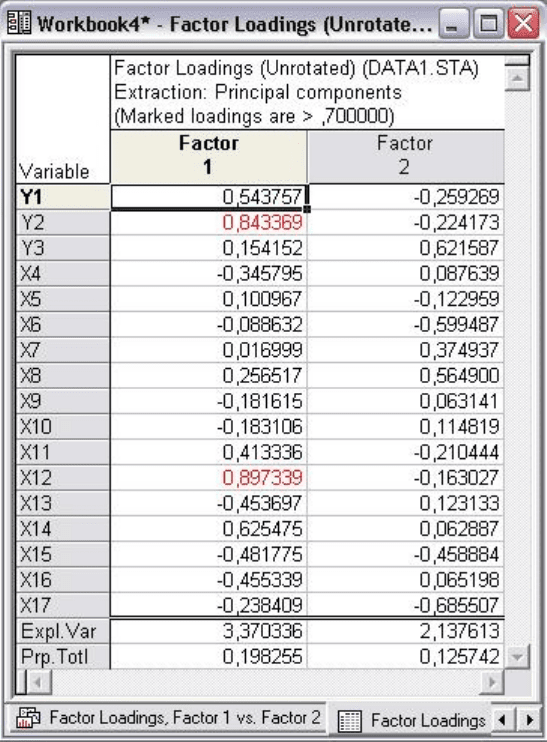
Рис. 7.8

Рассматривая решение на графике, обратите внимание на нагрузки

параметров выделенные красным цветом. Их трудно проинтерпретировать,

возникает вопрос, какой смысл придать второму фактору. В этом случае

целесообразно прибегнуть к повороту осей, надеясь получить решение,

которое можно интерпретировать в предметной области.

•

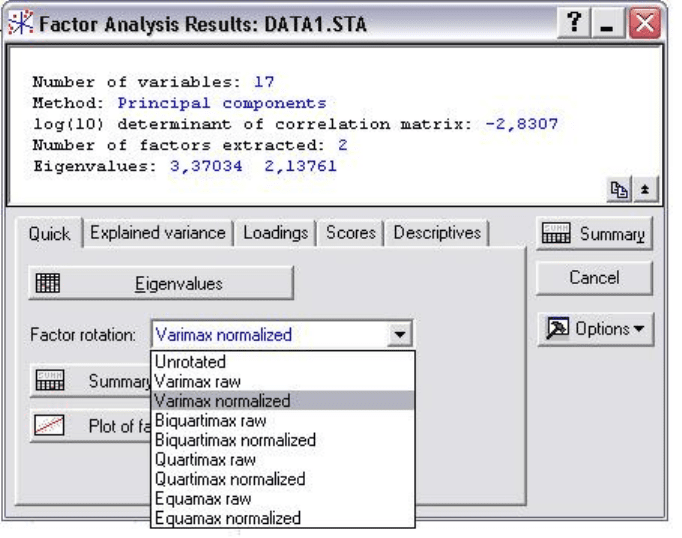
В панели Factor Analysis Results в поле Factor rotation

(Вращение факторов) (Рис. 7.9) вы можете выбрать различные повороты

оси. Окно предлагает несколько возможностей оценить и найти нужный

поворот следующими методами:

Varimax – Варимакс;

Biquartimax – Биквартимакс;

Quartimax – Квартимакс;

Equamax – Эквимакс.

Цель вращения – получение простой структуры, при которой

большинство наблюдений находится вблизи осей координат. При

случайной конфигурации наблюдений невозможно получить простую

структуру.

Рис. 7.9

Дополнительный термин в названии методов –

normalized

(нормализованные) – указывает на то, что факторные нагрузки в процедуре

нормализуются, т.е. делятся на корень квадратный из соответствующей

дисперсии. Термин

raw (исходные) показывает, что вращаемые нагрузки

не нормализованы.

Инициируйте

Varimax normalized (Варимакс нормализованный).

Система произведет вращение факторов методом нормализованного

варимакса, и окно

Factor Analysis Results (Результаты факторного

анализа

) снова появится на мониторе. Вновь инициируйте в этом окне

кнопку

Plot of factor loadings, 2D (Двумерный график нагрузок)

(Двумерный график нагрузок). Вы опять увидите график нагрузок (Рис.

7.10).

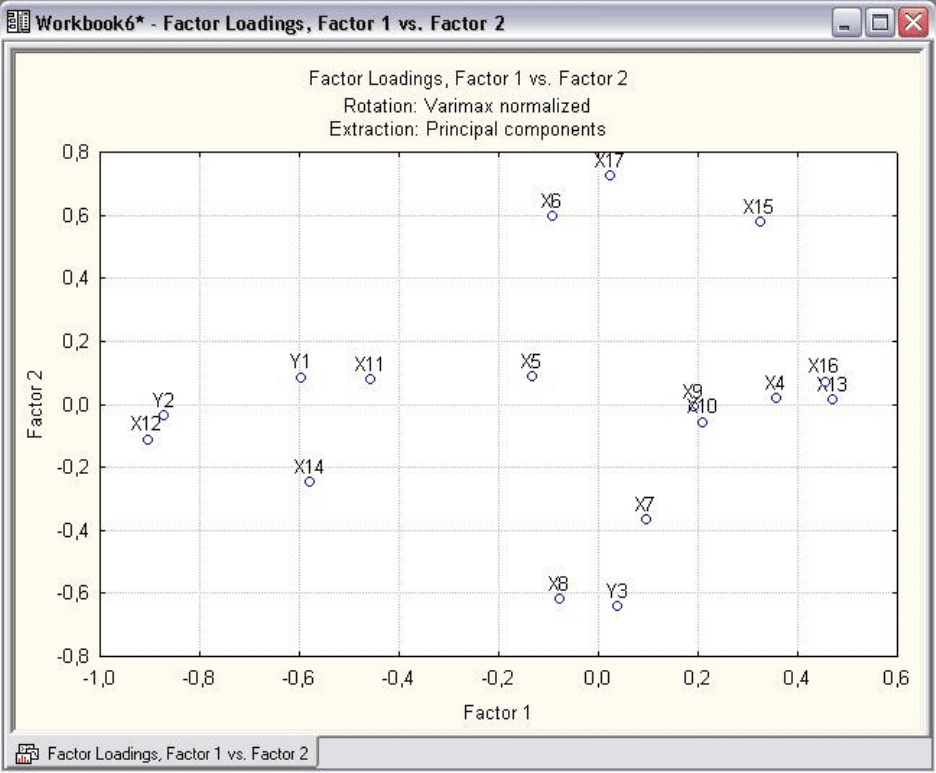
Рис. 7.10

Конечно, этот график немного отличается от предыдущего.

Посмотрим еще нагрузки численно, инициировав кнопку

Summary: Factor

loadings (Факторные нагрузки) в окне Factor Analysis Results (Рис. 7.11).

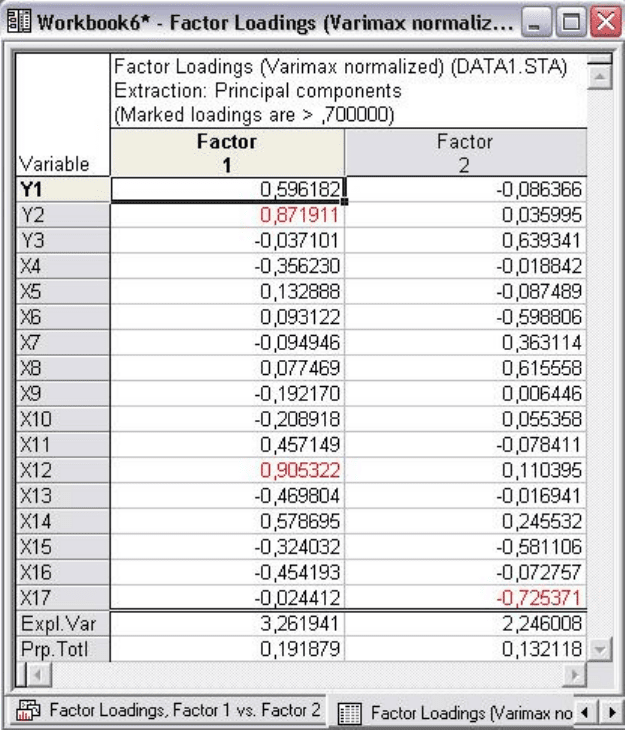
Рис. 7.11

Теперь найденное решение уже можно интерпретировать. Факторы

чаще интерпретируют по нагрузкам. Первый фактор теснее всего связан с

Y2 – индексом снижения себестоимости продукции и X12 – среднегодовой

стоимостью ОПФ. Общая стоимость содержания ОПФ состоит из

первичных инвестиционных затрат и дальнейших эксплуатационных

расходов, зависящих от объема производства. Второй фактор (только с

одним

показателем) X17 – непроизводственные расходы.

Возникает вопрос: сколькими же факторами следует ограничиваться

на практике? Для этого в программном пакете

STATISTICA существует

критерий

Scree plot (Критерий каменистой осыпи) в закладке Explained

variance (Рис. 7.12) окна

Factor Analysis Results.

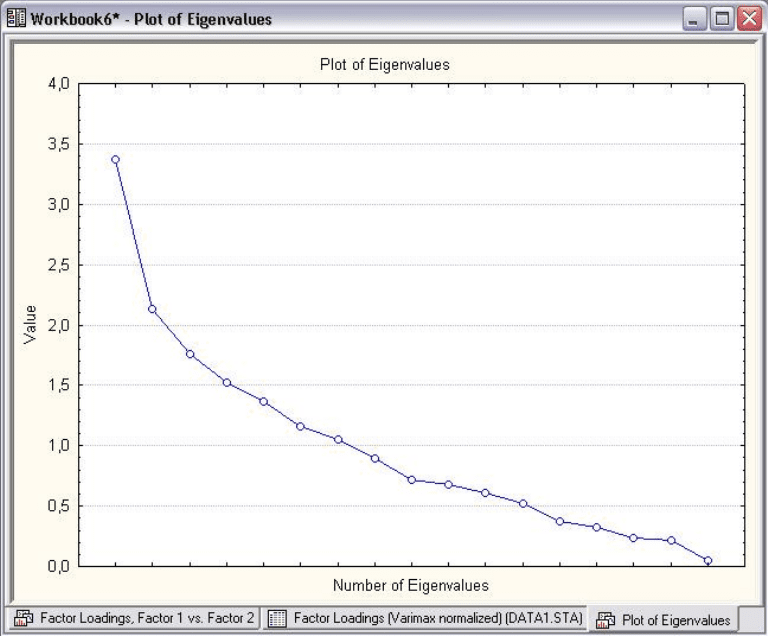
Рис. 7.12

В точках с координатами 1, 2 осыпание замедляется наиболее

существенно, следовательно, можно ограничиваться одним или двумя

факторами.

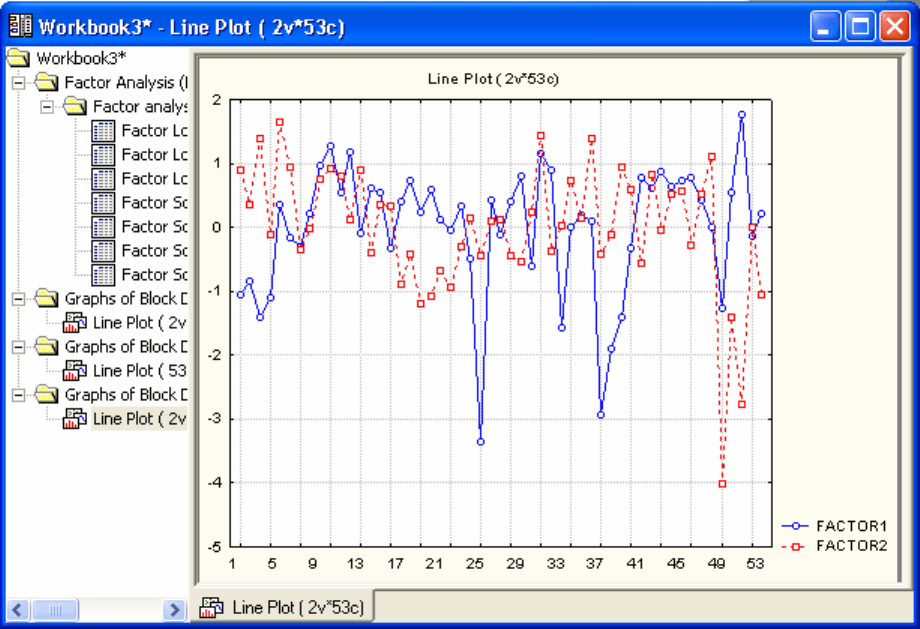
Система

STATISTICA позволяет определить нормированные

значения этих факторов (кнопка

Factor scores) и построить графики,

предварительно выделив эти столбцы, вызвать контекстное меню правой

клавишей мыши и дать команду

Graphs of BlockData/Line Plot: Entire

Columns

. Интерпретация этих графиков (Рис. 7.13) остается за

специалистом в данной предметной области.

Рис. 7.13

8. "ДЕРЕВЬЯ РЕШЕНИЙ"

 Против каждой стрелки значилось: направо -

"Получишь то, что захочешь, но не

удержишь"; налево - "Удержишь то, что

получишь, но не захочешь"; прямо - "Захочешь

то, что удержишь, но не получишь"

Е. Клюев "Между двух стульев"

8.1. ОБЩИЕ СВЕДЕНИЯ

"Деревья решений" (классификации) – это метод, позволяющий

предсказывать принадлежность наблюдений или объектов к тому или

иному классу категориальной зависимой переменной в соответствии со

значениями одной или нескольких предикторных переменных.

Иерархическое строение "дерева классификации" – одно из наиболее

важных его свойств. "Стволом дерева" является проблема или ситуация,

требующая решения. "Вершиной дерева" являются

цели или ценности,

которыми руководствуется человек, принимающий решение.

Первые идеи создания деревьев решений восходят к работам

Ховленда (Hoveland) и Ханта (Hunt) конца 50-х годов XX века. Однако,

основополагающей работой, давшей импульс развитию этого направления,

явилась книга Ханта (Hunt, E.B.), Мэрина (Marin J.) и Стоуна (Stone P.J)

"Experiments in Induction", увидевшая свет в 1966 г.

8.2. ТЕРМИНОЛОГИЯ

Введем основные понятия из теории "деревьев решений" (табл. 8.1).

Таблица 8.1

Название Описание

Объект Пример, шаблон, наблюдение

Атрибут Признак, независимая переменная, свойство

Метка класса Зависимая переменная, целевая переменная, признак,

определяющий класс объекта

Узел Внутренний узел дерева, узел проверки

Лист Конечный узел дерева, узел решения

Проверка Условие в узле

8.3. ЧТО ТАКОЕ "ДЕРЕВО РЕШЕНИЙ" И ТИПЫ РЕШАЕМЫХ

ЗАДАЧ?

"Деревья решений" – это способ представления правил в

иерархической, последовательной структуре, где каждому объекту

соответствует единственный узел, дающий решение.

100

Под правилом понимается логическая конструкция, представленная в

виде "если … то …".

Область применения деревья решений в настоящее время широка, но

все задачи, решаемые этим аппаратом могут быть объединены в

следующие три класса:

•

описание данных: "деревья решений" позволяют хранить

информацию о данных в компактной форме, вместо них мы можем

хранить дерево решений, которое содержит точное описание объектов;

•

классификация: "деревья решений" отлично справляются с

задачами классификации, т.е. отнесения объектов к одному из заранее

известных классов. Целевая переменная должна иметь дискретные

значения;

•

регрессия: если целевая переменная имеет непрерывные значения,

"деревья решений" позволяют установить зависимость целевой

переменной от независимых (входных) переменных. Например, к этому

классу относятся задачи численного прогнозирования (предсказания

значений целевой переменной).

8.4. КАК ПОСТРОИТЬ "ДЕРЕВО РЕШЕНИЙ" ?

На сегодняшний день существует значительное число алгоритмов,

реализующих деревья решений CART, C4.5, NewId, ITrule, CHAID, CN2 и

др. Но наибольшее распространение и популярность получили следующие

два:

•

CART (Classification and Regression Tree) – это алгоритм

построения бинарного "дерева решений" – дихотомической

классификационной модели. Каждый узел дерева при разбиении имеет

только двух потомков. Как видно из названия алгоритма, он решает задачи

классификации и регрессии;

•

C4.5 – это алгоритм построения "дерева решений", количество

потомков у узла не ограничено. Не умеет работать с непрерывным

целевым полем, поэтому решает только задачи классификации.

В пакете Statistic в модуле "Деревья классификации" реализованы три

метода:

•

дискриминантное одномерное ветвление по категориальным и

порядковым предикторам;

•

дискриминантное многомерное ветвление по линейным

комбинациям порядковых предикторов;

•

одномерное ветвление по методу CART.

Первые два представляют собой адаптацию соответствующих

алгоритмов пакета

QUEST (Quick, Unbiased, Efficient Statistical Trees).