Лабоцкий В.В. Управление знаниями
Подождите немного. Документ загружается.

51
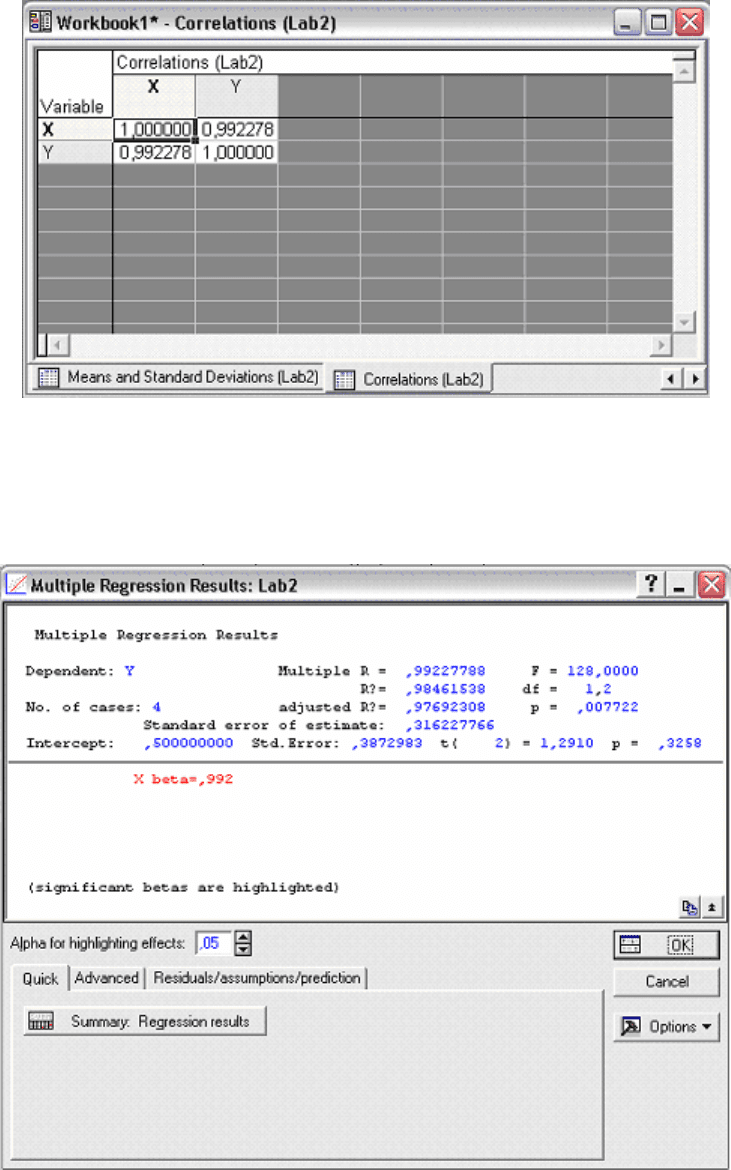
Рис. 3.16
•
затем снова в окне Descriptive Statistics нажмите ОК. Появится
окно (Рис. 3.17).
Рис. 3.17
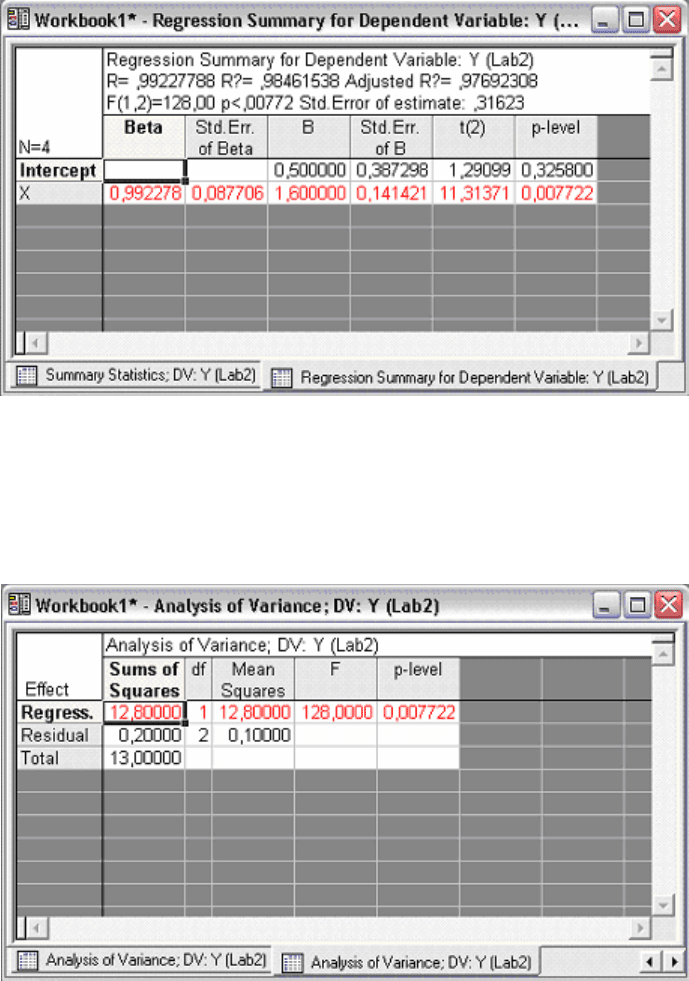
• выберите закладку Advanced и нажмите кнопку Summary:
Regression results
для расчета параметров модели и коэффициентов
Стьюдента (Рис. 3.18)
.
52
Рис. 3.18
•
Затем кнопку ANOVA (Overall goodness of fit) для расчета
таблицы адекватности и соответствующих QR , QE , Q, k, n–k–1, F, S (Рис.
3.19).
Рис. 3.19
•
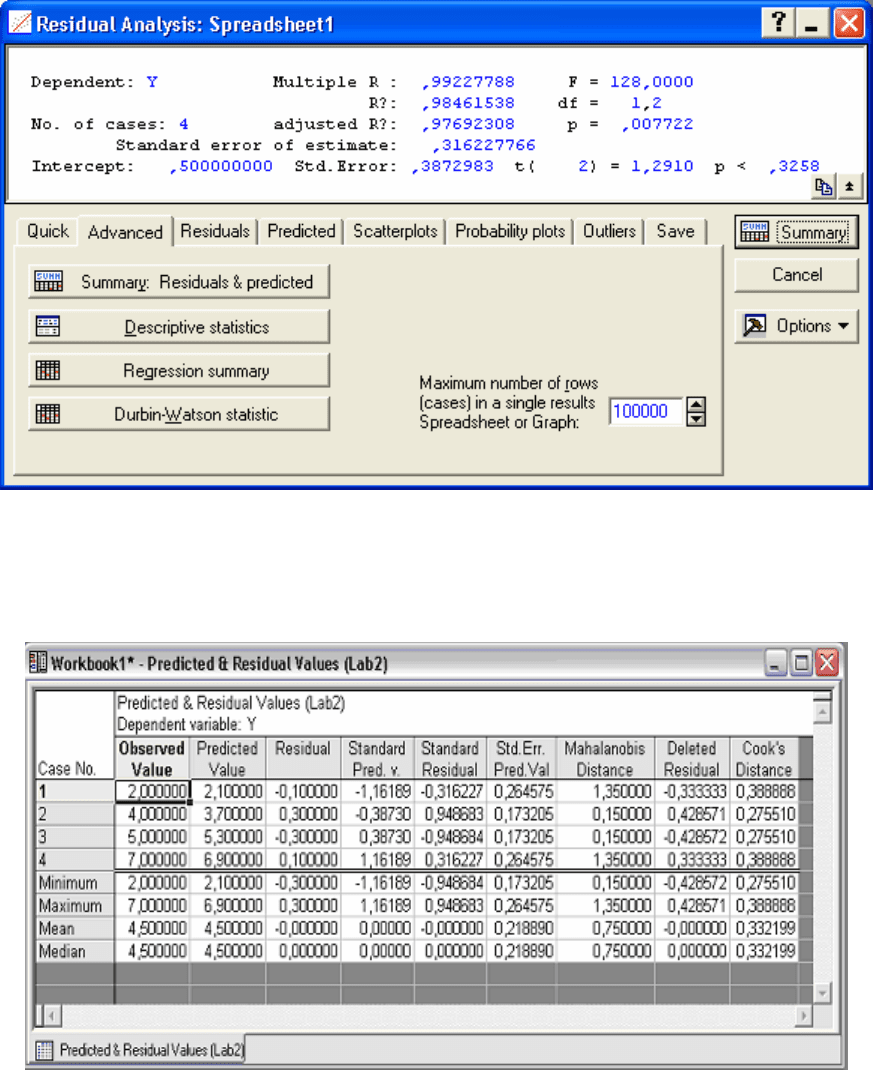
В окне Multiple Regression Results нажмите OK. Появится окно
Residual Analysis (Рис. 3.20).
53
Рис. 3.20
•
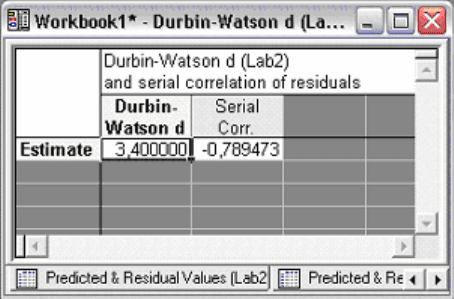
в закладке Advanced нажмите Summary: Residuals & predicted
для анализа остатков (Рис. 3.21).
Рис. 3.21
•
затем кнопку Durbin-Watson statistic для расчета критерия
Дарбина-Уотсона (Рис. 3.21).
54
Рис. 3.22
•
закройте окно программы STATISTICA.
55
4. ДИСПЕРСИОННЫЙ АНАЛИЗ
“Если достаточно долго
пытать данные, то, в конце
концов, Природа признается”
Рональд Коуз
4.1. ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ
Задачей дисперсионного анализа является изучение влияния одного
или нескольких факторов на рассматриваемый признак.
Однофакторный дисперсионный анализ используется в тех случаях,
когда есть в распоряжении три или более независимые выборки,
полученные из одной генеральной совокупности путем изменения какого-
либо независимого фактора, для которого по каким-либо причинам нет
количественных измерений.
Для этих
выборок предполагают, что они имеют разные выборочные
средние и одинаковые выборочные дисперсии. Поэтому необходимо
ответить на вопрос, оказал ли этот фактор существенное влияние на
разброс выборочных средних или разброс является следствием
случайностей, вызванных небольшими объемами выборок. Другими
словами если выборки принадлежат одной и той же генеральной
совокупности, то разброс данных
между выборками (между группами)
должен быть не больше, чем разброс данных внутри этих выборок (внутри
групп).
Пусть
x
ik
– i – элемент (
k
ni ,1
=
)
k
-выборки ( mk ,1= ), где m –
число выборок,
n
k
– число данных в
k
-выборке. Тогда
x
k
– выборочное
среднее
k
-выборки определяется по формуле
∑
=
=
n
i
ik
k
k
k
x
n
x
1
1
.
Общее среднее вычисляется по формуле
∑∑
=
==
n
i
ik
m
k
k
x
n
x
11
1
, где
.
1
∑
=
=
m
k
k
n
n
Основное тождество дисперсионного анализа имеет следующий вид:
QQ
Q
21
+
=
,
где
Q
1
– сумма квадратов отклонений выборочных средних
k
x
от
общего среднего
x
(сумма квадратов отклонений между группами); Q
2
–
сумма квадратов отклонений наблюдаемых значений
x
ik
от выборочной

56
средней
x
k
(сумма квадратов отклонений внутри групп); Q – общая сумма
квадратов отклонений наблюдаемых значений
x
ik
от общего среднего
x
.
Расчет этих сумм квадратов отклонений осуществляется по
следующим формулам:
,)(
2
11
2
11
2
xn
x
x
x
Q
m
k
n
i
ik
m
k
n
i
ik
kk
−
∑∑∑∑
=−=
====
,)(
2
1
2
1
2
1
xn
x
n
x
x
n
Q
m
k
k
k
m
k
k
k
−
∑∑
=−=
==
,)(
2
1
2
1
2
1
xn
x
n
x
x
n
Q
m
k
k
k
m
k
k
k
−
∑∑
=−=
==
В качестве критерия необходимо воспользоваться критерием
Фишера:
)/(
)1/(
2
1
mn
Q
m
Q
F
−
−
=
.
Если расчетное значение критерия Фишера будет меньше, чем
табличное значение
mnm
F
−− ;1 ;
λ
– нет оснований считать, что независимый
фактор оказывает влияние на разброс средних значений, в противном
случае, независимый фактор оказывает существенное влияние на разброс
средних значений (λ – уровень значимости, уровень риска, обычно для
экономических задач λ=0,05).
Недостаток однофакторного анализа: невозможно выделить те
выборки, которые отличаются от других. Для этой цели необходимо
использовать
метод Шеффе или проводить парные сравнения выборок.
Пример 3.1. Три группы продавцов продавали штучный товар,
расфасованный в различные упаковки. После окончания срока распродажи
был произведен тестовый контроль над случайно отобранными
продавцами из каждой группы (табл. 4.1).
Таблица 4.1
Номер
группы
Число продаж,
которые сделали
продавцы,
x
ik
Общее
количество
продаж
Количество
продавцов, n
k
1 1 3 2 1 0 2 1 10 7
2 2 3 2 1 4 - - 12 5
3 4 5 3 - - - - 12 3
57
Если число выборок m=3, число продаж во всех выборках n=15, то:
.622,215/)121210(
; 43/12
; 4,25/12
; 428,17/10
3
2
1
=++=
==
==
==
x
x
x
x
Если
10492516 161494141491
11
2
=+++++++++++++=
∑∑
==
m
k
n
i
ik
k
x
074,91434,25428,17
222
1
2
=⋅+⋅+⋅=
∑
=
m
k
k
k
x
n
,
тогда
Q=104–15·2,226
2
=26,93 ;
Q
1
=91,074–15·2,226
2
=14,01 ;
Q
2
=Q–Q
1
=26,93–14,01=12,92 .
Вычислим критерий Фишера
.52,6
12/92,12
2/01,14
==F
Сравнивая это значение с табличным
F > F
0,05;2;12
=3,885
(прилож. 1), делаем вывод, что упаковка (особенно красочная!) влияет на
количество распродаж.
4.2. STATISTICA. ПРОВЕРКА РЕЗУЛЬТАТОВ КОНТРОЛЬНОГО
ПРИМЕРА В ANOVA
Рассмотрим процедуру решения рассмотренной задачи методом
дисперсионного анализа в системе
STATISTICA.
•
запустите программу STATISTICA командой
Пуск/Программы/Statistica6.0/Statistica;
•
в открывшемся окне закрыть все окна документов и выполнить
команду
File/New Data. В окне Create New Document указывается число
создаваемых строк и столбцов, по умолчанию создается таблица для ввода
данных размером (10х10);
•
введите исходные данные для переменных в столбцы VAR1 и
VAR2 в следующем виде (придется добавить 5 Cases) (Рис. 4.1).
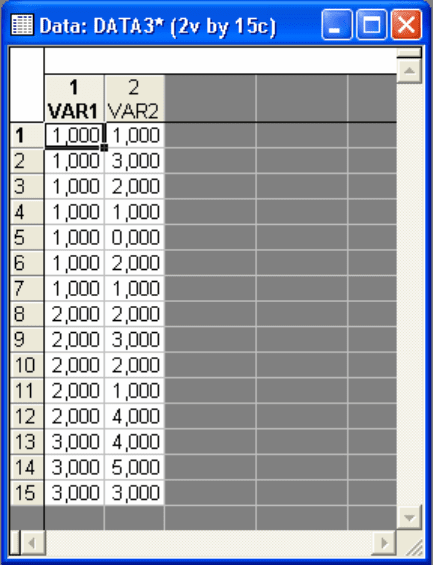
58
Рис. 4.1
•
щелкая правой клавишей по столбцам VAR1 и VAR2, выберите
контекстное меню, выделите пункт
Variable Specs… и поменяйте имена
переменных, если в этом есть необходимость.
•
File/Save As – сохраните полученный файл.
•
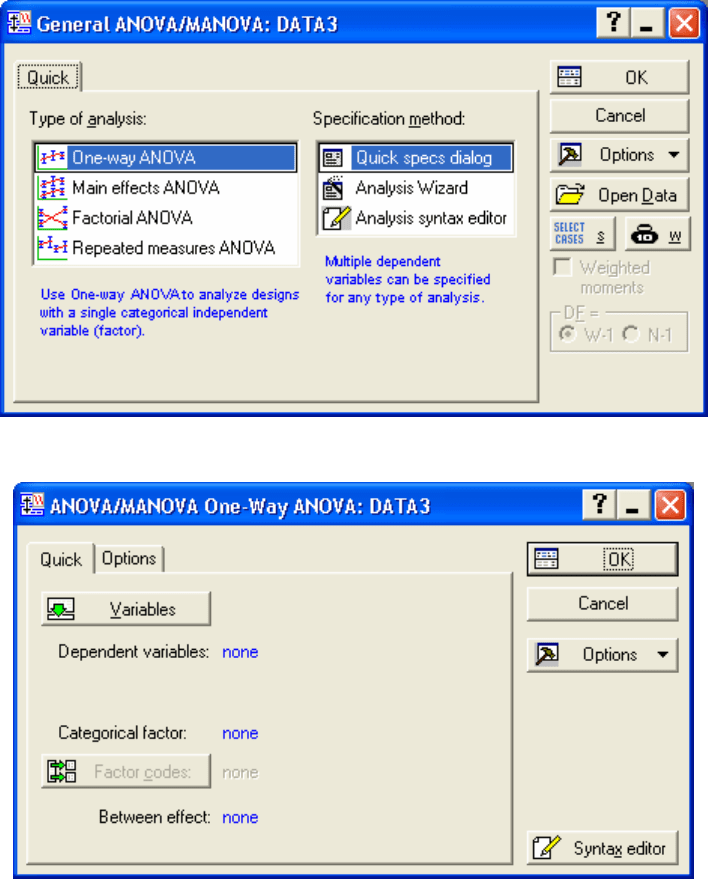
Выберите модуль ANOVA в меню Statistics. Появится диалоговое
окно
General ANOVA/MANOVA. Выберите тип анализа One-way
ANOVA
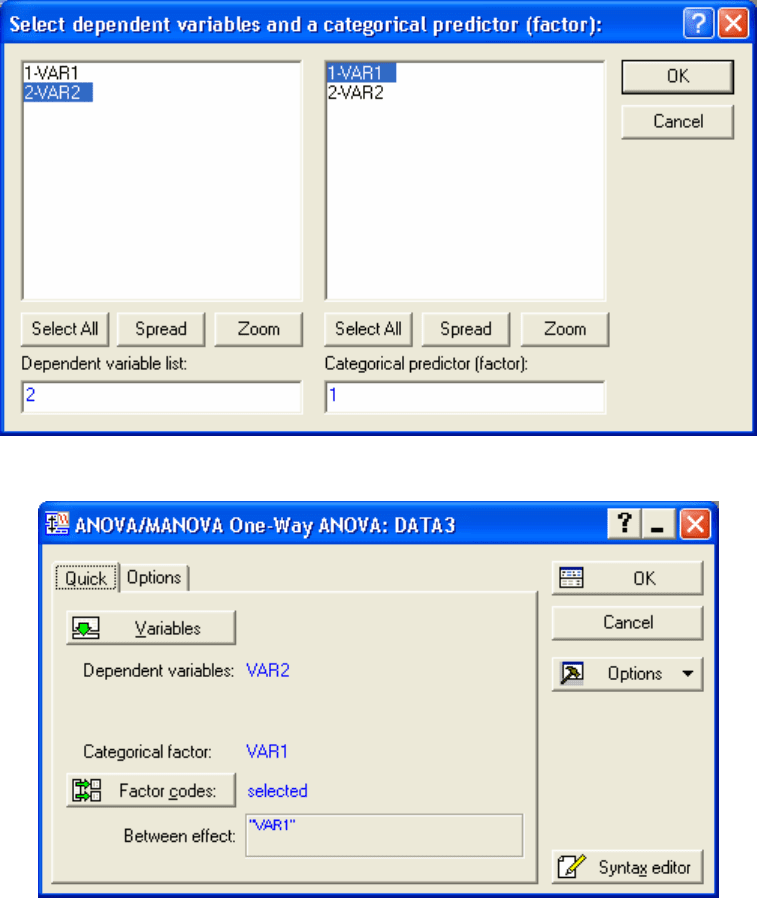
(Рис. 4.2) и нажмите ОК. На панели ANOVA/MANOVA (Рис. 4.3)
нажмите кнопку
Variables и определите категориальный фактор (VAR1) и
зависимую переменную(VAR2) (Рис. 4.4). Далее нажмите
ОК. На
появившейся панели нажмите кнопку
Factor codes и выберите все коды,
добейтесь результата (Рис. 4.5). В данном диалоговом окне нажмите
ОК.
59
Рис. 4.2
Рис. 4.3
60
Рис. 4.4
Рис. 4.5
• для решения данной задачи достаточно нажать кнопку All effects
(Рис. 4.6) и на экране появятся результаты общего дисперсионного анализа
(Рис. 4.7). Если эти результаты выделены красным цветом – фактор
оказывает существенное влияние, что мы и наблюдаем на экране. Более
точный вывод можно сделать, применив критерий Фишера.
