Labelle P. Supersymmetry DeMYSTiFied
Подождите немного. Документ загружается.


386
Supersymmetry Demystified
the origin along the line x = y, this term vanishes, and we must be more careful.
In this case, the potential reduces to
V
n
(x = y) = (a
1
+ a
2
− 2b)x
2
This is a parabola. If we want this to have a minimum (as opposed to a maximum),
the overall coefficient must be positive. This implies that a
1
+ a
2
> 2b. And since
b is itself larger or equal to zero, we have
a
1
+ a
2
> 2b ≥ 0 (16.11)
Recalling the definitions in Eq. (16.7), this translates into
2|μ|
2
+ δm
2
H
u
+ δm
2
H
d
> 2b > 0
There are three possibilities:
•
Both a
1
and a
2
are positive with a
1
+ a
2
> 2b
•
a
1
is positive and a
2
negative with a
1
> 2b +|a
2
|
•
a
1
is negative and a
2
positive with a
2
> 2b +|a
1
|
Now that we have ensured that the potential goes to infinity in any direction, we
also want to ensure that the origin, x = y = 0, is not a minimum because then the
vev of all the fields would be zero, and there would be no spontaneous symmetry
breaking of the gauge symmetry. We already know that along the line y = x,we
have a minimum at the origin. The only way for the origin not to be a minimum of
the potential (along any direction) is to impose it to be a saddle point at the origin,
which leads to the condition
∂
2
V
n
∂x
2
∂
2
V
n
∂x∂ y
∂
2
V
n
∂x∂ y
∂
2
V
n
∂y
2
x=y=0
< 0
which leads to the condition
a
1
a
2
< b
2
(16.12)
or, equivalently,
|μ|
2
+ δm
2
H
u
|μ|
2
+ δm
2
H
d
|
< b
2

CHAPTER 16 Phenomenological Implications
387
To summarize, conditions (16.11) and (16.12) are required in order for our
potential to have a minimum and for that minimum to not be at the origin.
Let us now assume that both conditions are satisfied and look for a minimum
with nonzero values of x and y. Recall that x denotes H
0
u
and y represents H
0
d
,so
let us call the coordinates of the minimum x
min
≡ v
u
and y
min
≡ v
d
. So we impose
∂V
n
∂x
x=v
u
,y=v
d
=
∂V
n
∂y
x=v
u
,y=v
d
= 0
This gives the two conditions
a
1
v
u
− bv
d
+ 2cv
u
v
2
u
− v
2
d
= 0
a
2
v
d
− bv
u
− 2cv
d
v
2
u
− v
2
d
= 0 (16.13)
Thus, at this point, we have seven independent parameters: the five parameters
of the scalar potential [see Eq. (16.8)], which are a
1
, a
2
, b, c, and g, and the two
vevs v
u
and v
d
. As constraints, we have the two equalities (16.13) as well as the two
inequalities, (16.11) and (16.12). We will soon come back to these constraints, but
first, let us find what the masses of the gauge bosons can tell us about our parameters.
16.4 The Masses of the Gauge Bosons
Calculation of the gauge boson masses proceeds along exactly the same lines as in
the standard model (see Section 15.2). The MSSM lagrangian contains the following
kinetic terms for the Higgs scalars:
(D
μ
H
u
)
†
(D
μ
H
u
) + (D
μ
H
d
)
†
(D
μ
H
d
) (16.14)
where
D
μ
= ∂
μ
+ig
τ ·
W
μ
2
+i
g
2
YB
μ
= ∂
μ
+
ig
2
⎛
⎜
⎝
W
3
W
1μ
−iW
2μ
W
1μ
+iW
2μ
−W
3μ
⎞
⎟
⎠
+
ig
Y
2
B
μ
⎛
⎜
⎝
10
01
⎞
⎟
⎠
(16.15)

388
Supersymmetry Demystified
Recall that
H
u
=
⎛
⎝
H
+
u
H
0
u
⎞
⎠
At the minimum of the potential, this becomes
H
u
=
⎛
⎝
0
v
u
⎞
⎠
Similarly, H
d
at the minimum of the potential is
H
d
=
⎛
⎝
v
d
0
⎞
⎠
Using the fact that the hypercharge of H
u
is equal to 1, we get
D
μ
⎛
⎝
0
v
u
⎞
⎠
=
ig
2
v
u
⎛
⎝
W
1μ
−iW
2μ
−W
3μ
⎞
⎠
+
ig
2
v
u
B
μ
⎛
⎝
0
1
⎞
⎠
and using the fact that H
d
has a hypercharge of −1,
D
μ
⎛
⎝
v
d
0
⎞
⎠
=
ig
2
v
d
⎛
⎝
W
3μ
W
1μ
+iW
2μ
⎞
⎠
−
ig
2
v
d
B
μ
⎛
⎝
1
0
⎞
⎠
Inserting these expressions in Eq. (16.14), we get the following contribution to
the masses of the gauge bosons:
L
MGB
=
g
2
4
v
2
u
+ v
2
d
W
1μ
W
μ
1
+ W
2μ
W
μ
2
+ W
3μ
W
μ
3
−
gg
2
v
2
u
+ v
2
d
W
3μ
B
μ
+
g
2
4
v
2
u
+ v
2
d
B
μ
B
μ
We expect to be able to rewrite this in a form similar to Eq. (15.13), and indeed,
we can reorganize the terms to get
L
MGB
=
g
2
4
v
2
u
+ v
2
d
W
2
1
+ W
2
2
+
v
2
u
+ v
2
d
4
g
2
W
2
3
− 2gg
W
3μ
B
μ
+ g
2
B
2
=
g
2
4
v
2
u
+ v
2
d
W
2
1
+ W
2
2
+
v
2
u
+ v
2
d
4
(gW
3
− g
B)
2
(16.16)

CHAPTER 16 Phenomenological Implications
389
Following exactly the same steps as in Section 15.2, we get the same expressions
for the W
±
, Z, and A
μ
(photon fields) with masses now given by
m
2
W
=
g
2
2
v
2
u
+ v
2
d
m
2
Z
= (g
2
+ g
2
)
v
2
u
+ v
2
d
2
and, of course, the mass of the photon being zero. We see that these relations are
exactly the same as in the standard model with v
2
replaced by v
2
u
+ v
2
d
. Let us define
v
2
susy
≡ v
2
u
+ v
2
d
so that the relations for the gauge boson masses have exactly the same form as in
the standard model with v
2
replaced by v
2
susy
. Note that
c =
m
2
Z
4v
2
susy
(16.17)
In addition, studying the weak interaction at low energies yields of course, the
same relation with Fermi’s constant as in the standard model [Eq. (15.15)]. Using
those results, we see that the parameters g, g
, and the combination v
susy
are all
fixed by experiments and have the same values as in the standard model. It is
customary to trade the parameters g and g
(and therefore c) for v
susy
and the gauge
boson masses m
W
and m
Z
, so we will take our seven parameters to be
m
Z
, m
W
, v
susy
, a
1
, a
2
, b
plus any combination of v
u
and v
d
that is linearly independent of v
2
susy
. As we will
see below, the ratio v
u
/v
d
proves convenient.
We now turn our attention to the two conditions (16.13) and the two inequalities
(16.11) and (16.12). Let us first go back to Eq. (16.13). The first one is
a
1
v
u
− bv
d
+ 2cv
u
v
2
u
− v
2
d
= 0
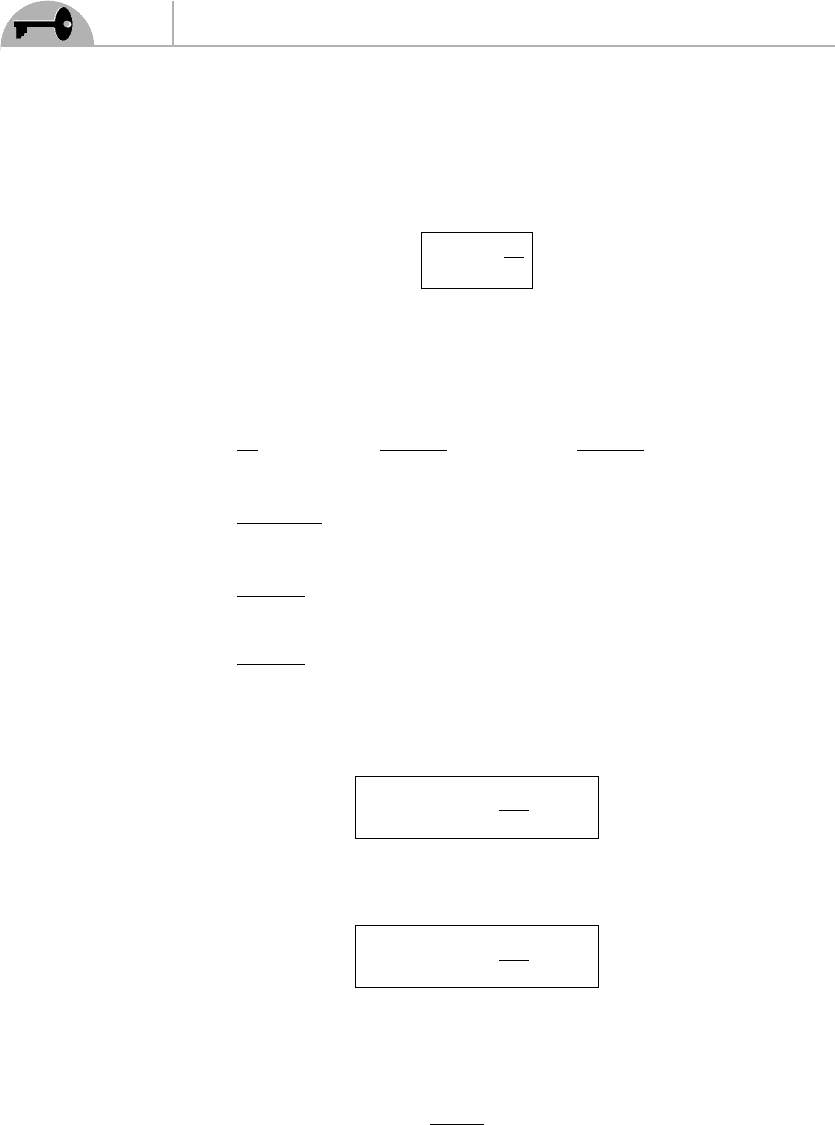
Isolating a
1
, we get [using Eq. (16.17)]
a
1
= b
v
d
v
u
− 2c
v
2
u
− v
2
d
= b
v
d
v
u
−
v
2
u
− v
2
d
v
2
u
+ v
2
d
m
2
Z
2
390
Supersymmetry Demystified
Note that it might seem at first sight that a
1
depends on four parameters, but actu-
ally, it depends only on three because v
u
and v
d
only appear in the ratio v
u
/v
d
. Thus
we can rewrite a
1
in terms of only three parameters: b, m
Z
, and the dimensionless
ratio v
u
/v
d
. Let us define
tan β ≡
v
u
v
d
Since v
u
and v
d
are real and positive quantities, 0 ≤ β ≤ π/2. All expressions that
depend only on the ratio v
u
/v
d
can be expressed in terms of the angle β.Afew
useful relations are
v
d
v
u
= cot β
v
2
u
v
2
u
+ v
2
d
= sin
2
β
v
2
d
v
2
u
+ v
2
d
= cos
2
β
v
2
u
− v
2
d
v
2
u
+ v
2
d
= sin
2
β − cos
2
β =−cos 2β
v
2
d
− v
2
u
v
u
v
d
= cot β − tan β = 2 cot 2β
v
2
u
+ v
2
d
v
u
v
d
= tan β + cot β = 2 cosec 2β (16.18)
We therefore finally get
a
1
= b cot β +
m
2
Z
2
cos 2β
(16.19)
Similarly, we find [still using Eqs. (16.13), (16.17) and (16.18)]
a
2
= b tan β −
m
2
Z
2
cos 2β
(16.20)
Let’s now turn our attention to the inequalities (16.11) and (16.12). Using the
preceding expressions for a
1
and a
2
, Eq. (16.11) translates into
1
sin 2β
> 1

CHAPTER 16 Phenomenological Implications
391
This is satisfied at the condition that β = π/4, or in other words, the two vevs v
u
and v
d
must not be equal:
v
u
= v
d
(16.21)
The inequality (16.12) leads to the condition
b
2
− m
2
Z
b cos(2β) cot 2β −
m
4
Z
4
cos
2
(2β) < b
2
which implies
m
2
Z
b cos(2β) cot 2β +
m
2
Z
4
cos
2
(2β) > 0
Since b ≥ 0 and β ≤ π/2, this is always satisfied except at β = π/4, once more.
Thus we get again the condition (16.21).
To summarize, we started this section with seven parameters: a
1
, a
2
, b, m
Z
, m
W
,
and v
2
susy
and any combination of v
u
and v
d
independent of v
2
susy
. We have seen
that it proves convenient to choose for this combination the ratio v
u
/v
d
, which can
be expressed in terms of the angle β. We then used the constraints on the vevs
to eliminate a
1
and a
2
in terms of the other parameters. We therefore have five
parameters left:
m
2
W
, m
2
Z
, v
2
susy
, b,β
Of these, the first three are determined experimentally, leaving us with two free
parameters with only the constraint β = π/4.
It turns out that when we determine the masses of the Higgs bosons, we will be
able to express everything in terms of only four of these parameters: m
Z
, m
W
, β,
and b; the parameter v
2
susy
will play no role.
Note that all our results are only valid at tree level. Therefore the restriction
β = π/4 (and therefore v
u
= v
d
) should not be seen as exact. In any case, it makes
more sense to ignore it given that an incredible fine-tuning would be required
for the vevs to correspond to the only point of parameter space that needs to be
excluded! We won’t discuss loop corrections except for a small comment at the end
of Section 16.5.
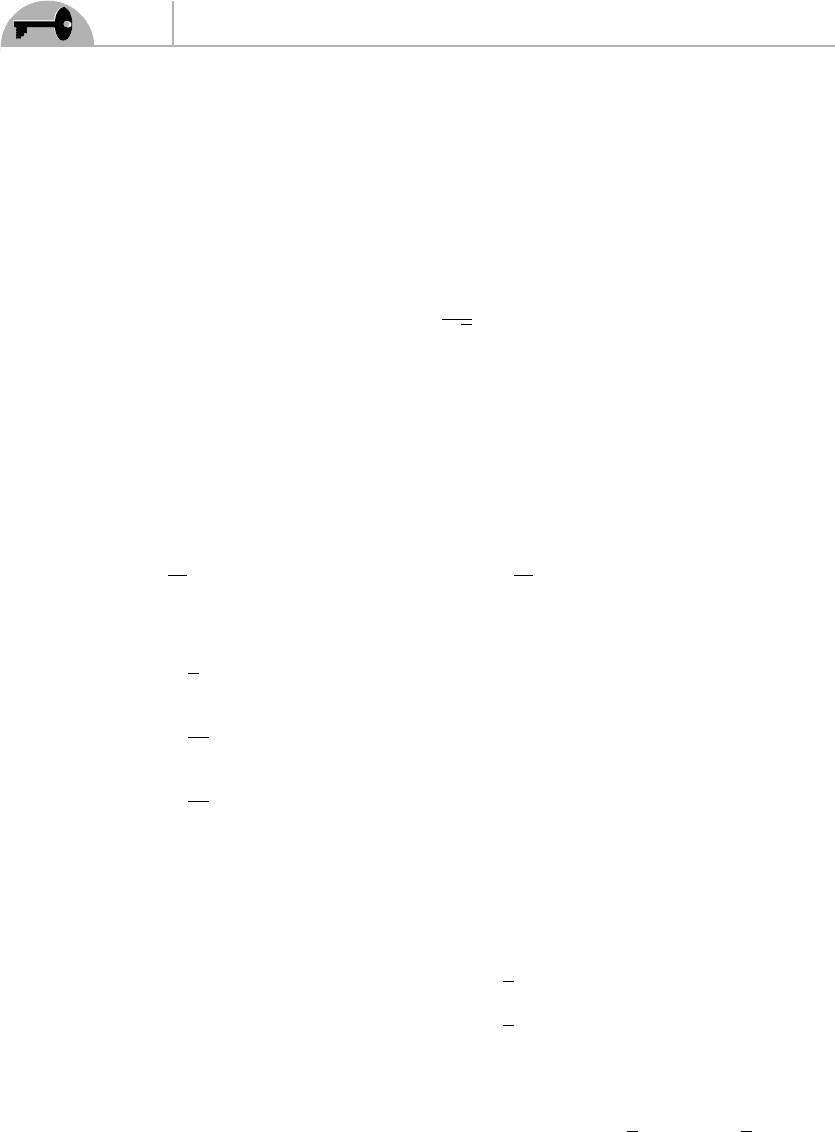
392
Supersymmetry Demystified
16.5 Masses of the Higgs
It is important to keep in mind that the four scalar fields (H
0
u
, H
+
u
, H
0
d
, H
0
d
) are
all complex, so there are eight degrees of freedom. To make this explicit, it is
convenient to express all the fields in terms of their real and imaginary parts. To
simplify our calculations, we will use the notation
H
0
u
=
1
√
2
R
0
u
+iI
0
u
where
R
0
u
≡ Re
H
0
u
I
0
u
≡ Im
H
0
u
and so on. The complete Higgs potential (not evaluated at the minimum) given in
Eq. (16.8) then takes the form
V =
a
1
2
R
+
u
2
+
I
+
u
2
+
R
0
u
2
+
I
0
u
2
+
a
2
2
R
0
d
2
+
I
0
d
2
+
R
−
d
2
+
I
−
d
2
+b
R
+
u
R
−
d
− I
+
u
I
−
d
− R
0
u
R
0
d
+ I
0
u
I
0
d
+
c
4
R
+
u
2
+
I
+
u
2
+
R
0
u
2
+
I
0
u
2
−
R
0
d
2
−
I
0
d
2
−
R
−
d
2
−
I
−
d
2
2
+
g
2
8
R
0
d
R
+
u
+ I
0
d
I
+
u
+ R
−
d
R
0
u
+ I
−
d
I
0
u
2
+
g
2
8
R
0
d
I
+
u
− I
0
d
R
+
u
− I
−
d
R
0
u
+ I
0
u
R
−
d
2
(16.22)
We have not expressed a
1
and a
2
and g and c in terms of v
susy
, m
W
, m
Z
,β, and
b because this makes the intermediate calculations cumbersome. We will change
parameters when we express our final results for the Higgs masses.
The only fields with a nonzero vev are R
0
u
and R
0
d
:
*
R
0
u
+
=
√
2v
u
*
R
0
d
+
=
√
2v
d
To work out the masses of all the Higgs fields, we proceed as in Section 14.4: We
take the second derivative of the potential with respect to all the Higgs fields and
evaluate the resulting expression at the minimum, R
0
u
=
√
2v
u
, R
0
d
=
√
2v
d
and all
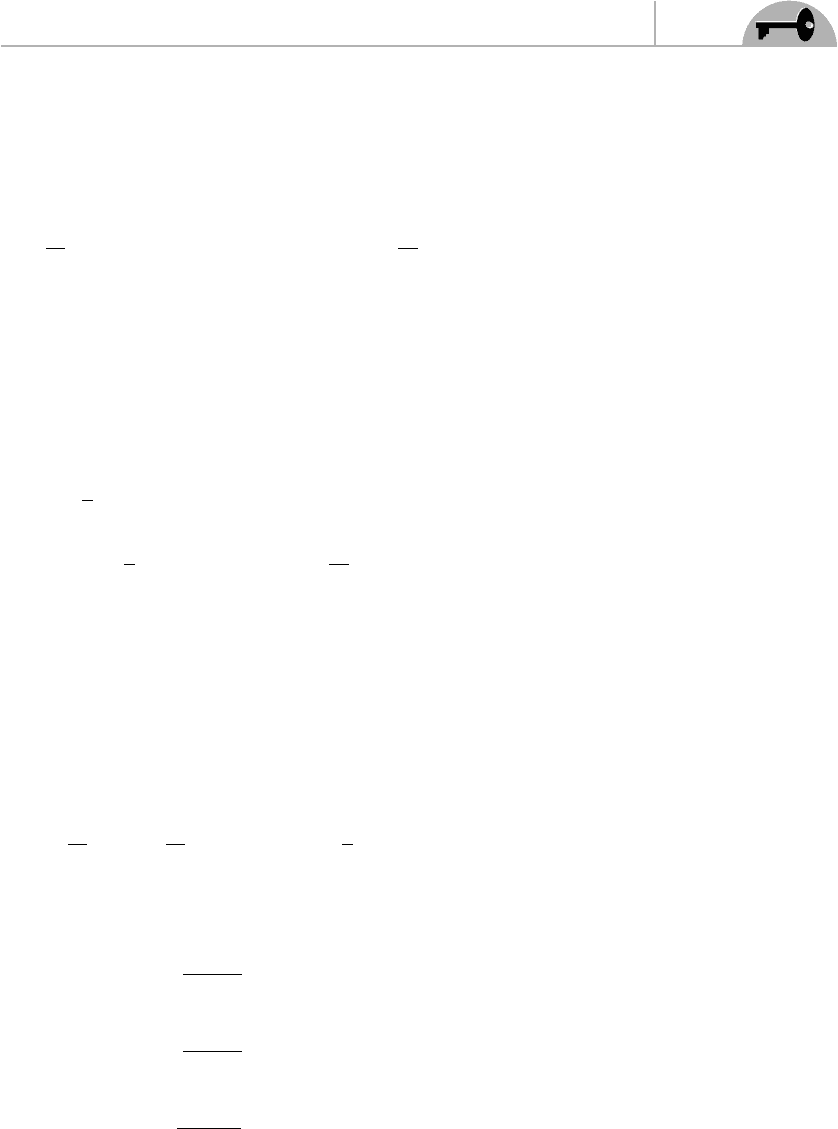
CHAPTER 16 Phenomenological Implications
393
the other fields set to zero. Only a fraction of the terms appearing in Eq. (16.22)
survive when we do that. They can be grouped into three categories:
•
The terms quadratic in a field. These are
a
1
2
R
+
u
)
2
+
I
+
u
2
+
R
0
u
2
+
I
0
u
2
+
a
2
2
R
0
d
2
+
I
0
d
2
+
R
−
d
2
+
I
−
d
2
•
The terms containing the product of two different fields. These are
b
R
+
u
R
−
d
+ I
0
u
I
0
d
− R
0
u
R
0
d
− I
+
u
I
−
d
•
The quadratic terms that have at least two fields that are either R
0
u
or R
0
d
. These
are
c
2
&
R
0
u
2
−
R
0
d
2
'&
R
+
u
2
+ I
+2
u
+ I
02
u
− I
02
d
− R
−2
d
− I
−2
d
'
+
c
4
&
R
0
u
2
−
R
0
d
2
'
2
+
g
2
8
&
R
+
u
2
R
0
d
2
+
R
0
u
2
R
−
d
2
+2R
+
u
R
0
d
R
0
u
R
−
d
+
I
+
u
2
R
0
d
2
+
R
0
u
2
R
0
u
2
I
−
d
2
− 2I
+
u
I
−
d
R
0
u
R
0
d
'
All the other terms will not contribute once we take the second derivatives with
respect to the fields and set them equal to their vevs.
We see that there is a mixing of masses between the pairs (I
0
u
, I
0
d
), (R
0
u
, R
0
d
),
(R
+
u
R
−
d
), and (I
+
u
, I
−
d
), so we will consider each pair separately.
Consider first the pair (I
0
u
, I
0
d
). The relevant terms are
a
1
2
I
0
u
2
+
a
2
2
I
0
d
2
+ bI
0
u
I
0
d
+
c
2
&
R
0
u
2
−
R
0
d
2
'&
I
0
u
2
−
I
0
d
2
'
So we get [using Eqs. (16.17) to (16.20)]
∂
2
V
∂
I
0
u
2
vev
= a
1
+ 2c
v
2
u
− v
2
d
= b cot β
∂
2
V
∂
I
0
d
2
vev
= a
2
− 2c
v
2
u
− v
2
d
= b tan β
∂
2
V
∂ I
0
u
∂ I
0
d
vev
= b
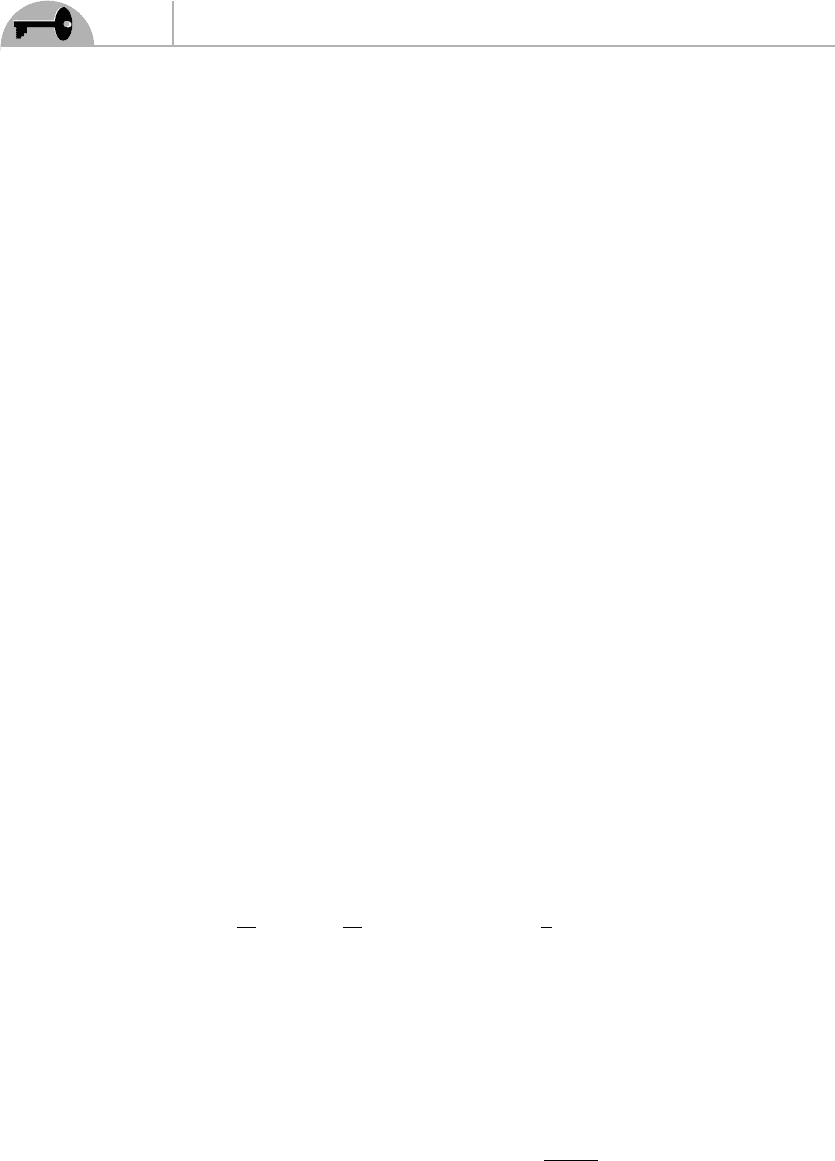
394
Supersymmetry Demystified
where the subscript vev means that all the fields are set equal to their vacuum
expectation value. The squared mass matrix is then
V = b
⎛
⎜
⎝
cot β 1
1 tan β
⎞
⎟
⎠
The squared masses are given by the solutions of
λ
2
− λb
tan(β) + cot(β)
= 0 (16.23)
which are
0 and 2 b cosec(2β)
The massless state provides the longitudinal mode of the Z
0
, following the same
mechanism as in the standard model. Following a standard practice, we will denote
the field corresponding to the massive state by A
0
, which has, therefore, a mass
squared:
m
2
A
0
≡ 2 b cosec(2β) (16.24)
We can use this relation to trade the parameter b for the mass m
A
0
, so that our five
parameters are now
m
W
, m
Z
, v
SUSY
,β, and m
A
0
(16.25)
We won’t work out the explicit mass eigenstates, i.e., the linear combinations of I
0
u
and I
0
d
, that correspond to these masses.
Since in principle β can be very small, there is no upper limit on this mass.
Next, consider the fields R
0
u
and R
0
d
. The relevant terms are
a
1
2
R
0
u
2
+
a
2
2
R
0
d
2
− bR
0
u
R
0
d
+
c
4
&
R
0
u
2
−
R
0
d
2
'
2
This time, we find the squared mass matrix to be more complicated. We get (on the
basis of R
0
u
, R
0
d
)
V
11
= a
1
+
6 v
2
u
− 2 v
2
d
c = b cot β + sin
2
(β) m
2
Z
V
22
= a
2
+
6 v
2
d
− 2 v
2
u
c = b tan β + cos
2
(β) m
2
Z
V
12
= V
21
=−4 v
u
v
d
c − b =−
sin 2β
2
m
2
Z
− b (16.26)

CHAPTER 16 Phenomenological Implications
395
We must find the eigenvalues of the matrix
V =
⎛
⎜
⎝
b cot β + sin
2
(β)m
2
Z
−
sin(2β)
2
m
2
Z
− b
−
sin(2β)
2
m
2
Z
− bbtan β + cos
2
(β) m
2
Z
⎞
⎟
⎠
which can be shown to be
b sec 2β +
m
2
Z
2
±
1
2
)
(2 b cot 2β + m
2
Z
cos(2β))
2
+ 4(sin(2β)m
2
Z
/2 + b)
2
(16.27)
The Higgs fields corresponding to those two masses are referred to as the H
0
[when
the plus sign is used in Eq. (16.27)] and the h
0
(when the minus sign is used). The
expression for the masses simplifies tremendously if we express b in terms of m
A
0
using Eq. (16.24), which leads to
m
2
A
0
+ m
2
Z
2
±
1
2
)
m
2
A
0
− m
2
Z
2
cos
2
2β +
m
2
A
0
+ m
2
Z
2
sin
2
2β
Writing sin
2
2β as 1 − cos
2
2β, we finally get the two masses to be
m
2
h
0
=
m
2
A
0
+ m
2
Z
2
−
1
2
)
m
2
A
0
+ m
2
Z
2
− 4 m
2
A
0
m
2
Z
cos
2
2β
and
m
2
H
0
=
m
2
A
0
+ m
2
Z
2
+
1
2
)
m
2
A
0
+ m
2
Z
2
− 4 m
2
A
0
m
2
Z
cos
2
2β (16.28)
Consider now the pair (R
+
u
R
−
d
). The relevant terms in the lagrangian are
a
1
2
R
+
u
2
+
a
2
2
R
−
d
2
+ bR
+
u
R
−
d
+
c
2
&
R
0
u
2
−
R
0
d
2
'&
R
+
u
2
−
R
−
d
2
'
+
g
2
8
&
R
+
u
2
R
0
d
2
+
R
0
u
2
R
−
d
2
+ 2R
+
u
R
0
d
R
0
u
R
−
d
'
