Кузюрин Н.Н. Фомин С.А. Эффективные алгоритмы и сложность вычислений

Подождите немного. Документ загружается.

1.1. Примеры задач и алгоритмов 51

самым входной интервал на интервалы длины k − 1 и N − k.

Тогда можно записать следующую рекурсивную оценку мате-

матического ожидания сложности алгоритма:

T (N) = O(N) +

k=1

(T (k − 1) + T (N − k))

= O(N) +

N−1

k=1

T (k). (1.3)

Проверим разумную гипотезу, что

T (N) = O(N log N), (1.4)

т. е. что ∃C : T (N) ≤ CN log N.

Действительно (логарифм двоичный):

N−1

k=1

k log k ≤ log N ·

(1.5)

Подставляя (1.5) в (1.3), убеждаемся, что T (N ) = CN log N

для некоторой константы C.

Однако допущенное нами предположение о равномерности

распределения «осей» относительно интервалов может не вы-

полняться на практике. На практике возможна ситуация, ко-

гда для выбранной функции «pivotFunc» будут попадаться ис-

ключительно «плохие» входные данные. В таком случае, когда

нельзя «сделать случайными» входные данные, можно внести

элемент случайности непосредственно в сам алгоритм. В част-

ности, чтобы сохранилась оценка математического ожидания

(1.4), достаточно сделать вероятностным выбор осевого элемен-

та из разделяемого интервала — см. использование функции

«pivotRandom» на рис. 1.5.

Другие интересные примеры анализа поведения алгорит-

мов на случайных данных будут рассмотрены в главе 3.

52 Глава 1. Алгоритмы и их сложность

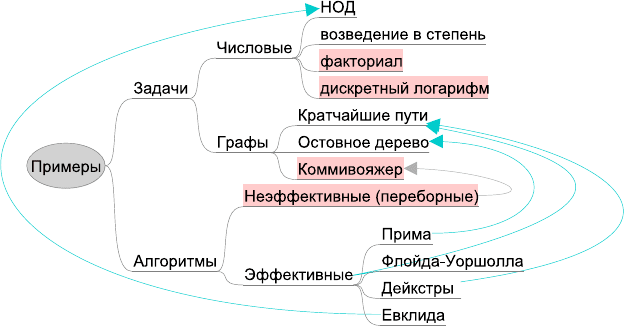
В завершение раздела приведем небольшую «карту памя-

ти» для запоминания рассмотренных в разделе понятий.

Рис. 1.6. Карта-памятка раздела 1.1

1.2. Формально об алгоритмах. Несложно

о сложности

1.2.1.



RAM



: машины с произвольным доступом

При написании данного раздела использован обзор [96].

В предыдущих разделах мы довольствовались качествен-

ным, интуитивным понятием «эффективного» алгоритма. Для

построения же математической теории сложности алгоритмов,

разумеется, необходимо строгое количественное определение

меры эффективности.

Опыт, накопленный в теории сложности вычислений, сви-

детельствует, что наиболее удобным и адекватным способом

сравнения эффективности разнородных алгоритмов является

понятие асимптотической сложности, рассмотрению которо-

го и посвящен настоящий параграф.

1.2. Формально об алгоритмах. Несложно о сложности 53

Первое, о чем следует договориться, — это выбор вычис-

лительной модели, в которой конструируются наши алгорит-

мы. Оказывается, что как раз этот вопрос не имеет слишком

принципиального значения для теории сложности вычислений,

и тот уровень строгости, на котором мы работали в разделе 1.1

(число выполненных операторов на языке Python), оказывает-

ся почти приемлемым. Главная причина такого легкомыслен-

ного отношения к выбору модели состоит в том, что существу-

ют весьма эффективные способы моделирования (или транс-

ляции программ в более привычных терминах) одних есте-

ственных вычислительных моделей с помощью других. При

этих моделированиях сохраняется класс эффективных алго-

ритмов и, как правило, алгоритмы более эффективные в одних

моделях оказываются более эффективными и в других.

Сначала рассмотрим модель, наиболее напоминающую со-

временный компьютер, программируемый непосредственно

в терминах инструкций процессора (или на языке Assembler):

random access machines (RAM)

, т. е. «машины с произволь-

ным доступом к памяти».

RAM-машину составляют следующие компоненты (рис. 1.7).

• Конечная входная read-only лента, на которую записыва-

ются входные данные.

• Полубесконечная

выходная write-only лента, куда запи-

сывается результат работы машины.

• Бесконечное число регистров r

, r

, . . ., каждый из ко-

торых может хранить произвольное целое число (изна-

чально везде записаны нули). Регистр r

является выде-

ленным и называется «сумматором» — этот регистр ис-

В теории сложности вычислений под машинами традиционно пони-

мают single-purpose machines, т. е. машины, каждая из которых создана

для решения какой-либо одной фиксированной задачи. В привычных тер-

минах это скорее программы.

Ограниченная с одной стороны и неограниченная с другой.

54 Глава 1. Алгоритмы и их сложность

пользуется при арифметических операциях как накопи-

тель, т. е. как второй операнд и место хранения результа-

та.

• Программа, состоящая из конечного числа инструк-

ций, каждая из которых содержит адрес и команду

с операндом. Список команд приведен в таблице 1.2.

Существенно, что в качестве операнда можно использо-

вать как произвольный регистр, так и регистр, номер

которого хранится в другом регистре — это так называе-

мая косвенная адресация.

• Регистр-счетчик «PC» — указатель текущей команды.

Машина последовательно, такт за тактом, выполняет ко-

манды, на которые указывает регистр «PC», читает входную

ленту, изменяет значения регистров и записывает результат на

выходную ленту.

Легко видеть, что высокоуровневые конструкции языков

программирования, типа циклов, легко моделируются на ас-

семблере RAM-машин (см. рис. 1.8).

Переменные других типов (булевы, строки, структуры) то-

же можно моделировать с помощью целых чисел и косвенной

адресации.

Обратите внимание, что, несмотря на «примитивный ассем-

блер», RAM-машины потенциально мощнее любых существу-

ющих компьютеров и физически нереализуемы, т.к. опериру-

ют бесконечной памятью, где доступ к любой ячейке-регистру

осуществляется мгновенно при выполнении соответствующей

инструкции, и каждая ячейка этой памяти может содержать

произвольное целое число (т. е. не ограничена по размеру).

Но эта модель уже дает возможность вводить более или ме-

нее формальные определения времени выполнения программы

(как число тактов до остановки машины) и, соответственно,

сложности алгоритма.

1.2. Формально об алгоритмах. Несложно о сложности 55

Т а б л и ц а 1.2

RAM-машина: Список команд

LOAD OP r

← OP Загрузить операнд

в сумматор.

STORE OP r

← r

Сохранить сумматор

в регистре.

ADD OP r

← r

+ OP Прибавить операнд

к сумматору.

SUB OP r

← r

− OP Вычесть операнд из сум-

матора.

READ OP r

← input Загрузить ячейку из

входной ленты в r

и перейти к следующей.

WRITE OP OP → output Записать OP в текущую

ячейку выходной ленты

и сдвиг к следующей.

JUMP OP P C ← OP Установить счетчик ко-

манд в OP .

JGTZ OP P C ← OP : r

> 0 Установить счетчик ко-

манд в OP , если r

> 0.

JZERO OP P C ← OP : r

= 0 Установить счетчик ко-

манд в OP , если r

= 0.

HALT Остановить работу.

Операнд OP может быть:

• целым числом, например, 7, −1917;

• регистром, например, r

, r

;

• значением регистра, указанного в другом регистре.

Например, операнд ∗r

означает значение регистра,

номер которого указан в регистре r

56 Глава 1. Алгоритмы и их сложность

Program Counter

RAM–Program

входная read-only лента

выходная write-only лента



0: LOAD r1

1: ADD 3

2: STORE r7

3: LOAD 77

4: STORE ∗r7

5: JUMP 100

. . .

Рис. 1.7. RAM — машина с произвольным доступом

Если мы будем принимать в расчет только число выпол-

ненных команд, то определим так называемые однородные ме-

ры сложности. В англоязычной литературе RAM с однородной

мерой сложности называются unit-cost RAM.

Более реалистично было бы учитывать битовый размер опе-

рандов при выполнении каждой команды. Например, можно

считать, что время выполнения каждой команды есть едини-

ца плюс величина пропорциональная сумме логарифмов зна-

чений операндов

, если они есть (т. е. их суммарной битовой

длине), а общее время работы программы на рассматриваемых

входных данных — суммарное время выполнения всех индиви-

Более корректно логарифм брать от модуля операнда плюс 2, чтобы

логарифм был положительным.

1.2. Формально об алгоритмах. Несложно о сложности 57

...

for i in range( 1..78 ):

тело цикла

...

⇒

...

0777: LOAD 1

0778: STORE r

0779: начало тела цикла

...

1038: конец тела цикла

1039: LOAD 78

1040: SUB r

1041: JGTZ 0779

...

Рис. 1.8. Моделирование циклов для RAM

дуальных команд. Таким образом, мы можем определить раз-

личные логарифмические меры сложности.

Очевидно, логарифмическая сложность всегда больше од-

нородной. С другой стороны, обратите внимание, что опре-

деленная нами RAM-машина не включает в число основных

операций умножение и деление, хотя в литературе такой ва-

риант машин со случайным доступом часто рассматривается.

Допустим, что однородное время работы некоторой машины

с произвольным доступом к памяти без умножения и деления

при работе на входных данных x

, . . . , x

, битовая длина каж-

дого из которых не больше n, равно t. Так как при выполне-

нии любого индивидуального оператора максимальная битовая

длина может возрасти не более чем на 1, в ходе выполнения

всей программы встречаются лишь числа битовой длины не

более (t + n), и, стало быть, логарифмическая сложность пре-

вышает однородную не более чем в 2(t + n) раз. В частности

(см. обсуждение в разделе 1.1), с точки зрения эффективно-

сти однородная и логарифмическая сложности равносильны, и

выбор одной из них в основном определяется внутренней спе-

цификой рассматриваемой задачи.

Если же добавить умножение и деление к списку элемен-

58 Глава 1. Алгоритмы и их сложность

тарных операций, то это исключит равносильность однородной

и логарифмической сложности. Следующий известный способ

быстро переполнить память карманного калькулятора (алго-

ритм 13) имеет однородную сложность порядка (t + 1) и лога-

рифмическую порядка экспоненты — 2

Алгоритм 13. Переполнение памяти из-за умножения

Вход: Натуральное t

R ← 2

for all i ∈ 1..t do

R ← R × R

end for

Алгоритм 14. Простое вычисление R

· R

на RAM

Вход: Натуральные R

, R

Выход: R

× R

R ← 0

for all i ∈ 1..R

R ← R + R

end for

return R

Как показывает обсуждение в разделе 1.1, этот алгоритм

не может считаться эффективным с точки зрения логарифми-

ческой сложности (хотя и по совершенно другим причинам,

нежели переборные алгоритмы), и, чтобы избежать неприят-

ных эффектов такого рода, мы не включаем умножение (и тем

более деление) в список основных операций.

В тех же случаях, когда умножение используется «в мир-

ных целях», его в большинстве случаев можно промодели-

ровать с помощью сложения очевидным образом (см. алго-

ритм 14 «Умножение»).

В заключение можно отметить, что некоторые частные

случаи модели RAM описывают популярные модели вычис-

1.2. Формально об алгоритмах. Несложно о сложности 59

лений — неветвящиеся программы, булевы схемы

(см. раз-

дел 6.4), а сама модель RAM является основой модели, ис-

пользуемой в теории параллельных вычислений — PRAM

(см. раздел 4.3.1).

1.2.2. Сложность в худшем случае

Чаще всего для характеризации сложности алгоритма в каче-

стве основных вычислительных ресурсов рассматривают вре-

мя, затраченное алгоритмом на вычисление, и использованную

память. Понятно, что потребление этих ресурсов может зави-

сеть от размера входных данных.

Значит, сначала надо определить, что понимать под раз-

мером входных данных. По аналогии с однородными и лога-

рифмическими мерами сложности возникают две различные

возможности. Мы можем определить размер данных как раз-

мерность задачи, т. е. число ячеек RAM, занятых входными

данными. Например, размерность задач 4 «TSP», 5 «SPP», рас-

смотренных в разделе 1.1, равна

n(n−1)

(где n — число вершин в

исходном графе). Либо мы можем определить размер входных

данных как суммарную битовую длину записи всех входных

параметров (

1≤i<j≤n

dlog

(|d

|+1)e для вышеупомянутых за-

дач), т. е. число заполненных ячеек на входной ленте MT.

Большинство алгоритмов, рассмотренных нами в разде-

ле 1.1, обладает тем приятным свойством, что время их рабо-

ты относительно однородной меры сложности зависит лишь от

размерности задачи и не зависит от входных значений ячеек.

Более того, тем же свойством будет обладать любой алго-

ритм, все циклы в котором имеют вид:

for i = 1 to ограничитель do,

Boolean circuits.

Parallel RAM.

60 Глава 1. Алгоритмы и их сложность

где ограничитель — некоторая явная функция, зависящая

только от размерности задачи. Мы будем называть алгоритмы

с этим свойством однородными.

Сложность однородного алгоритма — это целочисленная

функция целого аргумента t(n), равная времени его работы

для входных данных размерности n.

К сожалению, эффективность и однородность — требова-

ния, зачастую плохо совместимые между собой, поэтому нам

необходимо иметь меру сложности, пригодную также для неод-

нородных алгоритмов.

Естественная попытка определить сложность неоднород-

ного алгоритма как функцию t(R

, . . . , R

) от всего масси-

ва входных данных при ближайшем рассмотрении оказывает-

ся неудовлетворительной: эта функция несет в себе огромное

количество избыточной информации, с трудом поддается вы-

числению или хотя бы оцениванию в явном виде и позволяет

сравнивать между собой различные алгоритмы лишь в исклю-

чительных случаях. Поэтому, чтобы получить на самом деле

работающее на практике определение сложности, нам необхо-

димо каким-нибудь образом свести эту функцию к функции

одного (или в крайнем случае небольшого числа) целого ар-

гумента (как в случае однородных алгоритмов). Имеются два

принципиально различных подхода к решению этой задачи.

Самый распространенный подход — это рассмотрение

сложности в наихудшем случае. Мы полагаем t(n) равным

max

(

t(R

, . . . , R

)



i=1

dlog

(|R

| + 1)e ≤ n

)

Иными словами, t(n) — это то время работы, которое дан-

ный алгоритм может гарантировать заведомо, если известно,

что суммарная битовая длина входных данных не превыша-

ет n. При этом время работы алгоритма для некоторых (или

даже для «большинства») таких входных данных может быть