Кузюрин Н.Н. Фомин С.А. Эффективные алгоритмы и сложность вычислений

Подождите немного. Документ загружается.

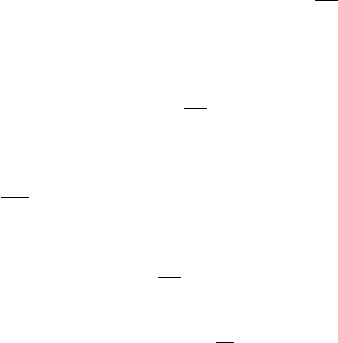
2.1. Алгоритмы с оценками точности 71

Число |J| называется размером минимального покрытия.

Известно, что задача о покрытии N P-полна. По этой при-

чине трудно надеяться на существование полиномиального ал-

горитма точного ее решения.

Рассмотрим алгоритм 15, который действует в соответствии

с простейшей жадной эвристикой: «На каждом шаге выбирать

максимально непокрытое подмножество», т. е. подмножество,

содержащее максимальное число элементов, не покрытых на

предыдущих шагах. Далее мы оценим гарантируемую им точ-

ность.

Теорема 2.1.1. Алгоритм 15 гарантирует точность 1+ln m

для задачи 10 «Set Cover».

Доказательство. Пусть,

— число непокрытых элементов после k-го шага.

M = |J| — размер минимального покрытия.

Так как на любом шаге k, X

непокрытых элементов мы

можем «накрыть» минимальным покрытием размера M, при

этом обязательно будет подмножество, которое накроет

непокрытых элементов (иначе будет противоречие — мини-

мальное покрытие не сможет накрыть X

непокрытых элемен-

тов, и, следовательно, и полное множество тоже). Значит, жад-

ный алгоритм на k-м шаге накроет не менее

непокрытых

элементов, и получится

k+1

≤ X

−

= X

(1 − 1/M). (2.1)

≤ m(1 − 1/M)

≤ m exp



−



Найдем наибольшее k

, при котором m exp



−



≥ 1.

72 Глава 2. Аппроксимация с гарантированной точностью

Алгоритм 15. Жадный алгоритм для задачи о покрытии

«Каждый раз выбирать максимально непокрытое подмноже-

ство».

На рисунке столбцы соответствуют элементам множества,

строки — подмножествам. т. е. каждый графический объект

с координатами x, y представляет принадлежность некоторого

элемента x подмножеству y. Показаны фазы работы жадного

алгоритма — темным цветом выделены выбранные алгоритмом

подмножества.

2.1. Алгоритмы с оценками точности 73

Тогда при k

= k

+ 1 выполнено X

< 1, что означает,

что все элементы покрыты. При этом k

/M ≤ 1 + ln m, значит,

размер покрытия, построенного жадным алгоритмом, превос-

ходит минимальное не более чем в 1 + ln m раз.

Упражнение 2.1.1. Докажите неравенство (2.1).

Упражнение 2.1.2. Постройте пример, где оценка O(1+ln m)

мультипликативной ошибки жадного алгоритма достигается по

порядку. Указание: достаточно рассмотреть случай, когда раз-

мер минимального покрытия M = 2.

Упражнение 2.1.3. Постройте пример, где оценка 1 + ln m

достигается асимптотически.

Встречаются и другие оценки точности жадного алгорит-

ма. Доказано, например (см. [Joh73]), что мультипликативная

ошибка жадного алгоритма не превосходит

1 +

+ . . . +

Асимптотически это выражение как раз равно ln m. Более

точная оценка получена в [Sla96], где доказано, что муль-

типликативная ошибка жадного алгоритма не превосходит

ln m − ln ln m + O(1).

Возникает законный вопрос: а насколько хороши получен-

ные оценки? Достижимость оценки означает лишь, что мы до-

статочно точно оценили ошибку жадного алгоритма. Однако

вполне возможно существование других полиномиальных ал-

горитмов с лучшими оценками. Вопрос этот на самом деле яв-

ляется непростым, и только относительно недавно на него уда-

лось дать удовлетворительный ответ [Fei98].

Оказалось, что при разумных теоретико-сложностных

предположениях, а именно N P 6⊂ DT IME(n

O(log log n)

)

, ни-

какой полиномиальный алгоритм для задачи о покрытии не

См. определения 6.2.4 на стр. 227 и 6.1.7 на стр. 218.

74 Глава 2. Аппроксимация с гарантированной точностью

может иметь мультипликативную ошибку меньше (1 − δ) ln m

для любого фиксированного δ > 0.

Все это является следствием так называемой PCP-теоремы

и ее связями с неаппроксимируемостью (см. теорему 6.3.15 «PCP-

theorem»).

Но, с другой стороны, существует ряд классических раз-

новидностей задачи о покрытии с лучшими оценками ап-

проксимации. Например, «максимизационный» вариант за-

дачи 10 «Set Cover».

Задача 11. «K-покрытие»

Задано:

• Множество X, |X| = m.

• Семейство подмножеств {S

, . . . , S

}, S

⊆ X.

Выбрать такие k подмножеств, чтобы мощность их объеди-

нения была максимальна:

| ∪

j∈J

| → max,

J ⊆ {1, 2, . . . , n},

|J| = k.

Оказалось, жадный алгоритм дает хорошие результаты

и для этой задачи.

Теорема 2.1.2. Жадный алгоритм 15 является (1 − e

−1

приближенным алгоритмом для задачи 11 «К-покрытие».

Доказательство. Пусть Y

обозначает число покрытых эле-

ментов после i-го шага жадного алгоритма, а M — оптимум

в задаче о k-покрытии. Справедливо следующее неравенство

(см. упражнение 2.1.1):

i+1

≥ Y

M − Y

+ Y



1 −



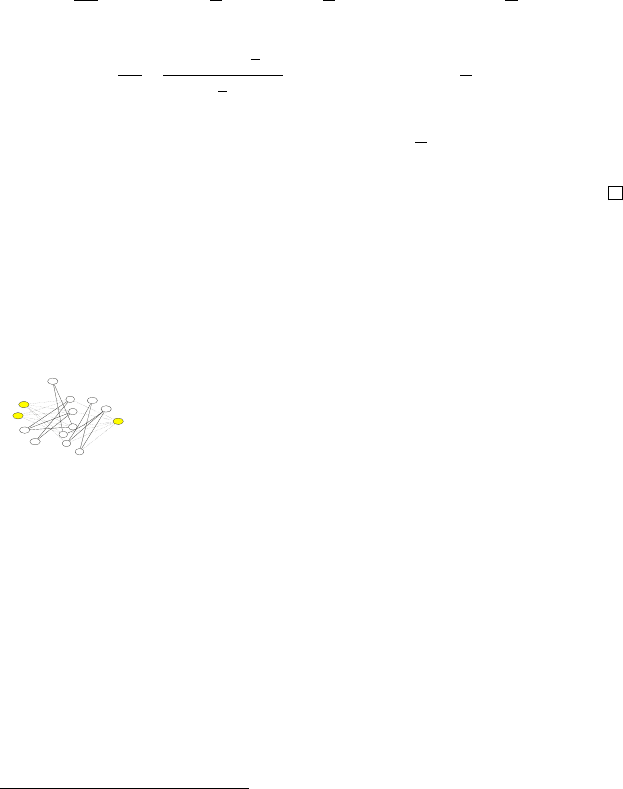
2.1. Алгоритмы с оценками точности 75

Решая это рекуррентное неравенство, получим:

≥

1 +



1 −





1 −



+ . . . +



1 −



k−1

1 −



1 −



= M

1 −



1 −



≥

≥ M



1 − exp



−



= M(1 − e

−1

Упражнение 2.1.4. Покажите, что оценка точности 1 − e

−1

для задачи о k-покрытии асимптотически достижима.

2.1.2. Приближенные алгоритмы для



Вершинного

покрытия



l2_3

l2_2

l2_1

l6_1

l5_1

l4_1

l3_1

l3_2

Жадный и локальный алгоритмы для

вершинного покрытия.

Рассмотрим один из вариантов задачи о покрытии на гра-

фах.

Определение 2.1.2. «Вершинное покрытие»

Для неориентированного графа G = (V, E) подмножество

вершин V

⊆ V называется вершинным покрытием, если

каждое ребро из E содержит хотя бы одну вершину из V

Задача 12. «Минимальное вершинное покрытие»

Дан неориентированный граф G = (V, E) (множество вер-

шин V , множество ребер E). Найти вершинное покрытие ми-

нимальной мощности.

В англоязычной литературе — Vertex Cover.

В англоязычной литературе — Min Vertex Covering.

76 Глава 2. Аппроксимация с гарантированной точностью

Первая интуитивная идея для решения задачи 12 «Min

Vertex Covering» — использовать жадный алгоритм, выбира-

ющий на каждом шаге вершину, имеющую на этом шаге наи-

большее число непокрытых ребер (см. алгоритм 16).

Несмотря на «интуитивную разумность», оказалось, что

этот алгоритм не обеспечивает даже константной точности.

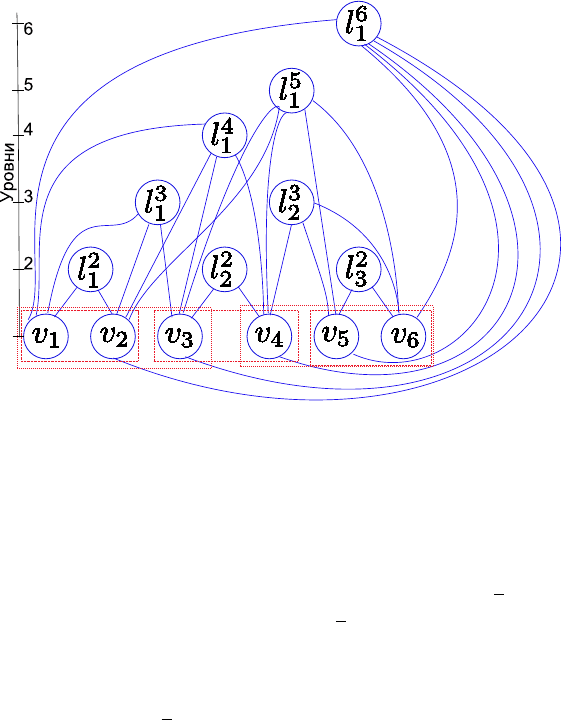
Рис. 2.1. «Плохой» граф для жадного алгоритма вершинного покрытия

Например, «плохим» для этого алгоритма будет граф, об-

разованный следующим образом (см. рис. 2.1):

• Введем n вершин «первого уровня» v

, . . . , v

• Разобьем вершины первого уровня на b

c непересе-

кающихся пар, добавим b

c вершин второго уровня

, . . . , l

bn/2c

, и соединим каждую добавленную верши-

ну со «своей» парой вершин первого уровня.

• Добавим b

c вершин третьего уровня l

, . . . , l

bn/3c

, при-

чем соединим каждую из них со всеми вершинами из од-

2.1. Алгоритмы с оценками точности 77

Алгоритм 16. Жадный алгоритм для вершинного покрытия

def greedyVertexCovering (G):

C ← set ()

while G.number_of_edges () > 0 : # цикл сложности O(|E|)

nodeMaxDegree, maxDegree ← None, None

for n ∈ G.nodes (): # цикл сложности O(|V |)

if ¬maxDegree ∨ G.degree (n) > maxDegree:

nodeMaxDegree ← n

maxDegree ← G.degree (n)

C.add (nodeMaxDegree)

for e ∈ G.edges (nodeMaxDegree):

G.delete_edge (e) # удаляем покрытые ребра

return C

• Закрашенные вершины составляют вершинное покрытие .

• Пунктиром показаны покрытые (удаленные) ребра.

78 Глава 2. Аппроксимация с гарантированной точностью

ной из непересекающихся троек вершин первого уровня

, . . . , v

. . .

• Добавим последнюю (b

n−1

c) вершину n − 1–го уровня,

соединенную с n − 1 вершиной первого уровня.

Для всех вершин уровня k > 1 степень вершины будет ров-

но k, степень вершин первого уровня будет не больше n − 2

(степень n − 2 будет у вершин первого уровня, которые оказа-

лись связанными со всеми вершинами верхних уровней).

И хотя очевидным вершинным покрытием для такого гра-

фа являются вершины v

, . . . , v

, алгоритм 16 начнет «есть»

вершины начиная с верхних уровней, при этом степени вер-

шин v

, . . . , v

будут уменьшаться, так что в вершинное по-

крытие войдут только все вершины l

, и не войдет ни одна

из v

, . . . , v

. Работа алгоритма на таком графе (для n = 6)

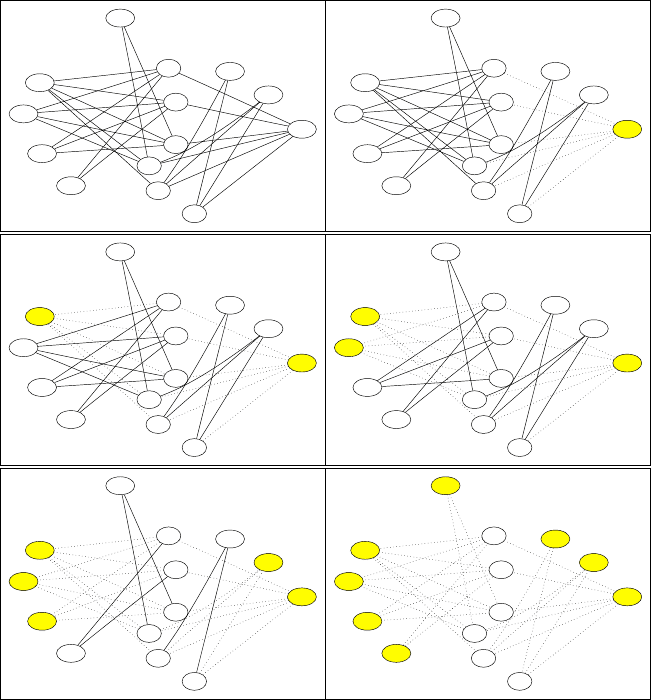
показана на рис. 2.2.

Посчитаем f

число вершин, выбранных алгоритмом 16, и

сравним его с f

∗

— оптимальным размером вершинного покры-

тия для этого графа:

n−1

j=2





n−1

j=2



− 1



= n

n−1

j=2

− (n − 2) >

> n

dx − n = n(ln n − ln 2 − 1) ≥ f

∗

(ln n − ln 2 − 1).

И хотя жадный алгоритм не смог обеспечить никакой кон-

статной точности приближения для задачи 12 «Min Vertex

Covering», оказалось, что есть еще более простой, не «жад-

ный», а скорее «ленивый», локальный алгоритм 17, который

является 2-приближенным. Алгоритм 17 просто добавляет для

первого попавшегося непокрытого ребра обе его вершины, ис-

ключает покрытые этими вершинами ребра, после чего цикл

повторяется.

2.1. Алгоритмы с оценками точности 79

Алгоритм 17. «Ленивый» алгоритм для задачи 12 «Min

Vertex Covering»

def lazyVertexCovering (G):

C ← set ()

while G.number_of_edges () > 0 : # цикл сложности O(|E|)

(u, v) ← G.edges ()[0] # первое попавшееся ребро

C.add (u)

C.add (v)

for e ∈ G.edges (u):

G.delete_edge (e)

for e ∈ G.edges (v):

G.delete_edge (e)

return C

• Закрашенные вершины составляют вершинное покрытие .

• Пунктиром показаны покрытые (удаленные) ребра.

80 Глава 2. Аппроксимация с гарантированной точностью

Рис. 2.2. Неоптимальность жадного алгоритма для вершинного покрытия

l2_3

l2_2

l2_1

l6_1

l5_1

l4_1

l3_1

l3_2

l2_3

l2_2

l2_1

l6_1

l5_1

l4_1

l3_1

l3_2

l2_3

l2_2

l2_1

l6_1

l5_1

l4_1

l3_1

l3_2

l2_3

l2_2

l2_1

l6_1

l5_1

l4_1

l3_1

l3_2

l2_3

l2_2

l2_1

l6_1

l5_1

l4_1

l3_1

l3_2

l2_3

l2_2

l2_1

l6_1

l5_1

l4_1

l3_1

l3_2

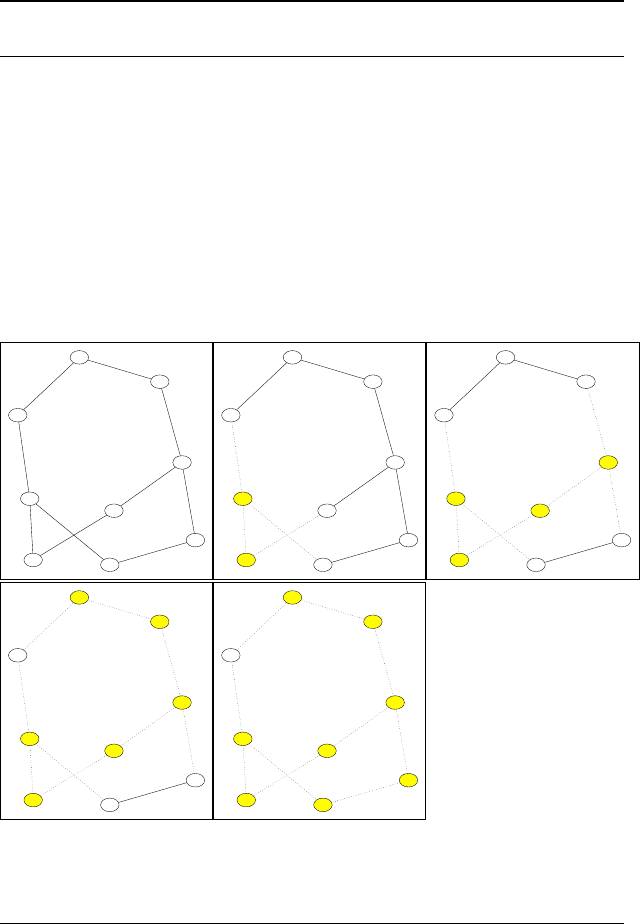
Несмотря на «вопиющую неоптимальность» — добавление

в вершинное покрытие для выбранного ребра обеих вершин,

этот алгоритм может гарантировать константную точность, в

частности, на рис. 2.3 видно, как он выигрывает у жадного

алгоритма на «плохих» для жадного алгоритма графах.

Итак, докажем точность приближения.