Кузюрин Н.Н. Фомин С.А. Эффективные алгоритмы и сложность вычислений

Подождите немного. Документ загружается.

1.1. Примеры задач и алгоритмов 31

Вообще, используя специальные структуры данных (оче-

реди приоритетов на основе фибоначчиевой кучи), можно до-

биться оценки сложности O(n log n+m), где n — число вершин,

а m — число ребер графа.

Упражнение 1.1.2. Приведите пример графа с отрицатель-

ными весами, но без циклов отрицательной длины, для кото-

рого алгоритм Дейкстры даст неправильный ответ.

Упражнение 1.1.3. Неориентированный граф G = (V, E)

представляет телекоммуникационную сеть, причем с каждым

ребром e ∈ E ассоциирована «надежность», 0 ≤ p

≤ 1, т. е.

вероятность успешного прохождения сигнала (в обе стороны)

по ребру e. Считая события успешного или неуспешного про-

хождения сигнала по различным ребрам независимыми, при-

думайте алгоритм нахождения наиболее надежных маршрутов

между данным узлом и всеми остальными.

Для поиска кратчайших путей между любыми двумя

парами вершин можно использовать |V | запусков алгорит-

ма 7 «Дейкстры», что даст эффективное решение этой задачи

алгоритмом со сложностью O(n

). Также алгоритм 7 «Дейкст-

ры» будет работать на ориентированных графах с неотрица-

тельными весами дуг.

Однако такой подход не будет работать на задаче о крат-

чайших путях на ориентированном графе, дуги которого могут

иметь отрицательные веса (с запретом на наличие в графе цик-

лов отрицательной длины, т.к. очевидно, что при их наличии

оптимального решения быть не может).

Задача 6. «Кратчайшие пути с отрицательными расстоя-

ниями».

Задан ориентированный граф G = (V, E) и весовая функция

на дугах w

: e → Z, отображающая ребра в целые числа,

такая, что в графе нет цикла отрицательной длины. Найти

минимальные длины путей между всеми парами вершин.

32 Глава 1. Алгоритмы и их сложность

Алгоритм 8. Алгоритм Флойда-Уоршолла

for k ∈ range (N ): # N — размер матрицы

DD ← array (D) # Сохраняем D

k−1

в DD

for v1 ∈ range (N ):

for v2 ∈ range (N ):

D[v1, v2] ← min (DD[v1, v2], DD[v1, k] + DD[k, v2 ])

Иллюстрация работы показана на рис. 1.3.

Для решения этой задачи применяется алгоритм 8 «Флой-

да–Уоршолла», использующий методы динамического про-

граммирования. В этом алгоритме последовательно выполня-

ются n = |V | итераций, улучшая матрицу D

минимальных

стоимостей пути из вершины i в вершину j, с возможным

использованием (для k-й итерации) промежуточных вершин

из множества 1, . . . , k. Вычислять эту матрицу очень легко,

изначально она определяется весовой функцией дуг, D

= w

для тех i и j, для которых есть дуга (i, j), и +∞ для осталь-

ных. Обновление этой матрицы на k-й итерации происходит по

очевидной формуле:

= min



k−1

, D

k−1

+ D

k−1



где D

k−1

— значение этой матрицы на предыдущей итерации.

Таким образом, очевидна и корректность (то, что алгоритм на-

ходит требуемое решение) алгоритма 8 «Флойда–Уоршолла»,

и оценка его сложности O(n

). В иллюстрации работы алго-

ритма 8 «Флойда–Уоршолла» приведен вывод промежуточных

структур и изображен входной граф.

Таким образом, использование «жадных алгоритмов»

и «динамического программирования», позволили постро-

ить эффективные алгоритмы для задач, очевидным решением

которых был полный перебор, требующий экспоненциального

времени. Об этих алгоритмах и понятии эффективности будет

более подробно рассказано в следующих разделах.

1.1. Примеры задач и алгоритмов 33

Рис. 1.3. Иллюстрация работы алгоритма 8 «Флойда–Уоршолла»

NY(0)

Kiev(4)

$80

Moscow(1)

$60

Minsk(2)

$-5

Berlin(3)

$50

$10

$50

$30

$20

$30

$15

k=0 (NY) NY Moscow Minsk Berlin Kiev

NY 0 ∞ ∞ ∞ 80

Moscow 60 0 -5 50 10

Minsk ∞ 10 0 ∞ ∞

Berlin 50 30 20 0 30

Kiev ∞ 15 15 ∞ 0

k=1

(Moscow)

NY Moscow Minsk Berlin Kiev

NY 0 ∞ ∞ ∞ 80

Moscow 60 0 -5 50 10

Minsk ∞⇒70 10 0 ∞⇒60 ∞⇒20

Berlin 50 30 20 0 30

Kiev ∞⇒75 15 15⇒10 ∞⇒65 0

k=2 (Minsk) NY Moscow Minsk Berlin Kiev

NY 0 ∞ ∞ ∞ 80

Moscow 60 0 -5 50 10

Minsk 70 10 0 60 20

Berlin 50 30 20 0 30

Kiev 75 15 10 65 0

k=3 (Berlin) NY Moscow Minsk Berlin Kiev

NY 0 ∞ ∞ ∞ 80

Moscow 60 0 -5 50 10

Minsk 70 10 0 60 20

Berlin 50 30 20 0 30

Kiev 75 15 10 65 0

k=4 (Kiev) NY Moscow Minsk Berlin Kiev

NY 0 ∞⇒95 ∞⇒90 ∞⇒145 80

Moscow 60 0 -5 50 10

Minsk 70 10 0 60 20

Berlin 50 30 20 0 30

Kiev 75 15 10 65 0

34 Глава 1. Алгоритмы и их сложность

Задача 4 «TSP» и задачи о кратчайших путях чрезвычайно

похожи по своей структуре, и мы постарались подчеркнуть это

сходство в их формулировках.

Таким образом, сравнительно успешно устранив перебор

для задач о кратчайших путях, естественно задаться анало-

гичным вопросом для задачи 4 «TSP». Довольно быстро вы-

ясняется, впрочем, что ни один из «естественных» методов со-

кращения перебора к последней задаче неприменим. Таким об-

разом, встает законный вопрос: а можно ли вообще решить

задачу 4 «TSP» с помощью точного алгоритма, существенно

более эффективного, нежели переборный?

Одним из главных достижений теории сложности вычисле-

ний является теория N P-полноты, позволяющая в 99% случа-

ев дать вполне удовлетворительный ответ на этот вопрос.

Эта теория будет рассмотрена далее в разделе 6.2, пока же

термин N P-полная задача (или N P-трудная задача) можно

понимать неформально в смысле труднорешаемая переборная

задача, для которой существование алгоритма, намного бо-

лее эффективного, нежели простой перебор вариантов, крайне

маловероятно.

В частности, в одном из первых исследований было пока-

зано, что задача 4 «TSP» N P-трудна, и, тем самым, на воз-

можность построения для нее точного эффективного алгорит-

ма рассчитывать не приходится.

Поэтому следующий вопрос, на который пытается отве-

тить теория сложности вычислений: какие рекомендации мож-

но дать практическому разработчику алгоритмов в такой ситу-

ации, т. е. в тех случаях, когда результаты диагностики инте-

ресующей его задачи на существование для нее точных эффек-

тивных алгоритмов столь же неутешительны, как и в случае

задачи 4 «TSP»?

Одна из таких рекомендаций состоит в следующем: попы-

таться проанализировать постановку задачи и понять, нельзя

ли видоизменить ее формулировку так, чтобы, с одной сторо-

1.1. Примеры задач и алгоритмов 35

ны, новая формулировка все еще была бы приемлема с точки

зрения практических приложений, а с другой стороны, чтобы

в этой формулировке задача уже допускала эффективный ал-

горитм. Кстати, в качестве побочного продукта в ряде случаев

такой сложностной анализ позволяет лучше понять природу

задачи уже безотносительно к ее вычислительной сложности.

Например, пусть некий начинающий проектировщик сетей

задумал спроектировать оптимальную компьютерную сеть, со-

единяющую n корпусов общежитий. Он только что изучил

кольцевые топологии сети и вознамерился проложить кольце-

вой сетевой маршрут через все корпуса общежитий. Стоимость

прокладки кабеля между любыми двумя корпусами известна

(если между какими-то корпусами кабель проложить нельзя,

например, из-за постоянных работ по ремонту теплотрасс, то

стоимость полагается равной +∞). Формулировка этой зада-

чи в чистом виде совпадает с задачей 4 «TSP». Как мы уже

видели раньше, если число корпусов больше 10, то проектиров-

щику потребуется доступ к дорогой вычислительной технике,

если еще увеличить размер задачи, то можно не получить оп-

тимальное решение за время человеческой жизни.

Что же делать начинающему проектировщику сети?

Почитав дальше книгу по проектированию сетей, он решает

построить минимальную связную сеть, используя минималь-

ные связные (из n − 1 дуги) подграфы исходного потенциаль-

ного графа связности общежитий, так называемые остовные

деревья

Задача 7. «Минимальное остовное дерево» (Minimum Span-

ning Tree)

Задан связный неориентированный граф G = (V, E),

где V = {v

, . . . , v

}—множество вершин, |V | = n, E—

множество ребер между ними, и весовая функция w : E → Z+

В англоязычной литературе — spanning trees.

Можно вводить положительные целые веса на ребрах, как

≡ w(v

, v

36 Глава 1. Алгоритмы и их сложность

Требуется найти наименьший возможный вес остовного

дерева, т. е.

min

(i,j)∈T

w(v

, v

), (1.2)

где минимум берется по всем остовным деревьям на n вер-

шинах (по всем множествам T из (n − 1) дуг, связывающим

все n вершин в единую сеть).

На первый взгляд, переход от задачи 4 «TSP» к зада-

че 7 «Minimum Spanning Tree» только увеличивает трудности,

стоящие перед нашим проектировщиком: перебор по множе-

ству всех замкнутых путей заменяется перебором по еще более

«необозримому» множеству произвольных остовных деревьев.

Тем не менее, эта интуиция в данном случае в корне ошибоч-

на, поскольку так же, как и в случае с кратчайшими путями,

существуют эффективные алгоритмы для задачи 7 «Minimum

Spanning Tree».

Опишем один из них, так называемый алгоритм Прима

В этом алгоритме минимальный остов строится постепенно:

сначала выбирается произвольная вершина, которая включает-

ся в остов, затем на каждой итерации к текущему остову добав-

ляется наиболее дешевое ребро (u, v), соединяющее какую-либо

вершину из остова u с какой-либо вершиной v не из остова.

Алгоритм Прима и иллюстрация его работы представлены

как алгоритм 9 «MST Прима». Видно, что этот алгоритм по-

хож на алгоритм 7 «Дейкстры».

Упражнение 1.1.4. Для алгоритма 9 «MST Прима» дока-

жите корректность, т. е., что алгоритм действительно находит

оптимальное решение.

Видно, что сложность алгоритма 9 «MST Прима», гаран-

тирующего оптимальное решение, равна O(n

), а не экспонен-

циальна, как в алгоритме для задачи 4 «TSP».

Впервые опубликован в [Pri57]. Для этой задачи широко известен так-

же алгоритм Краскала [99a].

1.1. Примеры задач и алгоритмов 37

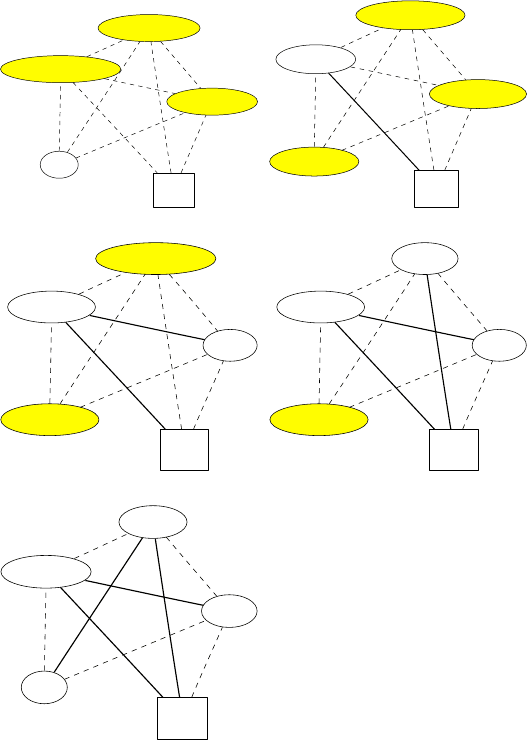
Рис. 1.4. Иллюстрация работы алгоритма 9 «MST Прима»

Moscow ($15)

$60

Berlin ($20)

$50

Kiev ($15)

$80

Minsk

Start

$15

$50

$10

$20

$15

$30

NY ($60)

Moscow

$60

Berlin ($20)

$50

Kiev ($10)

$80

Minsk

Start

$15

$50

$10

$20

$15

$30

NY ($60)

Moscow

$60

Berlin ($20)

$50

Kiev

$80

Minsk

Start

$15

$50

$10

$20

$15

$30

NY ($50)

Moscow

$60

Berlin

$50

Kiev

$80

Minsk

Start

$15

$50

$10

$20

$15

$30

Moscow

$60

Berlin

$50

Kiev

$80

Minsk

Start

$15

$50

$10

$20

$15

$30

Ребра из минимального остовного дерева выделяются

жирным.

38 Глава 1. Алгоритмы и их сложность

Алгоритм 9. Алгоритм Прима

def MST_Prim (G, s):

MST ← {} # мин. остовное дерево, хэш (узел:

узел-предшественник)

ToVisit ← {s : 0} # узлы граничащие с MST, хеш (узел: стоимость)

Predecessor ← {s: s} # хэш: вершины из которых включают другие

while ToVisit : # пока есть непосещенные вершины

v ← argmin (ToVisit) # ближайшая достижимая вершина

MST[v] ← Predecessor[v]; # запоминаем, откуда пришли

del ToVisit[v]; del Predecessor[v]; # больше не посещать

for w ∈ G.neighbors (v): # для всех соседей вершины v

if w 6∈ MST : # которые еще не в MST

обновляем стоимость включения в MST

if w 6∈ ToVisit ∨ G.get_edge (v, w) < ToVisit[w]:

ToVisit[w] ← G.get_edge (v, w) # кандидат

Predecessor[w] ← v

return MST

Иллюстрация работы показана на рис. 1.4.

Упражнение 1.1.5. Докажите, что жадный алгоритм в зада-

че 4 «TSP», т. е. алгоритм стартующий с некоторой вершины и

пытающийся добавлять наиболее дешевые ребра к еще непосе-

щенным вершинам, не гарантирует нахождение оптимального

решения.

Этот поучительный пример еще раз наглядно демонстриру-

ет, что при устранении перебора внутренняя структура задачи

имеет гораздо большее значение, нежели размер полного пе-

ребора вариантов, а внешность задачи во многих случаях бы-

вает крайне обманчивой, и никакие правдоподобные рассуж-

дения «по аналогии» не могут заменить настоящего сложност-

ного анализа. Последний в ряде случаев приводит к довольно

неожиданным выводам, зачастую противоречащим обыкновен-

1.1. Примеры задач и алгоритмов 39

ной интуиции.

Перечислим основные выводы из вышеизложенного:

1) Для подавляющего большинства задач дискретной опти-

мизации существуют тривиальные алгоритмы решения,

основанные на переборе всех вариантов

. Переборные

алгоритмы становятся нереализуемыми с практической

точки зрения уже при сравнительно небольшом размере

входных данных (см. таблицу 1.1).

2) Теория сложности вычислений занимается изучением

возможности построения и анализом эффективных алго-

ритмов — в данном случае алгоритмов, в которых перебор

вариантов устранен или, по крайней мере, сокращен до

приемлемого уровня.

3) Основное внимание концентрируется на сравнительно

небольшом числе «модельных», классических алгорит-

мических задач, каждая из которых описывает огромное

число самых разнообразных приложений.

4) Наиболее предпочтительным решением является постро-

ение точного эффективного алгоритма для рассматрива-

емой задачи.

5) Имеется обширный класс N P-полных задач, для которых

существование точного эффективного алгоритма пред-

ставляется крайне маловероятным. Классификация пе-

реборных задач на N P-полные и те, которые поддаются

решению с помощью точного эффективного алгоритма,

оказывается весьма успешной — под нее подпадает по-

давляющее большинство переборных задач.

6) В тех случаях, когда интересующая разработчика прак-

тических алгоритмов задача оказывается N P-полной,

Пример задач, которых невозможно решить даже конечным перебо-

ром — задачи выполнимости целочисленных нелинейных неравенств.

40 Глава 1. Алгоритмы и их сложность

имеет смысл попробовать построить эффективный ал-

горитм для какой-либо ее модификации (т. е. близкой

модельной задачи) либо частного случая, приемлемых

с практической точки зрения.

7) В тех случаях, когда такую модификацию найти не уда-

ется, имеет смысл попробовать построить для решения

задачи приближенный эффективный алгоритм, который

гарантирует нахождение решения, отличающегося от оп-

тимального не более чем в заданное число раз.

1.1.3. Приближенные алгоритмы:



Составление

расписаний



Очень часто алгоритмы, используемые на практике, не находят

точное решение, а довольствуются нахождением приближенно-

го (в некотором смысле) решения. Такие алгоритмы называют-

ся приближенными. Особенно часто приближенные алгоритмы

применяют для решения N P-трудных задач, причем актуаль-

ной задачей является анализ точности получаемого решения.

Рассмотрим для иллюстрации одну из простейших задач

составления расписаний.

Задача 8. «Составление расписаний»

Имеется m одинаковых машин и n независимых работ

с длительностями исполнения t

, . . . , t

. Распределить эти

работы по машинам так, чтобы минимизировать макси-

мальную загрузку (загрузка машины равна сумме длительно-

стей работ, приписанных данной машине).

Несмотря на простоту постановки, эта задача трудна с вы-

числительной точки зрения (N P-трудна). Даже для случая

m = 2 она остается N P-трудной, поскольку к ней сводится

N P-трудная задача о камнях: для заданного множества из n

камней с весами t

, . . . , t

выяснить, можно ли разбить это