Кузнецов А.П. Программа-минимум по нелинейной динамике

Подождите немного. Документ загружается.

Неподвижных точек две, как и у логистического отображения. Они существуют

при условии:

(

)

−>

Найдем теперь 2-цикл:











−−=

byxx

Подставляя второе уравнение в третье и четвертое в первое, получаем

bxxx

−−=

или

(

)

()

xxb

−=+

Складывая и вычитая эти уравнения, получим

()( )

(

)

[

]

()()()()

[]

221

211212

2121

xxxxxxb

+−=−+

−+−=++

Если

, то из второго уравнения следует, что

xx ≠

а тогда из первого –

(

)

−+

xx .

По теореме Виета элементы 2-цикла ищем из квадратного уравнения

(

)

−+

−

Откуда

()

2,1

x +−±

λλ

Таким образом, 2-цикл возможен при условии:

()

b+>

При b=0 получаем λ=3/4=0,75 – значение, при котором неподвижная точка те-

ряет устойчивость и рождается 2-цикл. Естественно предположить, что анало-

гичная ситуация имеет место и в отображении Эно, хотя доказать это значи-

тельно сложнее. Мы этого делать не будем, а используем компьютерное моде-

лирование.

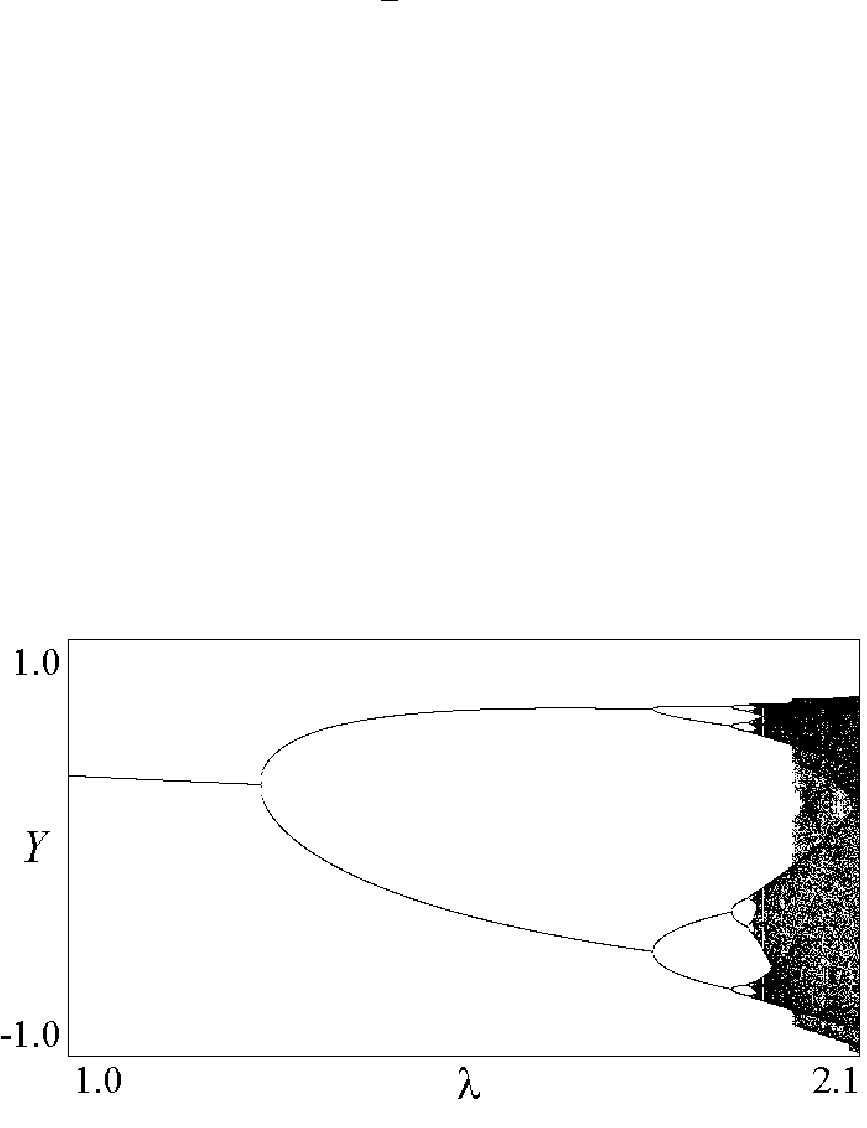
На следующем рисунке показано бифуркационное дерево отображения

Эно при b=0,3. Можно видеть, что оно не только демонстрирует рождение ус-

тойчивого 2-цикла из неподвижной точки, но и весь каскад бифуркаций удвое-

ния периода, хаос и окна непериодичности в хаосе. Новым является то, что де-

рево иногда скачком “разбухает”. Такое явление в нелинейной динамике назы

вают кризисом.

Рис.3

Надо сказать, что мы описали лишь простейшие свойства отображения

Эно. На самом деле его динамика столь многообразна, что ему можно посвя-

тить целую монографию. Более того, многие современные исследователи по-

прежнему используют отображения Эно в своих работах.

Задачи.

1. Нарисуйте на плоскости b, λ область существования устойчивой неподвиж-

ной точки. Параметр –1<b<1.

2. Создайте программу, рисующую бифуркационное дерево для отображения

Эно. Постройте его для случаев b=0,3, b=0,6, b=0,9. Что происходит с дере-

вом при приближении b к единице?

ФАЗОВОЕ ПРОСТРАНСТВО И АТТРАКТОРЫ

Как проследить за эволюцией динамической системы при заданных на-

чальных условиях? Для этого нужно "увидеть", что происходит с задающими

динамическую систему переменными x, y,... в по мере эволюции во времени.

Введем некоторое пространство, по осям координат которого отложим эти пе-

ременные. Подобное пространство принято называть фазовым. Фраза "задано

начальное состояние динамической системы", теперь означает, что задана точка

в фазовом пространстве. "Включим" время. Если система определена дискрет-

ным отображением, например, отображением Эно или прыгающего шарика, то

изображающая точка при каждой итерации будет совершать "прыжки" в фазо-

вом пространстве.

Динамическая система полностью задает закон эволюции во времени, од-

нако, чтобы получить полную информацию о характере такой эволюции надо

провести исследование для различных начальных условий. Современные ком-

пьютеры делают эту задачу не умозрительной, а вполне реальной и позволяют

получать наглядные геометрические образы такого процесса.

Итак, рассмотрим множество начальных состояний системы. В фазовом

пространстве в этом случае будем иметь уже не одну изображающую точку, а

целое облако. При "включении" времени они все двинутся по своим траектори-

ям (в случае дифференциальных уравнений), либо начнут совершать "прыжки"

(в случае дискретных отображений). При компьютерном моделировании ра-

зумно создать мгновенные "снимки" облака через определенные промежутки

времени (число итераций). Тогда можно следить за эволюцией облака на экране

дисплея.

Перейдем к компьютерному моделированию. В качестве исследуемой

системы выберем отображение Эно.

nnn

byxx

−

Здесь λ и b – параметры. На рис.1 показаны мгновенные "снимки" облака изо-

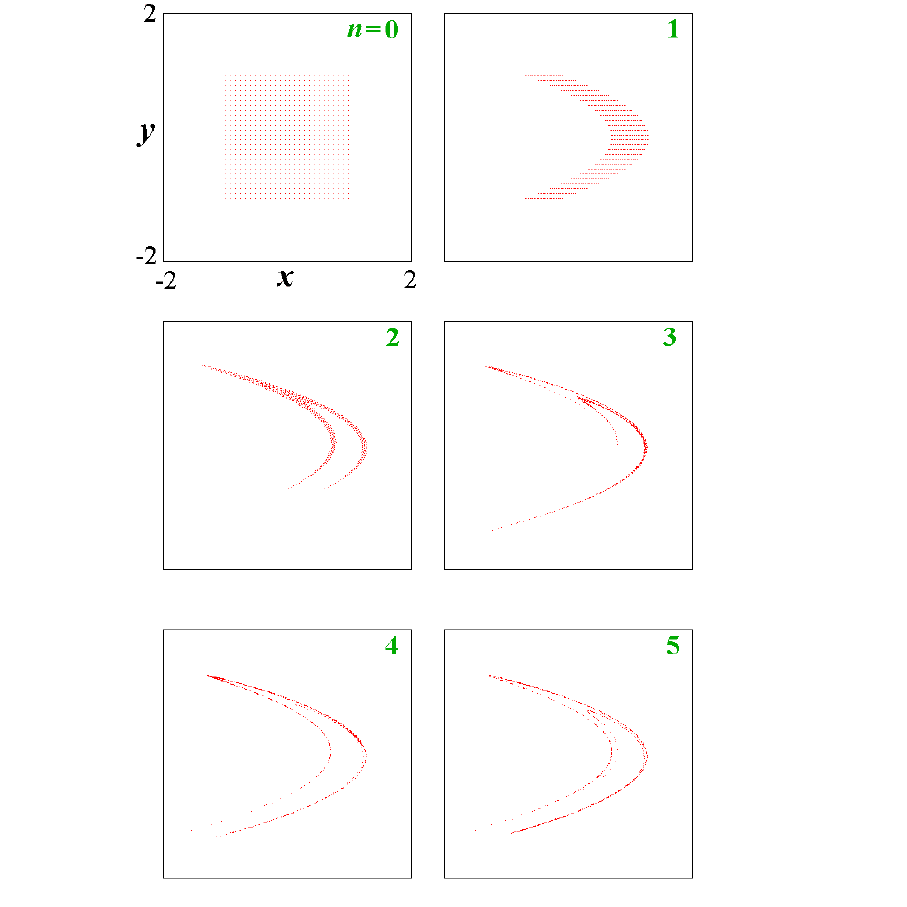
бражающих точек на фазовой плоскости для отображения Эно, сделанные через

одну итерацию.

Рис.1

Заметим, что при работе за компьютером весьма удобно и увлекательно наблю-

дать эволюцию облака изображающих точек в режиме "компьютерной мульти-

пликации".

Наиболее существенный результат, который вытекает из компьютерного

моделирования (рис.1), состоит в том, что облако изображающих точек "кон-

денсируется" на некоторые предельные объекты. Их называют аттракторами

(от английского to attract – притягивать). Динамические системы, которые об-

ладают аттракторами, называют диссипативными.

Существование аттракторов приводит к весьма важным выводам о поведе-

нии системы. В этом случае исследование установившихся режимов, т.е. режи-

мов, которые наблюдаются по истечении достаточно большого времени, экви-

валентно изучению геометрической структуры аттрактора. (Соответствующий

подход в теории колебаний был высказан А.А.Андроновым и лежит в основе

понятий об автоколебаниях. За примерами автоколебательных систем в реаль-

ной жизни далеко ходить не надо, например, часы – это автоколебательная сис-

тема.)

Процесс "конденсации" изображающих точек на аттрактор занимает неко-

торое время. Как видно из рис.1 в результате изображающие точки притягива-

ются к некоторой сложной слоистой структуре. Если просмотреть с помощью

компьютера как "микроскопа" отдельные фрагменты такого аттрактора, то об-

наруживается, что он весь состоит из отдельных "нитей" и областей пустого

пространства, причем каждая нить в свою очередь имеет аналогичную тонкую

структуру. Как говорят, аттрактор в этом случае обладает фрактальными свой-

ствами. Подобные аттракторы были обнаружены в семидесятые годы нашего

века и получили название странных. А колебательные режимы, которым не от-

вечает определенный период, назвали динамическим хаосом. Обнаружение ди-

намического хаоса явилось своего рода революцией в науке, так как оказалось,

что простые предсказуемые системы могут демонстрировать в установившимся

режиме нерегулярную непериодическую динамику.

Итак, если исследуемая система диссипативна, то можно изучать лишь ее

аттракторы. Это упрощает компьютерное моделирование - не надо следить за

всеми изображающими точками. Достаточно выбрать одну из них, выполнить

определенное (не очень маленькое) число итераций, чтобы эта точка "вышла"

на аттрактор, а затем вывести ее движение на экран компьютера. Тогда мы и

получим портрет аттрактора.

Задачи.

1. Напишите программу, которая реализует конденсацию изображающих то-

чек на аттрактор Эно.

2. Напишите программу, которая строит на экране аттрактор отображения

Эно. (Для этого наеобходимо предварительно выполнить несколько сот

итерация без вывода на экран для выхода ихзображающей точки на ат-

трактор.

3. Найдите примеры значений параметров, которые отвечают устойчивой

неподвижной точке, циклу периода 2, циклу периода 4.

4. Создайте программу, которая позволяет просматривать фрагменты ат-

трактора с некоторым увеличением. (Можно, например, с помощью мыши

выделять фрагмент аттрактора.) С ее помощью убедитесь, что аттрактор

Эно обладает фрактальной структурой.

5. Постройте на плоскости двух переменных аттрактор, отвечающий пре-

дельному переходу от отображения Эно к логистическому отображению.

Выберите значения параметров, отвечающих как периодическим, так и

хаотическим режимам.

6. Пронаблюдайте конденсацию изображающих точек на аттрактор для ото-

бражения прыгающего шарика.

7. Постройте примеры аттракторов для отображения прыгающего шарика.

Постарайтесь, чтобы Ваша коллекция была достаточно полной.

КАРТЫ ДИНАМИЧЕСКИХ РЕЖИМОВ

Иллюстрации в виде бифуркационных деревьев демонстрируют возмож-

ность нетривиальной эволюции аттракторов и, соответственно, колебательных

режимов динамических систем при вариации одного параметра. Еще более

удивительное разнообразие режимов можно наблюдать, если система характе-

ризуется двумя параметрами. На первый взгляд кажется, что исследование та-

кой системы требует кропотливой работы, и это действительно так. Однако,

сейчас в нелинейной динамике стал популярным весьма простой, наглядный и

информативный прием, который позволяет быстро получать существенную

информацию о системе. Продемонстрируем его на примере кубического ото-

бражения

(1) x=a-bx+x

n+1 n n

Компьютерная "технология" двухпараметрического исследования состо-

ит в следующем. Выбираются какие-либо значения параметров a и b. Затем вы-

полняется несколько сотен итераций отображения, для того, чтобы система

вышла на аттрактор, а затем - еще несколько сотен итераций уже непосредст-

венно на аттракторе. По мере итераций на аттракторе производится сравнение

начального значения со всеми последующими. Если они совпадают с высокой

(наперед заданной) точностью, то число итераций принимается за период дви-

жения. На плоскости параметров (на экране дисплея) точка отмечается некото-

рым цветом, причем цветовая палитра выбрана заранее, так что движениям с

определенными периодами отвечают определенные цвета. После этого проце-

дура повторяется при слегка измененных значениях параметров, так что в ко-

нечном итоге выполняется полное "сканирование" плоскости параметров. В ре-

зультате плоскость оказывается окрашенной в разные цвета в соответствии с

периодом движения на аттракторе. Области хаоса (непериодические режимы)

также обозначаются специальным образом. По аналогии с географией такую

"раскрашенную" плоскость называют картой динамических режимов.

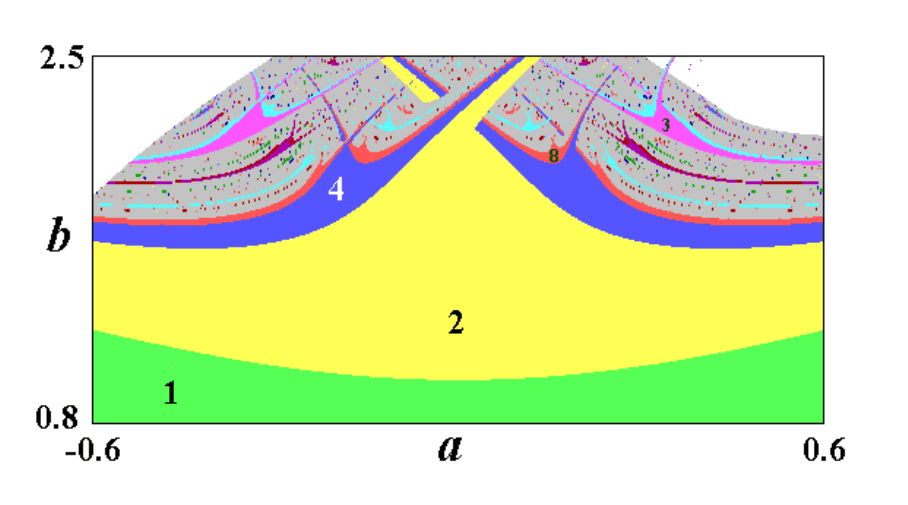
На рис.1 показана карта динамических режимов кубического отображения (1).

Рис.1

Как видим, столь простая модель демонстрирует очень большое разнооб-

разие режимов и бифуркаций. В нижней части рисунка видна граница между

областями устойчивости неподвижной точки и цикла периода 2, представляю-

щая собой линию бифуркации удвоения периода. Линий рождения 4-цикла в

результате аналогичной бифуркации уже две, причем область устойчивости 2-

цикла имеет характерный вид с уходящим "вверх" пересекающимися "отрост-

ками". Таким образом, область устойчивости 2-цикла ограничена этими линия-

ми удвоений, а также двумя линиями складок (термин теории катастроф), обра-

зующими нижнюю границу "отростков". Отметим, что линии складок продол-

жаются внутрь области устойчивости 2-цикла и сходятся в точке, которую в

теории катастроф называют точкой сборки (a=0, b=2), которая, однако, на ри-

сунке не видна. Описанная совокупность бифуркационных линий демонстриру-

ет весьма типичную структуру на картах, названную французским специали-

стом в области нелинейной динамики К.Мира "crossroad area" – "перепутье". На

карте можно видеть две аналогичные конфигурации на базе 8-циклов. Самые

широкие окна устойчивости реализуются на основе 3-циклов, внутри них мож-

но идентифицировать конфигурации "crossroad area", отвечающие областям ус-

тойчивости 6-циклов и т. д.

Правда, карты динамических режимов обладают одним недостатком. Ес-

ли провести сканирование карты различными способами (например снизу

вверх, или слева направо), то отдельные фрагменты карт получаются отличаю-

щимися. Это связано со свойством мультистабильности динамических систем.

Оно состоит в том, что при заданных значениях параметров могут сосущество-

вать одновременно несколько (иногда мало, иногда много) аттракторов. Соот-

ветственно, в зависимости от начальных условий траектория может выйти на

тот или иной аттрактор. Поэтому, построив карту, полезно попробовать сделать

тоже самое, но при других начальных условиях. Полезным также является

прием, когда, сделав маленький шаг по параметру, в качестве начальной в фа-

зовом пространстве берут точку аттрактора, получившегося на предыдущем

шаге. Иногда об этом способе говоря, что карту строят с наследованием началь-

ных условий.

Интересно, что карты режимов можно строить не только для отображе-

ний, но и для дифференциальных систем, если использовать метод сечений Пу-

анкаре. Суть метода состоит в том, что в фазовом пространстве выбирается не-

которая поверхность. После этого мы следим не за всей фазовой траекторией

дифференциальной системы, а лишь за точками ее пересечения с этой поверх-

ностью. Таким образом, мы приходим к дискретному отображению, которые

исследовать уже умеем. Удивительно то, что карты режимов дифференциаль-

ных систем оказываются очень похожими на карты отображений и содержат

элементы, совершенно аналогичные показанным на рис. 1.

В современной нелинейной динамике достаточно много существенных

для теории (иногда говорят эталонных) динамических систем. Среди них и уже

знакомое Вам отображение Эно. Набор карт для них образует своеобразный ат-

лас, с некоторыми «страничками» этого атласа можно познакомиться здесь