Курсовой проект - Основы теории надежности (вариант 22)
Подождите немного. Документ загружается.

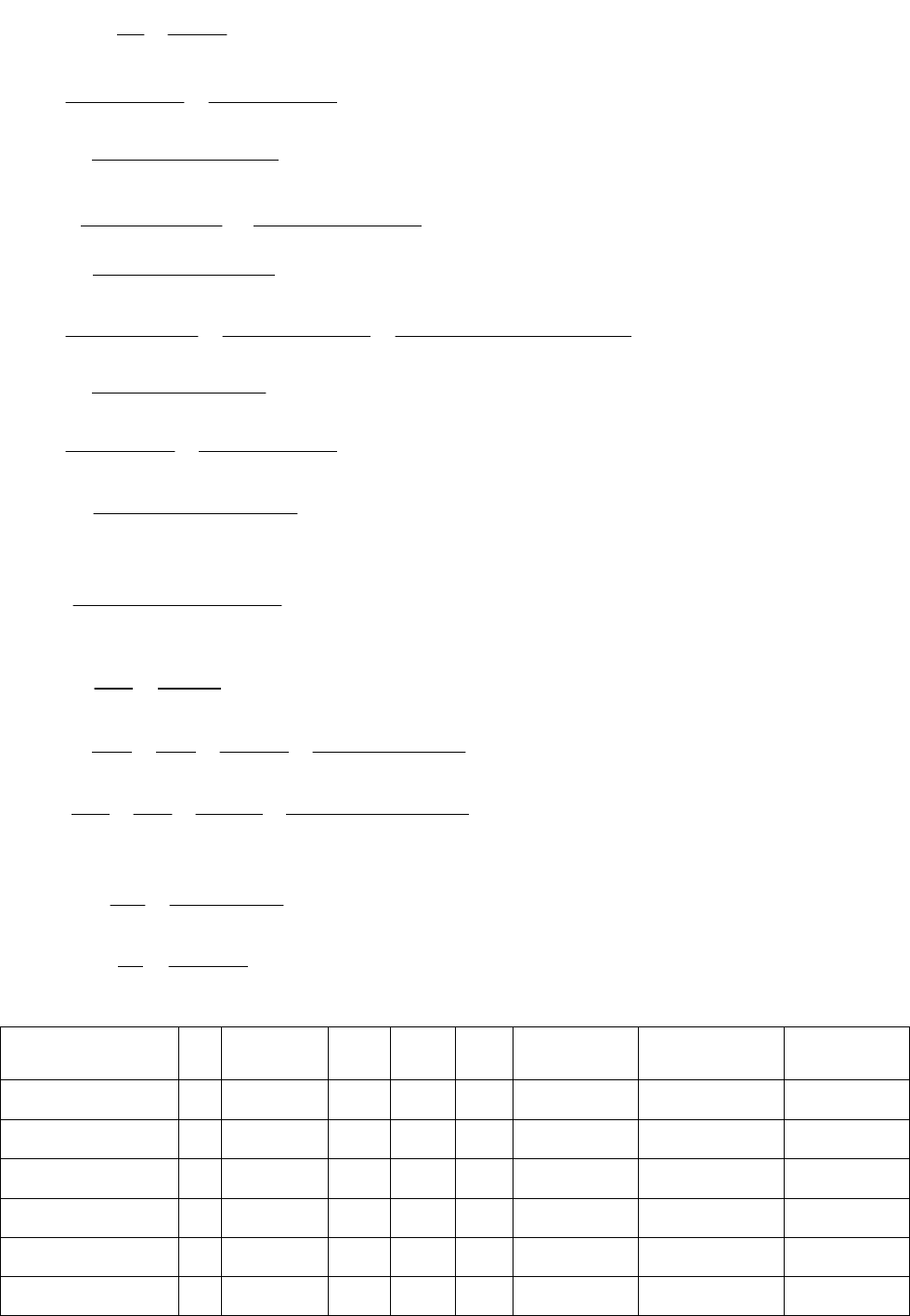
1)
д
2
R
д
ф
R9R1,
н
P
RI
P
Р
К
А
3
3
VT1вх
R1
1095,0
1010
5,00,910
R1
UU
I
0361,0
0,25
1010)10(0,95
К
32-3
R9R1,
н
А
3
3
VT1п
R8
106,1
10)1,5(1,5
0,501
R2R5
UU
I
026,0
0,5
101,5)10(1,6
К
32-3
R8R2,
н
А
3
3
33
VT1R4VT1R6
R3
1031,3
103
5,01012010087,0
R3
UR6I
R3
UU
I
066,0
0,5
103)10(3,31
К
32-3
R7R3,
н
А
3
3
VT1п
R4
10087,0
10120)(1,5
5,001
R6R4
UU
I
3
32-3
R5R4,
н
10045,0
0,25
105,1)10(0,087
К
А
3
R4R6
10087,0II
3
32-3
R6
н
1091,0
1
10120)10(0,087
К
45,0
20
109,0
U
U
К
д
вх
С5С1,
н
41,0
20
101,5106,1
U
R2I
U
U
U
U
К
33
д
R2
д
R2
д
С2
С4С2,
н
52,0
20
1012010087,0
U
R6I
U
U
U
U
К
33
д
R6
д
R6
д
С3
С3
н
3
-3
н
ф
VT2VT1,
н
1025,0
0,2
100,10,5
W
W
К
5
3
3
д
ф
VD2VD1,
н
1033,4
1030
103,1
I
I
К
Тип элемента N
i
6
0
10
,
1/ч
К
н
Ct
o
1
6
10)(
,
1/ч
6
i
10)(N
,
1/ч
6
0i
10N
,
1/ч
R1, R9 – МЛТ – 0,25
– 10кОм
2
0,4 ≈0,1 40
0,27 0,108 0,216 0,8
R2, R8 – МЛТ – 0,5
– 5,1кОм
2 0,5
≈0,1 40
0,27 0,135 0,27 1
R3, R7 – МЛТ – 0,5
– 3,0кОм
2 0,5
≈0,1 40
0,27 0,135 0,27 1
R4, R5 – МЛТ – 0,25
– 1,5кОм
2 0,4
≈0,1 40
0,27 0,108 0,216 0,8
R6 – МЛТ – 1 –
120кОм
1 1,0
≈0,1 40
0,27 0,27 0,27 1
VT1, VT2 – МП42А
2
4,6 ≈0,1 40
0,25 1,15 2,3 9,2
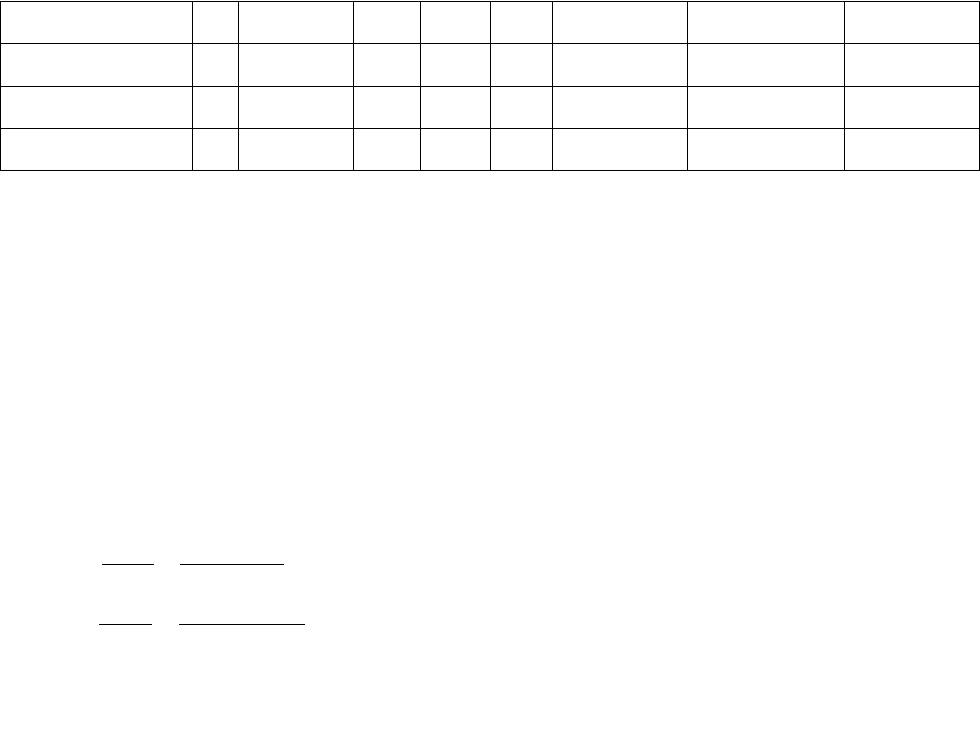
С1, С5 – МБМ –
1000пф
2 2,0 ≈0,5 40 0,54 1,08 2,16 4
С2, С4 – КМ –
300пф
2 1,4 ≈0,4 40 0,9 1,26 2,52 2,8
С3 – К50 – 6 –
0,1мкф
1 2,4 ≈0,6 40 1,24 2,98 2,98 2,4
VD1, VD2 – Д9А 2 0,7 ≈0,1 40 0,15 0,105 0,21 1,4
2)
6
k
1i
i0
104,24N)(
1/ч
Суммарная интенсивность отказов триггера:
6
k
1i
i
10412,11N)()(
i
1/ч
3) Вероятность безотказной работы за 10000 часов:
783,0eeP(10000)
46
10104,24t)(
892,0eeP(10000)
46
1010412,11t)(
4) Среднее время наработки до первого отказа триггера:
40984
104,24
1
)(
1
)(T
6
0
ч
1,87627
10412,11
1
)(
1
)(T
6
0
ч
Основная интенсивность отказов приходится на транзисторы и
конденсаторы (
3,0)(N
i
). Для повышения надежности транзисторов
можно их заменить на кремниевые, а также использовать транзисторы с
радиаторами. Конденсаторы выбирать более надежные. Также значительно
повысить надежность триггера использование облегченных режимов работы
элементов и щадящих условий эксплуатации.
3. Расчет надежности невосстанавливаемых резервируемых систем.
Задача 3.1
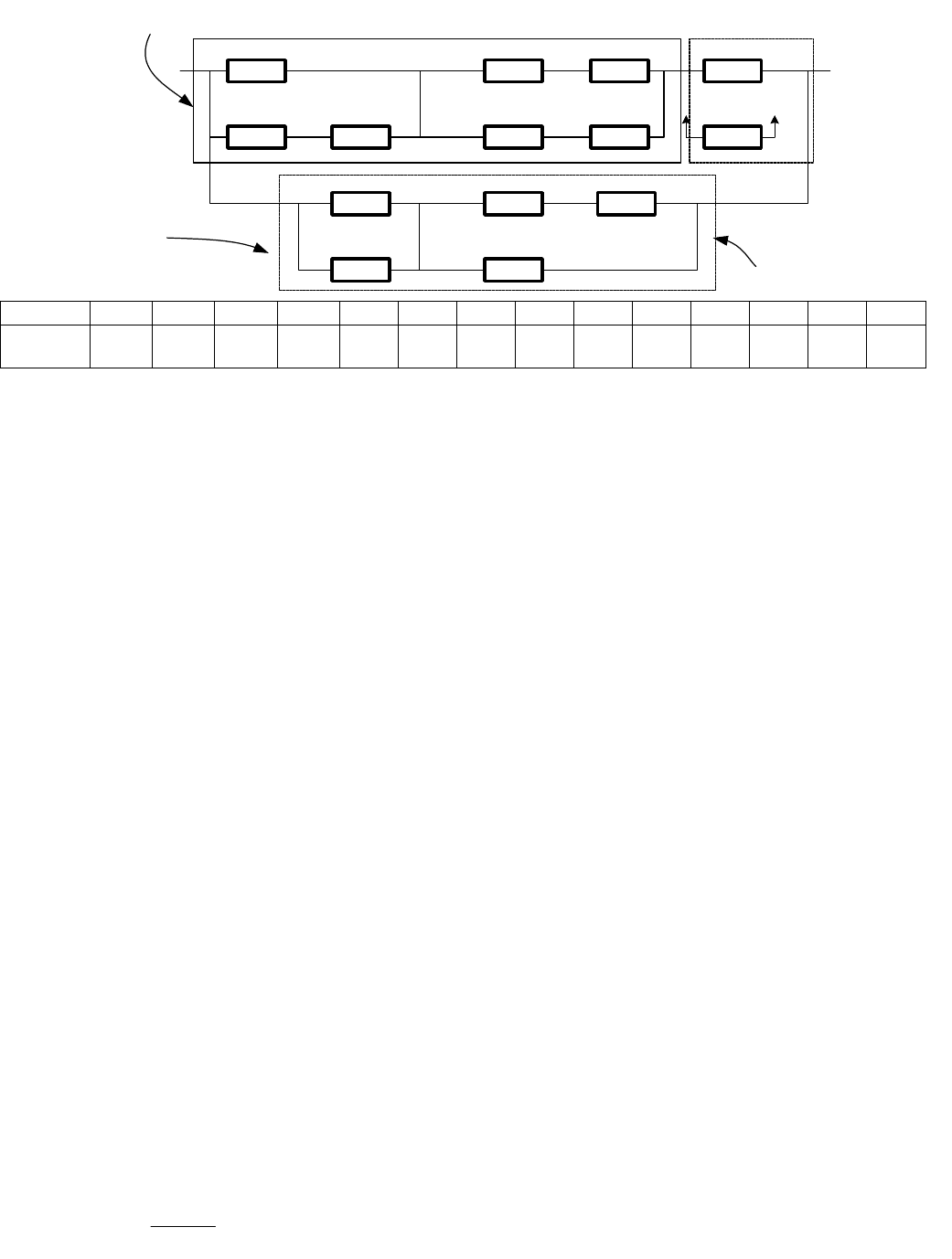
Задана структурная схема для расчета надежности системы, по
известным интенсивностям отказов ее элементов предполагая, что отказы
элементов распределены по экспоненциальному закону. Определить:
- вероятность безотказной работы системы.
- интенсивность отказов узлов (обведены пунктиром)
- среднее время наработки до первого отказа узла системы
На основании выполненных расчетов представить график
узла
(t), выводы и
рекомендации по повышению надежности заданной резервированной
системы.
1
2 3
4
6 7
5
9
8
10
11 13
12 14
а
б
I
II
узел
№ эл-та 1 2 3 4 5 6 7 8 9 10 11 12 13 14
*10
-6
1/
ч
0,95 0,72 1,34 4,11 2,31 0,78 0,88 0,91 0,91 0,17 0,82 0,35 1,67 1,37
Решение.
Определим вероятность безотказной работы системы.
)1)(1(1)(
IIIсист
pptp
)1)(1(1)(
баI
pptp
)***-**)(**-*(
])*1)(*1(1[)]*1)(1(1[)(
76545476321132
7654321
pppppppppppppp
ppppppptp
а
)1()( tetp
t
б
где
98
)***(
)*()]1)(*1(1)][1)(1(1[)(
131412141213
111010111314121110
pppppp
ppppppppptp
II
где
t
i
i
etp
)(
Решим полученные уравнения
ttttttttt
еtttttttеt
еttttttttt
а
eeeeeeeee
eeeeeeeeee
eeeeeеeeeеtp
666666666
6666666666
6666666666
0910.114310.96710.40310.93710.76110.21410.104810.87210.3
0810.84210.66610.10110.39510.00610.28810.07810.03110.21110.4
3110.21110.48810.07810.03410.17210,09510.09510.03410.11072,0
))(()
)(()(
82,1
98
*10
-6
teetetp
ttt
б
666
1082,161082,161082,1
1082,1)10*82,11()(
])1082,1[1})(
{1(1)(
6666
6666666
1082,161082,10910.114310.9
6710.40310.93710.76110.21410.104810.87210.3
tttt
ttttttt
I
eeee
eeeeeeetp
)(
)()***)(*()(
666
666
1039.31072.11067,1
1099.01017,01082,0
13141214121311101011
ttt
ttt
II
eееХ
Хеееpppppppppptp
Вероятность безотказной работы системы:
)})((Х
Х])1082,1[1})(
[1(1{
])1082,1[1})(
[1(1)(
Х)(*)1)(1(1)(
666666
6666
6666666
666666
66666666
666
1039.31072.11067,11099.01017,01082,0
1082,161082,10910.114310.9
6710.40310.93710.76110.21410.104810.87210.3
1082,161082,10910.114310.96710.40310.9
3710.76110.21410.104810.87210.31039.31072.11067,1
1099.01017,01082,0
tttttt
tttt
ttttttt
tttttt
tttttttt
ttt
IIIIIIIIIсист
eеееее
eeee
eeeeeee
eeeeee
eeeeeeееХ
еееpppppptp
Определим интенсивность отказов узла.
)(P
)(
)(
узл
узл
узл
t
tf
t
)(P)(
узл
'
узл
ttf
ttt
ttttt
tttttt
tttt
eee
tetetetete
eeeeee
tetetete
t
666
66666
666666
6666
1038.41071.21066.2
1038.461071.261066.261056.361089.16
1056.31089.11084.11021.41054.21049.2
1084.161021.461054.261049.26
узл
1038.41071.21066.21056.31089.1
1084.11021.41054.21049.2
)(
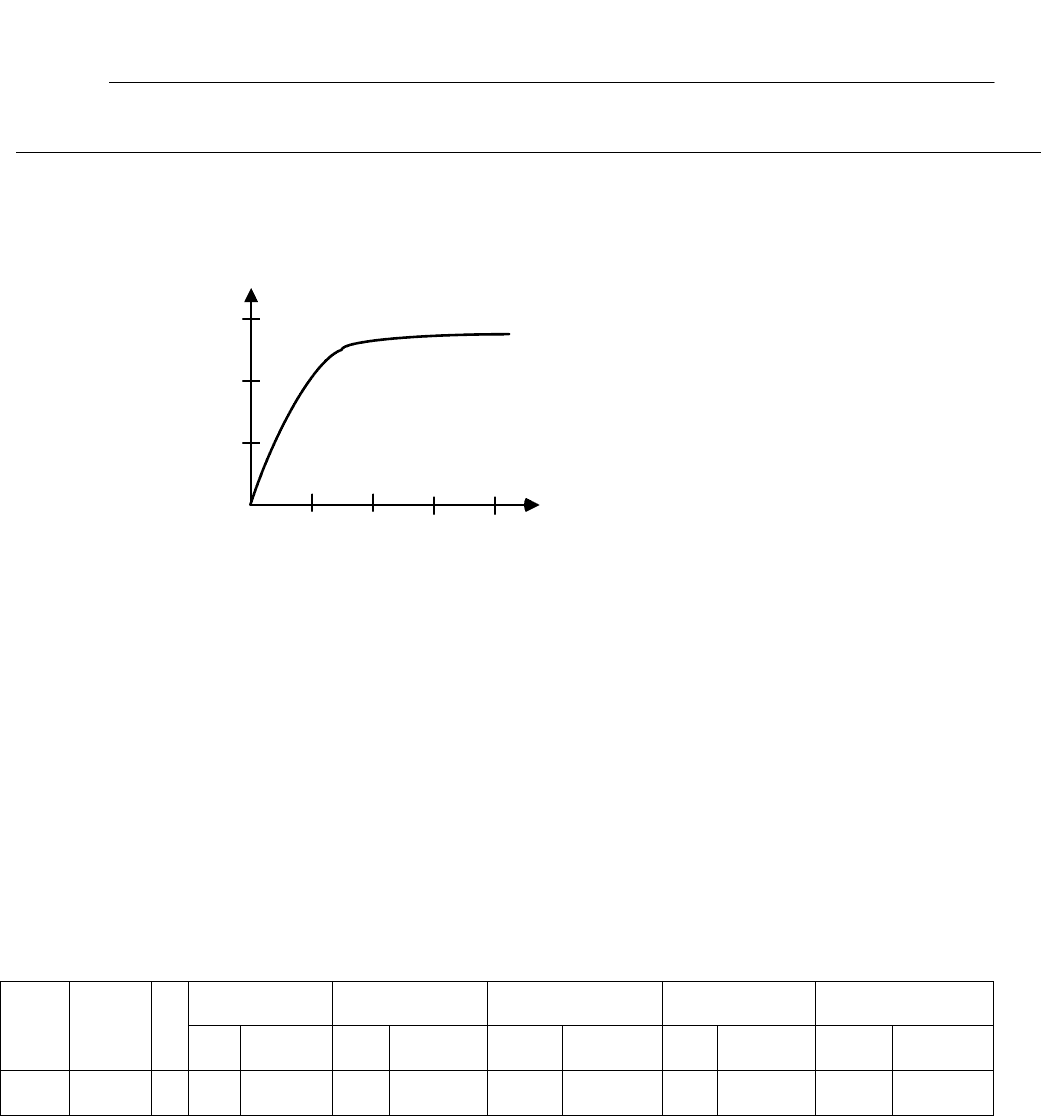
Построим график интенсивности отказов узла:
t
0
Среднее время наработки до первого отказа узла системы:
ч1033.8)
()(
51038.41071.21066.2
0 0
1056.31089.11084.11021.41054.21049.2
узел
666
666666
dteee
eeeeeedttPT
ttt
tttttt
ср
Задача 3.2
Система содержит n групп элементов, каждая j-группа, в свою очередь,
содержит N
j
элементов, причем λ
j
– интенсивность отказов элементов j-
группы. Вероятность безотказной работы системы за время t равна P
k
(t).
Требуется определить число элементов ЗИПа.
P
k
(t) t, ч n
Реле Резисторы Конденсатор Диоды Транзисторы
N
1
λ
1
*10
-5
N
2
λ
2
*10
-5
N
3
λ
3
*10
-5
N
4
λ
4
*10
-5
N
5
λ
5
*10
-5
0,92 17000 5 20 1,4 36 0,2 36 1,6 28 2,5 40 0,95
Определим интенсивность отказов групп элементов.
Λ
гр
= N
i
* λ
i
Λ
реле
= 28*10
-5
Λ
рез
= 7,2*10
-5
Λ
кон
= 57,6*10
-5
Λ
д
= 70*10
-5
Λ
тр
=38*10
-5
Определим вероятность работы групп элементов.
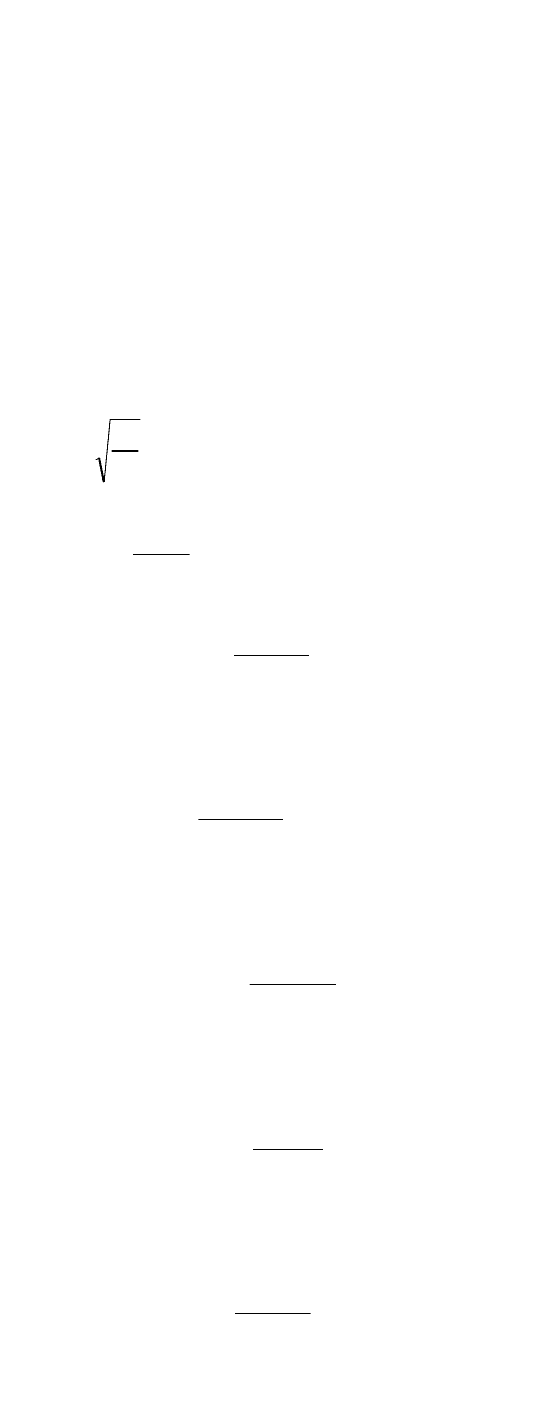
t
гр
гр
еР
00857,0
170001028
реле
5
еР
29,0
рез
Р
5
кон
1059,5
Р
6
д
1079,6
Р
00156,0
тр
Р
Определим вероятность безотказной работы системы при
последовательном соединении без ЗИПа.
n
i
трдконрезi
РРРРРРP
1
15
реле0
1047,1
Определим коэффициент ЗИПа.
n
k
kPP
0
7.5001
0
n
k
P
P
k
Число запасных элементов m определяется подбором при условии:
m
i
i
k
i
t
0
t-
!
)(
eP
Определим число элементов ЗИПа для реле:
m
i
i
i
0
k
!
)76.4(
00857.0P
Следовательно:
8m
947,092,0
Определим число элементов ЗИПа для резисторов:
m
i
i
i
0
k
!
)224,1(
29,0P
3m
951,092,0
Определим число элементов ЗИПа для конденсаторов:
m
i
i
i
0
5
k
!
)792,9(
1059,5P
14m
927,092,0
Определим число элементов ЗИПа для диодов:
m
i
i
i
0
6
k
!
)9,11(
1079,6P
17m
941,092,0
Определим число элементов ЗИПа для транзисторов:
m
i
i
i
0
k
!
)46,6(
00156,0P
10m
933,092,0

4.Оценка и контроль надежности устройств по результатам их
испытаний.
4.1 Оценка надежности устройств.
Задача 4.1.1.
По плану [n, Б, t
0
] испытано n =100 изделий в течение t
0
= 100 часов. При
этом возникло 48 отказов. Известно, что распределение времени до отказа
экспоненциальное. Оценить нижнюю доверительную границу средней
наработки до отказа с вероятностью α
1
= 0,95.
Решение.
Нижняя доверительная граница:
)(2
)](2)[1(
б
1
2
min
TS
Tn
Общая наработка всех элементов:
d
i
i
tdntT
0
0б
)()(S
d – число отказов.
d
i
i
tdntT
0
0б
ч7650)()(S
3
2
min
108,9
76502
]200)[05,0(
Задача 4.1.2.
По плану [n, Б, d] были испытаны 20 электродвигателей. После 6-го
запланированного отказа, наступившего через 180 часов после начала
испытаний, испытания приостановлены. Требуется оценить интенсивность
отказов и найти её верхнюю границу с вероятностью α
2
=0,95.
Решение:
Проведение испытаний организуется в соответствии с планом, в котором
указывается: количество испытуемых изделий, будут ли заменяться
отказавшие изделия и когда испытания необходимо прекратить.
В нашем случае испытания проходят по плану [n,Б,d]
где: n – количество изделий, установленных на испытания;
Б – план испытаний без замены отказавших изделий;
d – прекращение испытаний при возникновении d-го отказа
Предположим, что отказы возникали через равные промежутки времени
t
=180/d. Тогда общая наработка всех элементов:
S(r)=
d
i
d
tdNit
1
*][*
=3150 ч.
где t
d
- время от начала испытаний до d-го отказа
Оценка интенсивности отказов находится по формуле:
)(
1
rS
r
1.59*10
-3
1/ч.

Для определения доверительных границ λ необходимо пользоваться
таблицей квантилей χи-квадрат распределения.
Под доверительным интервалом понимается диапазон значений
параметра, в пределах которого с некоторой вероятностью γ может
находиться его истинное значение. Вероятность γ в этом случае называют
доверительной вероятностью или коэффициентом доверия.
Верхняя граница интенсивности отказов:
)(2
2
)2)((
2
rS
d
= 2,94*10
-3
Задача 4.1.3.
В результате испытаний 12 комплектов аппаратуры были получены
следующие значения наработки на отказ в часах: 16,8; 18,4; 22,3; 22,7; 23,1;
25,5; 26,4; 29,2; 30,3; 32,5; 33,3; 38,1; 42,2. Определить оценку средней
наработки отказа T
*
и дисперсию δ
2
, а также нижнюю границу T и верхнюю
границу δ с вероятностью α=0,9.
Решение.
Проведение испытаний организуется в соответствии с планом, в котором
указывается: количество испытуемых изделий, будут-ли заменятся
отказавшие изделия и когда испытания необходимо прекратить
Целью обработки статистических данных об отказах является
определение закона распределения отказов количественных характеристик
надежности а также периодический контроль качества выпускаемой
продукции.
В нашем случае испытания проходят по плану [n,Б,r]
где: n – количество изделий, установленных на испытания;
Б – план испытаний без замены отказавших изделий;
r – прекращение испытаний по выходу всей аппаратуры из строя;
Т.к. испытания проводились до отказа всех изделий, то оценка
математического ожидания и среднеквадратичного отклонения могут быть
определены из выражения:
n
t
T
n
i
i
1
*
1
)(
1
2
n
Tt
n
i
i
T
*
=27.754 δ=7.466 δ
2
=55.744
В данном случае, величина подчиняется закону распределения
Стьюдента с (n – 1) степенями свободы, где n – число отказов. Поэтому для
того чтобы найти нижнюю границу T и верхнюю границу δ с вероятностью
α=0,9, нам необходимо определить коэффициент доверия γ по таблице
квантилей Стьюдента. Зная γ, находим t
α
и χ
2
.В нашем случае t
α
=1,356,
χ
2
=18,5; поэтому находим границы:
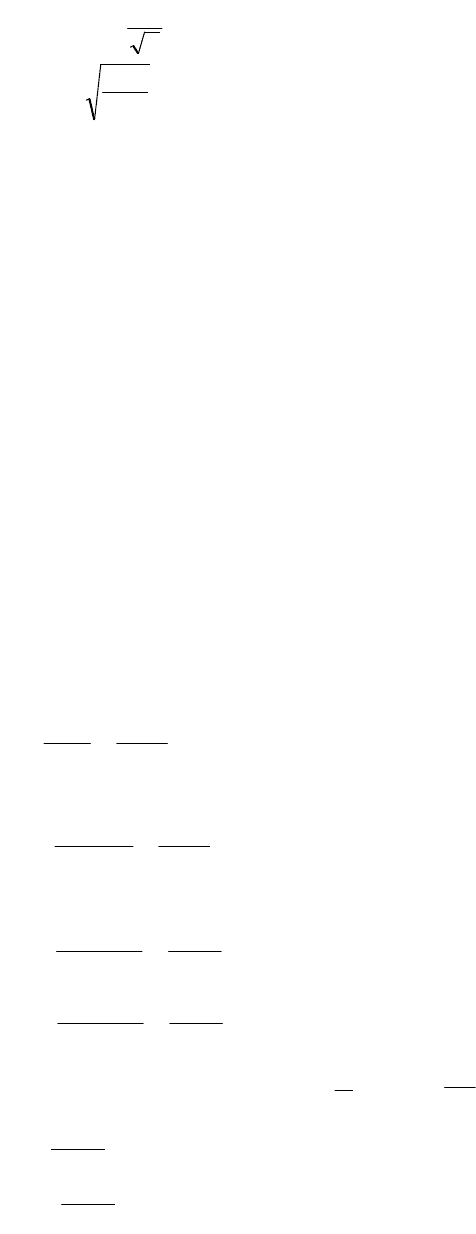
2
max
min
1
n
n
tTT
T
min
=24.946; δ
max
=6.013
Задача 4.1.4.
План испытаний [n, Б, n]. При испытании n = 15 устройств до выхода из
строя получены следующие значения до наработки на отказ в часах: t
1
= 30ч,
t
2
= 35ч, t
3
= 50ч, t
4
= 60ч, t
5
= 80ч, t
6
= 150ч, t
7
=200ч, t
8
=220ч, t
9
= 250ч, t
10
=
280ч, t
11
= 300ч, t
12
= 320ч, t
13
= 380ч, t
14
= 400ч, t
15
= 600ч.
Требуется определить:
1. оценку λ
*
интенсивности отказов λ;
2. верхнюю доверительную границу с доверительной вероятностью α
2
= 0,90;
3. двухсторонний доверительный интервал для λ при α = 0,90 и β
1
= β
2
=0,05;
4. оценку средней наработки до отказа Т и его нижнюю границу с
вероятностью 0,90.
Решение.
3355
15
0
i
i
tt
ч
3
0
1047.4
3355
15
n
i
i
t
n
3
2
)2)(2(
106
6710
3.40
2
t
n
В
Двухсторонний доверительный интервал:
3
2
)30)(95.0(
105.6
6710
8.43
2
t
В
3
2
)30)(05.0(
Н
1075,2
6710
5,18
2
t
Учитывая соотношения
1
T
и
В
T
1
Н
определяем
Т =
6,223
15
3355
часТ
Н
2,153
8,43
6710
Задача 4.1.5
В результате испытаний 100 интегральных схем (ИС), которое
продолжалось t
0
= 5000 ч, вышло из строя 5 ИС с наработкой до отказа в часах
соответственно t
1
= 500, t
2
= 1500, t
3
= 2500, t
4
= 3000, t
5
= 4500. Определить

среднюю наработку на отказ ИС и среднее квадратичное отклонение, полагая,
что срок службы подчиняется нормальному закону.
Решение.
Для вероятностей 0.01, 0.02, 0.03, 0.04, 0.05 найдем квантили u
pi
:
u
p1
= 2,33; u
p2
= -2.5; u
p3
= -1.88; u
p4
= -1.75; u
p5
= -1.64
составим уравнения:
Т-2,33σ =500
Т-2,05σ =1500
Т-1,88σ =2500
Т-1,75σ =3000
Т-1,64σ 4500
Для решения уравнений складываем их: 5Т-9,65σ =12000
Умножая исходные уравнения на коэффициенты при σ и суммируя,
получаем: 9,65Т – 18,91σ = 21570.
Решая уравнения, находим Т = 12298,9 час, σ = 5129 час.
Для оценки точности полученных значений определяем:
42.1
5129
50009.12298
k
5.64443.2
100
64.26306
)()(
2
2
2
kf
n
T
45.231.9
100
64.26306
)()(
3
2
2
kf
n
Откуда
)(T
= 25,4 час,
)(
=1,56 час
Точность определения параметров распределения в условиях данного
примера невысокая. Доверительные интервалы величиной
2
, что
соответствует вероятности ≈ 95%, в данном случае составляют:
12.35129)(2
8.509.12298)(2
TТ
Задача 4.1.6.
План испытаний [n, Б, n]. При испытании n = 10 устройств до выхода из
строя получены следующие значения до наработки на отказ в часах: t
1
= 60ч,
t
2
= 70ч, t
3
= 90ч, t
4
= 160ч, t
5
= 190ч, t
6
= 300ч, t
7
=400ч, t
8
=580ч, t
9
= 800ч, t
10
=
1100ч.
Требуется определить:
1. оценку λ
*
интенсивности отказов λ;
2. верхнюю доверительную границу с доверительной вероятностью α
2
= 0,90;
3. двухсторонний доверительный интервал для λ при α = 0,90 и β
1
= β
2
=0,05;
4. оценку средней наработки до отказа Т и его нижнюю границу с
вероятностью 0,90.
Решение.
3750
10
0
i
i
tt
ч

3
0
1067.2
3750
10
n
i
i
t
n
3
2
)2)(2(
1079,3
7500
4,28
2
t
n
В
Двухсторонний доверительный интервал:
3
2
)20)(95.0(
1018.4
7500
4,31
2
t
В
3
2
)20)(05.0(
Н
1045,1
7500
9,10
2
t
Учитывая соотношения
1
T
и
В
T
1
Н
определяем
Т =
ч375
10
3750
часТ
Н
9,238
4,31
7500
Задача 4.1.7
При испытании электронных приборов по плану [n, Б, d]. Где n=50, а
d=101. через 696 часов испытаний наступил 101-й отказ, время наступления
предыдущих отказов не регистрировалось. Определить среднюю наработку до
отказа и найти его нижнюю с доверительной вероятностью α
1
= 0,99 исходя
из экспоненциального закона распределения отказов.
Решение.
d
i
iii
tdtdtd
0
dб
ч3486]t)(-[n)()5.0()(S
ч86.34
1
)(
1
)(
1
Б
Б
d
dS
T
dS
d
3
Б
1
2
1096,9
2
]2)[1(
S
d
Н
Задача 4.1.8.
Испытано 8 экземпляров ЭЦВМ по плану [n, В, t
0
]. Испытания
продолжались в течении времени t
0
=100 часов, и при этом было
зарегистрировано 8 отказов. Отказы ЭЦВМ мгновенно устранялись. Найти
доверительный интервал значений интенсивности отказов с доверительной
вероятностью для нижней границы
1
=0,9 и для верхней
2
=0,995; определить
доверительную вероятность для двухстороннего интервала.
Решение.
Найдем доверительный интервал и подставив данные получим:
NT
r
2
)2(
2
min
)
1
1(
=5.819*10
-3
