Курсовой проект - Анализ и прогнозирование временного ряда развития уровня жизни населения
Подождите немного. Документ загружается.


Таблица 2.2
Расчет скользящей средней по данным о численности населения
Тюменской области за 1995-2004 гг. по трем уровням
Год Численность
населения,
тыс.чел.
Скользящая
сумма трех
уровней
Скользящая
средняя из трех
уровней
1995 3187 - -
1996 3197 9612 3204
1997 3228 9669 3223
1998 3244 9709 3236
1999 3237 9735 3245
2000 3254 9763 3254
2001 3272 9791 3264
2002 3265 9807 3269
2003 3270 9825 3275
2004 3290 - -
Полученный сглаженный ряд (см. последний столбец Табл.2.2) более
наглядно демонстрирует тенденцию к увеличению уровней численности
населения Тюменской области из года в год, которая в исходном ряду
несколько затушевывалась скачкообразными колебаниями уровней.
Рассматриваемую тенденцию можно наглядно проследить на графике (Рис.2.1):
Рис.2.1
Таблица 2.3
Расчет скользящей средней по данным о среднедушевых денежных
доходах населения Тюменской области за 1995-2004 гг. по трем уровням
Год Среднедушевые
денежные доходы
населения,
тыс.руб.
Скользящая
сумма трех
уровней
Скользящая
средняя из трех
уровней
1995 1085 - -
1996 1202 3571 1190
1997 1284 3520 1173
1998 1034 3235 1078
1999 917 3073 1024
2000 1122 3358 1119
2001 1319 3796 1265
2002 1355 4178 1393
2003 1504 4435 1478
2004 1576 - -
23

Сглаженный ряд (см. последний столбец Табл.2.3) более наглядно
изображает тенденцию к снижению объема среднедушевых денежных доходов
населения до 1999 г., а далее повышение последующих показателей.
Рассматриваемую тенденцию можно наглядно проследить на графике (Рис.2.2):
Рис.2.2
Рассмотренные приемы сглаживания динамических рядов могут
рассматриваться как важное вспомогательное средство, облегчающее
применение других методов и, в частности, более строгих методов выявления
тенденции. Для того чтобы представить количественную модель, выражающую
общую тенденцию изменений уровней динамического ряда во времени,
используется следующий метод.
3. Аналитическое выравнивание ряда динамики.
В этом случае фактические уровни заменяются уровнями, вычисленными
на основании определенной кривой. Предполагается, что она отражает общую
тенденцию изменения во времени изучаемого показателя.
При аналитическом выравнивании ряда динамики закономерно
изменяющийся уровень изучаемого показателя оценивается как функция
времени EMBED Equation.3
)(
ˆ
tfy
t
, где EMBED Equation.3
t
y
ˆ
- уровни
динамического ряда, вычисленные по соответствующему аналитическому
уравнению на момент времени t. Наиболее часто используются следующие
простейшие функции:
1) Линейная функция (2.1):
,
ˆ
10
tbby
t
(2.1)
Данная функция эффективна для рядов динамики, уровни которых
изменяются примерно в арифметической прогрессии.
2) Парабола второго порядка (2.2):
EMBED Equation.3
2
210
ˆ
tbtbby
t
, (2.2)
Данная функция применяется, если вторые разности уровней (ускорения)
более или менее постоянны.
3) Показательная функция (2.3):
,
ˆ
10
t
t
bby
(2.3)
24

Данная функция применяется, если значения уравнений меняются в
геометрической прогрессии, т.е. цепные коэффициенты роста примерно
постоянны.
4) Гиперболическая функция (2.4):
EMBED Equation.3
t
bby
t
1
ˆ
10
, (2.4)
Данная функция применяется, если обнаружено замедленное снижение
уровней ряда.
5) Ряд Фурье (2.5):
).sincos(
ˆ
1
0
ktbktaay
k
m
k
kt
(2.5)
где EMBED Equation.3
t
y
ˆ
– теоретические (выравненные) уровни, t –
условное обозначение времени, EMBED Equation.3
210
,, ааа
– параметры
аналитической функции, k – число гармоник.
Следующим шагом после выяснения характера кривой развития является
определение ее параметров. Для этого существует несколько способов:
1) Элементарный метод определения параметров уравнения тренда
состоит в решении системы уравнений по известным уровням ряда динамики.
Если дан ряд динамики, то, приняв условные обозначения времени через t и
две точки (конечный и начальный уровни), можно построить уравнение прямой
по этим двум точкам.
В результате при выравнивании по прямой линии EMBED Equation.3
tbby
t 10
ˆ
, получают EMBED Equation.3
,0)(
10
tbby
откуда EMBED
Equation.3
.
10
ytbnb
если применить это требование к каждой из двух
частей ряда, то, вычисляя для каждой части динамического ряда EMBED
Equation.3
t
и EMBED Equation.3
y
, получают два уравнения с двумя
неизвестными. В результате решения уравнений находят параметры.
Отрицательным моментом в таком моделировании тренда являются
разные числовые выражения параметров в различных точках их определения.
2) Метод средних значений (линейных отклонений) заключается в
следующем: ряд расчленяется на две примерно равные части и вводится
требование, чтобы сумма выравненных значений в каждой части совпала с
суммой фактических значений, другими словами чтобы сумма отклонений
фактических данных от выравненных равнялась нулю.
Данный метод прост и требует минимального количества вычислений.
Его недостаток заключается в том, что при произвольном расчленении ряда на
две части могут получиться разные результаты.
25

3) Метод конечных разностей основан на свойствах различных
кривых, применяемых при выравнивании.
Пусть дан ряд динамики у
t
, который описывается полиномом р-й степени.
Для полинома вычисляются следующие разности:
постоянные первые разности: EMBED Equation.3
ttt
yy
1
)1(
;
нулевые вторые разности: EMBED Equation.3
tt
t
)1(
1
)1(
)2(
;
и т.д.
Формула для расчета уровней ряда динамики при равных или почти
равных первых разностях имеет вид (2.6):
.
1)1(
tyy
t
(2.6)
Если вторые разности практически равны, то вычисляя коэффициенты
параболы второго порядка, получают тренд ряда динамики (2.6):
EMBED Equation.3
,
224
1
2
)2(
1)1()2(
2
tt
n
yy
t
(2.7)
где EMBED Equation.3
t
y
- выравненное значение ряда динамики;
EMBED Equation.3
y
- средний уровень ряда динамики;
EMBED Equation.3
)1(
- средняя арифметическая первых разностей;
EMBED Equation.3
)2(
- средняя арифметическая вторых разностей;
n – число уровней;
t – условное обозначение времени.
4) Метод наименьщих квадратов (МНК) используется при расчете
параметров уравнений тренда. Сущность этого метода заключается в
нахождении параметров модели, при которых минимизируется сумма
квадратов отклонений эмпирических значений результативного признака от
теоретических, полученных по выбранному уравнению, т.е. EMBED Equation.3
.min)
ˆ
(
2
t
yy
Выравнивание рядов динамики по некоторым аналитическим функциям и
использование методов определения их параметров приведены ниже.
1. Выравнивание по линейной функции.
Нужно определить аналитическое выравнивание, иными словами
составить уравнение тренда, по данным о численности населения Тюменской
области за 1995-2004 гг. В качестве гипотетической функции теоретических
уровней можно принять прямую EMBED Equation.3
tbby
t 10
ˆ
.
Для определения параметров аналитического уравнения при
выравнивании данного ряда можно использовать МНК. Система нормальных
уравнений в данном случае имеет вид (2.8):
26

EMBED Equation.3
n
i
n
i
n
ii
n n
ii
tbtbty
tbnby
1
2
1
1
0
1
1 1
10
.
;
(2.8)
В данном случае отсчет времени ведется от середины ряда, так как число
уровней ряда четное (n=10). Два серединных момента следует обозначить как -
1 и +1, а все последующие и предыдущие, соответственно, через EMBED
Equation.3
5;4;3;2
. Следовательно сумма показателей времени будет равна
нулю ( EMBED Equation.3
0
1
n
i
t
) и система нормальных уравнений
преобразуется следующим образом (2.9):
EMBED Equation.3
n
n
i
n
ii
i
n
ii
n
i
n
i
t
ty
btbty
y
n
y
bnby
1
1
2
1
1
2
1
1
00
1
.
;
1
(2.9)
Расчеты параметров уравнений прямой приведены в Табл.2.4:
EMBED Equation.3
Таблица 2.4
Расчет теоретических уровней линейного тренда от середины ряда
Год Численность
населения,
тыс.чел.
y
i
Условные
обозначения
периодов,
t
i
t
i
2
y
i
t
i
Выравненные
уровни,
EMBED
Equation.3
y
ˆ
1 2 3 4 5 6
1995 3187 -5 25 -15935 3199,36
1996 3197 -4 16 -12788 3208,36
1997 3228 -3 9 -9684 3217,37
1998 3244 -2 4 -6488 3226,38
1999 3237 -1 1 -3237 3235,39
2000 3254 1 1 3254 3253,41
27

2001 3272 2 4 6544 3262,42
2002 3265 3 9 9795 3271,43
2003 3270 4 16 13080 3280,44
2004 3290 5 25 16450 3289,45
Итого 32444 0 110 991 32444,01
Подставив данные суммы (графы 2, 4, и 5) в указанные уравнения можно
получить, при n=14, следующие результаты:
EMBED Equation.3
;4,3244
10
32444
0
b
EMBED
Equation.3
.009,9
110
991
1
b
По рассчитанным параметрам записывается уравнение прямой ряда
динамики:
.009,94,3244
ˆ
ty
t
(2.10)
В графе 6 Табл.2.4 приведены теоретические уровни, рассчитанные по
уравнению (2.10) (путем подстановки в него значений t
i
).
Правильность расчета уровней выравниваемого ряда динамики может
быть проверена следующим образом: сумма значений эмпирического ряда
должна совпадать с суммой вычисленных уровней выравненного ряда, т.е.
EMBED Equation.3
n
i
t
n
i
i
i
yy
11
ˆ
(итоги гр. 2 и 6).
Коэффициент регрессии в уравнении (2.10) равен EMBED Equation.3
009,9
1
b
и характеризует среднее годовое изменение (уменьшение)
численности населения Тюменской области за 1995-2004 гг.
2. Выравнивание по параболе второго порядка.
Нужно определить аналитическое выравнивание, иными словами
составить уравнение тренда, по данным о среднедушевых денежных доходах
населения Тюменской области за 1995-2004 гг. В качестве гипотетической
функции теоретических уровней можно принять прямую
2
210
ˆ
tbtbby
t
.
Параметры искомого уравнения тренда (
210
,, bbb
) находятся при решении
системы нормальных уравнений, полученных методом наименьших квадратов
(МНК). Отсчет уровней, как и в предыдущем случае, ведется от середины ряда.
Необходимые расчеты приведены в Табл.2.5.
Следовательно сумма показателей времени будет равна нулю (
0
1
n
i
t
) и
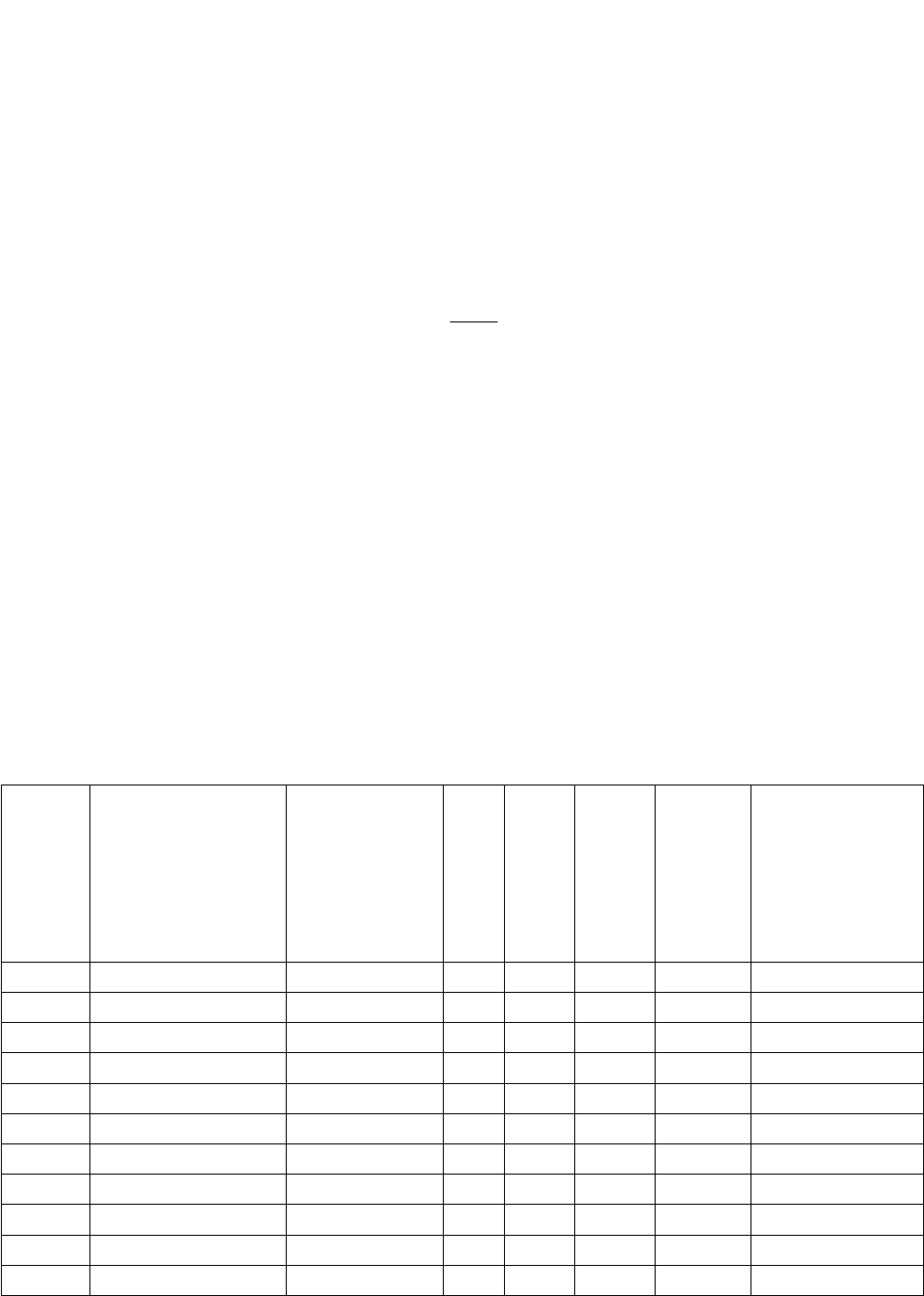
система нормальных уравнений преобразуется следующим образом (2.11):
28
n n
i
n
iii
n n
iii
n n
ii
n n n
iiiii
n
i
n
i
n
i
n
ii
n
i
n
i
n
i
tbtbty
tbty
tbnby
tbtbtbty
tbtbtbty
tbtbbny
1 1
4
2
1
2
0
2
1 1
2
1
1 1
2
20
1 1 1
4
2
3
1
2
0
2
1
3
2
1
2
1
1
0
1
1
2
2
1
10
1
.
;
;
.
;
;
(2.11)
При подстановке в (2.11) рассчитанных значений, которые получены в
Табл.2.5, получаются следующие результаты:
.1958110145023
;1104651
;1101012398
20
1
20
bb
b
bb
Затем несложно найти
1
b
:
.28,42
110
4651
1
b
При совместном решении первого и третьего уравнения системы можно
найти:
56,11
2
b
и
.64,1112
0
b
После нахождения всех искомых параметров можно составить уравнение
тренда (2.12):
(2.12)
В графе 8 Табл.2.5 приведены теоретические уровни, рассчитанные по
уравнению (2.12) (путем подстановки в него значений t
i
).
Таблица 2.5
Выравнивание ряда динамки по параболе второго порядка от середины ряда
Год Среднедушевые
денежные
доходы
населения,
тыс.руб.
y
i
Условные
обозначения
периодов,
t
i
t
i
2
t
i
4
y
i
t
i
y
i
t
i
2
Выравненные
уровни,
y
ˆ
1 2 3 4 5 6 7 8
1995 1085 -5 25 625 -5425 27125 1190,24
1996 1202 -4 16 256 -4808 19232 1128,48
1997 1284 -3 9 81 -3852 11556 1089,84
1998 1034 -2 4 16 -2068 4136 1074,32
1999 917 -1 1 1 -917 917 1081,92
2000 1122 1 1 1 1122 1122 1166,48
2001 1319 2 4 16 2638 5276 1243,44
2002 1355 3 9 81 4065 12195 1343,52
2003 1504 4 16 256 6016 24064 1466,72
2004 1576 5 25 625 7880 39400 1613,04
29
.56,1128,4264,1112
ˆ
2
tty

Итого 12398 0 110 1958 4651 145023 12398
Сравнивая теоретические уровни с эмпирическими, можно отметить, что
они очень схожи, а их суммы равны. Таким образом, парабола второго порядка
является подходящей функцией для отражения основной тенденции изменения
уровней (тренда) за исследуемый промежуток времени.
2.2. Измерение колеблемости в рядах динамики
Если рассматривать динамические ряды месячных уровней производства
молока, мяса, ряды объема продаж разных видов обуви или одежды, ряды
заболеваемости населения, выявляются регулярно повторяющиеся из года в год
сезонные колебания уровней. В силу солнечно-земных связей частота полярных
сияний, интенсивность гроз, те же изменения урожайности отдельных
сельскохозяйственных культур и ряд других процессов имеют тциклическую
10–11 летнюю колеблемость. Колебания числа рождений, связанные с потерями
в войне, повторяются с угасающей амплитудой через поколения, то есть через
20–25 лет.
Тенденция динамики связана с действием долговременно существующих
факторов, причин и условий развития, хотя, после какого-то периода условия
могут измениться и породить уже другую тенденцию развития изучаемого
объекта. Колебания же, напротив, связаны с действиями краткосрочных или
циклических факторов, влияющих на отдельные уровни динамического ряда, и
отклоняющих уровни тенденции то в одном, то в другом направлении.
При статистическом изучении динамики необходимо четко разделить два
ее основных элемента – тенденцию и колеблемость, чтобы дать каждому из них
количественную характеристику с помощью специальных показателей.
Выделяют следующие типы колебаний уровней ряда:
тренд (является долговременной компонентой ряда динамики);
циклические колебания (являются долгопериодическими);
сезонные колебания (обнаруживаются в рядах, где данные
приведены за кварталы или месяцы);
случайные колебания (обнаруживаются в результате действия
большого числа относительно слабых второстепенных факторов).
При измерении колеблемости уровней в рядах динамики могут
использоваться следующие показатели:
1. Размах, или амплитуда, отклонений отдельных уровней от их
средней (расчет ведется по модулю) (2.13) или от тренда (2.14):
(2.13)
(2.14)
30
;yyR
i
.
ˆ
yyR
i

2. Среднее линейное отклонение (расчет ведется по модулю) является
среднеарифметической из абсолютных значений отдельных уровней
от общей средней (2.15) или от тренда (2.16):
(2.15)
(2.16)
3. Среднее квадратическое отклонение отдельных уровней от
общей средней (2.17) или от тренда (2.18):
(2.17)
(2.18)
4. Относительный показатель колеблемости уровней ряда динамики,
аналогичный коэффициенту вариации (2.19):
%.100
y
V
Данные для расчета показателей, характеризующих колеблемость в ряду
динамики по данным о численности населения Тюменской области за 1995-
2004 гг., приведены в Табл.2.6:
Таблица 2.6
Данные для расчета показателей колеблемости
Год Численность
населения,
тыс.чел.
i
y
Выравненные
уровни
y
ˆ
yy
ˆ
2
ˆ
yy
yy
2
)( yy
1995 3187 3199,36 -12,36 152,77 -57,4 3294,76
1996 3197 3208,36 -11,36 129,05 -47,4 2246,76
1997 3228 3217,37 10,63 113,00 -16,4 268,96
1998 3244 3226,38 17,62 310,46 -0,4 0,16
1999 3237 3235,39 1,61 2,59 -7,4 54,76
2000 3254 3253,41 0,59 0,35 9,6 92,16
2001 3272 3262,42 9,58 91,78 27,6 761,76
31
;
n
yy
d
i
i
.
ˆ
n
yy
d
i
i
;
2
n
yy
i
.
ˆ
2
n
yy
i
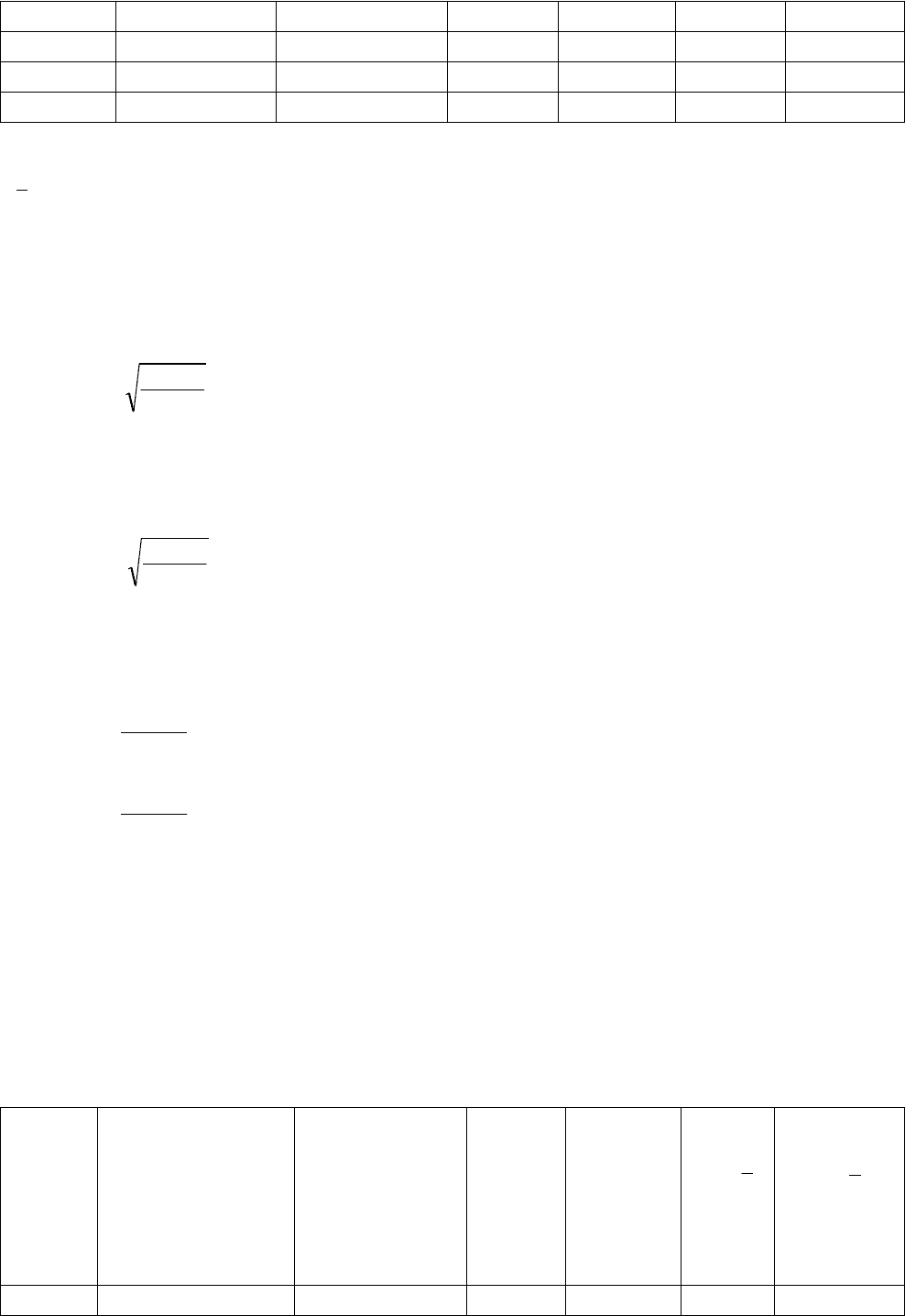
2002 3265 3271,43 -6,43 41,34 20,6 424,36
2003 3270 3280,44 -10,44 108,99 25,6 655,36
2004 3290 3289,45 0,55 0,30 45,6 2079,36
Итого 32444 32444,01 950,63 9878,4
Для расчета предпоследней графы потребуются следующие данные:
4,32441032444 y
тыс.чел.
Таким образом, показатели, характеризующие колеблемость в ряду
динамики равны:
– среднее квадратическое отклонение отдельных уровней от тренда
рассчитывается по формуле (2.18):
75,9
10
63,950
1
тыс.чел.
– среднее квадратическое отклонение отдельных уровней от среднего
уровня рассчитывается по формуле (2.17):
43,31
10
4,9878
2
тыс.чел.
– относительный показатель колеблемости рассчитывается по формуле
(2.19):
%30,0%100
4,3244
75,9
V
%97,0%100
4,3244
43,31
V
Данные для расчета показателей, характеризующих колеблемость в ряду
динамики по данным о среднедушевых денежных доходах населения
Тюменской области за 1995-2004 гг., приведены в Табл.2.7:
Таблица 2.7
Данные для расчета показателей колеблемости
Год Среднедушевые
денежные
доходы
населения,
тыс.руб.
i
y
Выравненные
уровни
y
ˆ
yy
ˆ
2
ˆ
yy
yy
2
)( yy
1995 1085 1190,24 -105,24 11075,46 -154,8 23963,04
32
