Курсовая работа - Сведение матричной игры к задаче линейного программирования

Подождите немного. Документ загружается.

Первая группа ограничений относится к объёмам потребляемых химических

компонентов:

Sx 



1

ni ,1

, (3.26)

где

– объём i-го химического компонента, которым располагает фирма в

начале планируемого периода.

Вторая группа ограничений отражает требование, заключающееся в том,

чтобы запланированный выпуск продукции хотя бы в минимальной степени

удовлетворял имеющийся спрос на каждый из химических продуктов, т.е.

Dx 



1

mj ,1

. (3.27)

где

– минимальный спрос на продукцию

в течение планируемого

периода.

Третья группа ограничений связана с технологическими особенностями,

которые необходимо принимать во внимание при приготовлении смеси, например

простое ограничение, определяемое некоторыми минимально допустимыми

значениями, отношение между объёмами двух химических компонентов в

процессе получения продукта



1

или





 ji

где

– некоторая заданная константа.

Обозначим через

доход с единицы продукции

, запишем целевую

функцию:

ijij

xPZ







max

. (3.28)

Пример (п.3.6)

Задача о раскрое или минимизации обрезков.

Данная задача состоит таких технологических планов раскроя, при которых

получается необходимый комплекс заготовок, а отходы (по длине, площади,

объёму, массе или стоимости) сводятся к минимуму.

Например, продукция бумажной фирмы выпускается в виде бумажных

рулонов стандартной ширины

. По специальным заказам потребителей фирма

поставляет рулоны других размеров, для этого производится разрезание

стандартных рулонов. Типичные заказы на рулоны нестандартных размеров могут

включать

видов шириной

 

mil

,1

. Известна потребность в нестандартных

каждого вида, она равна

. Возможны

различных вариантов построения

технологической карты раскроя рулонов стандартной ширины

на рулоны

длиной

Обозначим через

количество рулонов i-го вида, получаемых при раскрое

единицы стандартного рулона по j-му варианту. При каждом варианте раскроя на

каждый стандартный рулон возможны потери, равные

. К потерям следует

относить также избыточные рулоны нестандартной длинны

, получаемые при

различных вариантах раскроя

nj ,1

В качестве переменных следует идентифицировать количество стандартных

рулонов, которые должны быть разрезаны при j-м варианте раскроя. Определим

переменную следующим образом:

– количество стандартных рулонов,

разрезаемых по варианту

nj ,1

Целевая функция – минимум отходов при раскрое







yxPZ

min

(3.29)

Ограничение на удовлетворение спроса потребителя







jiji

yxab

0

. (3.30)

Пример (п.3.7)

Многостойный коммерческий арбитраж.

В сфере деятельности, связанной с валютными и биржевыми операциями, а

также коммерческими сделками контрактного характера, возможны различные

рода трансакции, позволяющие извлекать прибыль на разнице в курсе валют.

Такого рода трансакции называются коммерческим арбитражем.

Представим себе коммерсанта (условно назовём его N), имеющего

возможность реализовать многосторонний коммерческий арбитраж.

Предположим, что число валютных рынков, вовлечённых в трансакционную

деятельность коммерсанта N, равняется шести, а максимальное число возможных

трансакций равняется девяти. Подробные данные характеризующие

рассматриваемую задачу, приведены в табл. 3.2.

Таблица 3.2

Многосторонний коммерческий арбитраж

Валютный

номинал

Тип трансакции

Возмож-

ность

рынка

1 2 3 4 5 6 7 8 9

III

1

0

Размер

трансакции

При трансакции

продажа единицы валютного наминала (ценных бумаг) II

позволяет приобрести

валютного наминала I. При трансакции

взамен

единицы валютного наминала I можно получить

единиц валютного наминала

III и

валютного наминала VI. Остальные трансакции расшифровываются

аналогично. Значения

могут быть дробными. Заметим, что при любой

трансакции

 

5,4,3,2,1ix

каждый из валютных номиналов можно обменять на

валютный номинал I. Следует обратить внимание на правило выбора знака перед

показателями в табл. 3.2. Чтобы отличить куплю от продажи, буду соответственно

использовать знаки «плюс» и «минус» перед показателями, характеризующими

данную трансакцию.

Рассмотрим идеализированный случай, когда все трансакции коммерсанта N

выполняются одновременно. Ограничения определяются единственным

требованиям – трансакция возможна лишь при условии, если коммерсант N

располагает наличными ценными бумагами. Другими словами, количество

проданных ценных бумаг не должно количество приобретённых. Данные

ограничения имеют вид

.9,1,0

97675

8584

94983

8387372

9296261

76515414313212111













xxrx

xrx

xrxx

xrxrx

xxxrxrxrxrxr

Пусть целевая функция представляет собой чистый доход, выраженный в

единицах валютного номинала I, т.е. задача состоит в том, чтобы

76515414313212111max

xxxrxrxrxrxrZ 

Пример (п.3.8)

Транспортная задача.

Имеет три поставщика и четыре потребителя однородной продукции.

Известны затраты на перевозку груза от каждого поставщика каждому

потребителю. Обозначим их

4,1;3,1  ji

. Запасы грузов у поставщиков

равны

3,1, ia

. Известны потребности каждого потребителя

4,1, jb

. Будем

считать, что суммарные потребности равны суммарным запасам:







1 i

Требуется составить такой план перевозок, чтобы обеспечить минимальные

суммарные затраты при полном удовлетворении потребностей.

Введу переменную

– количество груза, перевозимого от i-го поставщика

j-му потребителю.

Ограничения задачи выглядят следующим образом:

 потребности всех потребителей должны быть удовлетворены

полностью:













4342414

3332313

2322212

13 12111

bxxx

(3.31)

или в общем виде:

bx 





4,1j

 груз от поставщика должен быть вывезен полностью:













;

334333231

224232 221

114131211

axxxx

(3.32)

или в общем виде:

ax 





3,1i

;

 условие не отрицательности переменных:

0

3,1i

4,1j

Целевая функция должна минимизировать суммарные затраты на перевозку:

xcZ





min

. (3.33)

Количество поставщиков и потребителей в общем случае может быть

произвольным

 

2

Я рассмотрел восемь примеров типовых задач линейного программирования.

Обобщая из, можно сделать следующие выводы.

1. Ограничения в задачах линейного программирования могут быть

выражены как равенствами, так и неравенствами.

2. Линейная функция может стремиться как к максимуму, так и к минимуму.

3. Переменные в задачах всегда неотрицательны.

Из любой из вышеперечисленных задач можно перейти к канонической

(основной) задаче линейного программирования.

3.3. Графическое решение задачи линейного программирования.

Графический способ решения задачи линейного программирования

целесообразно использовать для:

 решения задач с двумя переменными, когда ограничения выражены

неравенствами;

 решение задач со многими переменными при условии, что в их

канонической записи содержится не более двух переменных.

Запишем задачу линейного программирования с двумя переменными :

целевая функция:

2211max

xcxcZ 

(3.34)

ограничения:













;

2211

2222121

1212111

mmm

bxaxa



(3.35)

.0;0

 xx

(3.36)

Каждое из неравенств (3.35) – (3.36) системы ограничений задачи

геометрически определяет полуплоскость соответственно с граничными прямыми

iii

bxaxa 

2211

;

 

mi ,1

;

x

;

x

. В том случае, если система неравенств

(3.35) – (3.36) совместна, область её решений есть множество точек,

принадлежащих всем указанным полуплоскостям. Так как множество точек

пересечения данных полуплоскостей – выпуклое, то областью допустимых

решений является выпуклое множество, которое называется многоугольником

решений. Стороны этого многоугольника лежат на прямых, уравнения которых

получаются из исходной системы ограничений с заменой знаков неравенств на

знаки равенств.

Областью допустимых решений системы неравенств (3.35) – (3.36) может

быть:

 выпуклый многоугольник;

 выпуклая многоугольная неограниченная область;

 пустая область;

 луч;

 отрезок;

 единственная точка.

Целевая функция (3.34) определяет на плоскости семейство параллельных

прямых, каждой из которых соответствует определённое значение

Вектор

 

,ccC 

с координатами

, перпендикулярный этим прямым,

указывает направление наискорейшего возрастания

, а противоположный

вектор – направление убывания

Если в одной и той же системе координат изобразить область допустимых

решений системы неравенств (3.35) – (3.36) и семейство параллельных прямых

(3.34), то задача определения максимума функции

сведётся к нахождению в

допустимой области точки, через которую проходит прямая из семейства

constZ 

, и которая соответствует наибольшему значению параметра

Эта точка существует тогда, когда многоугольник решений не пуст и на нем

целевая функция ограничена сверху. При указанных условиях в одной из вершин

многоугольника решений целевая функция принимает максимальное значение.

Для определения данной вершины построим линию уровня

2211

 xcxcZ

проходящую через начало координат и перпендикулярную вектору

 

,ccC 

, и

буде передвигать её в направлении вектора

 

,ccC 

до тех пор, пока она не

коснётся последней крайней (угловой) точки многоугольника решений.

координаты указанной точки и определяют оптимальный план данной задачи.

Заканчивая рассмотрение геометрической интерпретации задачи (3.34) –

(3.36), отмечу, что при нахождении её решения могут встретится случаи,

изображенные на рис. 3.1 – 3.4.

Рис. 3.1 характеризует такой случай, когда целевая функция принимает

максимальное значение в единственной точке А. Из рис. 3.2 видно, что

максимальное значение целевая функция принимает в любой точке отрезка АВ.

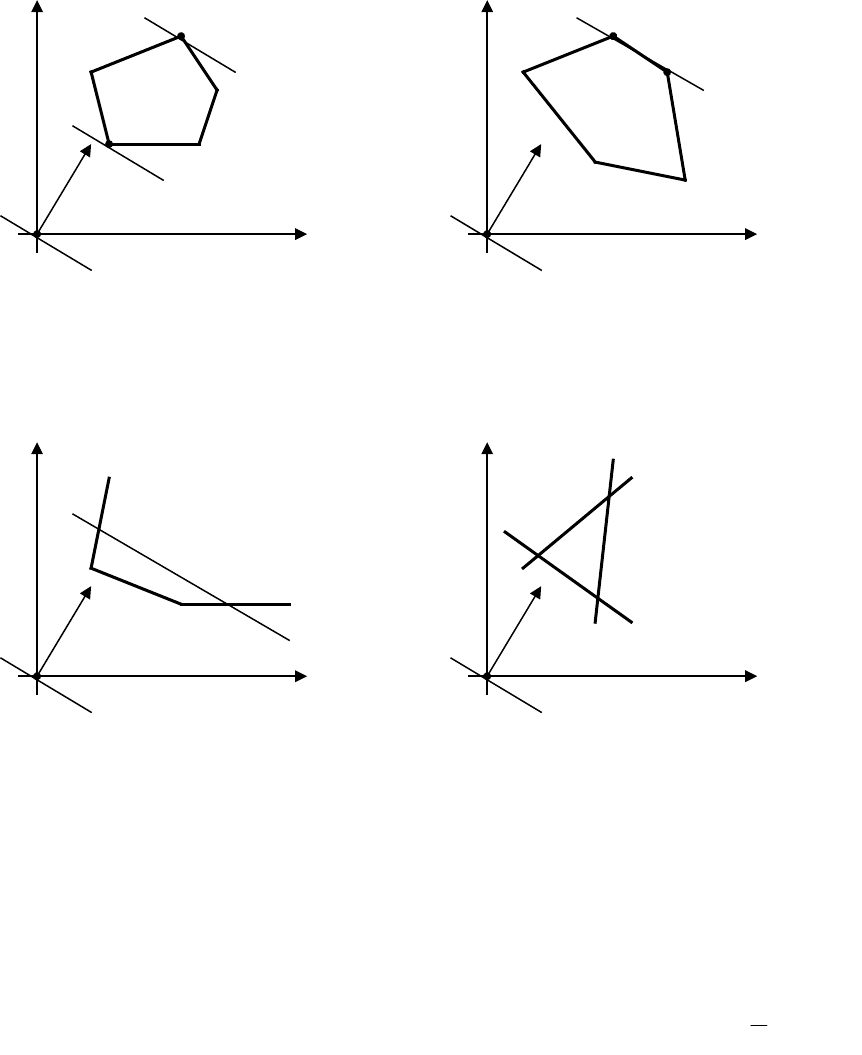
Рис. 3.1. Оптимум Рис. 3.2. Оптимум Функция Z

Функция Z достижим в точке А достигается в любой точке [AB]

Рис. 3.3. Оптимум Рис. 3.4. Область допустимых

Функция Z недостижим решений – пустая область

На рис. 3.3 изображен случай, когда максимум недостижим, а на рис. 3.4 –

случай, когда система ограничений задачи несовместна. Отмечу, что нахождение

минимального значения Z при данной системе ограничений отличается от

нахождения её максимального значения при тех же ограничениях лишь тем, что

линия уровня Z передвигается не в направлении вектора

 

,ccC 

, а в

противоположном направлении. Таким образом, отмеченные выше случаи,

встречающиеся при нахождении максимального значения целевой функции,

имеют место и при определении её минимального значения.

Для практического решения задачи линейного программирования (3.34) –

(3.36) на основе её геометрической интерпретации необходимо следующее:

1. Построить прямые, уравнения которых получается в результате замены в

ограничениях (3.34) – (3.36) знаков неравенств на знаки равенств.

Z=0



max

Z=0

2. Найти полуплоскости, определяемые каждым из ограничений задачи.

3. Определить многоугольник решений.

4. Построить вектор

 

,ccC 

5. Построить прямую

2211

 xcxcZ

, проходящую через начало координат и

перпендикулярную вектору

6. Передвигать прямую

2211

xcxcZ 

в направлении вектора

, в результате

чего-либо находят точку (точки), в которой целевая функция принимает

максимальное значение, либо устанавливают неограниченность функции в этой

точке.

4. Симплекс-метод.

Для начала работы требуется, чтобы заданная система ограничений

выражалась равенствами, причём в этой системе ограничений должны быть

выделены базисные неизвестные. Решение задачи симплекс-методом распадается

на ряд шагов. На каждом шаге от данного базиса Б переходят к другому, новому

базису Б

с таим расчётом, чтобы значение функции Z уменьшилось, т.е.

ZZ 

Для перехода к новому базису из старого базиса удаляется одна из переменных и

вместо нее вводится другая из числа свободных. После конечного числа шагов

находится некоторый базис Б

(k)

, для которого

)( k

есть искомый минимум для

линейной функции Z, а соответствующее базисное решение является

оптимальным либо выясняется, что задача не имеет решения.