Курсовая работа - Сведение матричной игры к задаче линейного программирования
Подождите немного. Документ загружается.


Каждая матричная игра с нулевой суммой имеет, по крайней мере, одно
решение, возможно в области смешанных стратегий, то есть существуют
стратегии
X
и
Y
, оптимальные для обоих игроков, причём
);();(maxmin);(minmax
YXMYXMYXM
. (1.9)
Число
);(
YXMV
называют ценой игры.
Примечание. Нулевая сумма означает, что выигрыш одного игрока равен
проигрышу другого.
Из основной теоремы следует, что каждая конечная игра имеет цену и она
лежит между нижней и верхней ценами игры (1.8).
И, если один из игроков придерживается своей оптимальной стратегии, то
выигрыш (проигрыш) его остаётся неизменным независимо от тактики другого
игрока, если, конечно, последний не выходит за пределы своих «полезных»
стратегий, иначе выигрыш (проигрыш) возрастает.
Это означает выполнение неравенств
m
i
iij
Vxa
1
nj ,1
, (1.10)
Vya
n
j
jij
1
,
mi ,1
. (1.11)
Примечание. Эти неравенства будут необходимы при сведении матричной
игры к задаче линейного программирования.
13

2. Элементарные методы решения матричных игр
22
,
m2
,
2m
.
2.1. Игра
22
.
Наиболее простой матричной игрой является игра
22
, в которой игроки
имеют по две чистых стратегии.
Пусть матрица такой игры
2221
1211
aa
aa
H
. (2.1)
Если седловой точки нет, то решением игры являются смешанные стратегии
21
; xxX
(2.2)
21
; yyY
. (2.3)
Согласно основной теореме теории игр, применение оптимальной стратегии
X
игроком А обеспечивает получение выигрыша V при любых стратегиях
игрока В. Сказанное приводит к системе уравнений:
Vxaxa
Vxaxa
222112
221111
Кроме того,
1
21
xx
.
Решение этих уравнений даёт:
21122211
2122
1
aaaa
aa
x
, (2.4)
21122211
1211
2
aaaa
aa
x
, (2.5)
21122211
21122211
aaaa
aaaa
V
. (2.6)
Аналогично, применение оптимальных стратегии
21
; yyY
обеспечивает
проигрыш V игроку В при любых стратегиях А, что приводит к системе
.1
,
,
21
222121
212111
yy
Vyaya
Vyaya
(2.7)
Ее решение даётся формулами
,
21122211
1222
1
aaaa
aa
y
(2.8)
14
При стратегии В
1
игрока В,
При стратегии В
2
игрока В.
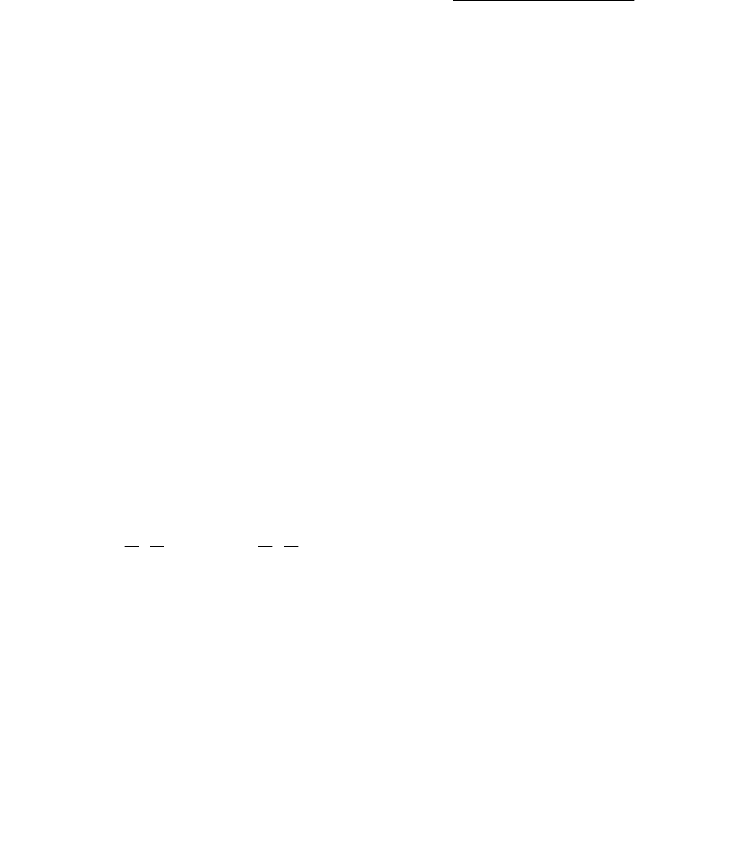
.
21122211
2111
1
aaaa
aa
y
(2.9)
Пример (п.2.1)
Во многих учебниках приводится пример игры в «орла и решку», суть
которой состоит в следующем. Каждый из двух партнёров, не зная хода другого,
кладёт свою монету орлом или решкой вверх и при совпадении наименований
второй игрок (В) платит первому (А) единицу, а при несовпадении первый платит
второму. Очевидно платёжная матрица такой игры будет:
.
11
11
H
Седловой точки нет. Тогда, согласно формул: (2.4), (2.5), (2.6), (2.8) и (2.9),
оптимальными стратегиями будут
2
1
;
2
1
X
,
2
1
;
2
1
Y
, цена игры
0V
.
Примечание. Отмечу, что матрица этой игры симметрична и на первый
взгляд может показаться, что симметричность матрицы ведёт к справедливой
(безобидной) игре для обоих игроков. На самом деле симметричность не
гарантирует справедливости, напротив, кососимметричные матрицы (когда
HH
T
) соответствуют совершенно справедливой игре, то есть при
оптимальных стратегиях, как это легко установить, цена игры
0V
.
Пример (п.2.2)
Цех заготовитель поставляет в сборочный цех детали двух видов a и b. По
договору между цехами оговорены ежедневно два срока поставки этих деталей,
причём, при поставке в первый срок деталей вида «а» сборочный цех платит
заготовительному премию 50 руб., при поставке же изделий «а» выплачивается
премия 20 руб. При поставке же изделий вида «b» в первый срок премия
составляет 30 руб., а во второй – 40 руб. Определить оптимальные стратегии
поставок и получения деталей.
Решение. Принимая цех-заготовитель за игрока А, а сборочный за В,
составим матрицу игры.
15
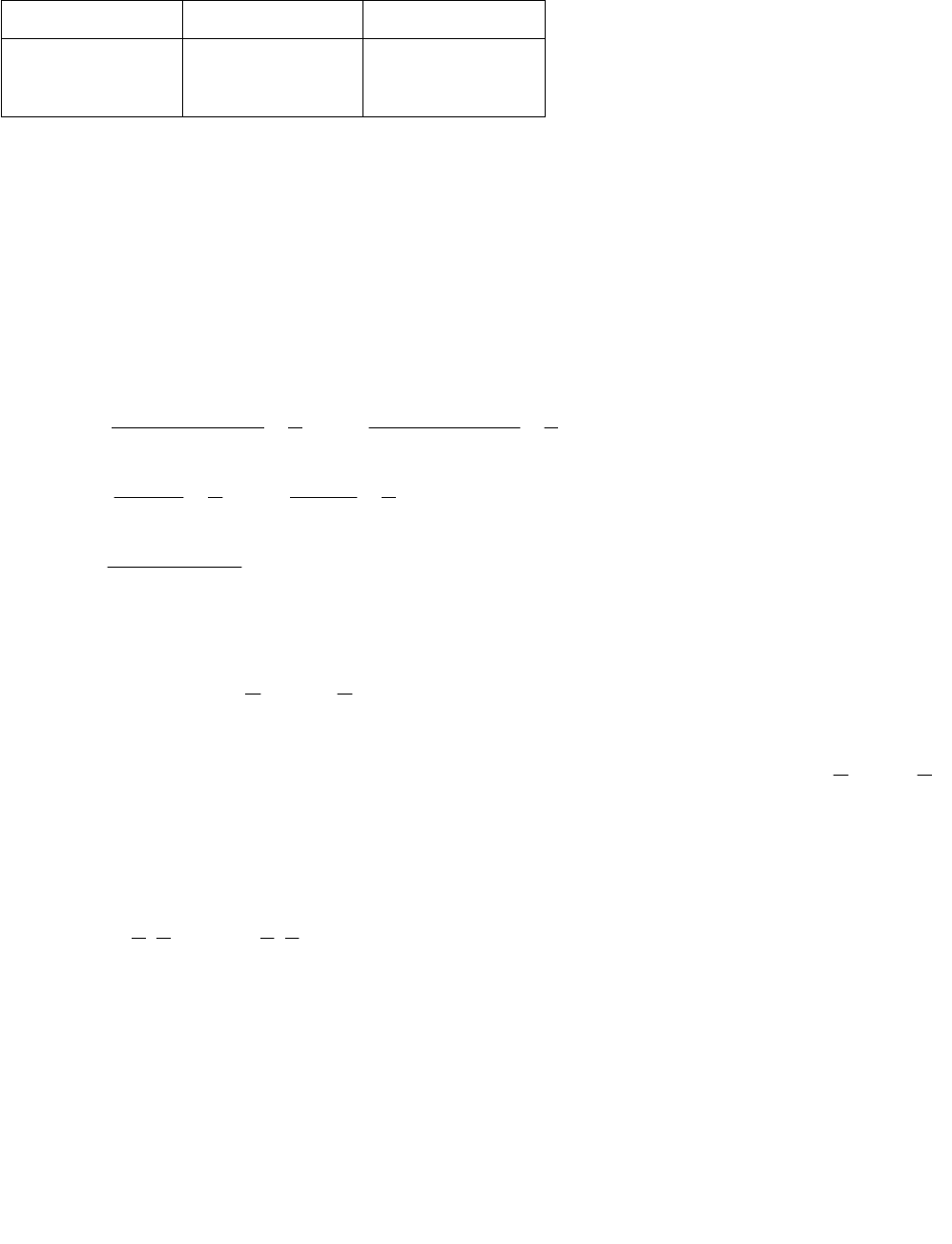
Таблица 2.1
Матрица игры заданная таблицей
I срок II срок
Детали «а»
Детали «b»
50
30
20
40
Значит,
4030
2050
H
,
3030;20maxminmax
ij
j
i
a
,
4040;50minmaxmin
ij
i
j
a
,
, следовательно, седловой точки нет. Для нахождения оптимальных
стратегий применим формулы (2.4), (2.5), (2.6), (2.8) и (2.9):
4
1
30204050
3040
1
x
;
4
3
30204050
2050
2
x
;
2
1
40
2040
1
y
;
2
1
40
3050
2
y
;
35
40
30204050
V
(руб.).
Таким образом, цех-изготовитель поставляет детали вида а и b с
вероятностями
4
1
1
x
,
4
3
2
x
, при этом гарантированная премия 35 рублей, а
сборочный цех получает эти детали в сроки I и II с вероятностями
2
1
1
y
,
2
1
2
y
и
выплачивает 35 рублей премии заготовительному цеху ежедневно. Полученные
вероятности и определяют оптимальные стратегии
4
3
;
4
1
X
,
2
1
;
2
1
Y
.
Примечание. Игры
22
допускают простое графическое толкование и
решение, следующее из него. Действительно, пусть игра задана матрицей (2.1). На
оси абсцисс отложим отрезок 0D, равный 1, и условимся считать, что левый конец
отрезка
1
1
x
– стратегии А
2
, тогда промежуточная точка N с координатой x
соответствует некоторой смешанной стратегии первого игрока, причём,
xx 1
1
,
xx
2
, так как при
0x
имеем
1
1
x
и
0
2
x
, и при
1x
имеем
0
1
x
и
1
2
x
.
16

Вводя ось 0y, можно построить прямую, отвечающую стратегии второго
игрока, её уравнение
xaxay
2111
1
(при каждом x, y даёт значение выигрыша
игрока А, когда В применяет стратегию В
1
). Отметим, что для построения В
1
достаточно провести из концов отрезка 0D прямые, не перпендикулярные ему, на
левой прямой отложить
11
a
, на правой –
21
a
и, соединив их получим прямую
В
1
В
1,
отвечающую стратегии В
1
рис. 2.1. Затем аналогично строим стратегию В
2
(её уравнение
xaxay
2212
1
). Заметим , что при каждом x точки на прямых
В
1
В
1
и В
2
В
2
отвечают выигрышем первого игрока при применении вторым
игроком стратегий В
2
и В
1
соответственно. Откуда следует, что ломаная В
2
КВ
1
рис.
2.2 отвечает нижней границе выигрыша игрока А, а значит в точке её максимума,
то есть цена игры
KNV
и точка N отвечает оптимальной стратегии игрока А:
21
; xxX
xxxx
21
,1
.
Для нахождения оптимальной стратегии игрока В, исходя из графика, можно
воспользоваться формулами:
12
2
1
LBLB
LB
y
; (2.10)
12
1
2
LBLB
LB
y
. (2.11)
В справедливости формул (2.10) и (2.11) легко убедиться, подставив
значения LB
2
и LB
1
,
222
aVLB
,
VaLB
211
и значение
21122211
21122211
aaaa
aaaa
V
, тогда
получим формулы, совпадающие с (2.10) и (2.11).
Аналогично, меняя ролями x и y, можно построить решение для игрока А.
17
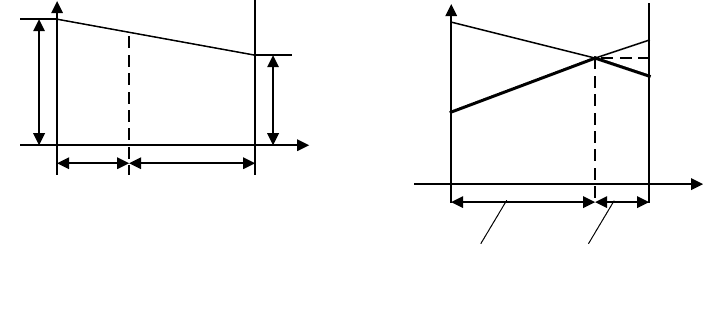
рис. 2.1. Графическое рис. 2.2. Графическое
толкование игры
22
толкование игры
22
18
B
1
N
B
1
a
11
y
x
1
xx
2
y
B
2
(20)
N
K
a
21
x0 xD D0
B
1
(50)
B
1
(30)
B
2
(40)
4
3
2
x
4
1
1
x
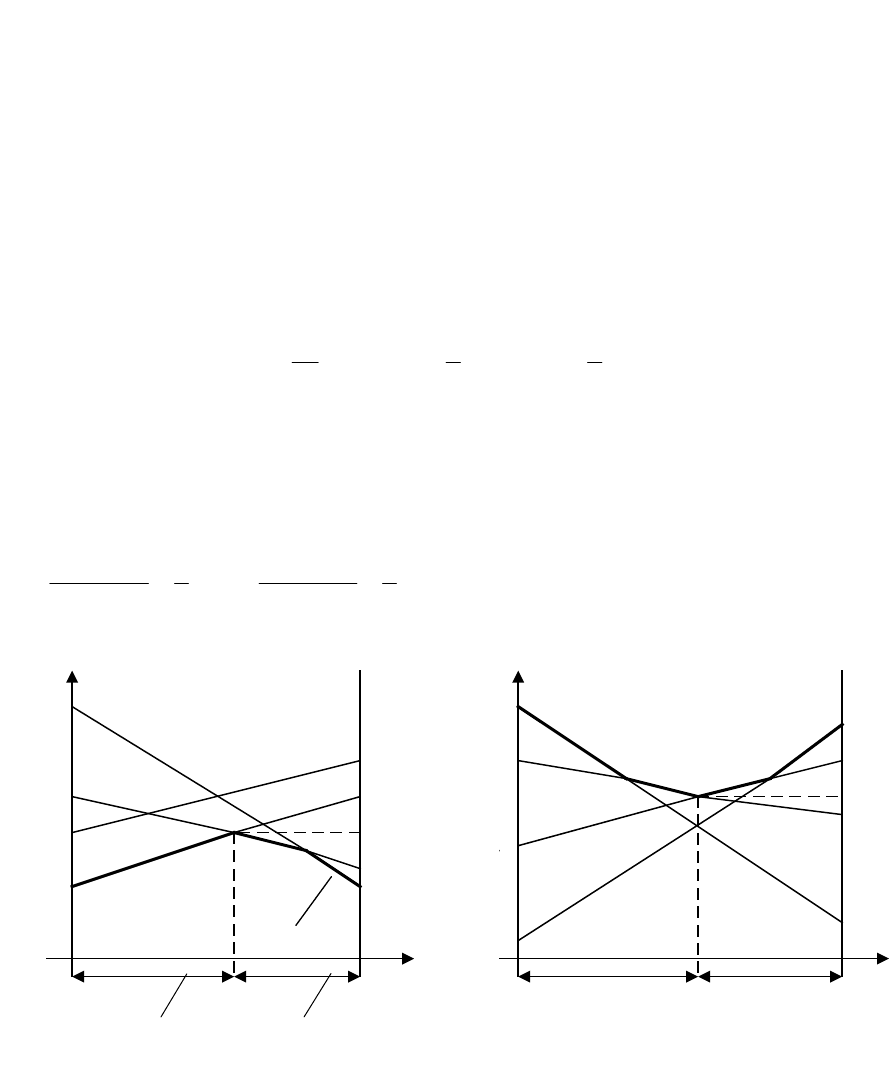
2.2. Решение игры
n2
.
Пусть игра задана матрицей
10569
61284
H
.
Строим прямые, соответствующие стратегиям игрока В рис. 2.3.
Ломаная
31
KMBB
соответствует нижней границе выигрыша, точка К на ней
даёт решение игры:
7
48
KNV
,
7
3
1
NDx
,
7
4
0
2
Nx
.
В данном случае оптимальная стратегия противника получается
применением смеси двух полезных стратегий
1
B
и
2
B
, пересекающихся в точке
К. Стратегия
4
B
является заведомо выгодной при оптимальных стратегиях.
7
2
21
2
1
LBLB
LB
y
,
7
5
21
1
2
LBLB
LB
y
.
рис. 2.3. Иллюстрация рис. 2.4. Иллюстрация
решения игры
n2
решения игры
2m
19
y
x
N
D
B
1
(4)
B
1
(9)
B
2
(6)
B
3
(5)
B
4
(10)
B
4
(6)
B
2
(8)
B
3
(12)
L
7
48
V
K
M
y
x
D
L
N
y
1
y
1
A
4
A
3
A
2
A
1
A
4
A
3
A
2
A
1
K
M
P
7
4
2
x
7
3
1
x
0
0
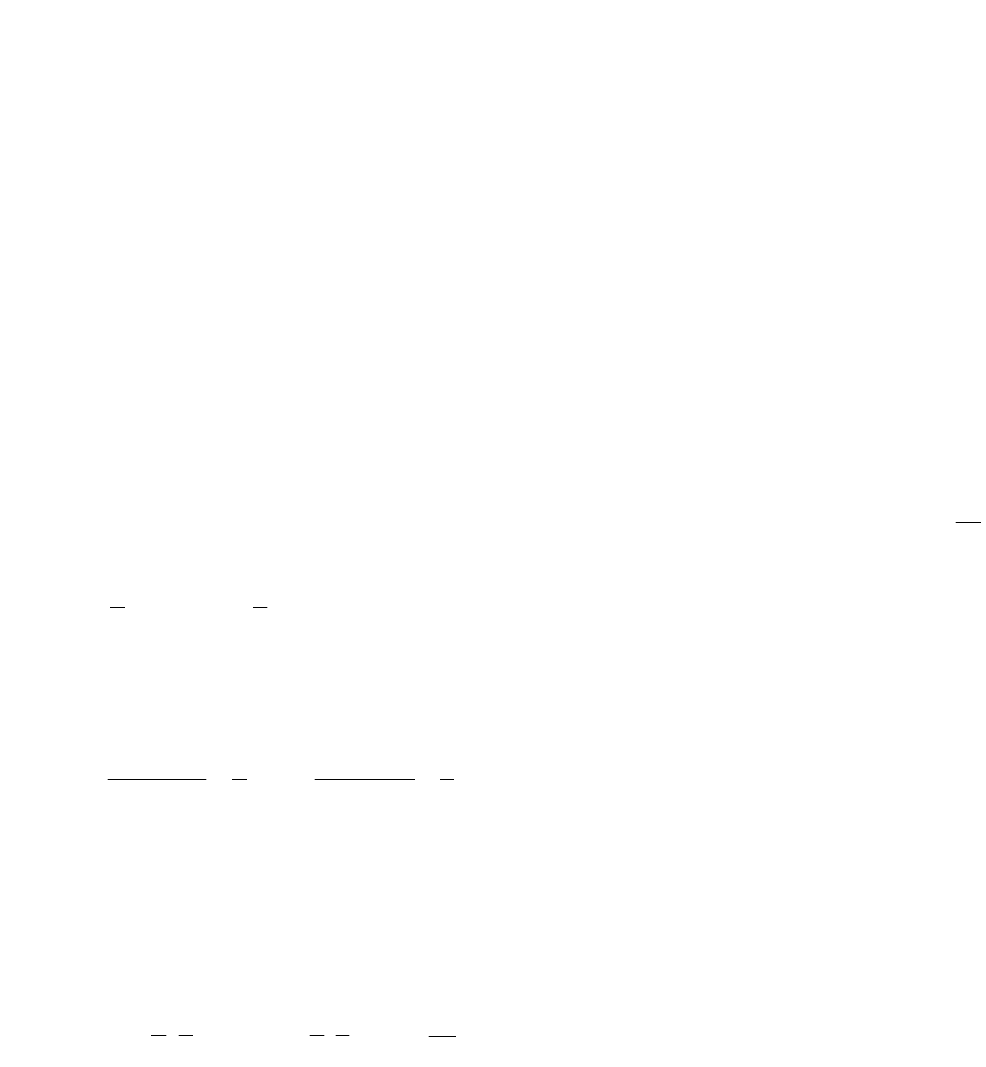
2.3. Решение игры
2m
.
Аналогично может быть решена игра с матрицей
2m
, только в этом случае
строим верхнюю границу выигрыша и на ней определяем минимум.
Пусть игра задана матрицей
111
97
710
212
H
.
Решение задачи находим для игрока В рис. 2.4.
Ломаная
41
PKMAA
изображает верхнюю границу выигрыша игрока А, на ней
ищется точка К с минимальной ординатой, которая и есть цена игры
5
41
KNV
,
5
2
1
NDy
,
5
3
0
2
Ny
.
Оптимальными стратегиями для игрока А являются вторая и третья. При
этом
5
2
32
3
2
LALA
LA
x
,
5
3
32
2
3
LALA
LA
x
.
Матрица оптимальных стратегий имеет вид
97
710
. Тогда решение можно
найти по формулам (2.4), (2.5), (2.6), (2.8) и (2.9).
Следовательно, решение игры таково:
0;
5
3
;
5
2
;0X
,
5
3
;
5
2
Y
,
5
41
V
.
20

2.4. Решение матричных игр
nm
.
При решении произвольной конечной игры размера
nm
рекомендуется
придерживаться следующей схемы:
1. Исключить из платёжной матрицы заведомо невыгодные стратегии по
сравнению с другими стратегиями. Такими стратегиями для игрока А (игрока В)
являются те, которым соответствуют строки (столбцы) с элементами заведомо
меньшими (большими) по сравнению с элементами других строк (столбцов).
2. Определить верхнюю и нижнюю цены игры и проверить, имеет ли игра
седловую точку. Если седловая точка есть, то соответствующие ей стратегии
игроков будут оптимальными, а цена игры совпадает с верхней (нижней) ценой.
3. Если седловая точка отсутствует, то решение следует искать в смешанных
стратегиях. Для игр размера
nm
рекомендуется симплексный метод, а для игр
размером
22
,
m2
,
2m
следует руководствоваться выводами предыдущих
пунктов.
Пример (п.2.3)
Магазин может завести в различных пропорциях товары четырёх типов
4321
,,, AAAA
. Их реализация и прибыль магазина зависят от вида товара и
состояния спроса.
Предполагается, что спрос может иметь пять состояний
54321
,,,, BBBBB
и не
прогнозируется. Определить оптимальные пропорции в закупке товаров из
условия максимизации средней гарантируемой прибыли, при следующей матрице
прибыли табл. 2.2.
Таблица 2.2
Матрица прибыли
Тип
товара
Спрос
В
1
В
2
В
3
В
4
В
5
А
1
А
2
А
3
А
4
200
300
400
700
400
400
500
300
600
600
600
500
400
500
500
200
700
800
800
100
21
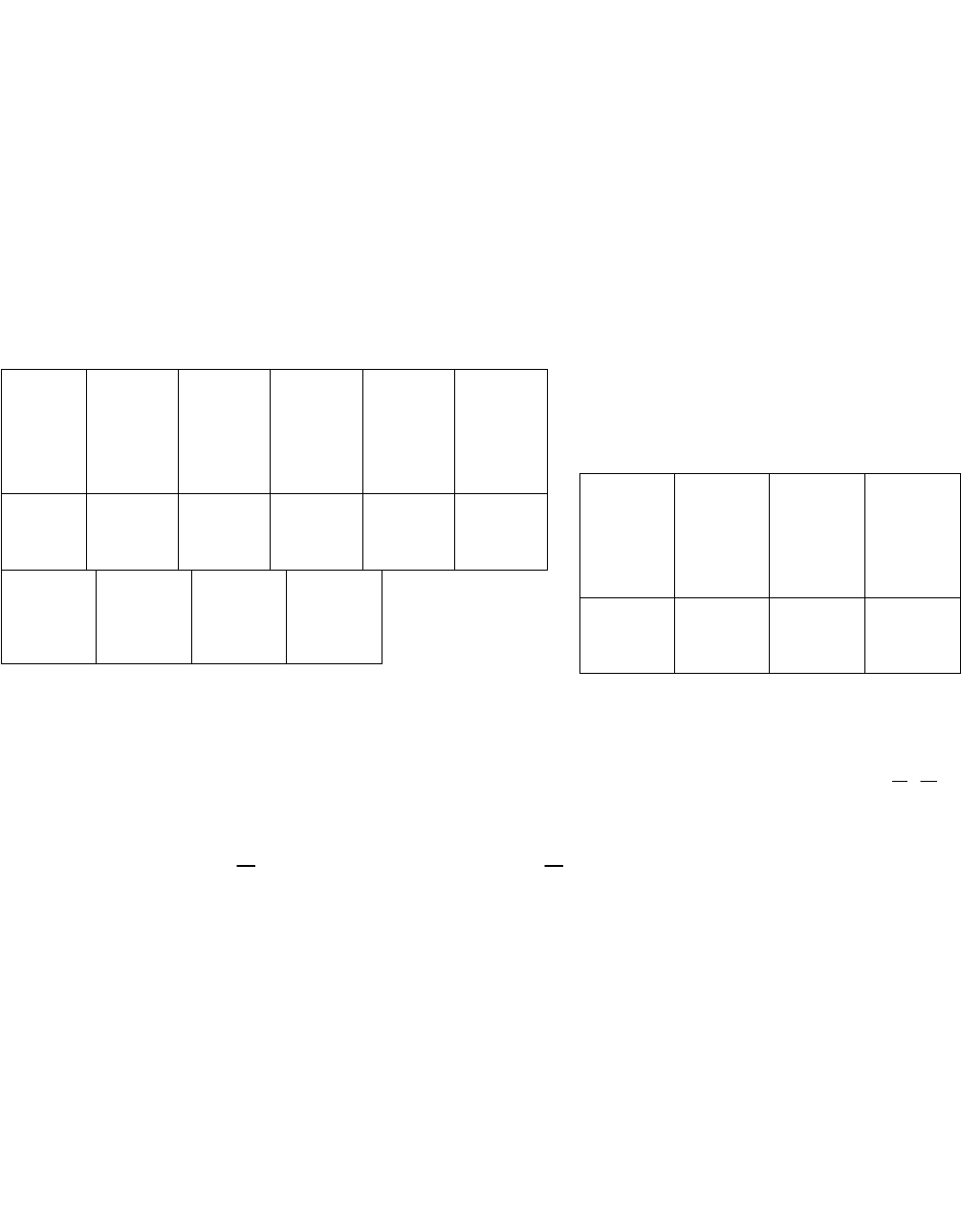
Будем рассматривать возникшую ситуацию как игровую. Сторона А
стремится увеличить прибыль, а потому для неё стратегия
1
A
заведомо выгодна
по сравнению со стратегией
2
A
. Точно так же стратегия
2
A
уступает стратегии
3
A
, и исходные данные упрощаются табл. 2.3.
Для игрока В естественным является выбор стратегии с большим спросом.
Поэтому стратегия
4
B
менее выгодна, чем стратегия
2
B
, в свою очередь,
стратегия
2
B
невыгодна по сравнению со стратегией
3
B
.
Таблица 2.3 Таблица 2.4
Матрица игры заданная таблицей Матрица игры заданная таблицей
В
А
В
1
В
2
В
3
В
4
В
5
А
3
А
4
400
700
500
300
600
500
500
200
800
100
Следовательно, имеет смысл анализировать игру
32
, заданную табл. 1.4.
Решение этой матрицы даёт оптимальную стратегию завоза товаров
5
2
,
5
3
,0,0
,
т.е. нужно завести
5
3
товара третьего типа и
5
2
товара четвёртого типа, а товары
первого и второго типов не завозить, при этом средняя гарантированная прибыль
(цена игры)
520V
.
Пример (п.2.4)
Предполагается оснастить цех новой технологической линией.
Промышленность выпускает три типа линий. На каждой из линий можно
изготовлять пять различных видов изделий. Учитывая расходы сырья,
трудоёмкость, спрос и др., составлена матрица предполагаемой прибыли
1284810
76598
5143102
H
.
22
В
А
В
1
В
3
В
5
А
3
А
4
400
700
600
500
800
100
