Курсовая работа - Оптимизация работы АЗС методами СМО
Подождите немного. Документ загружается.

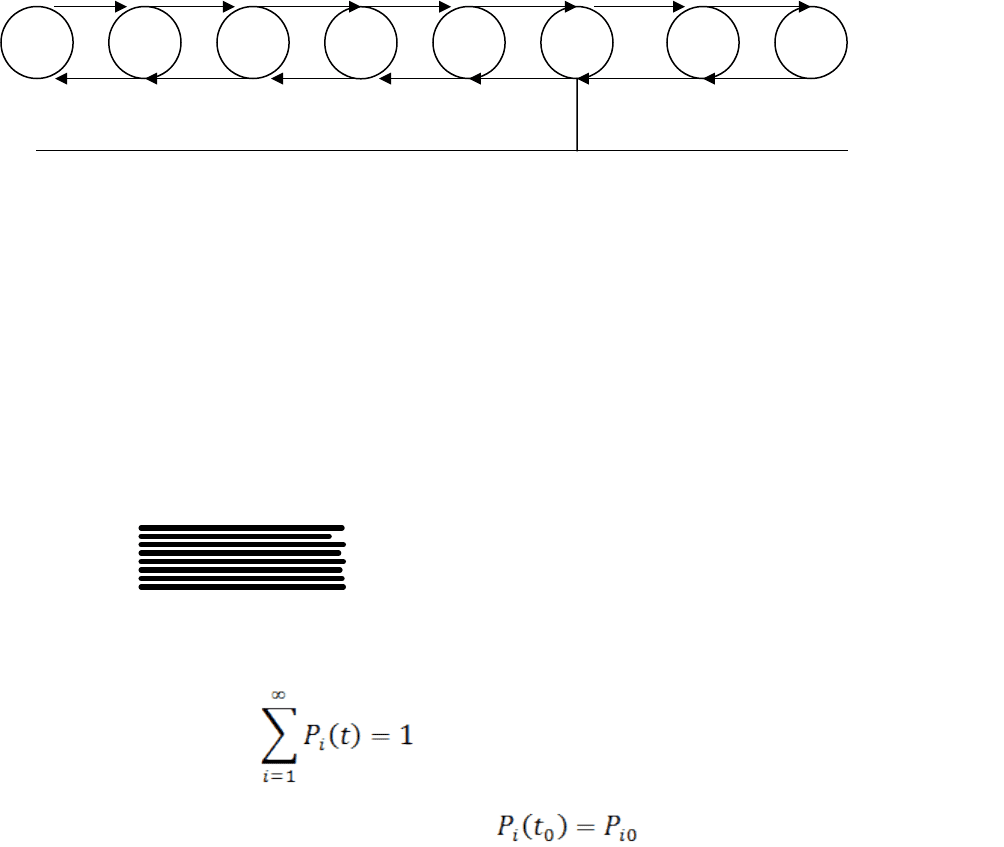
Итак, имеется пятиканальная СМО с ожиданием, в которой число
заявок в очереди не ограничено, а время пребывания в очереди ограничено
m
Tоч
, которое равно 0,1 единиц времени. Тогда плотность ухода заявок,
стоящих в очереди: υ=10.
При анализе случайных процессов с дискретными состояниями и
непрерывным временем удобно пользоваться вариантом схематичного
изображения возможных состояний СМО в виде графа. Рассмотрим граф
состояний описываемой СМО, изображенный на рисунке 1.
Состояния СМО изображены кружками, а возможные направления
переходов из одного состояния в другое ориентированы стрелками,
соединяющими эти состояния.
– это интенсивность входящего потока, а
– это интенсивность обслуживания заявок. Переходы СМО из одного
состояния в другое происходят под воздействием поступления заявок на
заправку и их обслуживание.
Составим уравнение Эрланга для данной системы:
876
7
765
6
654
5
543
4
432
3
321
2
210
1
10
0
)305()205(
;)205()105(
;)105()5(
;5)4(
;4)3(
;3)2(
;2)(
;
PPP
dt
dP
PPP
dt
dP
PPP
dt
dP
PPP
dt
dP
PPP
dt
dP
PPP
dt
dP
PPP
dt
dP
PP
dt
dP
Система дифференциальных уравнений дополняется условием
нормировки
Фиксируются начальные условия
Для построения графика зависимости вероятностей системы от
времени воспользуемся пакетом Mathcad.
Р0 Р1 Р6Р5Р4Р3Р2 Р7
λ
λ
λλ
λ λ λ
μ 2μ 3μ 4μ 5μ+20
5μ+10
5μ
Нет очереди очередь
11
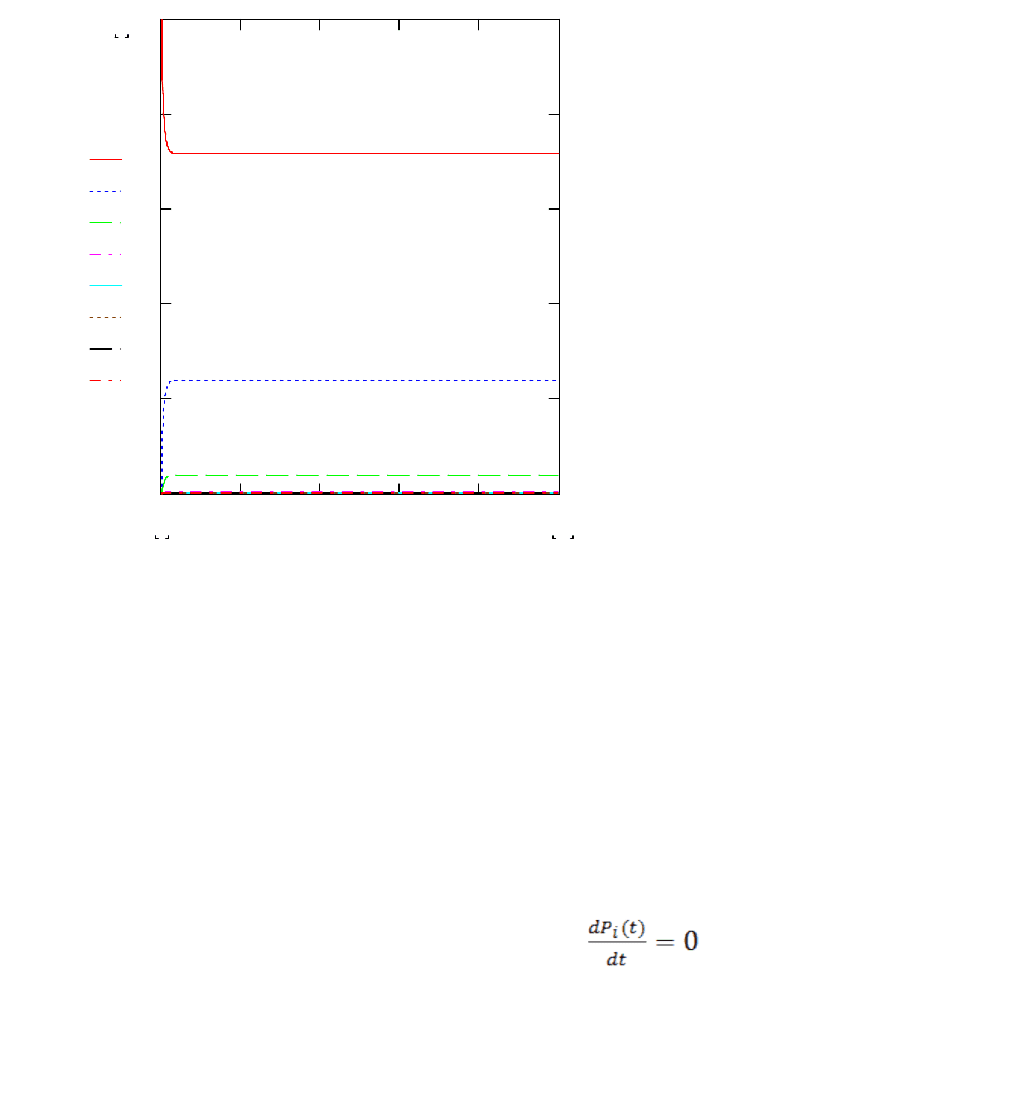
0 2 4 6 8 10
0
0.2
0.4
0.6
0.8
1
0
P0
P1
P2
P3
P4
P5
P6
P7
100 t
Из графиков видно, что система переходит из динамического состояния
в стационарное еще не доходя до t=1.
1) Стационарная система
Поскольку предельные вероятности системы постоянны, то, заменив в
уравнениях Эрланга соответствующие произвольные нулевыми значениями,
получим систему линейных алгебраических уравнений, описывающих
стационарный режим СМО. Такую систему уравнений составляют по графу
состояний СМО. Для стационарной системы . Отсюда получаем
систему линейных уравнений:
876
765
654
543
432
321
210
10
)305()205(0
;)205()105(0
;)105()5(0
;5)4(0
;4)3(0
;3)2(0
;2)(0
;0
PPP
PPP
PPP
PPP
PPP
PPP
PPP
PP
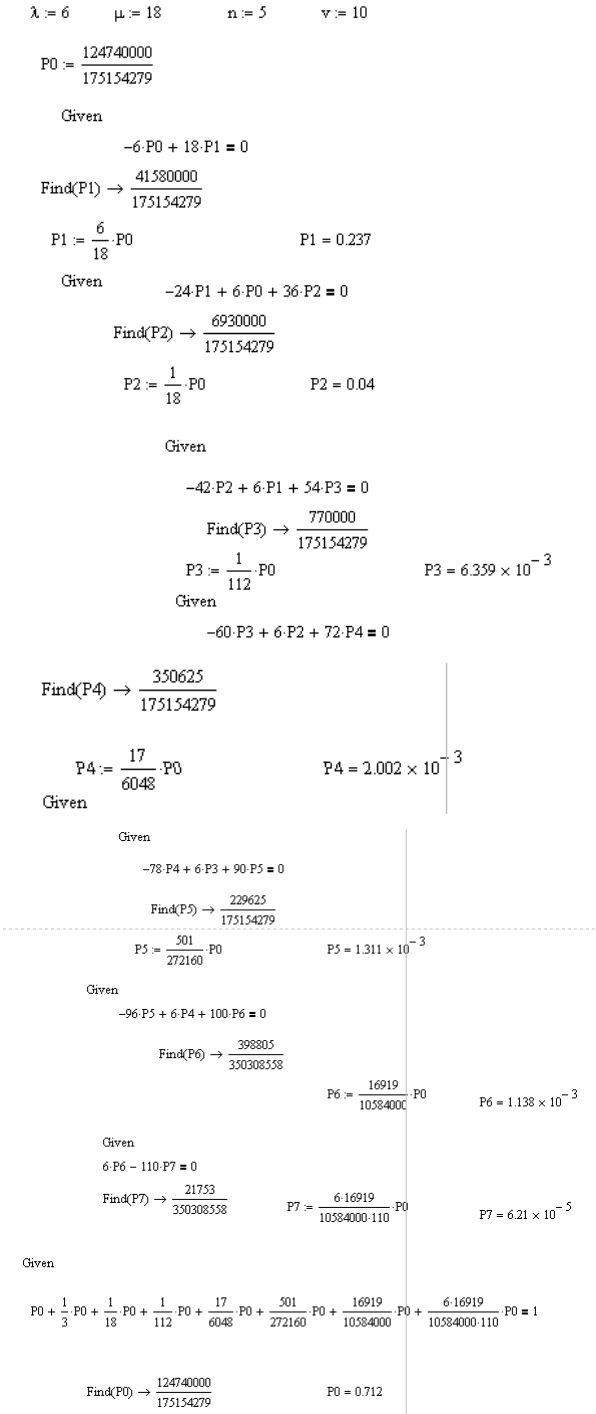
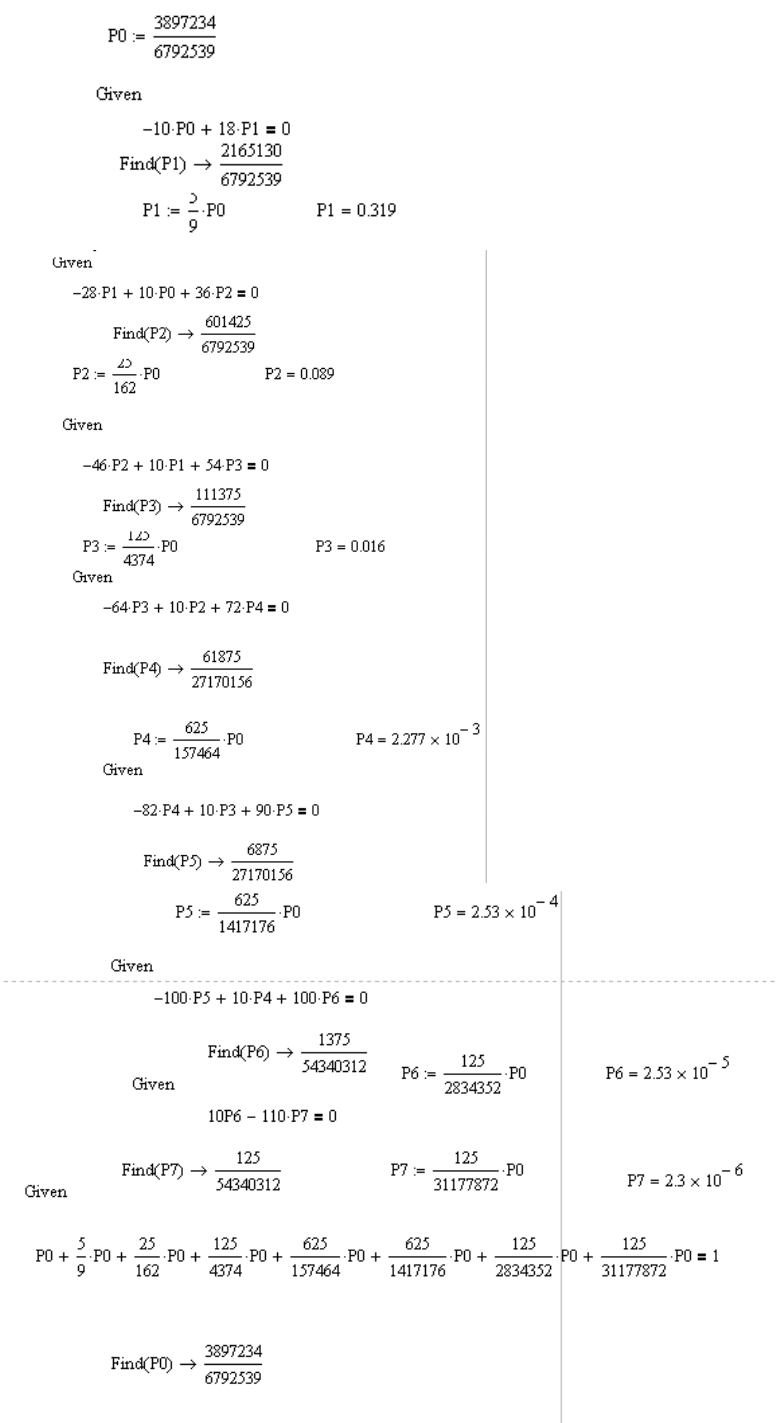
Найдем предельные вероятности состояний, ограничиваясь теми
которые не меньше 0,00001.
Рассчитаем вероятностные характеристики в пакете Mathcad.
12
13

2) Нестационарная система
14

15

16
0 5 10 15 20
0
0.2
0.4
0.6
0.8
1
1.2
1.002
0
p0
p1
p2
p3
p4
p5
p6
p7
160 t
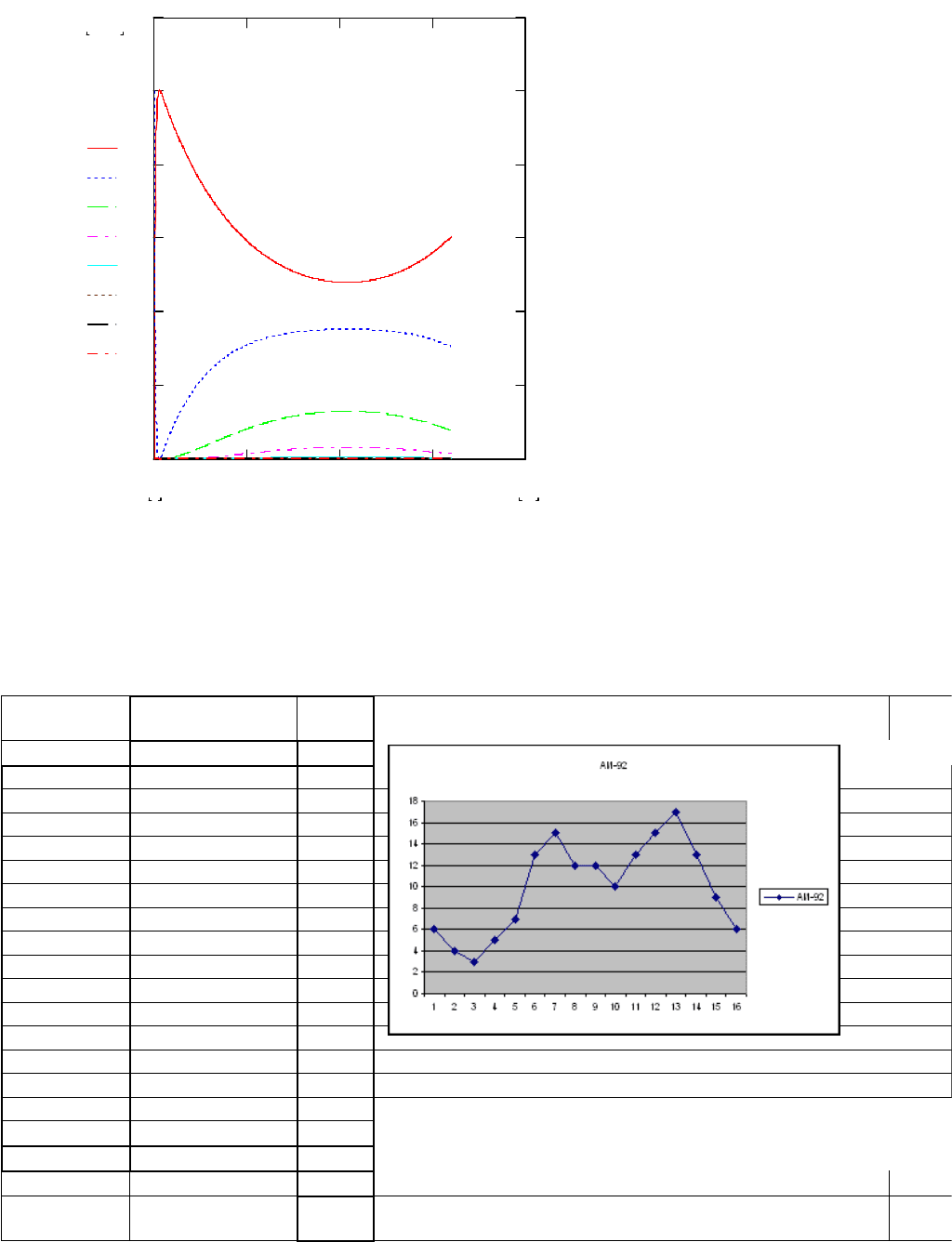
По графику мы можем заметить, что на интервале (6;10) систему
можем рассматривать как стационарную.
2.2. Система АИ-92
Рассмотрим вторую систему: АИ-92
за
ед.времени=1.5ч
период ti yi
00:00-01:30 1 6
01:30-03:00 2 4
03:00-04:30 3 3
04:30-06:00 4 5
06:00-07:30 5 7
07:30-09:00 6 13
09:00-10:30 7 15
10:30-12:00 8 12
12:00-13:30 9 12
13:30-15:00 10 10
15:00-16:30 11 13
16:30-18:00 12 15
18:00-19:30 13 17
19:30-21:00 14 13
21:00-22:30 15 9
22:30-24:00 16 6
136 160
10
машин в ед.времени
18
интенсивность обслуживания одним каналом одной
заявки
λ=10 машин в ед.времени.
n=5 количество каналов
17

m
Tобсл
=5 мин=0,05555(5) ед.времени среднее время обслуживания
заявки µ= =18
Для расчета функции эффективности даны:
qe 380
qp 100
qy 45
qo 500
Итак, имеется пятиканальная СМО с ожиданием, в которой число
заявок в очереди не ограничено, а время пребывания в очереди ограничено
m
Tоч
, которое равно 0,1 единиц времени. Тогда плотность ухода заявок,
стоящих в очереди: υ=10.
Для построения графика зависимости вероятностей системы от
времени воспользуемся пакетом Mathcad
Из графиков видно, что еще не достигая t=1, система переходит из
динамического в стационарный режим
0 2 4 6 8 10
0
0.2
0.4
0.6
0.8
1
0
P0
P1
P2
P3
P4
P5
P6
P7
100 t
Для стационарной системы
Получаем задачу, аналогичную первой, различающуюся лишь в
значениях параметров.
18
19

2) Нестационарная система
20
