Куликовский П.Г. Справочник любителя астрономии

Подождите немного. Документ загружается.

§ 2.6. О погрешностях наблюдений 221

измерений от среднего |ж,- - ж,| = |Д,|, которые часто называют остаточными

уклонениями, т. е.

„ = (39,

Отношение е^/х называется средней относительной погрешностью и может быть

выражено в процентах.

Примечание. Если п невелико, лучше пользоваться более строгой формулой

Е IA.-I

£N =

/ < Л '

(40)

\/п(п - 1)

Окончательный результат определения среднего арифметического значения

можно записать в форме

х ± e

Пример. 10,54 ±0,32 (средняя погрешность).

Часто погрешность среднего арифметического характеризуют величиной средней

квадратической погрешности (по-английски standard deviation) результата, которую

вычисляют по отклонениям Д, каждого измерения от среднего арифметического

по следующей формуле:

_ /А

+ А1 + А1 + ... + А1 /_£Д|_

у n(n -1) -у soTTi)-

(4,)

Средняя погрешность £JV и средняя квадратическая пофешность v

при доста-

точно большом числе п связаны между собой соотношением

елг = J^Cn = 0,7979<7jv, (42)

Характеристикой погрешности среднего результата может служить его вероятная

погрешность а

(по-английски probable error); это такая величина погрешности, при

которой число меньших погрешностей равно числу больших:

= 0,67449сг

ЛГ

и -dff,

<т

= 0,84535елг.

Можно оценить также среднюю квадратическую пофешность отдельного измерения

^ = тЕ

. (

)

либо его вероятную погрешность

= 0,67449s^.

Хотя теория случайных ошибок требует большого числа измерений, ее правила

часто применяют и к небольшому числу измерений, так как и в этом случае они

дают лучшие результаты и приближенное представление о точности измерений.

Если отдельные наблюдения неравноценны по точности — неравноточны, то

при вычислении среднего каждое отдельное значение ж,, полученное из измерений,

222

Глава 2. Некоторые сведения по математике

умножается на вес pi, выраженный в какой-нибудь шкапе (чем точнее измерение,

тем больше его вес), а сумма произведений делится на сумму всех весов

„ = Ц?Р±=х. (45)

ЕР.

Можно оценить относительную погрешность самой средней квадратической

погрешности по формуле

Д«т„ = , (46)

где п — число измерений, вошедших в определение <t

. Таким образом, при четырех

измерениях Аа^ составляет около 35% величины при п = 50 погрешность

в определении стдг составляет примерно 1/10 величины

Среднее арифметическое определяется тем, что, во-первых, сумма отклонений

от него близка к нулю, а во-вторых, сумма квадратов уклонений от него отдельных

измерений должна быть наименьшей. Следовательно, если взять ряд значений

измеряемой величины, близких к предполагаемому наивероятнейшему ее значению,

и составить для каждого значения суммы квадратов уклонений отдельных измерений,

то наименьшая сумма будет соответствовать искомому наивероятнейшему значению

измеряемой величины. На этом свойстве основан разработанный Гауссом способ

наименьших квадратов (§ 2.9).

§2.7. О представлении распределения

гауссовой кривой

Желая получить наиболее вероятное значение какой-либо величины (например,

длины предмета) из многократных ее измерений, или желая оценить общую картину

отклонений отдельных значений какой-либо величины от некоего среднего, либо,

наконец, выяснить картину распределения численностей различных значений одной

какой-либо характеристики как функцию этой характеристики, можно сделать срав-

нение с соответствующей данному случаю кривой нормального распределения (гауссовой

кривой).

Закон нормального распределения можно записать в виде

(47)

где х — наиболее вероятное значение х определяется по положению максимума

кривой Гаусса, а <т — среднее квадратическое отклонение — по положению точек

перегиба этой кривой (рис. 151), а

— дисперсия этого нормального распределения.

Гауссова кривая описывает стандартную картину отклонений измеряемой ве-

личины от среднего — отклонений, происходящих от одних только случайных

погрешностей.

Пусть имеется N значений какой-либо величины х. Возьмем ряд равноотсто-

ящих значений этой величины Х{. Каждому из них будет соответствовать число щ

встречаемости значения ж, в ряду значений х. Очевидно, П\+П2 + П} +..

+ п

— N.

Теперь сравним распределение чисел n; по i с нормальным распределением.

Тогда мы получим наивероятнейшее значение х величины х и характеристику точ-

ности ее определения из наших N измерений. Положение максимума кривой Гаусса

даст наивероятнейшее значение х измеренной величины, а точки перегиба дадут

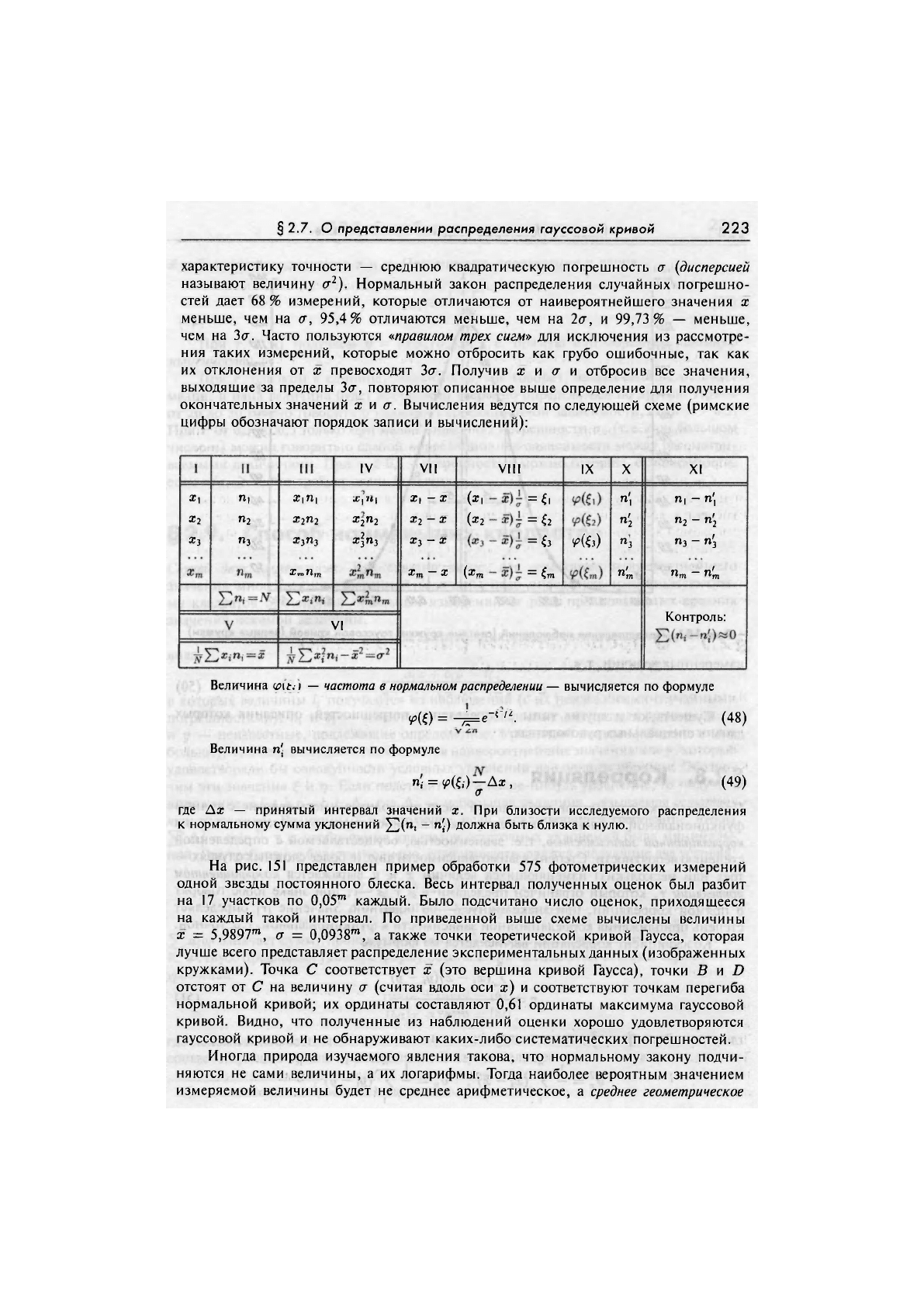
§ 2.7. О представлении распределения гауссовой кривой

223

характеристику точности — среднюю квадратическую погрешность а (дисперсией

называют величину о

). Нормальный закон распределения случайных погрешно-

стей дает 68 % измерений, которые отличаются от наивероятнейшего значения х

меньше, чем на о, 95,4% отличаются меньше, чем на 2а, и 99,73 % — меньше,

чем на 3а. Часто пользуются «правилом трех сигм» для исключения из рассмотре-

ния таких измерений, которые можно отбросить как грубо ошибочные, так как

их отклонения от х превосходят За. Получив х и <т и отбросив все значения,

выходящие за пределы Зет, повторяют описанное выше определение для получения

окончательных значений х и <т. Вычисления ведутся по следующей схеме (римские

цифры обозначают порядок записи и вычислений):

ж,

x-i

п,

Ж|П|

П2

Х]П)

XrnTlin

X] 11\

х]п

VII VIII

IX X XI

Х|

— X

(ж,

=(,

п, - п\

— X

(х

= 6

п'

—

п'

X] -

= 6

vte)

"з

щ - п'з

Хщ х

(Х

=и

П'

«ш - п'

Контроль:

Величина — частота в нормальном распределении — вычисляется по формуле

т = (48)

Величина п\ вычисляется по формуле

n; = v>fe)-A*. (49)

(Т

где Ах — принятый интервал значений х. При близости исследуемого распределения

к нормальному сумма уклонений £(п, - п'

{

) должна быть близка к нулю.

На рис. 151 представлен пример обработки 575 фотометрических измерений

одной звезды постоянного блеска. Весь интервал полученных оценок был разбит

на 17 участков по 0,05™ каждый. Было подсчитано число оценок, приходящееся

на каждый такой интервал. По приведенной выше схеме вычислены величины

х = 5,9897

, о = 0,0938

, а также точки теоретической кривой Гаусса, которая

лучше всего представляет распределение экспериментальных данных (изображенных

кружками). Точка С соответствует х (это вершина кривой Гаусса), точки В и D

отстоят от С на величину <т (считая вдоль оси х) и соответствуют точкам перегиба

нормальной кривой; их ординаты составляют 0,61 ординаты максимума гауссовой

кривой. Видно, что полученные из наблюдений оценки хорошо удовлетворяются

гауссовой кривой и не обнаруживают каких-либо систематических погрешностей.

Иногда природа изучаемого явления такова, что нормальному закону подчи-

няются не сами величины, а их логарифмы. Тогда наиболее вероятным значением

измеряемой величины будет не среднее арифметическое, а среднее геометрическое

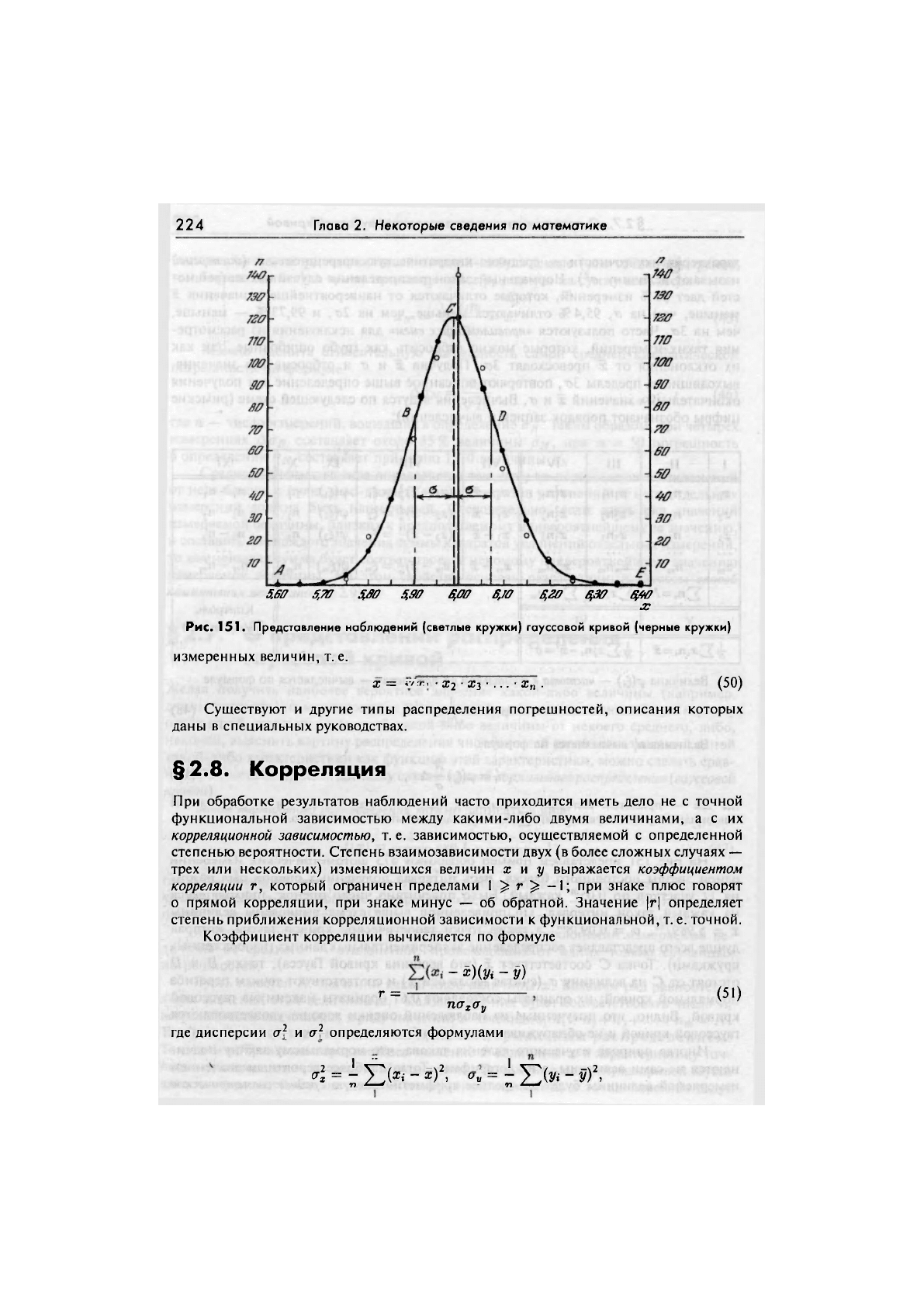
224 Глава 2. Некоторые сведения по математике

Ш 5,70 5,80 5,90 Б,00 В,ГО В,20 $30 $40

Рис. 151. Представление наблюдений (светлые кружки) гауссовой кривой (черные кружки)

измеренных величин, т. е.

X = •

Х2

•

Жз

•...

•

. (50)

Существуют и другие типы распределения погрешностей, описания которых

даны в специальных руководствах.

§2.8. Корреляция

При обработке результатов наблюдений часто приходится иметь дело не с точной

функциональной зависимостью между какими-либо двумя величинами, а с их

корреляционной зависимостью, т. е. зависимостью, осуществляемой с определенной

степенью вероятности. Степень взаимозависимости двух (в более сложных случаях —

трех или нескольких) изменяющихся величин х и у выражается коэффициентом

корреляции г, который ограничен пределами 1 ^ г > -1; при знаке плюс говорят

о прямой корреляции, при знаке минус — об обратной. Значение |г| определяет

степень приближения корреляционной зависимости к функциональной, т. е. точной.

Коэффициент корреляции вычисляется по формуле

- x)(Vi ~ У)

г =

псг

(Т

(51)

где дисперсии сг

и а

определяются формулами

<г

= ^ - х)

, = ^ Y^iVi - V)

§ 2.9. Способ наименьших квадратов

225

х и у — средние значения х и у. Погрешность определения г равна

1 - г

От = —]=-

•

(52)

у/п

При г = ±1 получаем у = (±а

/а

)х, т.е. прямую или обратную линейную

зависимость.

При г, близком к единице, зависимость, как говорят, весьма тесная\ сг

будет

малой, и одна величина будет достаточно уверенно определяться по другой. При га

от 20 до 30 можно говорить о наличии корреляционной зависимости, если г > 0,5.

При г от 0,3 до 0,5 только при малых значениях погрешности а

(т.е. при большом

числе га) можно говорить о слабой корреляционной зависимости между рассматри-

ваемыми величинами. При г < 0,1 с уверенностью можно говорить о зависимости,

если г/(т

^ 4, что требует очень больших га.

§2.9. Способ наименьших квадратов

Случай двух неизвестных. Как сказано выше, для отыскания наивероятнейшего

значения многократно измеренной величины надо определить наименьшую сум-

му квадратов отклонений отдельных измерений от ряда предполагаемых средних

значений искомой величины.

Условными уравнениями способа наименьших квадратов называются уравнения

вида

atx + b

y = l

{

в которых величины получаются из наблюдений (с их неизбежными случайными

погрешностями), а, и Ь, — известные числа, различные для разных уравнений, х

и у — неизвестные, подлежащие определению. Уравнений больше (обычно много

больше), чем неизвестных. Отыскиваются наивероятнейшиезначения х и у, которые

удовлетворяли бы совокупности условных уравнений наилучшим образом. Обозна-

чим эти значения ( и i). Если подставить их в какое-нибудь уравнение, то получим

выражение + bit]

— Z*

= где Д, — небольшая величина, называемая остаточ-

ным уклонением. Величины £ и г] получим, если удовлетворяется требование, чтобы

£ Д,

= min т.е. чтобы сумма квадратов остаточных уклонений была минималь-

ной. Это требование будет выполнено, если удовлетворяются следующие два условия:

£ £ а? + V 12 <4

i ~ Е

i =

Е «А + ri Е ь.

- Е Vi - о.

>bi означает сумму произведений а,Ь,, £ — сумму произведений и т.д.

К. Ф. Гаусс предложил удобную форму обозначений членов этой системы нормальных

уравнений:

[аа]ж + \ab\y = [а/],

[Ьа]х +

[ЪЬ]у

= [Ы],

где искомые неизвестные вновь обозначены х и у, а квадратные скобки обозначают

соответствующие суммы произведений. В случае большего числа неизвестных число

' Это так называемый принцип Лежандра.

226 Глава 2. Некоторые сведения по математике

нормальных уравнений будет равно числу неизвестных. Система нормальных урав-

нений решается способом последовательного исключения по следующей

схеме. Из первого уравнения, деля все его члены на [аа], получают

^ И И ,„v

+ г—\У = ]—т- (53)

[аа] [аа]

Это — первое уравнение исключения. Умножают это уравнение на [аЬ] и вычитают

его из второго нормального уравнения:

[Ъа]х + [ЬЬ]у = [Ы],

[

Ьа]х

[Ьа][аЬ]

у =

[&а|И

[аа] [аа]

Получают второе уравнения исключения с одним неизвестным у. В обозначениях

Гаусса оно записывается так:

[»!]» = [W1],

где

Отсюда

, , , , [яЬ]

, г , \ab][al]

[аа] [аа]

[Ы\] ,

у=

т-

(54)

Полученное у подставляют в первое уравнение исключения, чтобы опреде-

лить х. Задача определения наивероятнейших значений неизвестных х w у решена.

Веса неизвестных х и у равны:

г Льъ\] , ,

= Ру = [ЪЪ 1] • (55)

Средние погрешности неизвестных равны:

= , £у = — , (56)

VP:г s/Py

где

[рАД]

\ Т" •

у п - 2

Подробное изложение теории случайных погрешностей и способа наименьших

квадратов для большого числа неизвестных см. в ПЧАК (гл. 6) либо в книге

Б. М. Щиголева «Математическая обработка наблюдений».

Глава 3

КРАТКИЕ СВЕДЕНИЯ ИЗ ОБЩЕЙ АСТРОНОМИИ

§3.1. Астрономические координаты

Не имея возможности при непосредственных наблюдениях оценивать различие в рас-

стояниях до небесных светил, мы относим их на одно расстояние — на внутрен-

нюю поверхность некоторой сферы, окружающей

наблюдателя, находящегося в ее центре. Небесная

сфера — это воображаемая сфера произвольно-

го радиуса (рис. 152), которая позволяет заменить

изучение взаимного расположения направлений

на светила изучением взаимного расположения то-

чек на сфере.

Чистое небо представляется нам в виде купола

над нашей головой, или небосвода. Кажущаяся

форма небосвода зависит от окружающей обстанов-

ки. В открытой местности купол неба представля-

ется нам сплюснутым — ближе над головой, чем

в горизонте; для наблюдателя, стоящего поблизости

от высоких предметов, небосвод кажется уходящим

дальше в высоту, чем к горизонту.

Вопрос о кажущейся форме небосвода имеет

значение при глазомерных оценках высот светил над

горизонтом в открытой местности, так как в силу

сплюснутости небосвода мы всегда переоцениваем

высоты светил. Различие истинной и кажущейся

высот h объектов над горизонтом:

Истинная h 15° 30° 45° 60° 75°

90°

Кажущаяся h

30°

50°

65° 75°

84° 90°

(См. раздел «Суждение о форме и движении» в очень интересной книге М. Мин-

нарта «Свет и цвет в природе». М.: Наука, 1969.) Степень сплюснутости зависит

от состояния неба и от условий погоды.

3.1.1. Системы координат

Положение точки на сфере определяется в какой-нибудь системе сферических коорди-

нат: горизонтальной, экваториальной, эклиптической или галактической. Расстояния

между точками на сфере измеряются центральными углами или соответственными

дугами больших кругов.

Отвесная линия пересекает сферу в точках зенита и надира (рис. 153). Большие

круги, проходящие через точки зенита и надира, называются вертикальными кругами.

/ /

/ 1

/ /

/ 1

г" К

N--—

190

\ 1

\ \

Ч \

Рис. 152. Условное изображе-

ние небесной сферы (условное

потому, что при таком поло-

жении смотрящего относительно

основной плоскости полюс не мо-

жет совпадать с точкой Р, а бу-

дет находиться на обращенной

к читателю полусфере, пример-

но в точке, отмеченной крестом)

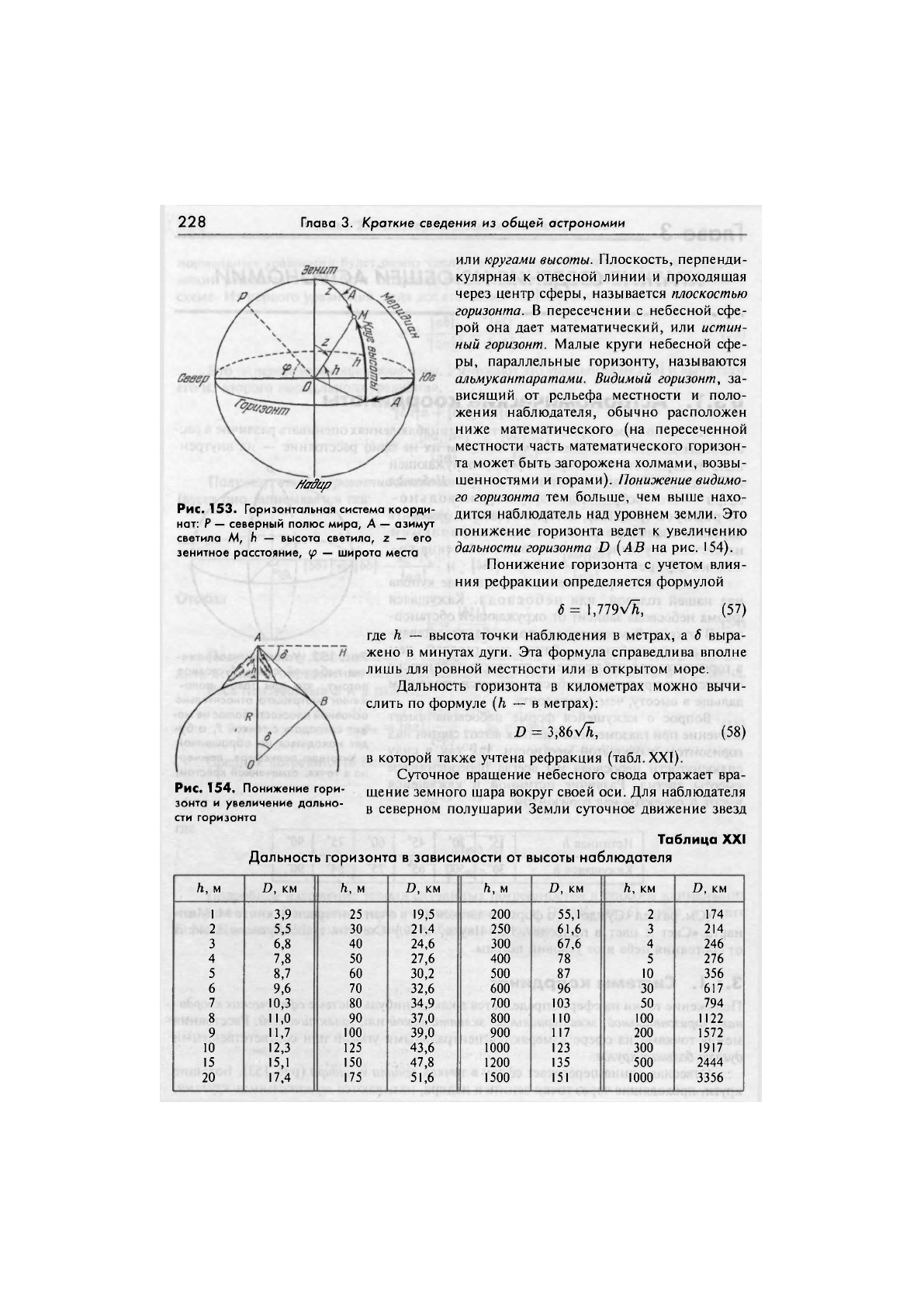
228 Глава 3. Краткие сведения из общей астрономии

//adup

Рис. 153. Горизонтальная система коорди-

нат: Р — северный полюс мира, А — азимут

светила М, h — высота светила, z — его

зенитное расстояние, ip — широта места

или кругами высоты. Плоскость, перпенди-

кулярная к отвесной линии и проходящая

через центр сферы, называется плоскостью

горизонта. В пересечении с небесной сфе-

рой она дает математический, или истин-

ный горизонт. Малые круги небесной сфе-

ры, параллельные горизонту, называются

альмукантаратами. Видимый горизонт, за-

висящий от рельефа местности и поло-

жения наблюдателя, обычно расположен

ниже математического (на пересеченной

местности часть математического горизон-

та может быть загорожена холмами, возвы-

шенностями и горами). Понижение видимо-

го горизонта тем больше, чем выше нахо-

дится наблюдатель над уровнем земли. Это

понижение горизонта ведет к увеличению

дальности горизонта D (АВ на рис. 154).

Понижение горизонта с учетом влия-

ния рефракции определяется формулой

6 = 1,779у/К, (57)

где h — высота точки наблюдения в метрах, а 6 выра-

жено в минутах дуги. Эта формула справедлива вполне

лишь для ровной местности или в открытом море.

Дальность горизонта в километрах можно вычи-

слить по формуле (h — в метрах):

D = 3,86 у/К, (58)

Рис.154. Понижение гори-

зонта и увеличение дально-

сти горизонта

в которой также учтена рефракция (табл. XXI).

Суточное вращение небесного свода отражает вра-

щение земного шара вокруг своей оси. Для наблюдателя

в северном полушарии Земли суточное движение звезд

Таблица XXI

Дальность горизонта в зависимости от высоты наблюдателя

ft, м

D, км

ft, м

D, км

ft, м D, км ft, км

D, км

3,9

25 19,5 200 55,1 2

174

2 5,5 30 21,4 250 61,6

214

3 6,8 40 24,6 300 67,6

246

4 7,8 50 27,6 400 78 5 276

8,7

60 30,2 500

10 356

б 9,6 70 32,6 600 96 30

617

10,3 80

34,9

700 103 50

794

11,0

90 37,0

800 110

100

1122

11,7

100 39,0 900 117 200 1572

12,3 125

43,6

1000 123 300

1917

15,1

150 47,8 1200 135

500 2444

17,4

175

51,6

1500 151

1000 3356

§3.1. Астрономические координаты

23 7

Рис. 155. Движение северного полюса мира с

600 по 2300 гг.

Сетка экваториальных координат эпохи 1950,0

происходит «против часовой стрелки» вокруг

одной точки неба, остающейся неподвиж-

ной. Это — северный полюс мира. На южном

небе это будет южный полюс мира, а движе-

ние звезд происходит «по часовой стрелке».

С течением времени положение полюса

среди звезд медленно меняется вследствие

прецессии. В настоящее время полюс мира

приближается к Полярной звезде (a UMi).

Ближе всего к полюсу a UMi будет около

2110 г. (рис. 155).

Высота полюса мира над горизонтом

равна географической широте у места. Через

центр сферы и полюсы проходит вообра-

жаемая ось вращения небесной сферы (ось

мира), параллельная оси вращения земного

шара. Плоскость, перпендикулярная к оси

мира, образует в пересечении с небесной

сферой большой круг, называемый небесным

экватором (рис. 156). Он отделяет северное

полушарие неба от южного. Малые круги

Зешт

широта места наблюдения, а — прямое

восхождение светила М, 6 — его склоне-

ние, t — часовой угол светила, Т — точка

весеннего равноденствия

230 Глава 3. Краткие сведения из общей астрономии

небесной сферы, параллельные небесному экватору, называются небесными па-

раллелями. Большие полукруги, перпендикулярные к экватору и пересекающиеся

в полюсах мира, называются кругами склонений, или часовыми кругами.

Вертикальная плоскость, проходящая через полюс и зенит, пересекается с не-

бесной сферой по большому кругу, называемому меридианом (от латинского слова

meridies — полдень). Чтобы определить точно положение плоскости меридиа-

на (рис. 157) и ее проекцию на плоскость горизонта — полуденную линию, надо

i им;

- \

UMa/ >

л ' .' Р

6 ' / '

£ ^

А '

; UMi

(

Cas

•

ч У 1

ч Р

\ /

Рис. 157. К определению положения плоскости меридиана (рядом с а UMi

крестиком отмечено положение северного полюса мира в нашу эпоху)

иметь эфемериду (т.е. предвычисленные положения) Полярной в ее движении

вокруг полюса, позволяющую в наблюдательно найденный азимут относительно

неподвижного ориентира на местности внести поправку, учитывающую элонгацию

Полярной в момент наблюдения. В переменной части Астрономического Календаря

для определения широты места по измерениям высоты h Полярной приводятся

таблицы поправок за звездное время, за рефракцию, за азимут Полярной. Имея

в своем распоряжении угломерный инструмент (типа геодезического теодолита),

можно надеяться определить широту с погрешностью ±0,2', если звездное время

момента наблюдения известно с погрешностью не более одной минуты.

Вертикальная плоскость, перпендикулярная к плоскости меридиана, называется

плоскостью первого вертикала. Плоскости меридиана и горизонта пересекаются

по полуденной линии: меридиан с горизонтом пересекается в точках севера N и юга S,

а первый вертикал — в точках востока Е и запада W (рис. 158). Эти четыре точки

горизонта определяют страны света.

В горизонтальной системе координат (рис. 153) положение светила опре-

деляется его высотой h — дугой круга высоты между горизонтом и светилом —

и азимутом А — дугой горизонта от точки юга до точки пересечения круга высоты

с горизонтом (или соответствующим углом при зените между меридианом и кругом

высоты). Азимут отсчитывается от точки юга к западу от 0 до 360°; таким образом,

азимут точки запада равен 90°, точки востока 270°. Иногда определяют западный