Кулешова Е.О., Колчанова В.А., Эськов В.Д., Пустынников С.В. Теоретические основы электротехники в экспериментах и упражнениях
Подождите немного. Документ загружается.


61
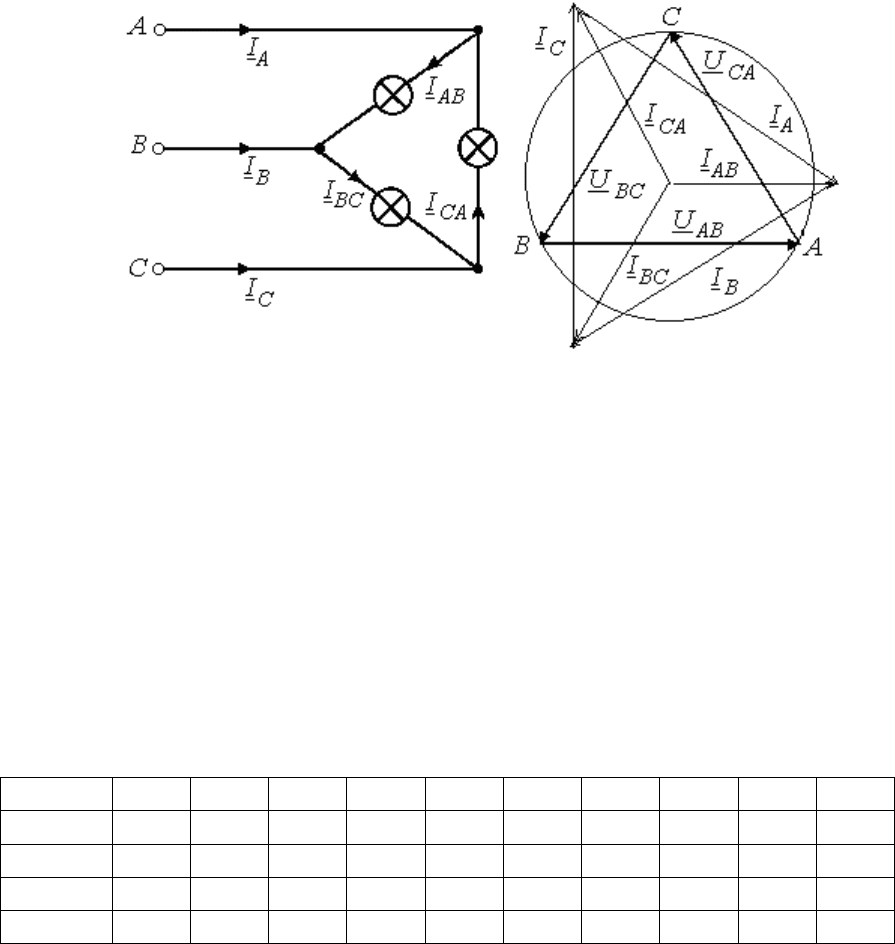
Рис. 10.1
Вольтметр V измеряет линейное напряжение, амперметры А
А
, А
В
,
А
С
– линейные токи, остальные – фазные токи. В качестве ваттметров
используются приборы W
1
и W
2
, к выходным зажимам которых под-
ключены вольтметры, чьи показания в вольтах численно равны показа-
ниям ваттметров в ваттах. Сумма показаний этих приборов равна ак-
тивной мощности цепи.
Подготовка к работе
Проработав материал, ответить на вопросы.
1.
Что такое линейные и фазные токи? Какие уравнения связыва-
ют линейные и фазные токи а) несимметричной и б) симметричной це-
пи, соединенной треугольником.
2.
На каком принципе основано действие индукционного фазо-
указателя? Как с его помощью определить порядок чередования фаз.
3.
Исходная диаграмма напряжений и токов для симметричного
треугольника дана на рис. 10.2:
а) как деформируется диаграмма токов в случае обрыва фазы АВ?
б) во что «выродится» диаграмма токов при обрыве линейного про-
вода А?
Изобразить качественные диаграммы токов для случаев а) и б).
62
а б
Рис. 10.2
Программа работы
1.
Открыть файл LW10 и извлечь из поля вспомогательных ком-
понентов
Favorites две подсхемы (Subcircuit) Wattmeter (на рис. 10.1 –
W
1
и W
2
). Собрать остальную часть схемы, показанной на рис. 10.1, и
установить ее параметры согласно табл. 10.1 в соответствии со своим
вариантом схемы.
Таблица 10.1
№ 1 2 3 4 5 6 7 8 9 10
E (В) 380 220 127 380 220 127 380 220 127 380
R(Ом) 200 150 100 250 200 150 300 250 200 150
L(мГн) 0,64 0,48 0,32 0,8 0,64 0,48 0,95 0,8 0,64 0,48
C(мкФ) 16 21,2 31,8 12,7 16 21,2 10,6 12,7 16 21,2
2.
Снять показания приборов в симметричном режиме (замкнуты
ключи К
1
, К
2
, разомкнуты К
3
, К
4
) и подсчитать отношение I
Л
/I
Ф
. Вычис-
лить также активную мощность P = 3U
Ф
I
Ф
(cosϕ=1 для активной нагруз-
ки).
3.
Исследовать несимметричную цепь в следующих режимах:
а) уменьшение активной нагрузки в фазе АВ, для чего сопротивле-
ние в этой фазе следует увеличить вдвое по сравнению с его табличным
значением

63
б) увеличение активной нагрузки в фазе АВ, для чего сопротивле-
ние в этой фазе следует уменьшить вдвое по сравнению с его таблич-
ным значением;
в) отключение нагрузки в фазе АВ, для чего нужно разомкнуть
ключи К
2
, К
3
, К
4
;
г) включение индуктивности в фазу АВ, для чего необходимо при
замкнутых ключах К
1
, К
3
, разомкнуть ключи К
2
, К
4
;
д) включение емкости в фазу АВ (при замкнутых ключах К
1
, К
4
, ра-
зомкнуть ключи К
2
, К
3
,);
е) обрыв линейного провода А, для чего следует разомкнуть ключ
К
1
при одинаковых активных сопротивлениях нагрузки всех трех фаз;
Результаты всех измерений (пп. 2, 3) внести в табл. 10.2. Туда же
внести значения активной мощности цепи, подсчитанной как по закону
Джоуля-Ленца (
2
PIR=
∑
), так и суммированием показаний ваттметров
(P= P
1
+P
2
).
4.
Построить топографические диаграммы напряжений, совме-
щенных с лучевыми диаграммами токов для всех режимов.
Указание. Всего 5 диаграмм, построение каждой из которых следу-
ет начинать с неизменного для всех диаграмм равностороннего тре-
угольника линейных напряжений. Лучевые диаграммы фазных токов
удобно строить из центра тяжести этого треугольника. Если соединить
концы векторов фазных токов,
то должен получиться треугольник ли-
нейных токов (например, I
A
= I
AB
– I
CA
).
5.
Проанализировать диаграммы и сформулировать выводы по
работе.
Таблица 10.2
I
А
I
В
I
С
I
АВ
I
ВС
I
СА
Р
1
Р
2
Р
ОП
Р
РАСЧ
Характер
нагрузки в фа-
зе АВ
А А А А А А Вт Вт Вт Вт
Симметричная
а)
. . .
е)
64
РАБОТА 11
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С ИСТОЧНИКОМ
НЕСИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ
Цель работы. Изучение влияния катушки индуктивности и кон-
денсатора на форму кривой тока при питании цепи от источника перио-
дического несинусоидального напряжения.
Пояснения к работе
Если к цепи приложено несинусоидальное напряжение, то форма
кривой тока будет подобна форме кривой напряжения лишь в том слу-
чае, когда сопротивление цепи чисто активное. Если же в цепь включе-
на катушка индуктивности или конденсатор, то форма кривой тока от-
личается от формы кривой напряжения.
При последовательном соединении индуктивности L и
сопротивле-
ния R полное сопротивление цепи току k-й гармоники равно
()
2
2
k
ZRkL=+ω. Следовательно, по мере увеличения порядка k гар-
моники это сопротивление увеличивается, амплитуда тока
k-й гармони-
ки уменьшается (по сравнению с чисто активной цепью, имеющей то же
самое сопротивление
R), и кривая тока будет меньше искажена, чем
кривая напряжения.
Если же последовательно включены сопротивление
R и емкость С,
то полное сопротивление такой цепи току
k-й гармоники равно
2
2
1
k
ZR
kC
⎛⎞
=+
⎜⎟
ω
⎝⎠
. Значит, с увеличением порядка k гармоники это
сопротивление уменьшается, амплитуда тока соответствующей гармо-
ники увеличивается, и кривая тока искажается сильнее (по сравнению с
синусоидой), чем кривая приложенного к цепи напряжения.
Схема электрической цепи
Рис 11.1

о
с
ж
э
р
в
с
ч
м
п
и
с
н
д
н
(
к
с
о
т
с
т
а
же
э
к
р
р
а
з
в
у
ю
с
и
м
ч
а
с
ме
п
р
я
и
з
м
с
т
о
ны
д
у
ю
ни
(
р
и
к
а
ж
с
и
м
и
а
в
л
е
н
и
р
а
н
з
о
м
ю
мо
с
т
о
е
тр
яж
м
е
о
р
о
ы
х
т
ющ
и
е
т
и
с.
же
мм
Э
л
и
ст
л
е
н
и
е
н
е
м
к
то
о
с
т
О
т
1.
о
т
ы
2.
а
м
3.
ж
е
н
н
я
ом
а
)
б
)
4.
т
о
к
5.
щи
а
)
б
)
в
)
г
)
6.
т
о
к
7.
1
1
е
н
н
8.
м
е
т
л
е
к
оч
н
н
о
с
о
с
н
у
ка
т
и
о
т
в
е
ы
?
м
и
R
н
и
я
я
ет
с
м
:
)
и
н
)
е
м
к
а
и
х
с
)
э
л
)
э
л
)
м
)
м
к
а
и
1
.
1
н
о
й
т
р
и
к
т
р
н
и
о
г
о
со
п
с
ц
и
у
т
о
в
о
т
е
т
и
R
и
я
.
с
я
н
д
мк
и
н
с
и
с
л
е
к
л
е
к
м
аг
н
аг
н
и
н
1
)
в
й
?
и
ч
н
р
и
ч
и
к
а
о
п
пр
и
л
л
о
м
ц
е
п
о
и
т
ь
К
а
Че
и
L
Р
е
О
т
ф
о
у
к
к
ос
К
а
н
а
К
а
с
т
е
к
т
р
к
т
р
ни
н
и
т
К
а
н
а
п
П
в
ц
К
а
н
о
й
ч
е
с
а
н
п
о
д
р
о
т
л
о
г
ж
е
е
п
и
о
л
о
ь
н
а
а
к
ем
L
в
е
з
и
т
л
и
о
р
м
к
т
и
т
и
а
к
п
р
а
к
и
е
м
р
о
м
р
о
д
и
то
т
о
э
а
к
и
п
р
я
П
о
ч
ц
е
а
к
и
й
о
с
к
а
н
е
с
д
с
х
т
и
в
г
р
а
е
к
и
с
о
ж
е
а
с
з
а
м
у
р
ц
е
и
с
т
и
ч
а
ма
и
в
н
и
?
в
р
я
ж
и
е
:
м
а
г
д
и
н
эл
э
л
е
им
яж
ч
е
м
п
и
и
е
о
т
н
а
я
ц
с
и
н
х
е
м
в
л
е
а
ф
а
к
л
ю
с
к
е
н
и
с
л
е
а
в
и
р
а
в
е
п
и
т
о
р
а
ю
а
к
р
н
о
с
в
ы
ч
ж
е
н
з
н
г
н
и
н
а
м
ек
т
е
к
т
м
п
ж
е
н
м
у
и
с
г
а
н
о
с
ц
е
п
н
у
с
м
о
е
н
и
а
м
ю
ч
е
о
н
и
я
е
д
у
и
с
я
в
н
и
п
р
п
тс
я
р
и
в
с
т
и
ч
и
с
н
и
я
н
а
ч
и
т
н
ми
т
р
и
т
р
и
п
р
и
н
и
я
е
м
а
р
м
с
и
т
п
ь
с
о
и
й
и
я
м
о
ж
е
К
н
д
е
к
л
у
ю
щ
я
т
о
с
п
о
с
п
о
д
я
л
вы
и
?
с
л
я
я
?
ч
е
н
н
о
и
ч
е
и
ч
и
ч
е
и
б
о
я
?
п
р
м
к
о
м
о
н
т
е
л
,
с
и
д
а
si
g
1
0
жн
К
1
е
н
с
лю
щи
и
с
о
п
с
т
о
д
к
л
л
и
ы
х
т
яю
н
и
я
й
(
е
с
к
ес
к
е
с
к
о
р
о
р
и
о
с
т
н
и
к
л
ь
н
с
хе
а
л
ь
g
.
Н
0
0
н
о
н
а
с
ат
ю
ч
а
П
и
е
н
д
п
р
о
о
я
н
лю
п
т
о
к
ю
тс
я
я
т
(
к
о
й
к
о
й
к
о
й
о
м
т
ь
ю
к
и
н
о
м
а
ь
н
о
На
О
м
н
а
а
э
к
ор
а
К
П
о
д
во
д
у
к
о
т
и
н
н
о
ю
ч
е
о
к
а
я
т
о
к
)?
й
(
й
(
й
с
м
у
в
ю
ф
с
о
ос
и
а
к
о
г
о
а
з
а
м
.
а
б
л
к
р
а
о
м
2
.
д
г
о
п
р
к
т
и
и
в
л
о
г
о
е
н
ф
о
п
р
д
е
к
а
)
(
с
в
ы
м
о
ж
в
е
л
фо
о
д
е
и
а
6
от
о
о
аж
П
о
л
ю
д
а
н
е
м
и
о
т
о
р
о
с
и
в
н
л
е
н
о
т
о
к
о
р
м
р
и
е
й
с
и
н
)
?
)?
ып
ж
н
о
л
и
ч
о
р
м
е
р
ж
а
б
с
6
5
о
р
пе
ж
и
м
о
э
т
д
а
т
е
о
и
л
и
о
в
к
с
ы.
н
о
е
ни
о
к
и
м
е
в
к
с
тв
н
а
п
п
р
я
о
з
ч
е
н
м
а
жи
с
ц
и
о
й
р
и
мы
т
о
м
т
ь
о
с
ц
и
к
к
а
е
и
и
е
к
а?
и
ст
к
р
к
л
ю
у
ю
п
р
я
м
и
з
а
ф
н
и
и
к
р
и
т
р
и
с
с
й
п
о
и
о
д
ы
о
му
к
р
ц
и
л
к
ат
у
к
и
е
к
а
т
оч
р
и
в
юч
ющ
я
ж
и
т
е
фи
и
р
и
в
р
а
з
с
?
о
к
д
и
ч
сц
у
п
р
и
в
л
л
о
уш
р
а
ем
т
у
ш
н
и
вы
е
н
щ
и
е
ж
е
н
е
л
е
кс
а
в
о
й
з
л
о
аз
а
ч
е
с
и
л
р
и
в
у
ю
о
г
р
ш
к
о
а
б
о
м
к
о
шк
и
к
у
ы
е
н
и
и
е
з
н
и
я
е
м
и
р
а
к
т
й
т
о
ж
а
н
а
с
к
о
л
л
о
и
з
а
ю
э
р
а
ф
о
й
о
т
е
о
с
т
к
и
у
н
то
и
п
з
н
а
я
и
(
р
о
в
т
и
в
т
о
к
ен
а
н
о
г
о
о
г
р
ам
э
т
о
ф
а
и
н
е
т
н
о
и
н
н
е
с
ка
п
ос
а
ч
е
и
з
м
)
?
в
ат
в
н
о
к
а
с
ие
н
а
р
о
н
р
а
ф
м
к
н
о
г
о
м
о
н
д
у
о
е
н
д
у
с
и
н
и
ле
е
н
и
м
е
р
?
ь
м
о
г
о
с
т
а
в
ри
н
а
п
ф
а
н
у
т
о
н
ож
у
к
т
с
о
у
к
т
н
у
с
н
д
о
и
я
р
я
ю
мг
о
а
н
о
р
я
и
с.
п
р
я
п
о
т
о
м
н
а
п
ж
н
о
т
и
в
о
п
р
т
и
в
с
о
и
ап
о
в
а
н
е
ю
т
г
н
о
с
о
в
и
я
д
Ф
1
1
я
ж
о
д
а
м
к
п
р
я
о
у
в
н
о
р
о
т
в
н
о
и
д
а
ря
те
л
е
с
и
п
р
о
в
е
с
о
п
и
т
с
Фу
1
.1
,
ж
е
н
а
е
т
к
л
ю
я
ж
е
у
в
и
о
с
т
т
и
в
о
с
т
а
л
ь
ж
е
л
ь
н
и
н
р
и
е
н
н
п
р
о
с
я
у
р
ь
,
п
н
и
я
т
с
я
юч
е
н
и
и
д
е
т
и
в
л
е
т
и
ь
н
о
е
н
и
н
о
у
с
бо
н
о
е
о
т
и
м
е
ь
е
к
п
и
т
я
,
п
я
н
ч
е
К
и
я
е
т
ь
в
е
н
и
с
о
г
о
и
я
?
с
о
и
р
ы
е
з
и
в
л
е
н
е
кр
т
ае
т
пр
н
а
п
К
1
.
П
ь
к
р
за
и
е
п
а
о
?
К
р
е
и
д
а
ы
с
з
н
а
л
е
н
е
е
и
в
тс
я
р
е
д
п
р
я
н
а
П
р
и
р
и
в
и
о
т
а
р
а
н
а
К
а
к
е
з
и
а
л
ь
с
л
е
а
ч
е
н
и
я
и
с
в
о
й
я
д
-
я
-
а
и
и
-
и
-
т
а
-
а
-
к
и
-
ь
-
е
-
е
-
я
с
-
й
,
66
Программа работы
1. Открыть файл LW 11, извлечь из поля компонентов
Favorites подсхему sig с номером своего варианта, а из поля КИП
(
Instruments) – осциллограф (Oscilloscop). Собрать остальную часть
схемы, показанной на рис. 11.1.
2.
Проградуировать осциллограф в единицах напряжения, тока
и времени. Для этого на шкале управления осциллографом выставить
масштаб: по напряжению – 100 В/дел., по времени – 200 mс/дел. Мас-
штаб тока при этом будет равен 500 мА/дел.
3.
При замкнутом ключе К
1
снять осциллограмму несинусои-
дального напряжения источника. При помощи кнопки
Pause, которая
находится под кнопкой
Пуск в правом верхнем углу экрана, получить
изображение полного периода несинусоидального напряжения. Затем с
помощью кнопки
Expand на панели управления осциллографом полу-
чить увеличенное изображение экрана осциллографа. Обратный пере-
ход осуществляется кнопкой
Reduce. Перечертить осциллограмму на
миллиметровку. Записать показание вольтметра.
4.
Снять осциллограмму тока в цепи с индуктивностью, для
чего необходимо разомкнуть ключ К
1
, и ключ К
2
переключить на ин-
дуктивность. Записать показание амперметра.
5.
Снять осциллограмму тока в цепи с емкостью, для чего пе-
реключить К
2
в положение емкости. Записать показание амперметра.
6.
Разложить кривую напряжения в п. 3 и кривые тока в п. 4 и
п. 5 в ряд Фурье на гармоники не выше пятой и определить действую-
щие значения напряжения и тока, сравнив их с показаниями вольтметра
и амперметра.
Действующие значения тока и напряжения определяются по фор-
мулам:
22 2
135
2
mmm
UUU
U
++
=
;
22 2
135
2
mmm
I
II
I
++
=
.
7.
Записать мгновенные значения одной из величин напряже-
ния или тока по указанию преподавателя, построить её гармонические
составляющие и, сложив их графически, сравнить результат с исходной
кривой, полученной экспериментально.
8.
Сделать выводы по работе.
67
РАБОТА 12
ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ
В ЦЕПЯХ ПЕРВОГО ПОРЯДКА
Цель работы.
Исследование переходных процессов в цепях с кон-
денсатором, характеризующихся дифференциальными уравнениями
первого порядка.
Пояснения к работе
При всяком изменении режима работы цепи, содержащей хотя бы
один накопитель электрической энергии (индуктивность
L или емкость
C) возникают переходные процессы – процессы перехода от одного ус-
тановившегося режима к другому. Мощность реальных источников в
цепи конечна, поэтому связанные с энергией величины – ток в индук-
тивности и напряжение на емкости – могут изменяться только плавно,
без скачков. В этом суть законов коммутации.
Решение системы дифференциальных уравнений, характеризую-
щих состояние цепи,
может быть найдено в виде суммы принужденной
и свободной составляющих. Например, для тока:
i = i
пр
+ i
св
.
Принужденная составляющая при постоянных и периодических
источниках определяется из расчета установившегося режима (
t → ∞)
послекоммутационной цепи и вид ее соответствует характеру источни-
ков.
Свободная составляющая записывается в виде суммы экспонент
св
k
pt
k
iAe=
∑
при различных вещественных корнях характеристиче-
ского уравнения
p
k
.
Постоянные интегрирования А
k
определяются из начальных ус-
ловий – зависимых и независимых.
Независимые условия (начальные значения тока в индуктивности и
напряжения на емкости) определяются по законам коммутации и тре-
буют предварительного расчета установившегося режима докоммута-
ционной цепи. Начальные же значения остальных величин (зависимые
условия) определяются из уравнений, описывающих состояние после-
коммутационной цепи в первый
момент после коммутации (t = +0).
В цепи с одним накопителем свободная составляющая содержит
только один корень и одну экспоненту. Например, для схемы рис. 12.1,
а
i
св
=
p
t
k
k
A
e
, причем i = i
св
, поскольку в установившемся режиме посто-
янный ток через конденсатор не течет и
i
пр
= 0. До коммутации конден-
сатор не был заряжен, так что по второму закону коммутации
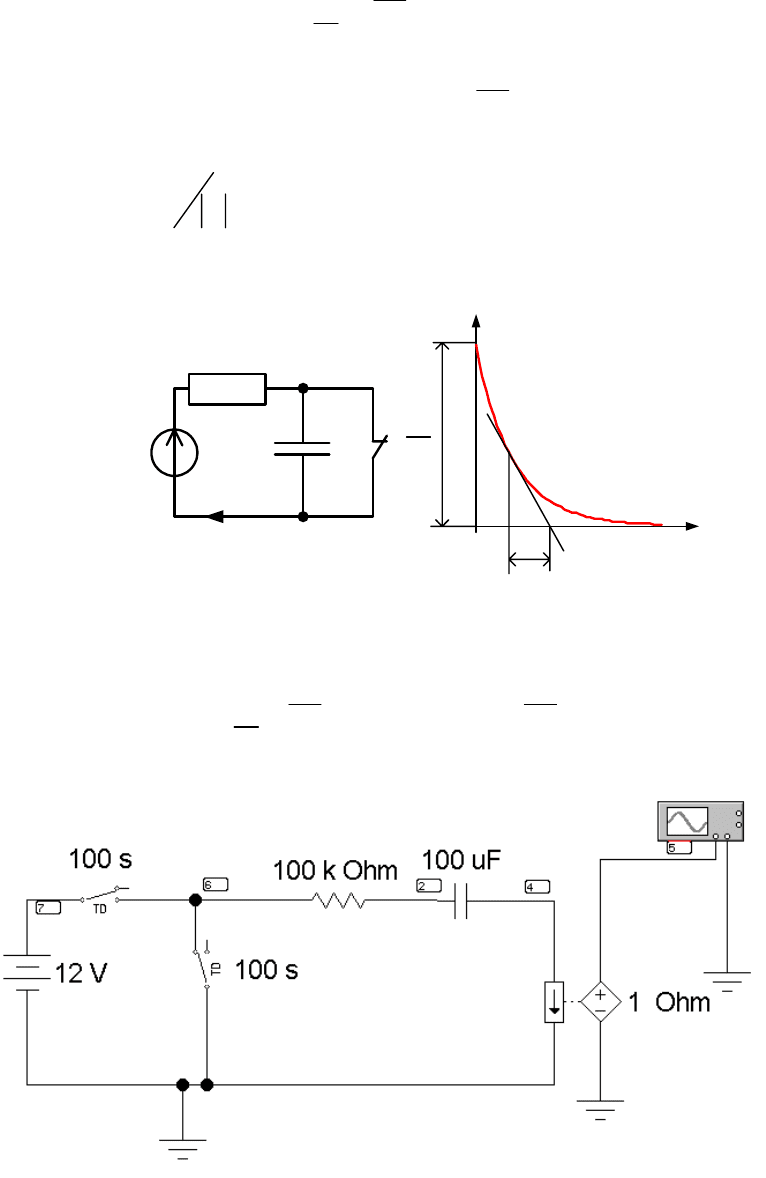
68
u
С
(+0) = u
C
(–0) = 0. Поэтому А = i
св
(0) = [U – u
C
(+0)]/R.. Тогда ток и
напряжение при заряде конденсатора
() ,
() () (1 )
t
RC
t
RC
C
U
it e
R
ut UitRU e
−
−
⎫
⎪
=
⎪
⎬
⎪
⎪
=− = −
⎭
(12.1)
Здесь корень характеристического уравнения
p = –(RC)
–1
, а посто-
янная времени
1
τ RC
p
==
. Она может быть найдена по эксперимен-
тально полученной зависимости
i(t) как длина подкасательной
(рис. 12.1,
б).
R
U
C
()it
()it
τ
U
R
t
,
I
мкА
Рис. 12.1
Аналогичным образом могут быть получены выражения для тока и
напряжения при разряде конденсатора на сопротивление
R:
() ; () .
tt
RC RC
С
U
it e u t Ue
R
−−
=− = (12.2)
Схема электрической цепи
Рис. 12.2

п
П
в
в
т
ц
В
U
R
C
В
U
R
C
В
U
R
C
(
t
в
в
п
м
д
п
о
л
Пи
в
е
л
в
и
и
ты
ц
е
с
В
а
р
U
R
C
В
а
р
U
R
C
В
а
р
U
R
C
(
D
t
a
t
в
е
р
в
о
д
п
о
мы
д
р
у
л
ь
з
и
т
а
л
и
ч
и
с
ы
в
а
с
с
а
ри
ри
ри
П
el
e
t
e)
р
т
и
д
о
в
сл
ыш
у
г
о
Д
л
з
у
е
а
н
и
чи
с
в
а
н
и
а
(
и
а
н
В
к
О
м
к
и
а
н
В
к
О
м
к
и
а
н
В
к
О
м
к
Пр
e
t
e
и
и
к
а
П
о
в
п
е
п
ш
и
о
г
о
л
я
е
т
с
и
е
и
н
а
в
а
р
и
я
5τ
н
т
Ом
кФ
н
т
Ом
кФ
н
т
Ом
к
Ф
р
о
ц
e
),
в
м
а
л
и
о
с
л
п
р
о
п
о
я
и
о
к
и
с
с
я
ц
е
а
к
о
и
а
к
л
=
м
Ф
м
Ф
м
Ф
ц
е
с
вы
м
е
н
и
и
л
е
о
в
о
я
в
л
п
о
к
о
м
с
с
л
э
л
е
п
и
о
т
о
а
н
т
л
ю
ч
5 ⋅
1
1
0
1
0
1
0
1
1
1
0
2
0
1
0
2
1
1
0
1
1
1
0
с
с
ы
р
е
н
я
т
и
л
и
ра
о
д
н
л
е
н
о
я
в
м
п
о
л
е
д
л
е
к
и
о
о
р
о
т
о
м
ч
е
й
R
C
0
0
0
0
0
1
0
0
0
0
0
1
0
1
0
0
0
с
о
е
з
а
т
ь
и
п
а
з
м
н
и
н
и
я
в
л
я
о
н
д
о
в
к
т
р
о
с
у
о
г
о
м
,
у
й
д
C
)
Ис
о
зд
а
ть
ег
о
п
о
г
м
е
щ
ка
м
я
ж
я
ю
ен
в
а
н
р
и
ч
ущ
о
U
у
к
а
д
о
л
.
2
11
1
2
1
0
1
2
11
2
2
1
0
2
2
11
13
1
0
с
с
л
а
н
р
р
(
G
о
п
г
о
р
щ
е
н
м
и
жи
щ
и
та
н
и
я
ч
е
с
щ
ес
т
U
,
а
з
а
лж
2
2
0
0
2
2
0
0
0
0
0
л
е
д
н
и
я
ро
м
ы
р
а
п
о
не
н
а
п
р
ко
G
u
п
а
р
р
и
з
ни
и
.
К
и
р
н
и
й
с
д
о
я
п
с
к
а
т
в
л
а
т
а
н
н
ж
н
о
3
1
1
1
1
1
2
1
2
1
1
1
д
о
в
я
с
х
о
в
ыш
сп
о
д
г
н
т
а
м
и
р
ав
то
р
t),
р
а
м
з
о
н
и
я
К
у
р
н
о
й
с
я
о
п
п
р
а
я
л
я
е
т
а
к
н
ы
о
б
3
1
2
1
3
3
1
0
0
1
3
1
2
2
3
3
1
0
0
2
3
1
2
1
4
3
1
0
0
в
а
н
х
е
м
и
з
ш
ь
ю
о
л
г
о
т
т
о
в
и
ч
е
о
й
ро
в
с
м
е
н
т
а
ко
р
с
о
й
ч
п
р
п
о
я
о
ц
ц
е
е
т
с
кж
м
п
б
ы
т
3
0
3
0
3
0
н
и
е
El
мы
з
ю
н
л
о
ж
т
ов
в
н
а
е
с
к
й
к
о
го
с
т
а
тр
а
л
и
м
п
о
р
ч
е
р
р
и
я
в
л
ц
ес
е
п
ь
с
я
ж
е
з
п
р
т
ь
4
1
1
1
1
1
2
1
2
1
1
1
е
п
l
e
c
ы
н
б
и
н
е
о
ж
е
н
ле
а
р
к
и
м
к
н
о
а
в
л
ы
и
(
п
о
н
м
ы
р
н
о
э
т
л
е
н
со
в
ь
,
с
о
т
з
н
а
е
п
б
о
4
3
4
7
0
0
4
3
2
4
7
0
0
2
4
3
6
0
0
0
п
е
р
c
tr
o
н
а
ч
и
б
л
о
б
х
н
и
е
н
н
р
а
б
м
о
п
к
м
о
л
я
т
(
C
(
Fl
н
е
н
ыш
о
й
т
о
м
н
и
я
6
в
с
х
е
т
и
а
ч
е
п
о
д
о
л
ь
7
0
7
0
0
0
р
е
х
o
n
ч
и
н
л
и
о
х
о
д
е
к
н
ы
м
б
о
ч
м
е
к
и
ож
т
ь
(
C
o
m
ip
н
т
о
ш
и
то
м
я
н
6
9
за
р
ем
и
с
т
е
н
и
д
ав
ьш
5
1
4
2
0
1
0
1
5
1
4
3
0
1
0
2
5
1
4
1
9
1
0
х
о
д
ic
s
н
а
е
о
т
е
ди
к
о
м
м
э
ч
е
м
е
н
ю
м
ы
ж
н
о
(
P
a
mp
V
e
о
в
п
о
ч
к
п
р
н
а
н
р
я
д
м
а
т
о
ч
и
я
ат
е
ш
е
д
4
0
0
0
0
5
4
0
0
0
0
5
4
9
0
0
0
д
н
ы
s
W
е
т
с
е
к
и
м
ы
мп
э
с
к
м
п
ю
,
ыш
о
a
s
t
p
o
n
e
r
t
п
р
о
д
в
к
и
(
р
о
в
н
е
м
д
а
ко
ч
н
и
R
е
л
е
д
л
и
ых
W
o
r
с
я
п
ы
х
п
о
н
к
и
з
п
о
л
в
ш
и
к
о
t
e)
n
e
n
t
ic
a
р
о
и
в
о
д
(
у
з
в
о
д
м
т
и
то
р
и
к
а
и
ем
и
т
6
3
2
2
4
7
1
6
3
3
2
4
7
2
6
3
4
2
4
7
х
п
р
r
k
b
с
в
п
р
о
э
л
н
е
н
з
о
м
л
е
в
с
п
п
о
п
и
и
n
t
a
l,
и
з
в
д
и
т
з
л
а
д
н
и
т
а
к
р
р
о
а
п
C
м
и
з
ел
ь
2
7
0
6
2
7
0
6
2
7
0
р
о
b
e
n
вы
о
г
р
л
е
м
н
т
о
м
.
м
о
п
л
ы
п
о
и
р
о
п
о
P
r
F
l
в
о
д
тс
я
а
)
н
и
к
к
о
й
р
аз
р
й
п
о
с
в
ы
з
т
ь
н
7
4
2
4
1
4
3
4
2
4
5
4
ц
е
n
c
h
ы
б
о
р
а
м
м
е
н
о
в
П
р
о
ж
н
ы
в
а
к
о
о
в
а
о
в
о
r
o
p
l
ip
д
и
т
я
к
н
а
ж
п
р
й
ж
р
я
д
п
о
с
т
о
ы
б
и
т
а
б
ос
т
7
4
2
2
4
7
0
1
7
4
3
2
4
7
0
2
7
4
5
2
4
7
0
е
сс
о
h
о
р
а
м
м
ы
н
т
о
с
х
р
и
н
о
а
ю
о
м
п
а
т
ь
о
р
а
p
e
r
H
т
с
я
к
в
ы
жи
р
о
т
ж
е
д
а
о
к
а
о
я
н
и
р
а
б
л.
т
и
0
0
0
о
в
а
э
л
ы
о
в
х
е
м
р
а
в
о
ю
щ
и
п
о
н
ь
а
ч
и
r
ti
H
o
r
я
с
ыв
и
м
а
т
я
г
ж
и
к
о
а
за
н
н
о
аю
1
2
п
8
4
3
4
1
4
4
4
2
4
5
4
в
с
л
е
м
(
п
н
а
м
ы
а
з
м
о
с
п
им
н
е
н
(
C
и
в
а
es
)
r
iz
o
с
о
е
в
о
д
а
е
т
г
и
в
и
р
н
он
н
а
о
г
о
ю
т
с
2
.1
ер
8
4
3
3
4
7
0
1
8
4
4
3
4
7
0
2
8
4
5
3
4
7
0
с
р
е
м
е
п
е
р
а
р
в
м
е
щ
п
о
л
м
п
н
т
у
Co
а
т
ь
)
,
о
o
n
t
е
д
и
д
у
т
с
я
в
а
е
н
о
й
н
де
а
н
о
н
с
я
в
.
В
е
х
о
Т
0
0
0
е
д
е
н
т
р
е
т
р
а
б
с
о
ще
л
ь
з
п
о
с
у
,
o
p
y
ь
э
л
о
т
о
t
a
l
и
н
е
к
о
я
л
е
т
с
й
т
е
н
с
н
а
н
а
п
в
с
В
р
е
о
д
аб
9
5
3
3
4
7
1
9
5
4
3
4
7
2
9
5
6
3
4
7
е
т
ов
т
а
с
б
о
ч
о
о
е
н
и
з
о
в
с
л
е
c
y
),
л
е
м
о
б
р
l
).
е
н
и
о
м
п
л
ев
с
я
т
о
ч
с
ат
р
и
п
р
я
с
о
о
е
м
я
н
о
л
и
3
7
0
9
3
7
0
9
3
7
0
и
с
к
и
ч
и
й
тв
е
и
и
в
а
т
е
п
о
у
ме
р
а
з
и
е
п
о
н
ая
к
ч
к
и
ор
и
с.
яж
о
т
в
я
с
о
го
и
ц
а
п
р
и
в
а
й
с
е
т
с
к
о
т
ь
с
щ
е
о
м
о
у
д
е
н
т
з
и
т
и
х
н
е
н
к
н
в
ы
и
,
п
а
1
2
ж
е
н
в
е
т
с
р
а
п
р
а
1
1
0
6
4
7
4
7
2
0
6
5
7
4
7
3
0
6
6
7
4
7
р
и
а
н
и
с
т
о
с
т
в
о
м
п
с
я
д
е
л
ч
ощ
ал
я
т
(
R
т
ь
х
в
н
т
а
н
о
п
ы
в
о
п
о
с
и
с
2
.
2
н
и
я
т
с
т
а
б
а
р
о
1
2.
1
0
7
7
0
0
7
7
0
0
7
7
0
б
о
и
е
м
о
л
)
в
и
и
п
о
д
и
ч
к
а
щ
ь
ю
я
т
ь
R
o
п
о
в
ы
а
,
и
п
к
а
о
д
у
с
л
е
с
-
2
.
я
,
т
-
а
-
о
-
1
о
-
м
)
,
и
о
-
и
-
а
ю
ь
o
-
о
ы
-
и
а
у
е
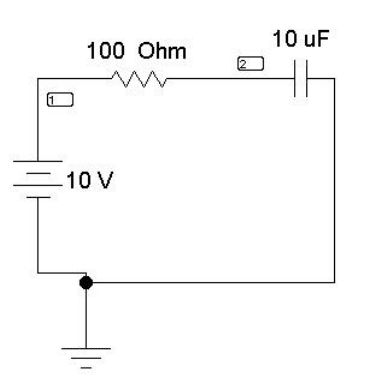
70
чего левая кнопка мыши опускается и соединение готово. Подключение
измерительных приборов выполняется аналогично подключению ком-
понентов схемы. При этом можно использовать цветные проводники,
которые выделяют подключенный прибор и окрашивают в соответст-
вующий цвет выводимые графики. Для изменения цвета проводника
нужно два раза щелкнуть левой кнопкой мыши на изображение и в
от-
крывшемся окне выбрать нудный цвет. Для начала анализа схемы сис-
темой необходимо активизировать схему нажатием кнопки
6, для оста-
новки анализа – кнопку
7. Чтобы сохранить рабочий лист (документ)
под нужным названием, необходимо щелкнуть мышью по третьей
кнопке в третьей строке сверху – пиктограмме с изображением дискеты.
Появится диалоговое окно
Save as (Сохранение). В текстовом поле File
name
(Имя файла) нужно дать имя файлу (документу). Система автома-
тически добавит расширение
.ewb.
Итак, перед нами готовая схема (рис. 12.3).
Если переходный процесс возникает в результате включения схе-
мы, как в данном случае, то никаких коммутаторов не требуется.
Сначала необходимо установить нумерацию контрольных точек в
схеме. Для этого необходимо раскрыть диалоговое окно
Show Hide (по
пути
Circuit > Schematic Options > Show/Hide). Окно показано на
рис. 12,4. В окошке Show nodes курсором мыши необходимо сделать
отметку. Щелкнуть кнопку
ОК, после чего появится нумерация точек
соединения элементов
Рис.12.3
Наиболее быстрый способ пронумеровать узлы – кликнуть правой
клавишей мыши на свободном участке рабочего поля, в выпавшем ме-
ню выбрать пункт
Schematic Options, что приведёт к открытию окна
