Куцый Н.Н. Теория оптимального управления. Лабораторный практикум
Подождите немного. Документ загружается.


МИНИСТЕРСТВО ОБРАЗОВАНИЯ PОССИЙСКОЙ ФЕДЕPАЦИИ
ИPКУТСКИЙ ГОСУДАPСТВЕHHЫЙ
ТЕХHИЧЕСКИЙ УHИВЕPСИТЕТ
ТЕОРИЯ
ТЕОРИЯ
ОПТИМАЛЬНОГО
ОПТИМАЛЬНОГО
УПРАВЛЕНИЯ
УПРАВЛЕНИЯ
ЛАБОРАТОРНЫЙ ПРАКТИКУМ
Лабораторные работы № 1, 2.
Иркутск - 2001 г.
Куцый Н.Н. Теория оптимального управления. Лабораторный практикум:
Лабораторные работы № 1,2. – Иркутск, изд-во Иркутск. гос. технич. ун-та,
2001. – 25с.
Приведены варианты заданий лабораторных работ по учебной дисциплине
"Теория оптимального управления". Дан необходимый теоретический и спра-
вочный аппарат. Предназначен для студентов специальностей 220100 – "Вычис-
лительные машины, системы, сети и комплексы", 220200 – "Автоматизирован-
ные системы обработки информации и управления", 071900 – "Информацион-
ные системы в технике и технологиях".
Библиогр. 6 назв.
Рецензент: к.т.н. Федорещенко Н.В.
Подготовила к печати: Брянская А.Г.
Подписано в печать Формат 60х84 1/16.
Бумага типографская. Печать офсетная. Усл. печ. л.
Уч.-изд. л. Тираж 100 экз. Зак.
ЛР № 020263 от 30.12.96
Иркутский государственный технический университет
664074, Иркутск, ул. Лермонтова, 83
2

ЛАБОРАТОРНАЯ РАБОТА № 1
РАСЧЕТ НА ЭВМ ОПТИМАЛЬНЫХ ПАРАМЕТРОВ ПИД-РЕГУЛЯТОРА
Цель работы - ознакомление с методикой расчета оптимальных парамет-
ров регулятора при заданной структурной автоматической системы регулирова-
ния и заданных параметрах объекта регулирования по интегральным критериям
качества процесса регулирования с использованием средств вычислительной
техники.
1.ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Одной из задач оптимального управления является синтез автоматических
систем по тому или иному интегральному критерию качества (оценке опти-
мальности), различая при этом задачи структурного и параметрического синте-
за.
Под задачей структурного синтеза при заданном объекте регулирования
будем понимать выбор закона формирования регулирующего воздействия, поз-
воляющего обеспечить заданные характеристики процессов протекающих в ав-
томатических системах.
Задача параметрического синтеза предполагает заданной структуру авто-
матической системы и необходимость нахождения настраиваемых параметров
регулятора, обеспечивающих экстремум (обычно минимум) принятого крите-
рия качества процессов регулирования.
Понятно, что с точки зрения процесса решения задача структурного синте-
за более сложна в сравнении с задачей параметрического синтеза.
В данной лабораторной работе рассматривается решение задачи парамет-
рического синтеза (параметрической оптимизации).
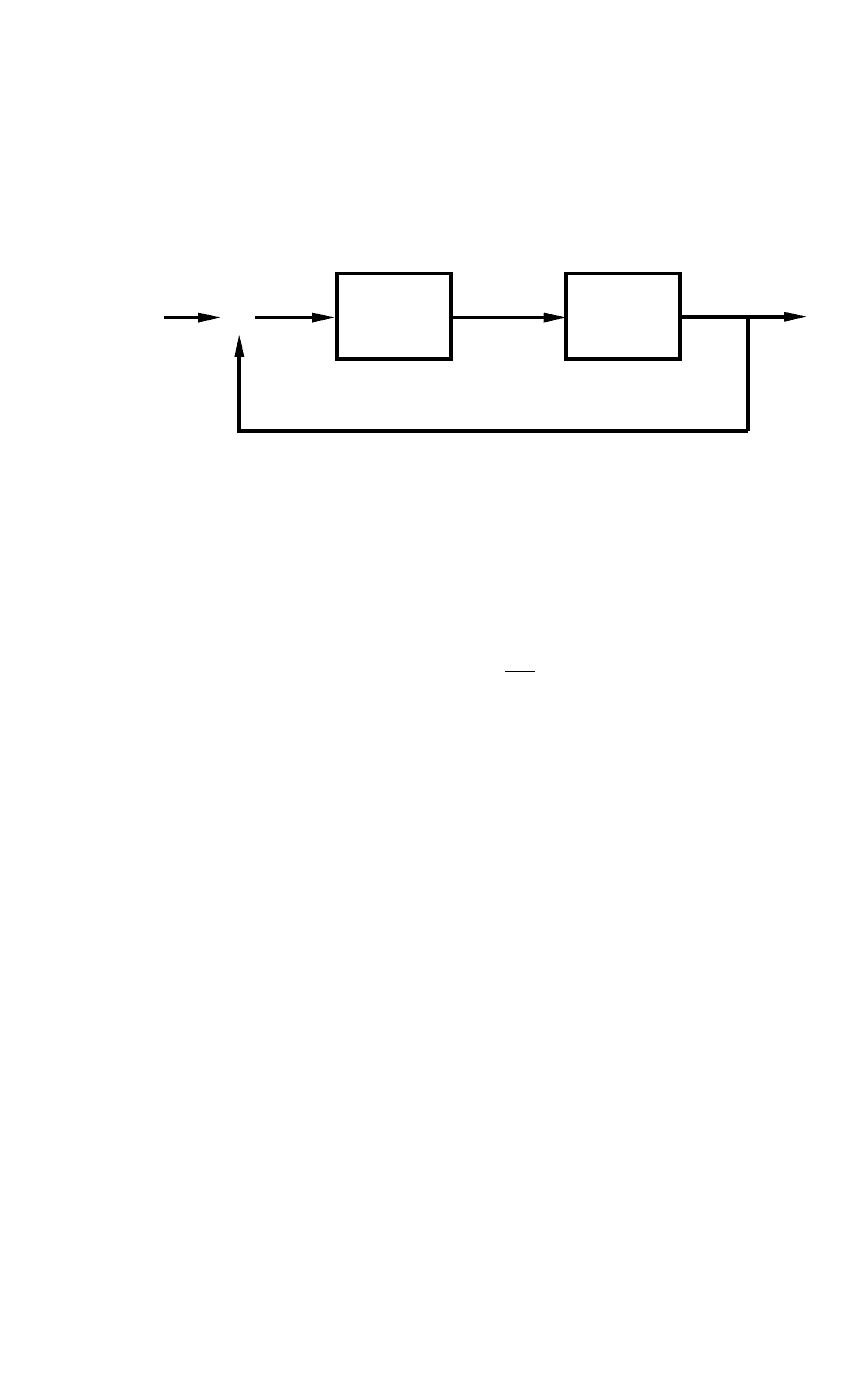
На рис. 1 представлена структурная схема автоматической системы, проте-
кающие процессы в которой можно описать
).()()(
),()()( )1(
),()()(
txpWtu
tupWty
tytgtx
рег
об
=
=
−=
Здесь
−
)(tx
ошибка регулирования;
−
)(tg
задающее воздействие;
−
)(ty
выход-
ная величина;
−
)(tu
регулирующее воздействие;
−
)( pW
об
передаточная функ-
ция объекта регулирования;
−
)( pW
рег
передаточная функция регулирующего
устройства.
Качество переходных процессов оценивается интегральным критерием, об-
щий вид которого может быть записан
∫
∞
−
−
+++=
0
2)1(2
1
22
1
2
,))(( )2( dtxxxI
n
n
µµ
3
где
−
−
)1(
,,,
n
xxx
отклонение регулируемой величины и ее производные по
времени;
−
−
11
,,
n
µµ
весовые коэффициенты.
Первый член в подынтегральной функции (2) запрещает длительное суще-
ствование отклонения
x
, а последующие члены - длительное существование
больших значений производных. Тем самым минимуму интеграла
I
соответст-
вует достаточно быстрый и плавный переходный процесс.
g
(
t)
(-)
x
(
t)
u(t)
y(t)
Рис. 1.
⊗
)( pW
рег
)( pW
об
Структура регулятора задана и представляет собой пропорционально-инте-
грально-дифференциальный закон регулирования (ПИД-закон регулирования),
передаточная функция которого имеет вид
,)()( pq
p
q
qpW
рег
3
2
1
3
++=
где
−
321
qqq ,,
настраиваемые параметры, значения которых необходимо опре-
делить, исходя из минимума заданного критерия качества.
Регулятор с таким алгоритмом работы осуществляет перемещения регули-
рующего органа в каждый момент времени пропорционально отклонению регу-
лируемой величины, интегралу и производной ошибки регулирования.
В случае только пропорционального регулирования, т.е. при формирова-
нии регулирующего воздействия по алгоритму
),()(
1
txqtu
=
автоматическая система в общем случае является статической, так как при лю-
бом конечном значении настраиваемого параметра
1
q
установившаяся ошибка
будет отличной от нуля.
Интегральный регулятор формирует регулирующее воздействие, величина
которого пропорциональна интегралу ошибки регулирования, т.е.
∫
=
t
dttxqtu
0
2
,)()(
и тем самым выходной сигнал И-регулятора изменяется до тех пор, пока ве-
личина ошибки
)(tx
не станет равной нулю.
ПИ-регулятор (называемый так же изодромным) совмещает свойства про-
порционального и интегрального способов регулирования; ошибка регулирова-
4

ния, присущая пропорциональному регулированию, полностью исчезает, в то
время как скорость регулирования уменьшается незначительно.
Регулирование по производной не имеет самостоятельного значения, так
как в установившемся состоянии производная от ошибки равна нулю и тем са-
мым регулирование прекращается. Однако оно может играть весьма большую
роль в переходных процессах, так как такая такое регулирование позволяет
учитывать не только наличие ошибки, но и тенденцию к ее росту или уменьше-
нию.
В некоторых случаях в закон регулирования могут вводиться производные
более высоких порядков - вторая, третья и т.д., что в общем случае обеспечива-
ет улучшение качества процессов регулирования, но техническая реализация
вычисления производных второго порядка и выше, наталкивается на значитель-
ные трудности.
Объект регулирования в зависимости от задания описывается одной из
передаточных функций
p
pTpT
k
pW
об
обоб
об
об
τ
−
++
=
)1)(1(
)( )4(
21
,
,
12
)( )5(
22
p
pTpT
k
pW
об
обоб
об
об
τ
ζ
−
++
=
,
1
)( )6(
p
pT
k
pW
об
об
об
об
τ
−
+
=
,
)1(
)1(
)( )7(
2
1
p
pT
pT
kpW
об
об
об
обоб
τ
−
+
+
=
при заданных параметрах объекта регулирования
.,,,,,
21
обобобобоб
TTTk
τζ
В качестве критерия оптимизации в зависимости от номера задания ис-
пользуется один из рассмотренных ниже критериев.
Наиболее широко распространен в практике автоматического регулирова-
ния критерий
∫
∞
=
0
2
1
.)( )8( dttxI
Этот критерий носит название квадратичный интегральный критерий, ди-
намическая ошибка. Его распространение объясняется тем, что в распоряжение
исследователя (разработчика) автоматической системы теория предоставляет
аналитические зависимости между величиной этого критерия и параметрами
автоматической системы.
Критерий оптимизации вида
5
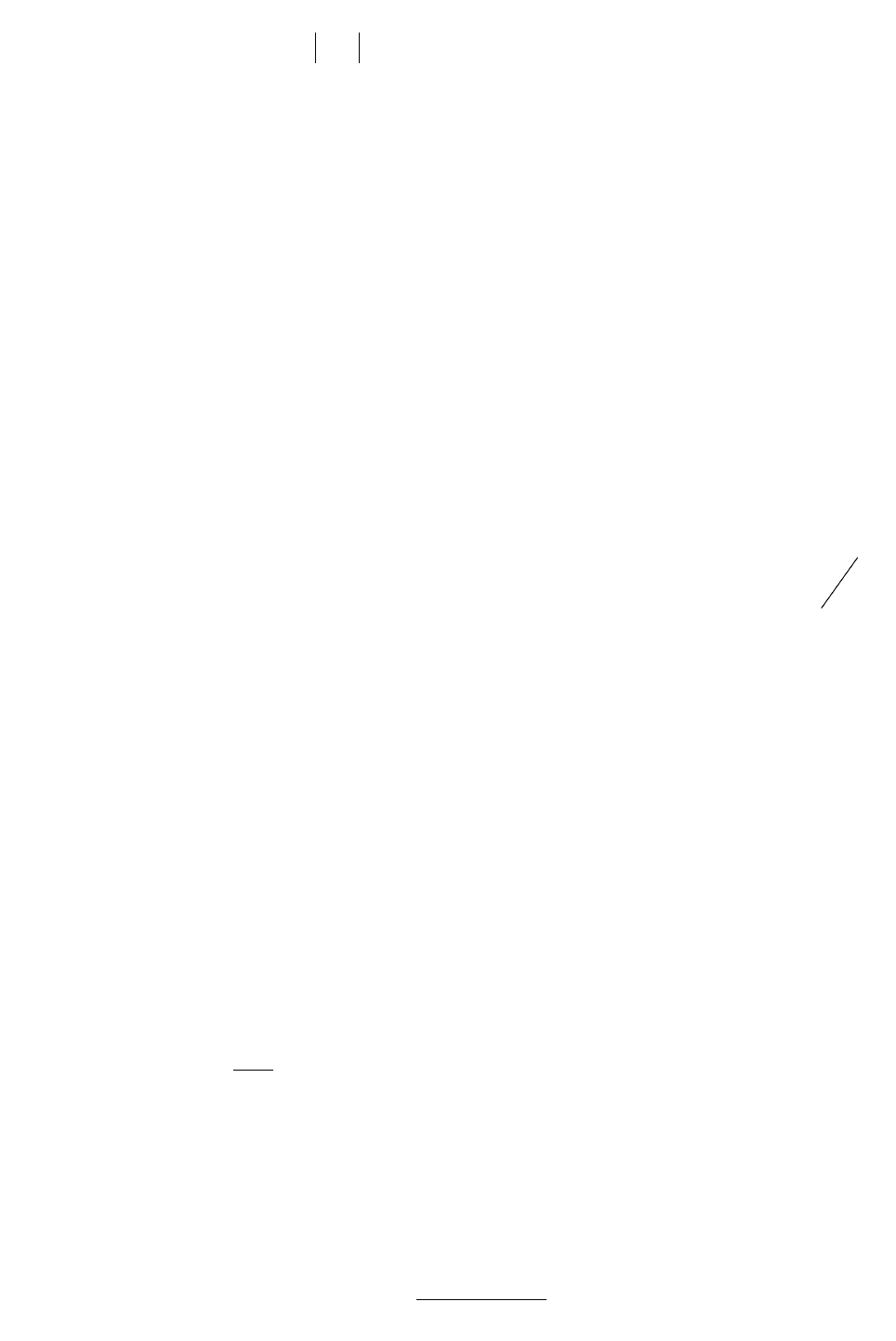
∫
∞
=
0
2
)( )9( dttxI
носит название модульного и получает распространение в последнее время в
связи с применением средств вычислительной техники для анализа и синтеза
автоматических систем в случае необходимости сужения числа используемых
аналитических зависимостей.
Конкретизируя выражение (2), запишем наиболее простую форму состав-
ного интегрального критерия
∫
∞
+=
0
222
3
.))()(( )10( dttxtxI
µ
Представим кратко каждый из методов градиентной итеративной процеду-
ры, применяемых в лабораторной работе в зависимости от номера варианта.
1.Метод релаксации. Алгоритм метода заключается в отыскании направ-
ления, вдоль которого критерий оптимизации уменьшается наиболее сильно.
Для этого в начальной точке работы алгоритма оптимизации определяются со-
ставляющие градиента по каждому из настраиваемых параметров, т.е.
,
j
q
I
∂
∂
).,,( 321
=
j
По направлению с наибыстрейшим убыванием критерия оптимиза-
ции, которому соответствуют наибольшие по модулю составляющие градиента
производятся шаги до тех пор, пока не будет получено минимальное значение
критерия именно по этому направлению. Тогда вновь определяются составляю-
щие градиента по всем настраиваемым параметрам и вновь находится направ-
ление наибыстрейшего убывания критерия оптимизации, по которому произво-
дятся дальнейшие шаги и т.д.
Критерием останова алгоритма оптимизации является достижение таких
значений настраиваемых параметров, т.е. точки в пространстве
,Q
при движе-
нии из которой по любому направлению дальнейшего убывания критерия опти-
мизации не происходит. На практике в качестве признака достижения
*
q
часто
применяется условие, которое для рассматриваемого случая может быть пред-
ставлено
. )(
доп
∆≤
∂
∂
∑
=
2
3
1
11
j
j
q
I
При
0
→∆
доп
выражение (11) превращается в точное условие равенства
нулю составляющие градиента в точке оптимума.
Алгоритм изменения значений настраиваемых параметров для выбранного
направления может быть записан в виде следующей формулы
,
])[[(
][][][ )(
j
jj
q
llI
signlhlqlq
∂
−∂
×−−=
1
112
q
6
где
−
][lq
j
значение настраиваемого параметра на
−
l
ом шаге работы алгоритма
оптимизации;
−
][lh
величина
−
l
го шага, которая может изменяться по тому
или иному алгоритму;
−
sign
функция знака.
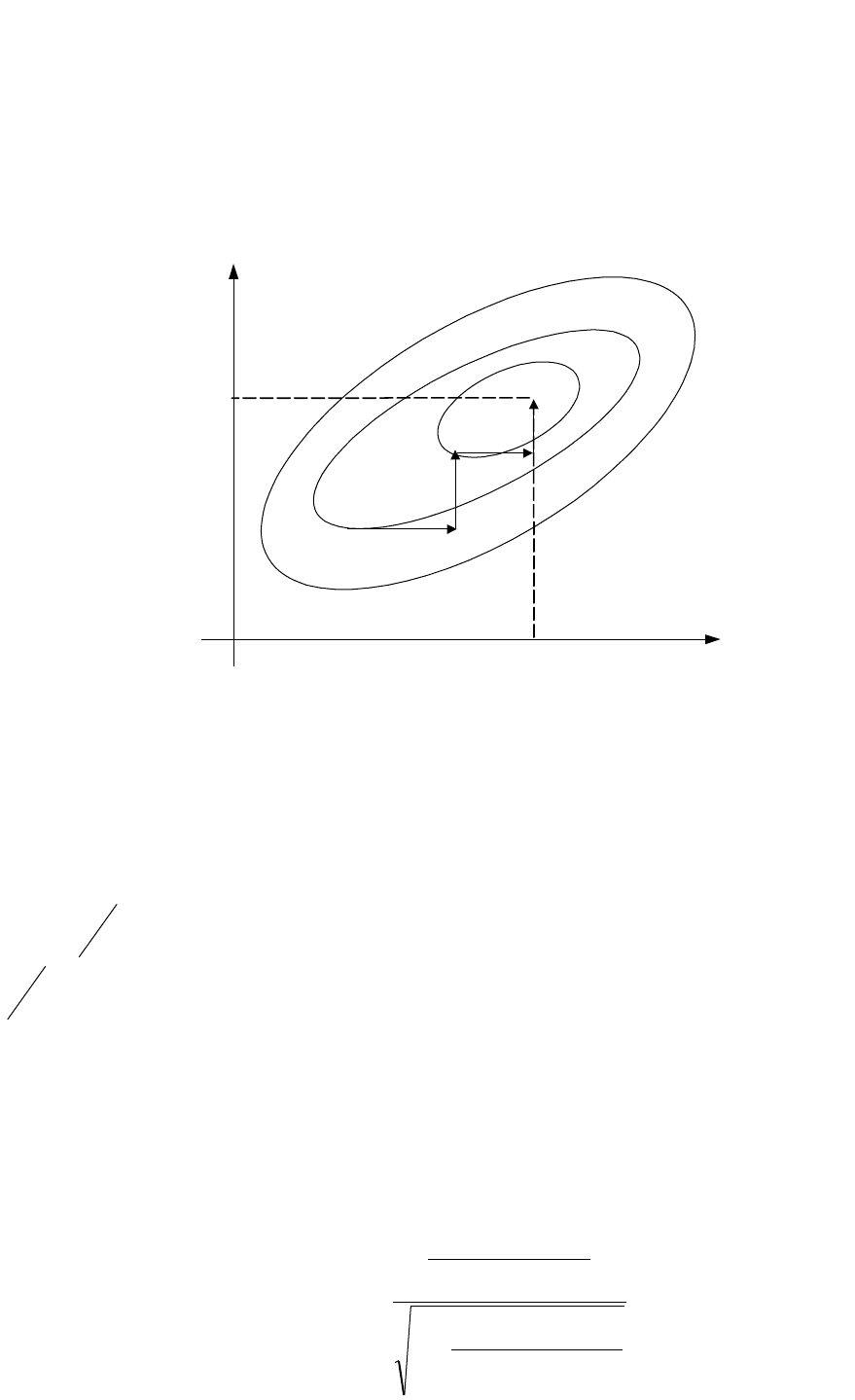
Графическое изображение движения алгоритма оптимизации от начально-
го значения вектора настраиваемых параметров
][0
q
к оптимуму
∗
q
в случае
двух настраиваемых параметров показано на рис. 2.
*
1
q
gradI
M
0
M
1
M
2
M
3
q
1
q
2
I=C
1
I=C
2
I=C
3
I
*
*
2
q
.
.
Рис. 2.
2.Метод градиента. При использовании этого метода шаги совершаются в
направлении наибыстрейшего уменьшения целевой функции, что, в общем слу-
чае, ускоряет процесс вычисления алгоритмом оптимизации значения
∗
q
.
Каждый шаг алгоритма оптимизации при использовании метода градиента
состоит из двух этапов. На первом вычисляются значения частных производ-
ных
))(( mj
q
I
j
11
=
∂
∂
по каждому из настраиваемых параметров. Величины
))(( mj
q
I
j
11
=
∂
∂
определяют направление градиента в рассматриваемой точке.
На втором этапе осуществляется шаг в направлении, обратном направлению
градиента, т.е. в направлении наибыстрейшего убывания целевой функции.
При выполнении шага одновременно изменяются значения всех настраива-
емых параметров. Каждый из них получает приращение, пропорциональное со-
ответствующей составляющей градиента.
Алгоритм градиентного метода может быть записан следующим образом
.
]))[,((
])[,((
][][][ )(
∑
=
∂
−∂
∂
−∂
−−=
m
j
j
j
jj
q
ltxI
q
ltxI
lhlqlq
1
1
1
113
q
q
7

В этом алгоритме для градиентного поиска применяется нормализованный
вектор градиента, который указывает лишь направление наискорейшего изме-
нения целевой функции, но не указывает скорости ее изменения по этому
направлению. При использовании нормализованного вектора-градиента шаг
спуска определяется величиной
],[lh
стратегию изменения которой можно
строить независимо от абсолютной величины градиента.
В случае использования алгоритма градиентного поиска в виде
),)(( ,
][(
][][][ )( mj
q
lI
hlqlq
j
jj
110114
=
∂
∂
−−=
q
величина шага
][lq
j
∆
при постоянном значении параметра
][0h
изменяется в
соответствии с изменением абсолютной величины градиента. Длина шага опре-
деляется выражением
).)(( ,
][(
][][ )( mj
q
lI
hlq
j
j
11015
=
∂
∂
−=∆
q
Алгоритм градиентного поиска (14) обладает тем достоинством, что при
приближении к оптимуму длина
][lq
j
∆
автоматически уменьшается.
3.Метод наискорейшего спуска. Идея метода наискорейшего спуска за-
ключается в следующем. После того как в начальной точке работы алгоритма
оптимизации вычислен градиент целевой функции и тем самым определено
направление ее наибыстрейшего убывания в этой точке, в данном направлении
делается шаг спуска. Если значение целевой функции в результате этого шага
уменьшилось, то производится очередной шаг в этом же направлении, и так до
тех пор, пока не будет найден минимум именно в этом направлении, после чего
вычисляется новое направление наибыстрейшего убывания целевой функции.
На рис. 3 показаны возможные траектории движения к оптимуму при при-
менении метода наискорейшего спуска (ломаная линия 1) и траектория движе-
ния к оптимуму при использовании метода градиента (ломаная линия 2).
Скорость движения к
*
q
зависит от того, насколько удачно выбрана ве-
личина шага
][lh
изменения независимых настраиваемых параметров
).3,2,1(
=
jq
j
При слишком малой величине
h
число шагов, которое необходи-
мо для достижения оптимума, будет большим, и, следовательно, потребуется
множество вычислений.
Если же величина шага с самого начала работы алгоритма параметриче-
ской оптимизации выбрана слишком большой, то вблизи оптимума, может воз-
никнуть "рыскание", так как при большой величине шага мала вероятность по-
падания в окрестность оптимума, в которой выполняется условие окончания
поиска (11).
8

*
1
q
gradI
q
1
q
2
I=C
1
I=C
2
I=C
3
I
*
*
2
q
.
.
1
2
Рис. 3.
При проведении параметрической оптимизации применяют алгоритмы из-
менения величины шага в процессе движения к
.
*
q
Суть одного из них доста-
точно простого и вместе с тем и эффективного состоит в следующем. пусть в
начале проведения параметрической оптимизации по направлению с наибы-
стрейшим убыванием критерия оптимизации задается некоторая величина шага
],0[h
равная например 0.1, что соответствует изменению значения настраивае-
мого параметра на 10% от принятого диапазона его изменения. С этим шагом
производится спуск по направлению с наибыстрейшим убыванием критерия оп-
тимизации до тех пор, пока для двух последующих вычисления значений крите-
рия оптимизации выполняется условие
]).[(])1[(( lIlI
qq
<+
16)
При нарушении этого условия на каком-либо
−
l
м шаге направление дви-
жения алгоритма параметрической оптимизации изменяется на обратное и дви-
жение продолжается с уменьшенной вдвое величиной шага, т.е.
.
при
при
)
−>
−≤
=+
])1[(])[(
2
][
])1[(])[(][
]1[17(
lIlI
lh
lIlIlh
lh
qq
qq
В результате использования такой стратегии величина шага спуска по
направлению с наибыстрейшим убыванием критерия оптимизации будет
уменьшаться в районе минимума критерия оптимизации по этому направлению
и поиск минимума можно прекратить, когда величина
][lh
обеспечивает изме-
нение величины критерия оптимизации меньше заданной точности определе-
ния минимума в этом направлении. Затем отыскивается новое направление с
наибыстрейшим убыванием критерия оптимизации и начальный шаг в этом но-
вом направлении уже можно выбрать не как заданную долю диапазона измене-
9

ния независимой переменной, а как заданную долю расстояния, пройденного
вдоль предыдущего направления с наибыстрейшим убыванием критерия. Это
позволит автоматически уменьшать начальный шаг по каждому следующему
направлению наибыстрейшего убывания критерия оптимизации.
В градиентном методе направление движение обуславливается величина-
ми частных производных критерия оптимизации в рассматриваемой точке. Все-
гда следует иметь ввиду, что градиент ортогонален к поверхности постоянного
уровня критерия оптимизации только в точке его вычисления, да и то с некото-
рой погрешностью, которая обусловлена многими факторами, например ис-
пользованием численных методов.
В точке
],1[
+
l
q
как результат выполнения шага от точки
][l
q
градиента
])[( lI
q
q
∇
в общем случае не ортогонален поверхности постоянного уровня кри-
терия оптимизации, проходящей через точку
].1[
+
l
q
Тем самым, градиент
])[( lI
q
q
∇
и
])1[(
+∇
lI
q
q
отличаются по направлению, что может быть исполь-
зовано в стратегии изменения величины шага; например в соответствии с пра-
вилом
>⋅
<<
<
=+
при
при
при
,][],[5,0
,][],[
,][],[2
]1[)18(
max
maxmin
min
αα
ααα
αα
llh
llh
llh
lh
где
−
][l
α
угол поворота градиента на l-ом шаге, определяемый выражением
,
])1[(])[(
])1[(])[(
][cos)19(
3
1
3
1
22
3
1
∑ ∑
∑
= =
=
∂
−∂
∂
∂
∂
−∂
∂
∂
=
j j
jj
j
jj
q
lI
q
lI
q
lI
q
lI
l
qq
qq
α
−
maxmin
,
αα
допустимые пределы угла поворота градиента.
Достоинством алгоритма изменения величины шага (19) является то, что
при его использовании возможно как увеличение, так и уменьшение величины
шага.
Рассмотрим еще одну стратегию выбора величины шага в заданном
направлении, в котором используется информация, полученная на предыдущих
шагах по этому же направлению. В основу положено то, что в процессе движе-
ния вдоль заданного направления характер изменения критерия оптимизации
аппроксимируется по результатам трех последних шагов полиномом второго
порядка.
10
