Крук Е.А. (ред.) Исследование LDPC кодов. Сборник статей. Часть 2
Подождите немного. Документ загружается.


71
Следствие 2. Пусть
1
– гладкая проективная кривая рода g над F
q
и пусть
2.k 1
Тогда расстояние линейного (n, k, d)
q
алгебро&геомет&
рического кода удовлетворяет неравенству
12.dq g q
12
3 45
67
Доказательство. Из границы Синглтона получаем
1.nkd1 23
Со&
гласно теореме 1, длина кода может быть оценена сверху как
12
12.
q
nNg nq g q
34
56577
89
Эту оценку можно уточнить, учиты&
вая, что для построения кодов с
2k 1
и d < n необходимо, что&
бы deg( ) 0D 1 (теорема 3). Это означает, что длина кода будет, по край&
ней мере, на единицу меньше количества точек на кривой. Тогда
21,qg q nkd
12
3 4435
67
откуда получим оценку
12dq kg q
12
345 4
67
и, учитывая тот факт, что 2,k 1 получим
12.dq g q
12
3 45
67
Таким образом, все приведенные теоремы дают представление о
параметрах линейного алгебро&геометрического (n, k, d)
q
&кода.
Алгеброгеометрические коды, лежащие на границе Грайсмера
Для кодов с
2k 1
рассмотрим случай с d ¹ 0 mod q. Преобразуем
равенство (1), применив формулу
1:aa1 2
34 56
5 678
11 1
01 1
1,
kk k
ii i
ii i
dd d
nddk
qq q
1 2 1 2 3 4
5565676
3 4 3 4 3 4
3 4 3 4 8 9
следовательно,
1
1
1.
k
i
i
d
ndk
q
12
3 4 5 4
12
67
8
(3)
Лемма 1. Если g удовлетворяет соотношению
1
1
,
k
i
i
d
g
q
12
3
12
4 5
6
то код
лежит на границе Грайсмера.
Доказательство. Покажем, в каком случае алгебро&геометричес&
кий код будет иметь длину не более длины, определенной границей
Грайсмера.
Длина кода, лежащего на границе Грайсмера, должна удовлетво&
рять соотношению
1
1
1.
k
i
i
d
ndk
q
12
3 4 5 4
12
67
8
(4)
С другой стороны, длина алгебро&геометрического кода ограниче&
на неравенством
1,nkd g123 2
(5)
как следует из следствия 1.
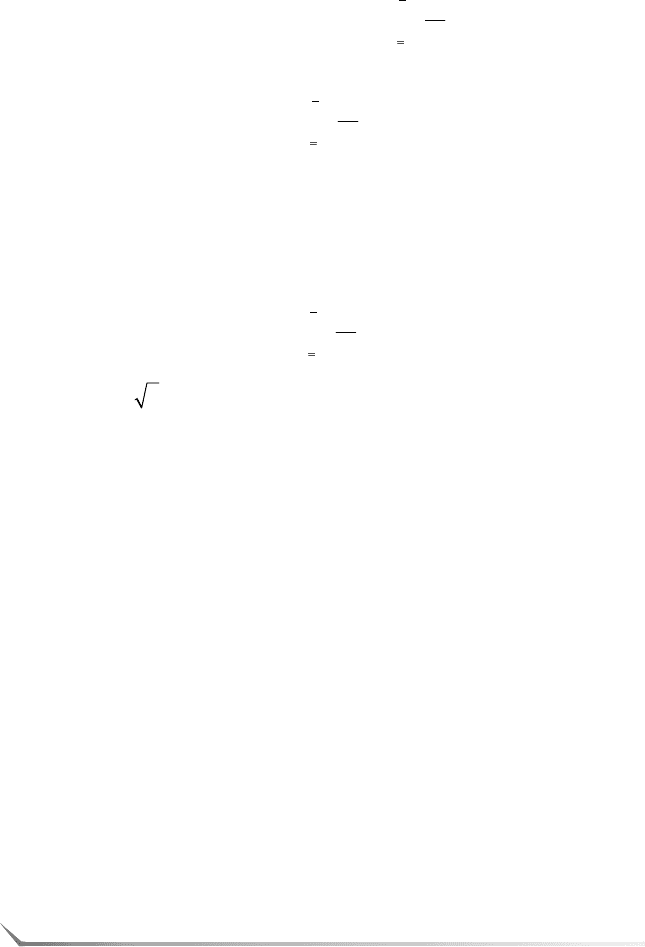
72
Тогда условие, при котором правая часть неравенства (5) оказы&
вается меньше правой части равенства (4), можно записать следую&
щим образом:
1
1
11
k
i
i
d
kd g dk
q
12
3 4 3 5 3 4 3
12
67
8
или
1
1
,
k
i
i
d
g
q
12
3
12
4 5
6
(6)
что и требовалось доказать.
Теорема 4. Любой алгебро&геометрический код с d > q и g = 1 лежит
на границе Грайсмера.
Доказательство. Воспользуемся результатом леммы 1 и докажем,
что это условие выполняется. Перепишем неравенство (6) при g = 1.
Тогда
1
1
1,
k
i
i
d
q
12
3
12
4 5
6
(7)
но
212qdq q q
12
334 5 3
67
при 2,q 1 а следовательно, правая часть не&
равенства (7) превращается в единицу, что означает выполнение ус&
ловия леммы.
Следствие 3. Параметры любого алгебро&геометрического кода с
d > q и g = 1 будут удовлетворять соотношению n = k+d.
Доказательство очевидно.
Пример. Построим поле F
16
при помощи примитивного полинома
a
4
= a + 1. Выберем кривую, например
234
.yxyx x1 2 13 13
Тогда g = 1
согласно определению 6. Найдем точки на этой кривой, лежащие в
поле F
16
.
(1,0) (a,a^3) (a^14,a^9)
(a^6,0) (a^10,a^4) (a^4,a^11)
(a^13,0) (a^11,a^4) (a^5,a^12)
(1,1) (a^14,a^4) (a^4,a^13)
(a^7,1) (a^6,a^6) (a^11,a^13)
(a^9,1) (a^9,a^7) (a^13,a^13)
(0,a^2) (a,a^9) (a^5,a^14)
(a^10,a^2) (a^7,a^9)
Построим код с k = 3 и n = 22. Тогда, согласно доказанной теореме
4 и следствию 3, данный код имеет d = 19 и будет лежать на границе

73
Грайсмера. Построим код (22, 3, 19) над F
16
, используя базис {1, x,
y}. Порождающая матрица такого кода
10 4 6 13 7 14 4 11 13 10 11 14 6 7 9 5 9
355566677 7 8 8 89101010111213
1111111111111111111111
01 1 .aa aa aaaaaaaaaa aa aaa
aaaaaaaaaaaaaaaaaaaaaa
1 2
3 4
3 4
3 4
56
Заключение
В данной работе доказано существование алгебро&геометрических
кодов рода 1, лежащих на границе Грайсмера. Поскольку основны&
ми фактами при доказательстве утверждений стали теорема 3 и тео&
рема 1, то полученные результаты справедливы для кодов, которые
построены на произвольных кривых.
Литература
1. МакВильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих
ошибки. М.: Связь, 1979.
2. Stichtenoth H. Algebraic function fields and codes. Berlin: Springer&
Verlag, 1993.
3. Влэдуц С. Г., Ногин Д. Ю., Цфасман М. А. Алгебро&геометрические
коды. Основные понятия / МЦНМО. М., 2003.
4. Виноградов И. М. Основы теории чисел. М.: Наука, 1972.

74
А. В. Афанасьева,
аспирантка
С. В. Беззатеев,
канд. техн. наук, доцент
СанктПетербургский государственный университет
аэрокосмического приборостроения
НОВЫЙ СПОСОБ ПОСТРОЕНИЯ CFF
Введение
Cover&free families (CFF) рассматривались в теории информации,
комбинаторике и групповых тестах. Впервые данный объект был вве&
ден в работе [1] в 1964 году для рассмотрения неслучайных наложен&
ных двоичных кодов. Позднее появилось множество работ, посвя&
щенных этим кодам и, соответственно, CFF. В 1985 году была опуб&
ликована статья [2], где к описанию CFF был применен комбинатор&
ный подход, и построены первые оценки для соотношения парамет&
ров схемы. А в 1987 году авторы работы [4] впервые ввели понятие
CFF и рассмотрели его применение для создания групповых тестов.
С тех пор множество работ было опубликовано по данной теме, они
относились к различным областям, применяли разные методики для
построения CFF и получения оценок для них. Многие результаты
были несколько раз «переоткрыты», а теоремы «передоказаны». Наи&
более полный обзор, обобщающий все имеющиеся результаты по дан&
ной теме, был приведен в работе [5], там же можно более подробно
ознакомиться с существующими подходами к построению CFF. Само
понятие CFF было обобщено различными способами для использова&
ния в прикладных областях. Каждое обобщение требовало измене&
ния или разработки новых способов построения, уточнения оценок и
т. п. Самое первое и наиболее узкое определение, на которое мы и
будем в дальнейшем ориентироваться, звучит следующим образом.
Определение.
Пусть
(,)X 1
– система множеств, где
1
2
12
, , ...,
v
Xxx x3
и
1
2
: 1, ..., ,
i
A
Xi N34 31
A
i
– некоторые подмножество X. Система
множеств
(, )X 1
будет r&CFF (v, N) в том случае, если для любого
подмножества
112
такого, что
,r11
и для любого
j
A 11234
верно
утверждение
l
jl
A
AA1
1
.
Иначе говоря, в r&CFF (v, N) объединение любых r блоков не по&
крывает ни одного другого блока.

75
В этой работе будет представлен новый способ построения CFF
именно в такой формулировке, поэтому не будут рассматриваться
различные обобщения, которые можно встретить в работе [5].
Способы построения CFF
В общей сложности все ранее предложенные подходы к построе&
нию CFF можно разделить на три направления: комбинаторный под&
ход, кодовую теорию и вероятностные методы.
1. Комбинаторный подход. Первым и наиболее изученным явля&
ется комбинаторный метод.
В работах [1–3] были предложены различные схемы построения
r&CFF на базе t&схем. Подробное описание этих схем мы здесь приво&
дить не будем, напомним только полученные в данных работах оцен&
ки на параметры CFF.
Используя свойства блок&схем, можно вывести следующие соот&
ношения между параметрами CFF, полученными на их основе:
2
(),vOr1
/2
().
t
NOv1
Однако существует серьезное ограничение на
использование подобных конструкций, связанное с тем, что не суще&
ствует на данный момент блок&схем с
6t 1
.
В работе [8] предложен другой подход: построение r&CFF на базе раз&
деляющих семейств хеш&функций (separating hash families). Данный
подход позволяет получить значительно более сильные результаты и не
имеет таких серьезных ограничений, как t&схемы. В работе [8] получе&
ны следующие результаты для CFF: для любого положительного r мож&
но построить r&CFF(v, N) такое, что
log( 1)
()
r
NOv1
,
2
()vOr1
.
2. Коды, исправляющие ошибки. Кодовый подход при построе&
нии CFF начал применяться несколько позднее комбинаторного, и
ему посвящено значительно меньше публикаций. В работе [2] пред&
лагалось использовать обычные и укороченные коды Рида–Соломо&
на. Еще две работы [6, 7] посвящены использованию алгебро&геомет&
рических кодов (Гоппы и Garcia&Stichtenoth) для построения CFF.
Перечислим полученные в указанных работах оценки, более подроб&
но способ построения будет раскрыт ниже в описании нашего подхо&
да к построению CFF.
Для кодов Рида–Соломона было доказано, что для r > 2 более
эффективно использовать укороченные коды. Для таких кодов дока&
зано, что
22
(log )vOr N1 . Коды Garcia&Stichtenoth уступают в эф&
фективности кодам Рида–Соломона.
3. Вероятностный подход. Вероятностный подход использовался
во многих работах как для получения теоретических границ, так и
при попытках построить конкретные схемы. Можно привести мно&

76
жество работ, где использовался этот подход, все полученные резуль&
таты были приблизительно схожи между собой. Поэтому воспользу&
емся результатами из работы [10]. В работе доказано, что для неко&
торых v, r и k, таких, что v > 2k, существует система множеств с
постоянным размером блока k и параметром t, с
2
2( 1) /kkp kt
Ne1
и
()
1
r
r
vk
p
v
1
2 1
такая, что вероятность того, что данная система не
является r&CFF(v, N), не превосходит e
–t
.
Границы CFF
В этом разделе будут представлены неконструктивные границы,
которые были доказаны, но еще не были получены примеры, удов&
летворяющие данным границам.
Первая верхняя граница для количества блоков r&CFF с постоян&
ным размером блока k была построена в работе [2] :
1
.
1
kk
rr
vk
N
1
232 3
4
565 6
565 6
78 78
1
9 9
Наилучшая нижняя оценка на размер алфавита приведена в рабо&
те [11]:
2
log ,
log
r
vc N
r
1
где с – некоторая константа. В рассматриваемой работе [2] c » 1/2, по&
зднее были получены другие оценки: c » 1/4 [12] и c » 1/8 [13].
При сравнении различных способов построения CFF можно заме&
тить, что наилучшие и ближайшие к теоретическим границам ре&
зультаты можно получить при использовании кодов, исправляющих
ошибки (таблица).
2
log
log
r
cN
r
FFCяинеортсопыдотеМативафларемзаР v
:дохдопйынротанибмоK
хамехс&колбан
O(N ,) N > r
2
хакиньлогуомярпихатардавкхиксниталан
O( rN
2
)
дохдопйыводоK
O(r
2
gol N)
ацинаргяаксечитероеТ
Сводная таблица границ для CFF

77
Таким образом, остается только подобрать наиболее подходящий
тип кодов, позволяющий строить оптимальные CFF.
Предлагаемая схема использования кодов для построения CFF
Пусть C – некоторый (n, M, d)
q
&код, где n – длина кодового слова;
M – количество слов в коде; d – расстояние кода; q – поле, над кото&
рым построен код. Тогда можно построить r&CFF (nq, M), где
1n
r
nd
1
2
1
[3]. Блоки CFF строятся из слов кода, каждому слову ставится в соот&
ветствие блок. Блоки формируют пары
12
,
i
i 3
, где i – это номер пози&
ции кодового слова; а
i
1 – элемент, стоящий на этой позиции. Таким
образом, длина блока равна n – длине кодового слова, а размер алфави&
та, составленного из всех возможных пар
12
34
,:1, , 0, 1,iin q56 56 7
соответственно равен
qn1
.
Чтобы получить оптимальную схему CFF, нам надо построить схе&
му с минимальным размером алфавита при максимальном числе бло&
ков и максимальной величине r. Для этого необходимо найти код с
максимальным d при минимальном nq, для минимизации размера
алфавита. Данное соотношение достижимо для кодов, лежащих на
границе Синглтона [2, 7]. И естественно, что данные коды давали
наилучшие результаты среди кодовых подходов. Однако из таких
кодов известны только коды Рида–Соломона, у которых длина не
превосходит размера поля. Это приводит к серьезному ограничению:
нельзя на небольших полях построить схемы CFF с произвольным r.
Размер поля существенно ограничивает наши возможности.
Так как
nq1
, то можно записать
;nqs1 2
() 1.rn d n1 2 1
Согласно границе Синглтона:
1,ndk123
поэтому
(1)1;rk d d n122 32 (1)1;rk n123
(1)1;qsrk1 2 1 3
1.qsrkr1 213
Так как число блоков CFF совпадает с количеством кодовых слов, то
N = M = q
k
,
следовательно:
2
2
log
log ;
log
q
N
rk r N r
q
11
2
2
log
log 1 1;
log
q
N
qsr Nr r r
q
1 2 1 32 1 3

78
22 2
log log ( 1)log .qqrNrs q1 223
Если
1sr1 2
, то
22
log log ,qqrN1
иначе, если
01sr123
, то
22 2
log log log .qqrNrq1 2
Эти соотношения ограничивают величины r и N сверху при за&
данном q, что не позволяет построить на определенном поле лю&
бую схему.
Следовательно, для того чтобы добиться выигрыша, необходимо
перейти к другому классу кодов, близкому по соотношению парамет&
ров и не имеющему таких ограничений на длину. Это позволит при
меньших значениях поля получить большие длины кодов и расстоя&
ния, а следовательно, уменьшить алфавит при прочих равных значе&
ниях.
Коды на границе Грайсмера
Граница Грайсмера является верхней границей для параметров
кодов, следовательно, коды, лежащие на данной границе, имеют
минимальную длину при заданных значениях d, k, q. Некоторые из
кодов на границе Грайсмера не удавалось построить, для других до&
казано, что они не существуют, но если рассматривать существую&
щие коды на границе Грайсмера, они имеют оптимальные парамет&
ры, по сравнению с любыми другими кодами.
Граница Грайсмера [14] уточняет границу Синглтона и выражает&
ся следующей формулой:
1
0
,
k
i
i
d
n
q
1 2
3
45
45
6
где n – длина кода; k – размерность кода; d – расстояние кода; q –
размер поля, над которым задан код. Для кодов, лежащих на грани&
це Грайсмера, выполняется равенство, таких кодов известно доста&
точно много, и существуют конструктивные способы их построения
[15–18]. Так, существуют алгебро&геометрические коды, построен&
ные на эллиптических кривых, лежащие на этой границе. Легко по&
казать, что при 0 dq11граница Грайсмера совпадает с границей
Синглтона.
Таким образом, при построении CFF на кодах, лежащих на грани&
це Грайсмера, можно получить лучшие значения параметров по срав&
нению с уже существующими способами построения.
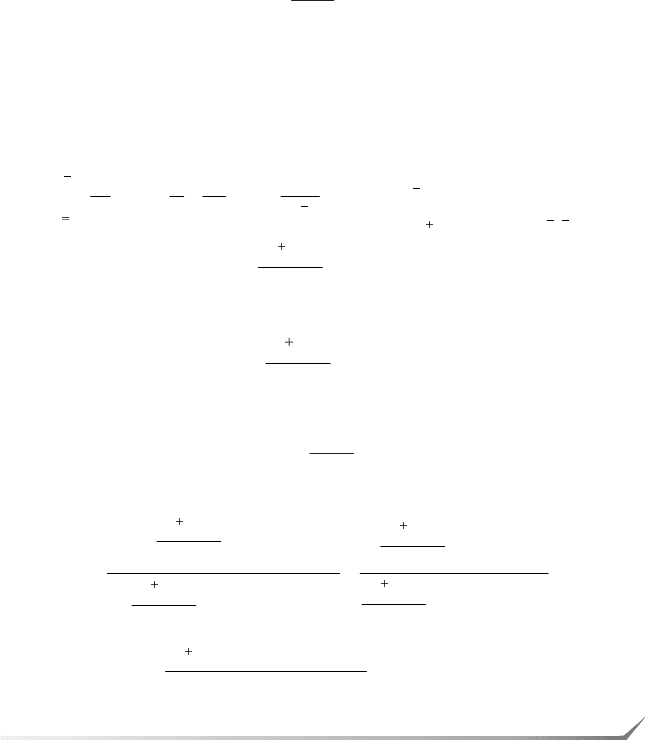
79
Полученные результаты
Еще раз напомним все введенные ранее обозначения, которыми и
воспользуемся для сравнения полученных нами результатов с уже су&
ществующими схемами: v – размер алфавита CFF; r – количество бло&
ков, не покрывающих больше ни один блок; N – количество блоков; q –
размер поля, на котором построен код; d – расстояние кода; n – длина
кодового слова; k – размерность кода; c, a – произвольные константы;
z – произвольная целочисленная константа.
Теоретическая граница на размер алфавита (v), приведенная в ра&
боте [11], связывает эти параметры:
2
log .
log
r
vc N
r
1
Теорема 1. Для получения оптимальных параметров CFF с ис&
пользованием кодов, лежащих на границе Грайсмера, необходимо
выбирать коды с d < q
2
.
Доказательство.
Пусть d = aq
z
(z < k и a < q), тогда
1
1
21
0
1
1
1
... ( ... 1 1 ... 1)
1
1.
1
k
zz
ik
i
kz
z
z
ddd d
nd bqqq
q
qqq
q
akz
q
1 2
3344 4 4 3 4 4 444 4 3
56
56
78
9
3 4 99
9
123 24
12223 2 2 24
Таким образом:
1
1
1.
1
z
q
na k z
q
12
3
4533
67
67
3
8 9
Для любых кодовых конструкций СFF известно:
1
,
n
r
nd
1
2
1
отсюда
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
для .
z
z
z
z
z
z
z
z
q
q
akz
kz
q
q
r
q
q
kzq
akzaq
q
q
qzqzkqkq
qkq
qzqzkqkq
12
3
3
433
56
433
56
3
3
78
999
12
3
3
4333
433 3
56
56
3
3
78
34433
9
34433

80
Размер алфавита CFF
1
112
1
1
1
(...()),.
z
zzz
q
vnqa zk q
q
aq q q q qk z z k q
12
3
44 3 5 3 4
6 7
6 7
3
89
4 55 555 3
Следовательно, чтобы рост размера алфавита от количества под&
писей не превосходил O(r
2
logN), необходимо, чтобы
1z 1
, т. е.
2
daqq1 2
.
Как уже упоминалось, при d < q мы получаем обычный МДС&код и
результаты, уже известные для кодов Рида–Соломона. Поэтому имеет
смысл рассматривать только коды, у которых q < d < q
2
, то есть d = aq,
где 1 < a < q – некоторая константа.
Теорема 2. Оптимальные параметры CFF, построенных на кодах,
лежащих на границе Грайсмера, можно получить при использова&
нии кода с d = (k–2)q.
Доказательство.
Пусть d = aq (1 < a < q), тогда
1
21
0
... 2;
k
ik
i
ddd d
nd aqak
q
qqq
1 2
3344 4 4 3 445
6 7
6 7
8
2.naqak1 223
Следовательно:
13
;
2
naqak
r
nd ak
1 221
33
1 2 1
23;ar kr r aq a k123112
2 3 (1)(2)(2)1
(1)(1)(2)1(1)( 2)1(1)( 2)
,
ar kr r a k a r r k k
q
aa
ar r k r a k r a k
aaa
12221 21 2221
33 3
2 1 2 2 1 2 12 1 2 12
334
а размер алфавита
121212
12
121 2
12
121 2
2
12
212(2)
12
(2)
2(1).
rak
vnq aqak q r ak ak
a
rak
ak
ra k rr
aa
343
55 443 63 43443 5
343
43
543 53
Для получения оптимальных параметров CFF необходимо мини&
мизировать размер алфавита, попытаемся найти экстремум получен&
ной функции размера алфавита от переменной a:
