Крук Е.А. (ред.) Исследование LDPC кодов. Сборник статей. Часть 2

Подождите немного. Документ загружается.

k элементов для восстановления всего кодового слова. В результате вме&

сто n точек будет храниться k, а сжатие составит n/k раз. Потери каче&

ства будут происходить из&за того, что при замене реальных доменов на

кодовые слова идеального соответствия не будет. Главным достоинством

при этом является то, что сам код в этом случае вообще не передается.

Данный метод для случая использования кодов Рида–Соломона опи&

сан в [11].

С точки зрения сжатия и последующего восстановления, радиус по&

лученного покрытия для изображения влияет на качество восстанов&

ленного изображения: чем больше радиус, тем хуже объективное каче&

ство. На радиус покрытия будут влиять как количество слов в коде G,

так и расположение этих слов в пространстве относительно точек по&

крываемого множества, следовательно, чем лучше выбран код, тем луч&

ше будет качество восстановленного изображения. Если использовать

линейный (n, k)&код, то его можно компактно хранить, например, в виде

генераторной матрицы кода. Тогда для квантования различных изоб&

ражений можно использовать разные коды и, следовательно, несколь&

ко улучшить качество.

Однако, даже несмотря на то, что при использовании помехоустой&

чивого кода для квантования изображений сам код не нужно хранить,

общее сжатие оказывается значительно меньшим по сравнению со сжа&

тием при адаптивном построении кода. Дело в том, что адаптивное по&

строение позволяет построить код существенно меньшей размерности

при одинаковом качестве восстановленных изображений. Следователь&

но, все равно необходим путь адаптации кода к изображению.

Адаптация изображения к коду

Пусть есть некое пространство C и некий код W, полностью по&

крывающий пространство C радиусом R. Это означает, что для любой

точки пространства C найдется кодовое слово кода W, расстояние от

которого до точки пространства не превышает R:

: , ( , ) ,wW cCdcw R12 32 4

где

(, ) ( ).

dc w w c12

Пусть C¢ – пространство, точками которого являются реальные

домены изображения, и пусть есть набор обратимых преобразований

M, определенный над множеством точек пространства C¢ так, что ре&

зультат преобразований из M всегда принадлежит пространству C:

, : ,cCmMcmc

11 1

2 33 4

c Î C.

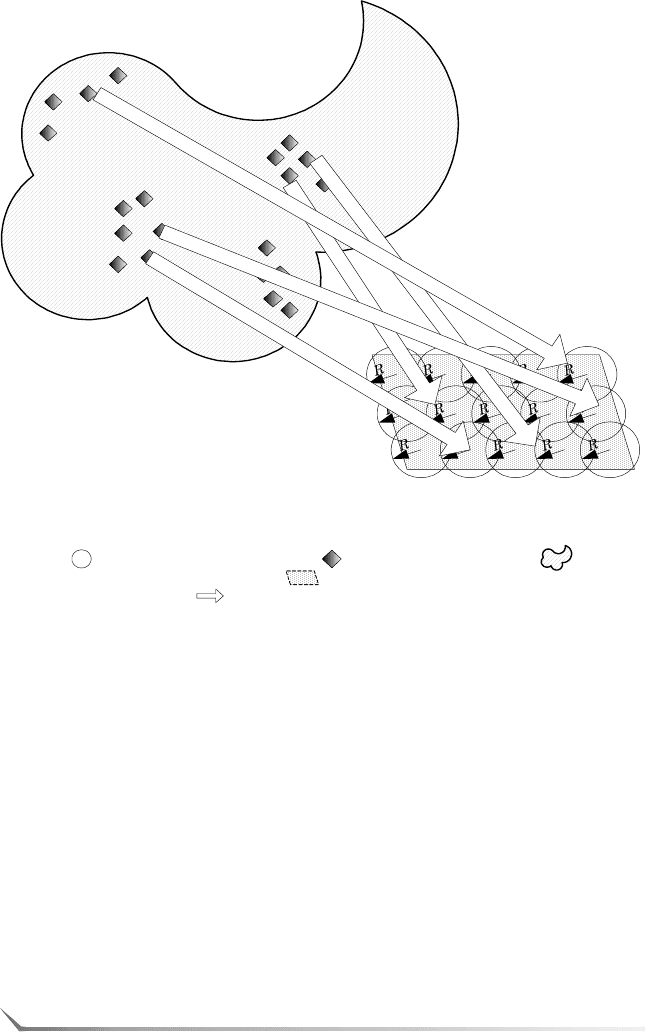
Таким образом, любую точку из пространства C¢ можно при помощи

преобразований из M перевести в точку пространства C, где она будет

покрыта кодом W с радиусом R, следовательно, использование кодово&

го слова из W в качестве квантователя для точек вида mc¢, c¢ Î C¢ не

будет давать ошибку квантования больше, чем R, и преобразования

смогут подстроить единый код под конкретное изображение (рис. 3).

Использование свойств кодов, исправляющих ошибки,

в квантовании

При квантовании точек пространства возникает задача поиска

ближайшего кодового слова для произвольной точки пространства.

В общем случае эта задача может быть решена полным перебором

всех кодовых слов. Но, исходя из допущения, что код, покрываю&

щий пространство, обладает некими свойствами, по аналогии с по&

мехоустойчивым кодированием, можно рассматривать произвольную

точку пространства c как некое кодовое слово a с добавленным векто&

ром ошибки e:

a = c+e, c Î C.

Рис. 3. Использование преобразований для перехода к другому

пространству:

– кодовое слово из базиса; – домен изображения; –

исходное пространство; – пространство, полностью покры

тое кодом W; – преобразование

Будем называть весом ошибки расстояние от точки, соответству&

ющей вектору ошибки, до нулевого вектора (вектора, элементами

которого являются нули):

() (,0).wt e d e1

Тогда задачу поиска кодового слова, находящегося на расстоянии

не больше чем R от заданной точки, можно свести к задаче поиска

вектора ошибки минимального веса: по принятому вектору a нужно

найти такой вектор ошибки e, вес которого не превышал бы R, кото&

рый в сумме с кодовым словом давал бы принятый вектор:

:, ,().ea w ew Wwte R1 2 3 4

В терминах помехоустойчивого кодирования эта задача может быть

описана как задача декодирования кода W в радиусе до R, то есть

поиска такого кодового слова w Î W, что , ( ) .wcewte R1 2 3

Теперь общий принцип сжатия изображений при помощи помехо&

устойчивых кодов можно сформулировать так:

– каждый домен x

изображения отображается при помощи преоб&

разований в точку c

пространства C, покрытого кодом W;

– в пространстве C выполняется декодирование вектора c

в коде

W, т. е. находится ближайшее кодовое слово w

, принадлежащее коду

W, и это слово w

считается квантователем для исходного домена x

;

– сохраняется g

– информационная совокупность слова w

. Сжа&

тие от квантования будет состоять в том, что вместо домена x

будет

храниться информационная совокупность g

Однако подстройка изображения под код может быть выполнена не

только за счет преобразований. Существует метод, подстраивающий

изображение под фиксированный помехоустойчивый код за счет согла&

сованной потери качества, работающий следующим образом. Из доме&

нов изображения последовательно формируются двоичные битовые

плоскости, а затем каждая битовая плоскость квантуется при помощи

декодирования заданного двоичного кода с низкой плотностью прове&

рок на четность. Таким образом, в качестве преобразований, переводя&

щих домены в другое пространство, метод использует разбиение доме&

нов на битовые плоскости, а в качестве покрывающих кодов использу&

ются двоичные коды с низкой плотностью проверок на четность.

Основная идея данного метода состоит в том, что при квантовании

компоненты битовых плоскостей имеют различную значимость для вос&

становленного изображения. Пусть необходимо проквантовать самую

старшую битовую плоскость (плоскость, состоящую из старших битов

элементов доменов). Очевидно, что ошибки квантования этой плоско&

сти приведут к самым большим ошибкам в восстановленном изображе&

нии, однако, следует принять во внимание факт, что далее будет произ&

водиться квантование остальных битовых плоскостей, и некоторые

ошибки квантования старшей плоскости могут быть учтены при кван&

товании младших битовых плоскостей.

Рассмотрим пример. Значения яркости доменов разбиты на 8 бито&

вых плоскостей:

{ , ...}.

iii

Xxx1

Пусть в старшую битовую плоскость

попадают два значения

x , оба равные единице:

соответствует

единице в старшем разряде яркостной компоненты X

, равной 255, а

x –

единице в старшем бите от числа X

= 128. Ошибки квантования обоих

бит приведут к одинаковой ошибке квантования изображения, однако

ошибка квантования бита

при квантовании значений бит осталь&

ных битовых плоскостей, соответствующих X

, может только увели&

читься. При этом ошибка квантования бита

x может быть компенси&

рована при квантовании последующих уровней вплоть до единичной

ошибки, если все последующие биты плоскостей, соответствующих

компоненте X

, будут проквантованы в единичные биты. Тогда восста&

новленное значение компоненты, соответствующей X

, будет равно 127

вместо 128, что будет не различимо человеческим глазом.

Приведенный пример означает, что при квантовании необходимо

учесть значимость битов

x при использовании в качестве процеду&

ры поиска квантователя декодера, то есть какие&то биты при квантова&

нии могут допустить ошибку, а какие&то – ни в коем случае не должны.

Этого можно добиться, если выставить битам надежности, а затем де&

кодирование производить с учетом надежностей. Для этого были вы&

браны коды с некой плотностью проверок на четность, обладающие про&

стыми схемами декодирования в полунепрерывном канале, то есть схе&

мой декодирования с учетом надежностей символов. Применительно к

изображениям алгоритм декодирования используется следующим об&

разом.

Пусть {X

} – яркостные компоненты изображения, которые будут

подвергаться квантованию, {}, 1

WiN11 – коды с низкой плотнос&

тью проверок на четность, N – число бит, требуемых для двоичного

представления числа {X

}. Будем называть уровнями квантования

поиск квантователей для отдельных битов, из которых потом будут

восстанавливаться яркостные компоненты

{}.

Число уровней кван&

тования также будет равно N. Тогда алгоритм квантования с выс&

тавлением надежностей будет работать следующим образом.

1. На первом уровне квантования формируется множество бит

{}

где

– старшие биты чисел X

, и множество надежностей битов

{}

Надежности битам выставляются с учетом исходных значений X

по

формуле

1112

(2 )

ii i

lX x12 3

. Из пар

(, )

формируются векторы, яв&

ляющиеся входными данными для декодера кода с низкой плотностью

проверок на четность, а затем производится декодирование по надежно&

стям в коде W

, результатами которого являются векторы битов

2. На каждом последующем уровне квантования k,

2 kN11

, вы&

числяются разности

kNm

rX x12

, формируется множество

бит

{}

, где

1, 2 ;

0, 2 ,

kNk

и выставляются надежности этим би&

там

(2 )

kkNkk

ii i

lr x12 3 . Из пар

(, )

аналогично формируются век&

торы, являющиеся входными данными для декодера по надежнос&

тям, а затем производится декодирование по надежностям в коде W

результатами которого являются векторы битов

После прохождения всех N уровней будут получены проквантован&

ные значения

, которые будут считаться составляющими битовых

плоскостей изображения. Так как коды W

являются линейными кода&

ми, то для восстановления всего кодового слова

{ , ..., }

ww w1 необ&

ходимо знать только информационную совокупность слова c. При ис&

пользовании на уровнях квантования кодов с низкой плотностью про&

верок на четность длиной n

и числом информационных символов k

сжатие только за счет квантования составит

раз. Так как

коды являются алгебраическими структурами, то хранить коды можно

компактно, а так как коды остаются неизменными для всех изображе&

ний, то никакой информации о кодах не будет записываться в сжатый

поток.

Квантование изображений LDPCкодами

В общем случае для процедуры квантования, описанной выше, мож&

но брать произвольные коды, имеющие схему декодирования с исполь&

зованием надежностей. Одним классом кодов с такими свойствами яв&

ляются коды с низкой плотностью проверок на четность [12] или LDPC&

коды. Данные коды являются линейными блоковыми кодами, облада&

ют простой схемой декодирования по надежностям, и, следовательно,

могут быть использованы для сжатия изображения описанным мето&

дом.

Очевидно, что использование одного и того же кода на всех уров&

нях квантования хороших результатов не даст ввиду того, что, как

уже упоминалось, ошибки на каждом уровне квантования по&разно&

му влияют на общую ошибку квантования, следовательно, этот факт

должен быть как&то учтен при выборе кодов.

Наиболее простым представляется последовательное увеличение

избыточности (или, что то же самое, уменьшение скорости) кодов,

которые используются на уровнях квантования:

...

и т. д.

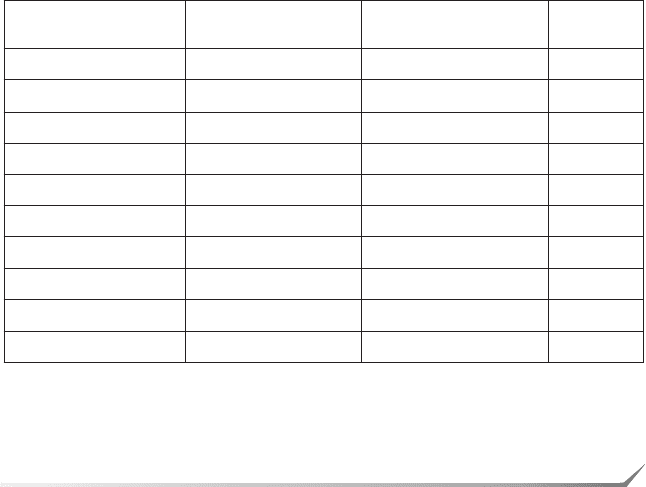
Результат применения описанного кодового квантования битовых

плоскостей с использованием надежностей к тестовому изображению

«LENA» приведен на рис. 4. Использованы LDPC&коды (16, 8),

(16, 8), (16, 8), (16, 8), (64, 14), (256, 29), (256, 29), (256, 29).

Заключение

Рассмотренный метод кодового квантования изображений дает

неодинаковые результаты на различных типах доменов, но есть типы

доменов, на которых качество восстановленных изображений пре&

восходит качество восстановленных доменов при использовании алго&

ритма JPEG. Так как кодовое квантование битовых плоскостей с выс&

тавлением надежностей в работе оперирует доменами изображения, есть

Рис. 4. Восстановленное изображение при использовании кодового

квантования (SNR = 23.61 дБ, PSNR = 30.25 дБ)

возможность использовать его совместно с каким&либо иным алгорит&

мом сжатия, использующим разбиение изображения на домены, напри&

мер алгоритмом JPEG, так, чтобы для каждого домена изображения

всегда использовался метод, дающий лучшие результаты на данном

домене. Принцип совместного использования может быть следующим:

– фиксируется минимально допустимое качество восстановленно&

го изображения;

– все домены изображения сжимаются при помощи кодового кван&

тования, а затем разности между исходными доменами и восстанов&

ленными после кодового квантования кодируются дополнительно

алгоритмом JPEG для кодирования разностей для обеспечения за&

данного качества;

– в случае, если кодовое квантование с последующим кодирова&

нием разности алгоритмом JPEG дает большее количество байт,

чем традиционный алгоритм JPEG с заданным качеством, данный

домен кодируется традиционным алгоритмом JPEG.

При описанном принципе использования кодового квантования

совместно с алгоритмом JPEG для сжатия изображений, представ&

ляющих собой 256 оттенков серого, и обеспечения высокого каче&

ства восстановленных изображений в среднем на 11 % доменов на&

блюдались выигрыши от использования кодового квантования. Под&

робные данные приведены в таблице.

еовотсеТ

еинежарбози

,вонемодтнецорП

шыргиывхищюад

умещбоопшыргиыВ

тйаб,юитажс

RNS

pmb.enalpria_g73,400552.73

pmb.erahcitcra_g70,0048.14

pmb.noobab_g01,150056120.33

pmb.arabrab_g27,41000324.33

pmb.tao

b_g00,12000483.33

pmb.tac_g52,01008153.53

pmb.stiurf_g38,400892.53

pmb.anel_g72,500891.23

pmb.sreppep_g25,400898.23

pmb.l

oop_g67,0069.03

Описанная схема может применяться в приложениях, требующих

высокого качества восстановленных изображений, например коди&

рование фильмов для записи DVD или спутниковое телевидение.

Литература

1. Gray R. M. Fundamentals of Vector Quantization. http://www&

isl.stanford.edu/~gray/compression.html

2. Li J., Gray R. M., Olshen R. Joint Image Compression and Classification

with Vector Quantization and Two Dimentional Hidden Markov Model // Data

Compression Conference: IEEE Computer Society TCC. 1999. P. 23–32.

3. Hung A. C., Tsern E. K., Meng T. H. Error&resilient pyramid vector

quantization for image compression // IEEE Trans. on Image. Process. Oct.

1998. Vol. 7. P. 1373–1386.

4. Lin J.H., Vitter J. S. Nearly Optimal Vector Quantization via Linear

Programming // Data Compression Conference: IEEE Computer Society TCC.

1992. P. 22–31.

5. Using vector quantization for image processing / P. C. Cosman, K. L. Oehler,

E. A. M. Riskin et al. // Proc. of the IEEE. Sept. 1993. Vol. 81. N 9. P. 1326–1341.

6. Bayazit U., Pearlman W. A. Variable&Length Constrained Storage Tree&

Structured Vector Quantization // IEEE Trans. Image Processing. Mar. 1999.

Vol. 8. N 3. P. 321–331.

7. Bradley J. N., Brislawn C. M. Wavelet transform&vector quantization

compression of supercomputer ocean models // Data Compression Conference.

May 1993. P. 224–233.

8. Raffy P., Antonini M., Barlaud M. Distortion&Rate Models for Entropy&

Coded Lattice Vector Quantization // IEEE Transactions on Image Processing.

2000. Vol. 9. N 12. P. 2006–2017.

9. Garey M. R., Johnson D. S., Witsenhausen H. S. The complexity of the

generalized Lloyd&Max problem // IEEE Trans. Inform. Theory. 1982. Vol. 28.

N 2. P. 255–256.

10. Gersho A., Gray R. M. Vector quantization and signal compression.

Kluwer Academic Publishers. Jan. 1992. 732 p.

11. Белоголовый А. В. Применение кодов, исправляющих ошибки, для

сжатия видеоизображений // Вторая Междунар. молодежная школа&се&

минар БИКАМП’99: Тез. докл. СПб., 1999. С. 119.

12. Gallager R. G. Low&density parity&check codes // IEEE Trans. on Inform.

Theory. Jan. 1968. Vol. IT&8. P. 21–28.

С. В. Беззатеев,

канд. техн. наук, доцент

М. В. Степанов,

аспирант

СанктПетербургский государственный университет

аэрокосмического приборостроения

АЛГЕБРОГЕОМЕТРИЧЕСКИЕ КОДЫ

НА ГРАНИЦЕ ГРАЙСМЕРА

Граница Грайсмера и ее связь с границей Синглтона

Рассмотрим (n, k, d)

&коды, которые удовлетворяют верхним гра&

ницам существования кодов, исправляющих ошибки [1], а именно

границам Грайсмера и границам Синглтона. Покажем связь между

этими границами.

Стандартный вид границы Грайсмера задается следующей форму&

лой:

1 2

(1)

где q – размер конечного поля F

, над которым задан код. Округление

до ближайшего целого, большего a. Коды, удовлетворяющие равен&

ству (1), будем называть кодами Грайсмера. Граница Синглтона за&

дана формулой

n = k+d–1. (2)

При q > d равенство (1) эквивалентно (2), т. е. граница Синглтона –

частный случай границы Грайсмера. Известен только один класс ли&

нейных кодов, удовлетворяющих условию (2), – это коды МДР [1].

Необходимые сведения из алгебраической геометрии

Прежде всего, рассмотрим необходимые результаты алгебраичес&

кой геометрии. К числу этих результатов отнесем границу, дающую

верхнюю оценку количества точек на алгебраической кривой, а так&

же теорему Римана–Роха, дающую оценку размерности пространства

функций, заданных на некотором дивизоре.

Сначала дадим ряд определений. Для простоты изложения все

определения, последующие ниже, будут справедливы только для глад&

ких неприводимых плоских кривых.

Определение 1. Кривой назовем полиномиальную функцию

Определение 2. Точкой на кривой назовем P = (x, y), удовлетворя&

ющую () 0,P1 2 где

, .

xy F1

Определение 3. Гладкая кривая – это кривая

у которой нет осо&

бых точек, т. е. не существует точки P:

() () () 0.

PPP1 21 21 2

Будем рассматривать только гладкие кривые.

Определение 4. Дивизор D – это формальная сумма точек кри&

вой:

Z1 2 Степень дивизора гладкой кривой deg(D) =

Рассмотрим поле рациональных алгебраических функций, в ко&

тором каждая функция может быть представлена в виде

где

g, h – полиномиальные функции, обращающиеся в нуль только в точ&

ках, лежащих на кривой. Множество таких функций будет полем

функций, заданных на кривой [3].

Нулями рациональной функции назовем точки, в которых функ&

ция обращается в нуль, а полюсами функции – точки, в которых

функция обращается в бесконечность.

Определение 5. Пространство функций, заданное на дивизоре L(D), –

это такое множество функций, в котором любая функция имеет по&

люс в тех же точках, что и дивизор D, и кратность конкретной точки

меньше или равна коэффициенту

Количество нулей функции в каж&

дой точке кривой должно быть больше или равно коэффициенту .

Определение 6 [3, следствие 2.2.8]. Род гладкой, неприводимой,

плоской кривой g определяется величиной

(1)(2)

где t – сте&

пень гладкой кривой

Теорема 1 [3, 3.1.7]. Обозначим N

(g) максимальное количество

точек на кривой. Тогда

() 1 2 .

Ng q g q

344

Теорема 2 [3, теорема Римана–Роха]. Пусть

– гладкая кри&

вая рода g, определенная над F

, и пусть D – дивизор на кривой

Тогда dim ( ) deg( ) 1 .LD D g1 23

Теорема Римана–Роха позволяет оценить базис векторов линей&

ного пространства функций, заданных на дивизоре кривой

Теорема 3 [3, теорема 4.1.1]. Пусть

– кривая рода g, определен&

ная над F

. Пусть

()

PF12

– подмножество n различных F

– рацио&

нальных точек на

и пусть D – дивизор на

0deg()Dn1 2

.PD1 2 3

Тогда алгебро&геометрический линейный код C : =

(, , )CPD1 2 длины n будет кодом c deg( ) 1kDg1 2 3 и deg( ).dn D1 2

Следствие 1 [3, замечание 4.1.10]. Алгебро&геометрические

(n, k, d)

&коды удовлетворяют соотношению 1.kdn g1213

Учитывая приведенный результат и оценку для верхней границы

длины кода N

(q), можно сформулировать следующее следствие.