Козлов В.Н. Системный анализ и принятие решений
Подождите немного. Документ загружается.


решение как функцию параметра. Это решение имеет вид:
.)(1(
~
)(
100
bAAAbPcPcPX
TTA −∗
=−−= ,
~
),
2
1
00
bPcPcP
A
+=
λ
λ
Квадратное уравнение для множителя Лагранжа
λ
имеет вид:
я
.0
~
,04)(4,0
0212
>=>+==−
−
cPcrbAAb
ТТТ
βαβαλ
−
λ
+
Из полученного уравнения можно найти два значени и
λ
, одно
из которых соответствует максимуму, а другое - минимуму
()
/ 21
∓
линейного функционала, причем результате
оптимальное решение имеет вид
Таким образом, полученное решение определяет минимум
инейного функционала на компактном множестве.
о но
:
./
αβλ
∓=
В
*1/2*
.zQxd
−
=
+
л
2. Второй вариант условной минимизации. П ста вка и
решение задачи рассматриваются в следующем виде: вычислить
вектор
x
*
=
arg min
ϕ
x
=
c
T
x
|
Ax
=
b
,||
x
||
2
≤
r
2
(5)
ля минимизации линейного функционала при ограничениях типа
равен
д
ств и квадратичных неравенств, где
mn
A
R
×
∈
.
Преобразуем задачу (5), переходя в ограничениях от
квадратичных неравенств к квадратичным равенствам. В результате
задача (5) преобразуется к следующему виду: вычислить вектор
x
*
= arg min
ϕ
x =c
T
x | Ax =b ,||x||
2
= r
2
⋅
(6)
Тогда решение задачи формулируется с помощью метода
множителей Лагранжа, а функция Лагранжа примет вид:
81
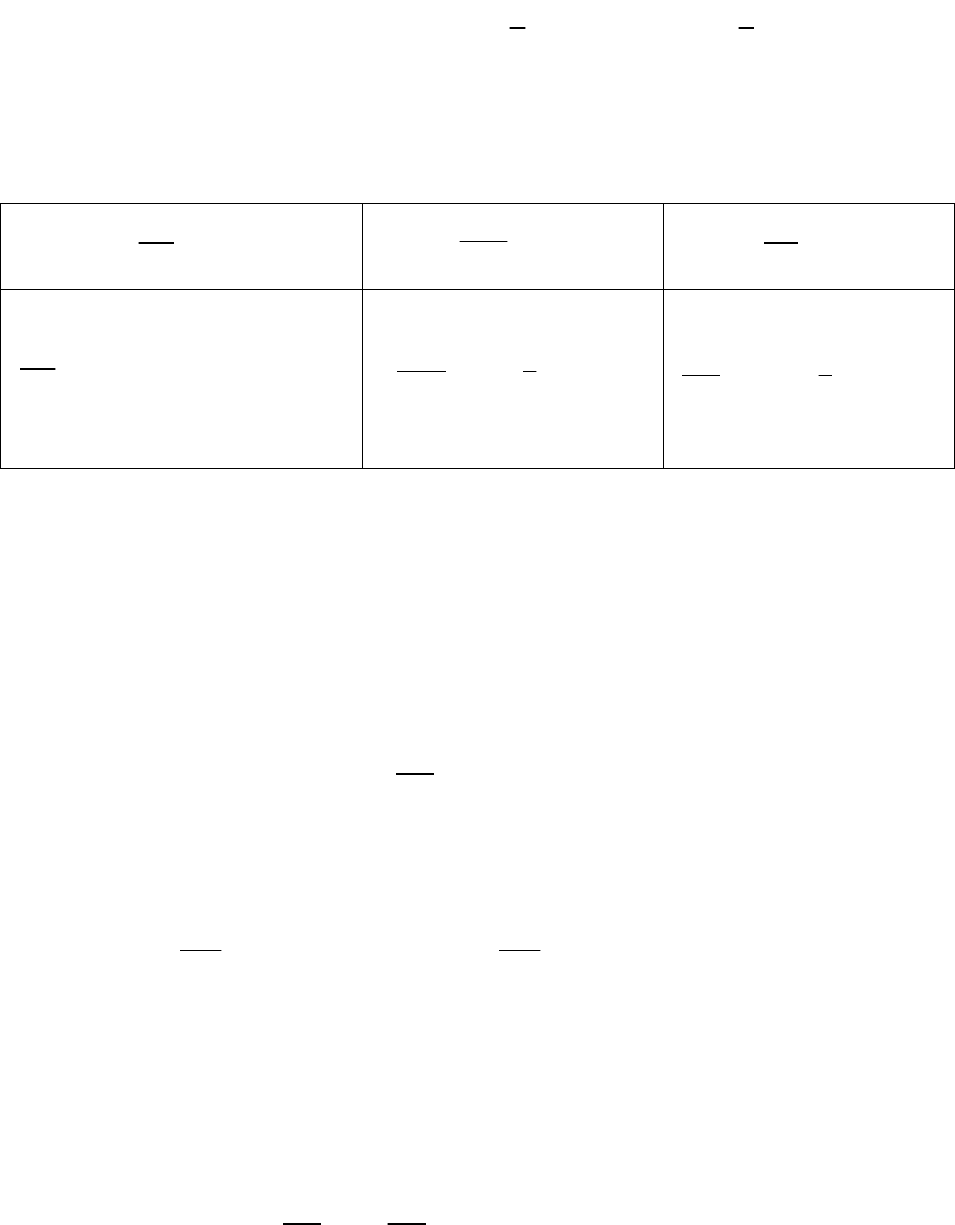
L = c
T
x
λ
0
T
()Ax b +
λ
)
||x || r
2
(
2
+
⋅
(7)
В силу метода Лагранжа необходимые условия оптимальности
можно представить следующей таблицей:
∂
L
∂λ
∂
L
∂
L
=0
=0
=0
∂
x
∂λ
0
∂
L
∂λ
0
=
Ax b
=0
∂
L
∂λ
=||
x
||
2
r
2
=0
∂
L
=
cA
T
λ
+ 2
λ
x
+ = 0
∂
x
0
(1)
(2)
(3)
Далее необходимо определить решение системы уравнений,
сформулированных в таблице. Решение может быть получено
специальными методами. Например, из уравнения (5) таблицы
определить вектор
x
можно как функцию двух множителей
Лагранжа. В результате ве ор:
кт
()
0
A
1
.
2
T
xc
λ
λ
(8)
Из (8
=− +
) и условия (2) таблицы следует равенство:
() ()
00
11
0.
22
TT
A c A b Ac AA b
λλ
λ
λ
−+−=−+−=
(9)
Если матрица
T
A
A
неособенна
A
я (строки матрицы – линейно
независимые), то можно из (9) получить линейное алгебраическое
уравн
ение:
0
11
0.
T
Ac AA b
λ
−− −=
22
λλ
(10.а)
В результате вектор множителей Лагранжа λ
0
примет вид:
].
1
0
()[2
T
A
AbA
λλ
−
=− + c
(10.б)
82

Если подставить .б) в (9), то можно получить уравнение:
(10
cA
T
()
AA
T 1
[]2
λ
bAc + 2
λ
x + = 0
⋅
(11.а)
Система (11.а) – линейная алгебраическая система,
разре сительно вектора
x
шаемая отно . Тогда ктове р
x
как функция
множ теля Лагранжа определяется из условия
m
R
λ
∈
: и
cA
T T 1
()
AA A
()
AA
T T 1
2
λ
b Ac 2
λ
x + = 0
⋅
Тогда можно преобразовать последнее уравнение к виду
[]
EA
T
()
AA
T 1
A cA
T
()
AA
T 1
2
λ
b
2
λ
x
+ = 0
⋅
(11.б)
Далее :
В результате вектор уравнения (11.б) примут вид:
будут использованы обозначения
01
()
TT
PEAAA A
−
=−
,
1
()
TT
AAAA
−
−
=
.
0
22Pc A b x
λλ
−+=
0.
(11.в)
После этого вектор
x
можно определить равенством:
0
1
2.
2
x
Pc A b
λ
λ
⎡
⎤
=−+
⎣
⎦
(12)
Далее после подстановки (12) в квадратичное ограничение типа
равен ожно получить уравне :
ств в (6) м ние
||x||
2
r
2
= x
T
xr
2
,
1
(),
2
xae
λ
λ
=+
ричем
0
aPc=−
,
2eAb=
. Послегде п подстановки
полученного вектора в квадратичное ограничение типа равенств
зад уравнение
−
ачи (6) можно получить
83

22
1
[][]
TT
xx r a e a e r
λλ
−= + + −=
2
4
λ
(13)
2
2
1
[][]
4
TT
aeaer
λλ
λ
=++−
0.=
нение (13) уравнеУрав это квадратное ние относительно
неизвестного скалярного множителя Лагранжа
λ
∈
R
1
ельно принимает вид:
, которое в
результате преобразований последоват
[]
a
T
λ
e
T
+ [ ]
a
λ
e
+ 4
λ
2
r
2
=0
, (14)
a
T
a 2
λ
e
T
a +
λ
2
e
T
e + 4
λ
2
r
2
=0
, (15)
поскольку:
a
T
b
=
b
T
a
.
Уравнения (13)-(15) – алгебраические уравнения относительно
(1 чтскалярного множителя Лагранжа λ. Из 5) следует, о
λ
=
λ
1
*
и
λ
=
λ
2
*
.
(16)
Эти решения квадратного алгебраического уравнения обладают
свойс дно из них соответствует миним
а другое – максимуму. Этот вывод следует из геометрической
интер задачи. В результате оптимальн решение
равенство (12) с параметрами, вычисляемыми как
реше
формулам.
Необ одимые и достаточные условия оптимальности также
форм е Куна-Таккера.
а з
твом, что о уму функционала,
претации ое
определится м
ния квадратного уравнения. Рассмотренный метод также
позволяет получить решения по конечным
х
улируются в теорем
Рассмотренные методы близки к методу эллипсоидов,
который имеет полиномиальную степень сложности. Для таких
методов объём вычислений определяется полиномиальной
функцией, зависящей от п раметров m и n адачи оптимизации:
(,) .Pmn mn
α
β
=
84

Симплекс метод имеет экспоненциальную степень сложности,
определяем равенством
(,) exp(,).
ую
P
mn mn
=
Пример. Линейное программирование является основой
решения многих задач экономики, управления и техники. При этом
широкое аспространение имеет одель В. Леон ьева – «затраты-
выпуск», описываемая уравнениями:
р м т
c
1
iijj
i=
,
s
yay
=
+
∑
где - затраты сырья;
ij
a
j
y
- количество затрачиваемого сырья;
i
y
- количество готового продукта. По сути, это модель «вход –
выхо с
Таким образом, рассмотренные численно-аналитические
методы минимизации на компактных множествах позволяют
формировать специальные классы методов и алгоритмов.
ли
фу
е з
путем сведения ограничений задачи к
канон й
д» для тационарного режима объектов управления в
экономике. На множестве моделей данного типа можно
сформулировать комплекс задач линейного программирования для
анализа экономики.
с
2.4. Минимизация нейных и кусочно-линейных
нкционалов с линейными и интервальными ограничениями
Решени адач линейного и кусочно-линейного
программирования с линейными и интервальными ограничениями
можно определить
ическо форме. Пусть рассматривается следующая задача:
вычислить вектор
x
*
=
arg min
ϕ
()
x
=
c
T
x
|
Ax
=
bx
-
≤
x
≤
x
+
,
. (1)
Рассмотрим решение экстремальной задачи минимизации
85
линейного и кусочно-линейного функционалов при ограничениях
типа равенств и двухсторонних неравенств:
,.
A
xb x xx
−
+
=≤≤
(2)
Двухсторонние ограничения в (2) можно преобразовать
эквивалентным образом:
,.xx x x
+
−
≤
−≤−
Последние соотношения иллюстрируют переход от двустороннего
огран
е задач линейного
программирования, на первом этапе можно ввести
ательные свободные неотрицательные переменные и
я
0.
ичения к двум односторонним ограничениям.
Для сведения ограничений к канонической форме,
используемой в канонической форм
1
y
2
y
неотриц
в систему ограничений типа (2). Тогда ограничени задачи можно
представить в виде:
1
,,Ax b x y x
+
=−=
212
,0,xy y y
−
x
−
+=− ≥ ≥
(3)
ств» и «типа
нерав в» ф м й
В результате получаем систему ограничений, в которой
имеется две группы ограничений: «типа неравен
енст . Векторно-матричная ор а ограничени типа
равенств в (3) примет вид:
1
11
00
0.
xb
A
2
0
A
zEE y xb
+
⎛⎞⎛⎞
⎛⎞
⎜⎟⎜⎟
⎜⎟
=− ==
⎜⎟⎜⎟
⎜⎟
EE
yx
−
⎜⎟
⎜⎟⎜⎟
−
⎝⎠
⎝⎠⎝⎠
овательно, после введения вектора новых пере
е
0.
(4)
След менных
12
1
T
z (, , )xyy
можно представить ограничения (3) в вид :
12
11
,0,Az b y y=≥≥
86
Соотношения (4) не являются канонической формой т.к.
имеются отрицательные
,
переменные в виде вектора ,
компоненты которого не имеют ограничения на знак. Поэтому
втором этапе можно воспользоваться методом разно
переменных, в соответствии с которым производится замена
вектора в виде разности неотрицательных векторов:
Тогда (5) с учето
x
на
сти
x
121 2
,0,0.xx x x x=− ≥ ≥
(5)
м замены переменных примет вид:
22
A
z =
0
0
EEE
00AA
E
EE
⎜⎟
−
⎜⎟
⎜⎟
−
⎝⎠
.
2
1
2
⎛
−
⎜⎟
⎞
1
x
x
y
y
⎛⎞
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎝⎠
=
x
x
+
−
⎜⎟
⎜⎟
⎜⎟
−
⎝⎠
где вектор
121 2
2
(, , , )
T
zxx
b
⎞⎛
, (6)
yy
.
В результате ограничения (6) соответствуют канонической
форме. В результате мы сформулировали каноническую форму
исход , поскольку исходн
≥
(7)
Приведенные преобразования являются доказательством
утверждения.
дение 1. Каноническая форма задачи линейного
прогр
огр я.
кусочно-линейного
рограммирования: вычислить вектор
ной задачи ая задача (1)
преобразована к задаче: вычислить вектор
*
212222
arg min{ | , 0},
T
zczAzbz==
где
1
(,cc=−,0,0).
T
c
Утверж
аммирования (1) может быть представлена в виде (7).
Утверждение можно модифицировать для решения задачи
кусочно-линейного пр аммировани
Утверждение 2. Задача
п
87

x
*
=
arg min
ϕ
()
x
=
c
T
||
x
|
Ax
=
b
,
x
-
≤
x
≤
x
+
∈
R
n
преобразуется к задаче линейного программирования в каноничес-
форме:
2
≥
(9)
ных переменных и метод
разно ти о
ммирования к канонической
ме и использовать для их решения симплекс-метод.
ова основная идея формулировки задач линейного
, геометрическая интерпретация и свойства ее решений.
кой смысл имеют локальные условия оптимальнос
сны
3 ущ да б
базисному решению.
(8)
кой
*
2
z=
22222
arg min{ ( ) | , 0},
T
zczAzbz
ϕ
==
где вектор параметров целевой функции имеет вид:
T
2
c= (00).cc
Таким образом, введение свобод
сти переменных позволяют свес граничения задач
линейного и кусочно-линейного програ
фор
Контрольные вопросы
1. Как
программирования
2. Ка ти семейства
бази х решений в задаче линейного программирования.
. В чем с ность перехо от одного азисного решения к другому
4. В чем состоит идея вычисления семейства обратных матриц,
необходимых при решении задач линейного программирования.
5. Какие преимущества и недостатки имеют численно-аналитические
методы минимизации линейных функционалов на компактных множествах.
88
3. МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
ВЫПУКЛЫХ ФУНКЦИОНАЛОВ
Методы безусловной минимизации позволяют определить
минимум выпуклых функционалов при отсутствии ограничений
на переменные, т.е. в условиях, когда допустимая область
ешений совпадает со всем пространством. Эти методы и
огут быть составной частью методов условной оптимизации.
3.1. Метод наискорейшего спуска
Метод наискорейшего спуска является наиболее простым по
ычисли объема
вычисл
1. Вычис м решение
задачи
р
м
в тельной схеме и требует относительно малого
ительной работы.
лительная схема метода. Рассмотри
безусловной минимизации постановке: вычислить вектор
arg min{ ( ) | }
n
x
∗
=ϕ∈xx , (1)
где функционал
()
в
ϕ
x
удовлетворяет условию выпуклости.
()
ϕ
x
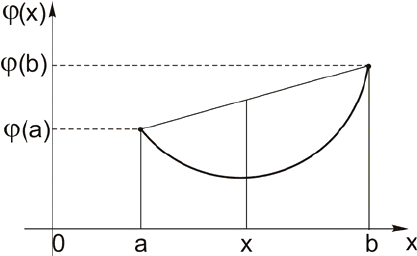
Определение 1. Функционал называется выпуклым
функционалом на интервале
, если выполнено
усло
1
'"
[, ] [,]xx ab=
вие
((1))()(1)(),0
λ
λ
′′
ϕ+−xx
λ λ λ
′′ ′′
≤ϕ+−ϕ ≤≤x x
.
Свойство выпуклости функционала иллюстрируется на рис. 3.1.
Рис. 3.1. Иллюстрация выпуклой функции
89

Необходимо учитывать, что для выпуклых на интервале
ф й
минимум, а в общем (невыпуклом случае) метод приводит к
одному из локальных минимумов. Для вычисления точки
минимума выпуклой функции строится последовательность
ункционалов метод наискорейшего спуска доставляет глобальны
{}
k
x
,
сходящаяся к указанной точке с элементами вида
k1kkk
α
+
=+xx p
,
(1.а)
где и – последующее и предыдущее приближения; -
1k +
x
направление
k
x
д
k
p
вижения из точки
x
;
k k
α
– шаг в направлени .
Выб е
и
p
k
ор направления определя т ряд методов. В данном случае
направление
k
p
определяется как вектор антиградиента
функционала:
()
kkk
Δ
′
′
=−ϕ =−ϕpx
,
где
1
,...,
T
⎛⎞
∂ϕ ∂ϕ
′
ϕ=
⎜⎟
– градиент функциона
k
kn
xx∂∂
⎝⎠
ла. В результате
вычислительная схема метода принимает вид
k
1kk kk
α
+
′
=
−ϕxx
.
(1. )
Алгоритм метода наискорейшего спуска (1.б) содержит
параметр
k
б
α
, которого может быть выполнен различным
образом. Весьм
выбор
а важно, чтобы выбор параметра
k
α
обеспечивал
сходимость оследовательности { } ке минимума.
еорема о сходимости метода наискорейшего спуска
адывает ограничения
п
k
x
к точ
Т
накл на выбор скалярного параметра
k
α
.
). Пусть выполнены условия:
1). Функционал
(
Теорема 1 (о сходимости
ϕ
)x
ограничен снизу;
2). Градиент функционала
′
ϕ
()x
удовлетворяет условию
90
