Козлов В.Н. Системный анализ и принятие решений

Липшица

,;

n

L

′′

ϕ( )−ϕ( ) ≤ − ∀ ∈

xy xyxy

3) раметр

k

Па

α

, выбирается из условия

,), 0 1

kkk

(

ε

αε

′

ϕ( ) − ϕ( ) ≤ ϕ < <xx p

.

(2)

я р н

Тогда дл п едельного з ачений градиента функционала

выполнено необходимое условие оптимальности

0

k

k→∞

′

ϕ

⎯⎯⎯→ .

ий

те оследовательность (1.б), соответствующая методу

наиск уска, сходится к стациона ой точ

функционала

Другими словами, при выполнении указанных услов

оремы п

орейшего сп рн ке

(

ϕ

)x

.

ние функционала,

пользуясь теоремой о среднем:

венства слагаемое

Доказательство. Рассмотрим прираще

() ( ) ( , ), ( ), [0,1]

kkср kkср k

θθ

′

ϕ−ϕ =ϕ − =+ − ∈

xx xxxxxx .

Добавим и вычтем в правой части последнего ра

k

'

(,

k

ϕ

−x

)

k

x

. Тогда п

олучим

() ( ) ( , ) ( , )

kkkkср kk

′

′′

ϕ−ϕ = − +ϕ−ϕ−

x x xx xx,

(2)

где

'

kk

ϕ

α

ϕ

−

=

−x

в сил вычислитель й схемы алгоритма

наискорейшег

k

x

у но

о спуска (1.б).

Дале к и ал

чим цепочку соотношений:

е проведем оцен и приращен я функцион а с учетом

равенства (2). В результате полу

2

222

() ( ) ( , )

(1 ).

kkkkck

kk

kkk

L

LL

k

α

αα

αα α α

′

′′

ϕ−ϕ ≤−ϕϕ+ − ⋅ϕ

′′

≤− ϕ + − ⋅ ϕ =

′′′

=− ϕ + ϕ = ⋅ ϕ − +

xx xx

xx

≤

91

Из последних соотношений следует, что для монотонного

я функционала уменьшени необходимо, чтобы выполнялось

еравенство: н

1 L

α

ε

−+ ≤

.

следует, что скалярный параметр Откуда

α

должен

выбираться из условия

(1 ) / L

α

ε

<−

, и для того, чтобы было

0

α

>

,

метрпара

ε

должен таким, чтобы

01

быть

ε

<

.

Таким образом, при выборе шага из условия

k

α

1

()() (

,

)

kk kk

ε

α

+

′

ϕ−ϕ≤ϕxx

p

.

(3)

Функционал

(

ϕ

)x

монотонно уменьшается, и в силу ограниченно-

сти тот функционал на последовательности { достигает

точки минимума.

Условия сходимости позволяют сформулировать алгоритм

с

Выбираетс произвольный вектор – начальное

приб .

снизу э }

k

x

метода. Алгоритм метода формулируется в соответствии

ограничениями теоремы на выбор шага.

Шаг 1. я

0

лижение Полагается

x

k

=

x x

.

Шаг 2. Выбирается ое значение

0

произвольн

α

.

Шаг . Определяется новое приближение 3

k1kkk

α

+

′

=

−ϕxx

.

Шаг 4. Вычисляется

1

()( )

kkkk

ϕ

ϕα

′

=

+

−ϕxx

и

()

k

ϕ

x

.

Шаг 5. Если

1

()() (,),0

kk kk

ε

αε

+

′

ϕ−ϕ≤ϕ <

xx p

<

, то значение

α

принимает качестве искомого:

k

ся в

α

=

, и происходит переход

к шагу 6, иначе производится деление

α

пополам и ыполняется

переход к шагу 4.

в

Шаг 6. Вычисляется новое приближение

1kkkk

α

+

′

=

−ϕxx

.

Шаг 7. Проверяется условие стационарно ти

с :

2

(,)

′′′

ϕ=ϕϕ≤

111kkk

+++

и если

, 0

δδ

>

,

2

1

,

k

δ

+

′

ϕ≤

, то вы тсполняе я переход к шагу 8, иначе – к

шагу 2, положив

1kk+

=xx

.

92

Шаг 8. Останов.

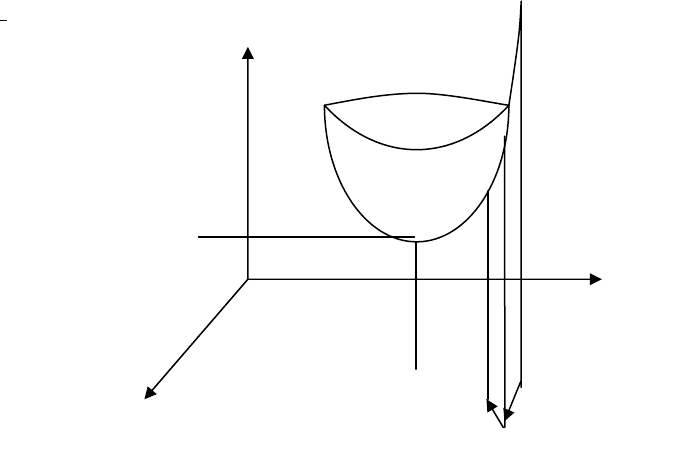
Геометрическая ин есс вытерпретация проц а числений

прив .2.

:

едена на рис. 3

ϕ

()

x

*

x

1

x

*

x

∈

R

0 n

x

2

x

2

x

1

ллюстрация процесса минимизации

ро

Рассмотрим вычислительную схему метода наискорейшего

пуска на примере.

Пример. Пусть ерном пространстве задан

вадратичный

Рис. 3.2. И

функционала в двумерном п странстве

с

в двум

22

12 1 2

() 10 6 39xxx x x

ϕ

=

+− − +

к функционал .

ычислить точку минимума ерном пространстве.

ние ательно шаги алгоритма.

Шаг 1. Задается

−

. Полагается .

Шаг 2. Выбирается

В в двум

трим последовРеше Ра. ссмо

0102

( ) (7, 2)

T

xx==x

0k

=xx

,

0,

0

3

α

=

.

Шаг 3. Определяетс то го приближения:

я век р ново

11 1

xx

22 2

1

26 1,0

kk

xx x

+

210

5, 6

0,3

x

−

⎡⎤ ⎡⎤ ⎡ ⎤

⎡

⎤

==−

⎢⎥ ⎢⎥ ⎢ ⎥

⎢

⎥

−

⎣

⎦

⎣⎦ ⎣⎦ ⎣ ⎦

.

аг 4. Вычисляется значение функционала в новом и

пред

Ш

ыдущем приближениях:

1

()9,64,()34

kk

ϕϕ

+

=

=xx

.

Шаг 5. Проверяется выполнение условия стационарности –

93

нерав паенства ти (2):

1

() ( ),0 1

kk k

() ,

k

ε

αε

+

ϕ−ϕ≤ϕ <<

x p

, торое

выполняется п начении пара

′

x

метров

0,3, 0,1

αε

==

,

ко

ри з а также

условие

'

( , ) ([4, 10],[4, 10]) 116

kk

p

ϕ

=− − =

. Принимается

0,

k

α

= 3

и

выпо шагу 6.

вектор

,0

лняется переход к

Шаг 6. Вычисляется

1

0,3

1101

kkkk

α

+

745,8

⎡

⎤⎡⎤⎡⎤

′

=−ϕ= − =

⎢

⎥⎢⎥⎢

−−

⎥

⎣

⎦⎣⎦⎣

xx

⎦

.

Шаг 7. веряется условие стационарности (2): Про

2

1

,

k+

′

ϕ

переход

выполнение шагов 2 позволяет

опред

0,1

δ

≤=

которое не выполняется, и выполняется к

шагу 2. Последовательное -7

елить значения

k

x

:

2

[5,32

|

2, 20]

T

=x

,

3

[5,12

|

2,68]=x

T

,

4

[5,05

|

2,87]

T

=x

. Реш итерации

5

[5,02

е , ние полученное на пятой

|

2,95]

T

=x

, соответствует приближе с учетом

стациона

Необходимо иметь в виду,

нному р

ограничения нормы градиента функционала в окрестности точки

рности функционала.

что в силу утверждения теоремы 1

сходи еская при бесконечно большом

числе шагов алгоритма.

Рассмотренный метод может использоваться самостоятельно,

а также жить частью более сложных вычислительных

алгор ач условной

минимизации.

Н ляет я методом второго орядка, поскольку

для отыскания т з с

аппроксимация

ешению

мость метода – асимптотич

слу

итмов минимизации, в частности при решении зад

3.2. Метод Ньютона

Метод ьютона яв с п

очек минимума исполь ует я квадратичная

функционала в окрестности очередного

приближения к решению.

На основе этой идеи строится

вычислительная схема метода.

94

1. Вычислительная схема метода. На отдельных этапах

алгоритма метода Ньютона строятся квадратичные аппроксимации

1

() ( ) ( , ) ( ( ), )

2

kk k k k k

ψ

′′′

=ϕ + ϕ − + ϕ − −

x x xx xx xx

,

(1)

т.е. функционал

()xϕ

в окрестности очередного приближения

аппроксимирует квадратичная функция

()x

Ψ

в соответствии с

(1).

Далее вычисляет этой квадратичной

аппроксимации.

Решение этой задачи существенно проще, чем

реше

в

р п

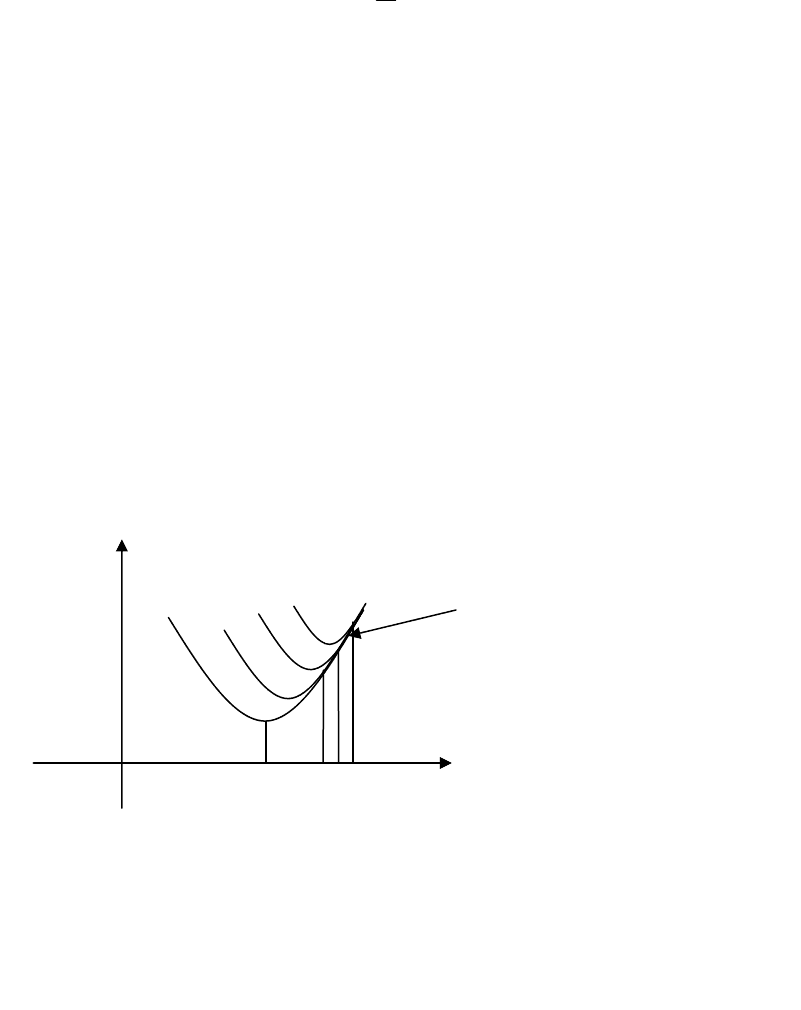
д

метода Ньютона дано на рис. 3.3,

ся точка минимума

ние исходной задачи минимизации. Далее процесс

повторяется до ыполнения сходимости к точке безусловного

минимума. В езультате метод озволяет минимизировать

семейство ква ратичных аппроксимаций исходного функционала.

Наглядное представление идеи

ϕ

()

x

∈

R

1

- квадратичные

аппроксимации

x

∈

R

1

x

*

x

3

x

2

x

1

Рис. 3.3. Геометрическая иллюстрация идеи метода Ньютона

где представ ено семейство квадратичных аппроксимаций л

ϕ

()

x

в

окрестности

x

k

.

В силу строгой выпуклости

()x

ϕ

аппроксимирующие функции

(точнее, семейство новых функций) будут также выпуклыми.

оэтому можно определить единственный минимум

мирующих функций из условия стационарности

П

аппрокси

()/ 0

ψ

∂∂=xx

,

95

используемого для вычисления направлений:

kk

pxx

=

−

:

,

з последнего равенства направление определяется равенством:

k

()O

′′′

ϕ+ϕ⋅ − =xx

kk k n

И

k

p

1

[]

kkk

−

′

′′

=− =−ϕ ϕpxx

,

получить общую схему метода Ньютона в виде

что позволяет

"1'

1

[] .

kkkkk

xx

α

ϕϕ

−

+

=−

(2)

Напомним, что спользуемая адратичная апп ксимация

функционала строится как вторая производная функци

и кв ро

онала по

векторному аргументу, определяемая равенством

2

11

1

( )] ,...,

n

kk

n

nn

⎡

⎤

∂

ϕ

x

22

2

xx

xx x

∂ϕ

⎢

⎥

∂

∂∂

⎢

⎥

⎛⎞

∂ϕ

⎢

⎥

′′ ′ ′

ϕ( )=[ϕ = =

⎜⎟

∂∂

⎢

⎥

⎝⎠

∂

ϕ∂ϕ

⎢

⎥

⎢

⎥

∂∂ ∂

⎣

⎦

xx

…

………

.

Для окончательной формулировки алгоритма метода Ньютона

…

необходимо выбрать шаг

k

α

. Выбор шага неоднозначен.

Рассмотрим метод выбора шага из условия сходимости.

2. Теорема о сходимости метода Ньютона. Для определения

условий, которым должен удовлетворять шаг

k

α

, рассмотрим

вспомогательные сведения. Пусть

()Fx

– произвольная

симметричная матрица, удовлетворяющая условиям

22

((),) , , 0FRR

ρρ

≤≤yxyyy >

(3)

при любых . Тогда, если выбрать вектор

,

n

∈ℜxy

() ()x

′

=

−pFfx

, то

2

((),) ( )

ρ

′′′

ϕ=−ϕ,ϕ≤−ϕxp F

′

, при условии, что

2

0

′

ϕ

() ≠x . Таким

96

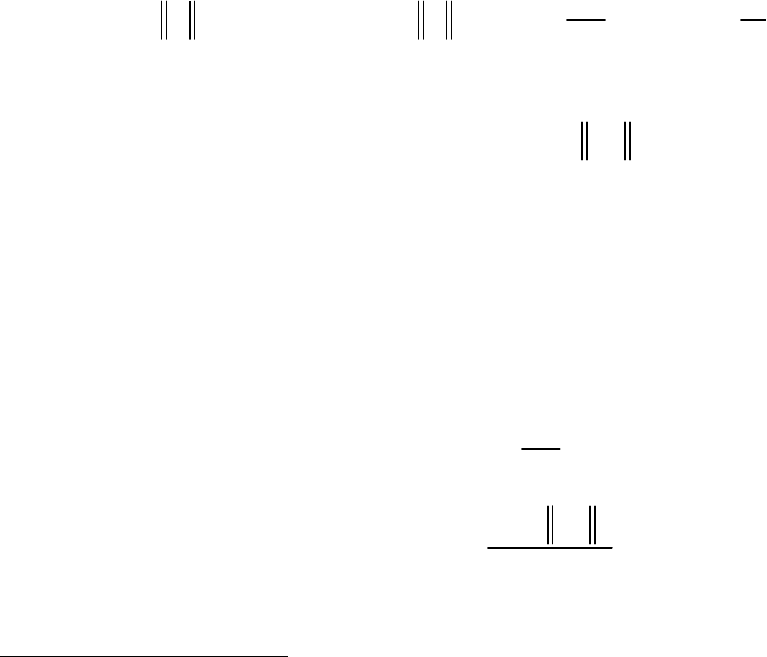
образом, вектор

() ()x

′

=−pFfx

Исходя из этого

определяет направление спуска

функции . , для минимизации можно

сформировать итерационный процесс

.

()ϕ x

3

()ϕ x

1

(), 0, 0,1,..

kkkkkk

k

α

+

=− ϕ > =xx Fx

,

(4)

где

{}

k

F

– последовательность произвольных матриц,

удовл

и йств м

,

отражается на

существе дела, поскольку, если матрица удовлетворяет условию

(3), то для матрицы будут выполнены условия

етворяющая условию (3). Нетрудно видеть, что процедуры (2)

и (4) обладают общим сво ами, приче схема (4) является

более общей.

Для связи процессов (2) и (4) рассмотрим схему

1

,0

kk kk

+

′

=− ϕ

(5)

где используется матрица, обратная к

k

F

. Это не

k k

αα

−

>xx F

k

F

1

k

−

F

22

1

11

2

, 0,m

R

1

(,)mM M

ρ

−

≤≤ =yFyy

,

=>y

и поэтому

1

(,) (, ) 0

kk kkk

m

−

′′′′

1

k

ϕ

=−ϕ ϕ ≤− ϕ <pF .

(6)

В дальнейшем нам понадобится следующая теорема:

Теорема.

Результаты теоремы из раздела 3. охраняют

и для м

1 с

силу етода (5)

.

Доказательство. Если

kk

x

xp

α

=

+

, где

1

kkk

−

′

=

−ϕpF, то:

2

α

ϕ

2

M

α

⎡⎤

() ( ) ( , ) ( , )

(,) 1

2( , )

Kkk kckk

k

kk

α

′′

−ϕ =ϕ + ϕ ≤

′

≤ϕ ++

⎢⎥

′

ϕ

⎢⎥

.

⎣

⎦

xx p pp

p

3

Особенно простое доказательство имеет этот факт в скалярном случае.

97

Но с учетом (3)

2

(,) ( ,)

kk kkk k

′

ϕ=− ≤−pFpp p

.

Следовательно

ρ

() ( ) ( , )1

2

Kkk

M

α

ρ

⎡

⎤

′

ϕ−ϕ =ϕ +

⎢

⎥

⎣

⎦

xx p

.

вытекает, что неравенство (3) будет обязательно

выполняться, если

Отсюда

1/(2)

M

α

ρε

−≥

, т.е.

2(1 )/

M

α

αρε

≤

=−

м . Те

самым обоснован выбор

k

α

.

Поскольку

(,)0

kk

′

ϕ<

p

при 0

k

′

ϕ

≠ , из условия

1

)

kk k

(,

kk

ε

α

′

+

ϕ−ϕ

.

(7)

≤ ϕp

следует, что имеет место условие:

1kk+

ϕ

<ϕ

. Используя (7) и

учитывая ограниченность

()

ϕ

x

лось,

снизу огично тому, как в

теореме 1 п. 3.1 доказыва что

анал

0

k

′

ϕ

→ , уста авливаем,

при . В у оценки (6) это означает, что

н что

(,) 0

kk

k

′

→∞ ϕ →p

сил

0ϕ→. Отсюда в сил

k

′

у й выпуклости сильно

()

ϕ

x

следует схо-

ости решениюдимость последовательн (4) к

x

∗

.

Метод (2) можно рассматривать как пр есс градиентного

, что

оц

11

[]

kk

−−

′

=ϕF

ами,

метода Нью

()x

при выбор

типа (4), считая . Поскольку матрица обладает

требуемыми свойств сходимость метода обеспечивается.

Поэтому процедура тона (2) сходит я к ионарной

очке функционала е шага

k

′′

ϕ

стацс

ϕ

k

α

т из условия ) п.3.1.

ритм метода Ньютона.

то Ньютона. Совокупность шагов

алгор следующи :

аг 1. Выбирается точка . Полагается

(3

Теорема о сходимости доказана, и далее можно

формулировать алго

3. Алгоритм ме да

итма имеет й вид

Ш

0

x

0k

=

xx

.

Шаг 2. Выбирается произвольное число

α

.

98

Шаг 3. Вычисляется вектор

1kk k

α

p

.

+x

+

=

x

Шаг 4. Вычисляется ф и нал

1

()( )

kkk

ункц о

α

+

ϕ

=ϕ +xxp

.

Шаг 5. Если

1

()() )

kk k

(,

k

ε

α

′

+

ϕ−ϕ≤xxϕ

p

, то значение

α

прин исходного

k

имается в качестве

α

=

, и далее - переход к шагу

е производится уменьшение

k

6, инач

α

(путе множения на

множитель

1

:0 1qq

м у

<

) и затем - переход к шагу 4.

k

Шаг 6. Вычисляется очередное приближение:

1

[]

kkkk

α

−

+

′

′′

=

−xx ϕϕ.

Шаг 7. Проверяется условие стационарности

2

111

(,)

kkk

δ

+++

′

ϕ=ϕϕ<

де

0

, г

δ

>

– малое число. Если

2

1k

δ

+

′

ϕ≤

, то

далее к к ш

я в ф

квадратичной функции метод

Ньют а о

й емы метода.

имум квадратичной функции

- переход шагу 8, иначе – агу 2, положив

kk

=xx

Шаг 8. Останов.

1+

.

Дл произвольной (но ыпуклой) ункции имеет место

асимптотическая сходимость. Для

она доставляет минимум з дин шаг.

Перейдем к иллюстрации вычислительно сх

Пример. Вычислить мин

22

12 1 2

51 14 2

x

xxx++− − . ( )ϕ=x

Решение. Для во пользоват

алгоритмом метода Ньютона.

Шаг 1. Выбирается ектор

0

(2, 5,0)

T

=x ;

0k

=xx

.

Шаг 2.

1, 0

минимизации можно с ься

в

Полагаем

0 ,

α

= .

Шаг 3. Вычисляется

1kk k

α

+

=

+xx

p

, где направление

1

21

20 5

[]

02 2 2 4

kkk

x

−

⎡⎤

4

2

⎡

⎤⎡

′′ ′

=−ϕ ϕ = =

⎢⎥

⎤

⎢

⎥⎢⎥

−

⎣

⎦⎣⎦

⎣⎦

(2,0 0) (5,0, 4,0) (7

TT

=+−= сть

решение задачи, доставляющее минимум заданному он

p

.

В результате

T

е

функци алу.

1

, 5, ,0, 1,0)

k

+

x

99

3.3. Метод сопряженных градиентов

сопряженных

Определение 1. Два ктора

Метод сопряженных градиентов позволяет преодолеть

трудности, связанные с обращением матрицы вторых производных

в методе Ньютона.

1. Вычислительная схема метода. Введем понятие

векторов.

ве и

в

p

n

ℜ

k

p

называются

для минимизации квадратичных выпуклых

функ

сопряженными

(А – ортогональными), если (, )0=pAp при

kj

,

T

=AA

.

kj≠

Метод эффективен

ций

1

() ( ,) (,)

2

Cϕ= + +xAxxbx

,

где

A

– симметричная положительно определенная матрица, т.е.

0

,

(,x)>Ax

0

x

≠

.

ации квадратичных функций строитсяДля минимиз

последовательность

{}

k

x

, в которой векторы

k

p

являются

сопряженными:

( , ) 0,1,2,..., 1

kj

kk0,

=

=−pAp ,

Обычно векторы

k

p

строятся следующим образом:

k0

,

01 1kkk

β

++

+

′′

=−ϕ =−ϕ

pp p

,

(1)

причем параметр

1k

β

+

, выбирается из ови сопр нности

k

усл й яже

p

и

1k +

p

. Основная схема алгоритма метода сопряже тов нных град

имеет следующий вид:

иен

1kkkk

α

+

=

+xx

p

,

где параметр

k

α

выбирается из условия

100

Козлов В.Н. Системный анализ и принятие решений

Подождите немного. Документ загружается.