Козлов В.Н. Системный анализ и принятие решений
Подождите немного. Документ загружается.

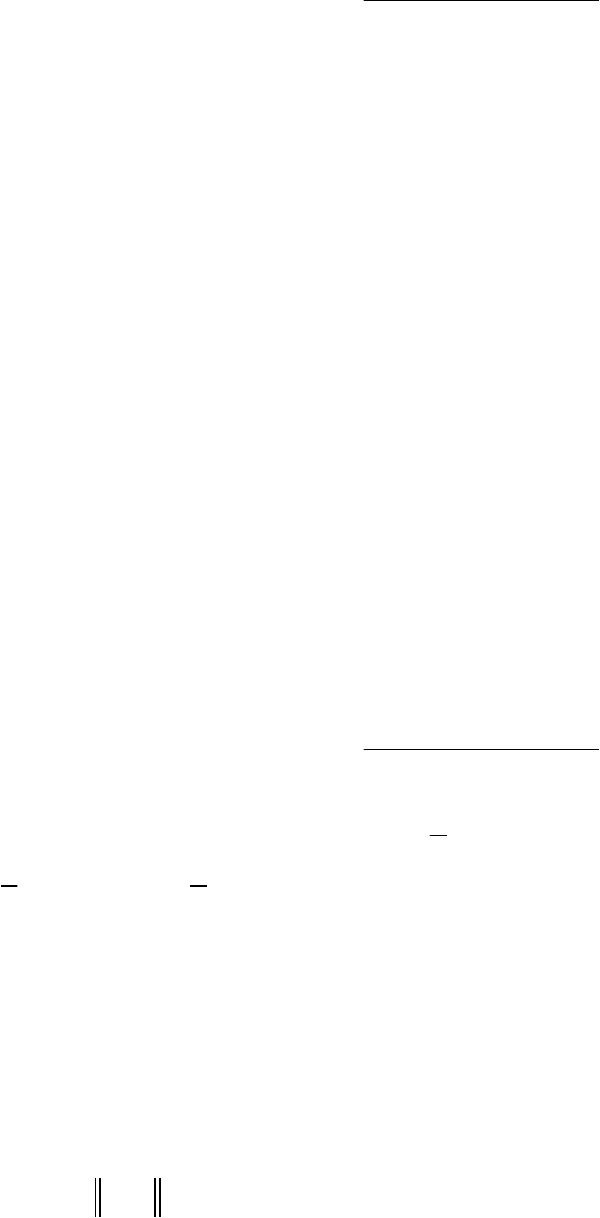
(, ) ( , )
(, )
kk
k
kk
α
k
+
=−
bp x Ap
pAp
.
Р
алгоритм метода опряженных градиентов.
с р О
ставл
бирается произвольная точка
ассмотренные соотношения, позволяют сформулировать
с
2. Алгоритм метода опряженных г адиентов. сновные
шаги алгоритма пред яются следующей последовательностью:
Шаг 1. Вы
0
n
∈
ℜx , полагается
.
Шаг 2. Вычисляется вектор
0
0k =
00
()
k
′
′
=
−ϕ = −ϕpx
, используя
Шаг 3. Если , то переходим к 4, иначе – если
квадратичный , то далее - переход к шагу 8, а и
соотношения (1).
01kn<<−
функционал
ый
шагу
()ϕ x
есл
()ϕ x
– произвольн выпуклый функционал, то - к шагу 7.
Шаг 4. Вычисляется
1kkkk
α
+
=
+xx
p
, где множитель
k
α
определяется из условия
(, ) ( , )
(, )
kk
k
kk
α
k
+
=−
bp x Ap
pAp
,
если – квадратичная;
()ϕ x
kk
a
α
=
, если
()
ϕ
x
произвольная, причем
k
α
такое, что
ar
g
min
{
()
|
0
}
kkk
α
αα
=
ϕ+ ≥xp
.
Шаг 5. Вычисляется направление
()
111kkkk
β
+++
′
=
−ϕ +
p
x
p
, где
1
)
k
111
(, )/(,)(,
kkkkkkk 1
)/(,
kk
β
+++
′
′′′ ′
=−ϕ ϕ −ϕ ϕ = ϕ ϕ
p
−−
′′′
ϕ ϕ
,
Шаг 6. Полагается 1kk
=
+ и далее - переход к шагу 3.
Шаг 7. Так как
()ϕ x
произвольный выпукл нкционал, то ый фу
если
2
1
0
n
δ
−
′′
ϕ≥>
, положим
0
100 1
,(),
nn
k
−−
′
=
=−ϕ =xxp x
и
перех .
ов.
Метод позволяет найти минимум квадратичной положительно
определенной функции за число итераций, не превышающих .
одим к шагу 3, иначе – к шагу 8
Шаг 8. Остан
n
101

Сход ционарной
функ
Н м квадратичной
имость к ста точке произвольной (но выпуклой)
ции асимптотическая.
Проиллюстрируем работу алгоритма на примере.
Пример. айти миниму функции
11
12
22
20
1
⎛
) ( ) ( 4, 6) 18
02
2
xx
xxx
xx
⎛⎞ ⎛⎞
⎞
ϕ( = + − − +
⎜⎟ ⎜⎟
⎜⎟
⎝⎠
⎝⎠ ⎝⎠
.
Решение. Для нахождения минимума можно воспользоваться
ющи
ыбирается , полагаем .
аг 3. Так как , то - переход к шагу 4.
Шаг 4. Вычисляется вектор первого приближения решения
следу м алгоритмом:
0
(4,0 , 8,0)
T
=x 0k =
Шаг 1. В
Шаг 2. Вычисляется направление
)
T
.
00
(4,0, 10,0
′
=ϕ = − −p
Ш
02kn=<=
1000
α
=xx+
p
, где
0 00 00
( , )] / ( , ) 0,5
0
[( , )
α
=− =x Ap p Ap
, так
+bp
)=
как
0
( ,bp) 116=−
,
00
(, 192−xAp
,
00
( , ) 232
=
pAp
.
Тогда
4,0, 8,0)
T
= .
Шаг 5. Вычисляется вектор
1
вектор
T
10
1
,10,0( 0,5( 4,0 ) (2,0, 3,0)
T
−+− =x
1
β
′
=
−ϕ ( ) +
p
x
p
, где параметр
1 0
)0
1100
(, )/(,
′′ ′ ′
ϕ ϕ −ϕ ϕ ϕ
′
=− =
β
так а остальные
векто
ния общих задач математического
прогр рен вариант
мето с методом
сопряженных градиентов. Помимо него известны и широко
применяются другие группы методов безусловной ,
обладающие определенными достоинствами.
нтрольные вопросы
выпуклые фун конечномерных
пространствах.
как
1
(0, 0)
T
′
ϕ=
ры ненулевые.
Таким образом,
1
x
, является решением задачи.
Метод сопряженных градиентов и его обобщения положены в
основу алгоритмов реше
аммирования. В частности, далее будет рассмот
да проектирования градиента, согласованный
минимизации
Ко
1. Как определяются кционалы в
102
2. Как формулируются задачи безусловной и минимизаци в
конеч нствах.
метод
выпуклых функционалов.
4. Поясни е структуру и особенности вычислительных схем методов
наиск , Ньютона и сопряженных градиентов.
т сущность исследования сходимости и выбора шага
метод
6. Какова основная идея и с в сходимости
номерных простра
3. Как формулиру я идея метода наискорейшется основна его спуска,
а Ньютона и метода сопряженных градиентов для минимизации
т
орейшего спуска
5. В чем состои в
е наискорейшего спуска.
с ледо ания и выбора шага в
методе Ньютона.
103

4. МЕТОДЫ УСЛОВНОЙ МИНИМИЗАЦИИ
ВЫПУКЛЫХ ФУНКЦИОНАЛОВ
етоды условной минимизации предназначены для
реше ия задач математического программирования с
ограничениями. Рассмотрены алгоритмы, использующие
необходимые условия оптимальности для задач выпуклой
оптимизации в виде теоремы Куна-Таккера, итеративные
методы проектирования на допустимые области и численно-
аналитические методы.
4.1. Необходимые, достаточные условия оптимальности и
теорема Куна-Таккера
ак уже отмечалось, методы оптимизации можно разделить на
две большие группы: методы прямой минимизации (не
испо ющие необходимые и достаточные условия) и методы,
основанные на необходимых условиях. Применение необходимых
условий экстремума хорошо известно из курса высшей математики
для задач безусловной минимизации. В случае задач на условный
экстремум нами будут даны соответствующие аналоги, в частности,
полученные в теореме Куна-Таккера для задач выпуклого
программирования.
. Общие сведения о задачах выпуклого
программирования. Мы будем устанавливать необходимые и
достаточн
М
н
К
льзу
1
ые условия для следующей задачи: вычислить
ar
g
min
{
()
|}
∗
когда
()ϕ
выпуклый функционал, а опустимые множества
выпуклы, замкнуты и задаются системами равенств и неравенств.
Рассмотрим множество
{ |() }, () ( (),..., ())
T
ff=∈Γ ≥ =xfxbfx x xD ,
(2)
=ϕ∈xxxD
,
(1)
д
где
x
1 m
() , 1, ,
i
f
im=x
– вогнутые непрерывные на множестве
Γ
а
Γ – заданное выпуклскалярные функции, ое и замкнутое
104

n
множество. В частности, Γ может совпадать с пространством
ℜ
.
з теории множест известно что множество (2)
выпукло, поскольку является пересечением выпуклых множеств
И выпуклых в ,
Γ
и
{|
()
}
n
∈ℜ ≥xfxb
. Из непрерывности
()
i
f
x
и замкнутости
множества
Γ следует замкнутость множества D .
Пусть сформулирована задача: вычислить
arg min{ ( ) | }
n
∗
=ϕ∈⊂ℜxxxD ,
(3)
причем
()ϕ x
выпуклый функционал, а удовлетворяет
пров нны ча н ыва
ачей
ярности.
Определение 1.
Если для каждого
D
еде м условиям. Эта зада аз ется
зад выпуклого
программирования.
Множество
D
должно удовлетворять условию регул
(1,)i m= существует
точка
, что влечет за собой
i
i
x ∈ D
()
ii i
f
xb>
,
(4)
D удовлетворяетто множество условию регулярности Слейтера.
Рассмотрим вектор
() ()
=
−hx b f x
,
( )
который характеризует невязки в неравенствах, задающи
5
х
ограничения.
Определение 2.
Функция
(, ) () (, ())
=
ϕ+x
y
x
y
hxL
(6)
(,0)∈Γ ≥x
y
называется функцией Лагранжа
Вект
для задачи
(3).
гранжа. В задачах
выпуклого программирования необходимые и условия
формулируются с помощью седловых точек фу Лагранжа
Определение 3.
Пара
оры
m
∈ℜy
называются множителями Ла
достаточные
нкции .
,
∗
∗
x
y
называется седловой точкой
функции Лагранжа
(, )x
y
L
на множестве
,0y
∈
Γ≥x
, если
105
(,) (, ) (, )
∗∗∗∗
≤
≤x
y
x
y
x
y
LL L
(7)
для всех
,0∈Γ ≥xy
. Последнюю формулу можно записать также
следу
L
еорема 1. Если пара
ющим образом:
00
( , ) min max ( , ) max m
∗∗
∈Γ
==
xx
yy
x y xyLL .
in ( , )
∈Γ
≥≥
xy
Т
,
∗
∗
x
y
– седловая точка функции
Лагранжа
(, )x
y
L
на множестве
,0
∈
Γ≥xy
, то
∗
x
– оптимальная
звернутая форма условий (7) с учетом (6)
имеет вид
)
точка задачи выпуклого программирования.
Доказательство. Ра
()(,()) ()(,()) ()(,()
∗
ϕ+ ≤ϕ+ ≤ϕ+x
∗∗∗∗ ∗
y
hx x
y
hx x
y
hx
.
(8)
венства следует, что
∗
Из левого нера
(,())(,())
∗∗
≤
y
hx
y
hx
,
(9)
поскольку и это неравенство имеет место для любого
значения м
а
0
∗
≥y
0≥
, то
()0
∗
≤hx
. В частности, (9) имеет есто и для
0
y
y
=
, т.е
( )) 0
∗
≥x
, а, следовательно (так как
0
∗
≥y
и
()0
∗
≤hx
),
(,())0
.
(,yh
∗∗
=
yhx
.
(10)
и (
Если ∈x D, то из (1) 5) следует, что
()hx 0
<
, и поэ
будет ь место условие
тому для
∈x D имет
(,())0hx
∗
≤
y
.
(11)
Так как (8) имеет место для всех значений
∈
Γx
(10) и
и в частности, для
, то из правого неравенства (8) и из (11) олучаем
неравенства
∈x D
всех
x
п для
∈D
( ) () ( ,()) ()
∗∗
ϕ≤ϕ+ ≤ϕxx
y
hx x
.
106

∗
∈D
(так как ∈Γx и
0
Но
x ()
∗
hx
≤
) и, следовательно,
∗
x
–
оптимальна а.
Следующая теорема является необход
я точк
имым и достаточным
услов
еорема Куна-Таккера. Теорема формулируется
следующим образом.
Теорема 2.
Пусть в задаче (3) множество
ием оптимальности.
2. Т
{|
()
}
=∈Γ ≥xfxbD
обладает свойством регулярности Слейтера
и достаточным условием оптимальности
ие такого , обы пара
(4).
является существован
Необходимым
чт
,
∗∗
x
y
была
0
∗
≥y
седловой то функции Лагранжа
(, )x
чкой
y
L
на множестве
,0∈Γ ≥xy
Достат аз на теореме 1.
.
очность док а в
Необходимость. Пусть оптимален. Рассмотрим в
)(1n
+
-
∗
x
м
пространстве
1n
+
ℜ
множества
0
0
00 0
()
,(), ,
0
n
∗
⎧⎫
≥ϕ
⎪⎪
==∈ℜ
⎨⎬
≤
⎝⎠
⎪⎪
⎩⎭
zx
PSSxz
z
z
∪
1
,
∈Γ
⎛⎞
∈ℜ
⎜⎟
x
z
z
где определяется для каждого
()Sx
∈
Γx следующим образом
:
0
0
()
()
()
⎧⎫
≥ϕ
⎛⎞
⎪⎪
=
⎨⎬
⎜⎟
≥−
⎝⎠
⎪⎪
⎩⎭
z
zx
Sx
zbfx
z
.
Покажем, что множества и выпуклы. Выпуклость
множества очевидна.
Пусть
P
S
P
0
′
⎛⎞
∈
⎜⎟
z
S
0
′
′
⎛⎞
∈
⎜⎟
z
S
и ,
′
⎝⎠
z
′′
⎝⎠
z
и покажем, что и (,)z
00 0
(,)z z
αα
(1 )(,)
TT T
′′
=
+− ⋅ ∈zzz S для всех
[0,1]
α
∈
. Так как
0
(,)
T
z
′
z∈S
, то найдется такой
∈
Γx , что
107

0
(,) (
′
)
T
′
∈ xzz S
,
и аналогично
0
(,) ()
T
zz x
′′ ′′ ′′
∈S
. Нам остаточно показать, что
0
(,) ()zz Sx∈
, где
(1 )xx x
д
α
α
′′
=+−
выпуклости
(ϕ ()
′
. Из и
)x
f
x
−
следует
(
000
(1 ) ,
zzz
)[ (1)] ()(1)()
[
(1 )()]
[ ( )] (1 )[ ( )]
(1 ) .
() (1 ) ]
[()
b
α
αα α
α
αα
αα
′′′′
ϕ=ϕ +− ≤ϕ +−ϕ
′′
+− =
′′′
=− +− − ≤
′′′
≤+− =
xx x x x
f
fx
bfx bfx
zzz
αα
′′′
≤+− =
αα
α
′′′
−=− +− ≤
′
≤−
bfx b x x
fx
′′
≤
Таким образом, .
Теперь тва щих
точек. Здесь
0
докажем, что множес и
S
не имеют об
(,)zz∈⊂SS
0
P
0
0
()
0
z
zx
∗
⎧⎫
≥ϕ
⎛⎞
⎪⎪
=
⎨⎬
⎜⎟
≤
⎝⎠
⎪⎪
⎩⎭
Для каждог
∈x D
ввиду
P
z
z
.
о оптимальности
∗
x
будет справедливо
0
() ( )z
∗
≥ϕ ≥ϕxx
, но в
00
()z
∗
<
ϕPx
.
Для каждого , такого, что ∈Γx
∉
x D, найдется хотя бы один номер
, но в
такой, что
z≥
0 i
() 0
iii
bf− ≥x
0z
<
P
.
Множества и выпуклы и не имею общих точек. По теореме о
еляющей гиперплоскости существует гиперплоскость,
множества, к
нормали, разделяющей гиперплоск
S
P т
разд
разделяющая эти и существует ненулевой ве тор
ости
0
0
u
⎛⎞
≠
⎜⎟
⎝⎠
u
,
(12)
108
такой, что
,
(13)
для всех
00 0 0
(,) (, )uz uw+≥+uz uw
0
(,)
T
z
∈
zS и
00
(,)
T
w
∈
wP
Поскольку множеству принадлежат точки со сколь угодно
большими по модулю отрицательными компонентами, то
еобходимо должно быть
0
P
н
(
)
0
,0≥u .
(14)
Неравен
T
u
ство (13) остается справедливым и тогда, когда
принадлежит границе поэтому, выб
, по чим для всех
0
(,)
T
w w
()=ϕ
P
w
лу
; рав
00
, (), ( ), 0zw
∗
= − =ϕ =xz bfx x
∈Γx
00
() (, ()) )u(u
∗
ϕ+ − ≥ϕxubfx x
.
(15)
Убедимся, что . Предположим, что . Тогда
Γ
.
как (см. (14)) и
(15)
0
0u >
0
0u =
примет вид
(, ()) 0,−≥∀∈ub f x x
Так
0u > 0u
≠
(см. (13)), а для всех будет
∈x D
справедливо
() 0
−
≤bfx
,
то при
0
i
u >
равенство
() 0
ii
bf
−
=x
,
будет выполняться для всех
∈
x D; что противоречит свойству
ти Слейтера.
, из предположения
регулярнос
Значит
0
0u
=
след т, что , а
ротиворечит (12). Итак, .
ь , тогда (15) примет вид
уе это
0=u
п
0
0u >
1
0
0u
−
∗
=≥yu
Пуст
( ) () ( , ())
∗∗
ϕ≤ϕ+ −xx
y
bfx
.
109
ех ∈Γx , и для
∗
=xx
. следует
(
для вс Отсюда
, ())0
∗
−
≥b fxy
.
(16)
Но , а (так как
0
∗
≥y
()0
∗
−≤bfx
∗
∈
x D
), поэтому.
(, ())0
∗∗
−
=yb fx
.
(17)
значения
0≥y
удет спра в
Для любого б ведли о
(, ( )) 0
∗
−
≤yb f x
.
(18)
Из неравенств (16)-(18) получаем
()(
∗
ϕ+x , ()) ()(, ()) ()(, ())
∗∗∗∗∗
− ≤ϕ+ − ≤ϕ+ −bfx x
y
bfx x
y
bfx
y
для всех или
,0∈Γ ≥xy
(,) , ) (, )
∗∗∗∗
(
≤
≤x
y
x
y
x
y
LL L
что соответствует неравенствам седловой точки.
3. Дифференциальные условия Куна-Таккера. ля
енения весьма важен случай
дифференцируемости ограничений.
Теорема 3.
Если функция
Д
практического прим
()x
ϕ
и
()
f
x
д
задачи выпуклого
программирования
(2) непрерывно ифференцируемы на
множестве
{|
0xxΓ= ≥
, то для го, пара то чтобы
**
,
xy
}
была
седло гвой точкой функции Ла а в области
0, 0
ранж
x
y
,
≥≥
необходимо и достат выполненияочно следующих условий,
приве в табл.
4.1
Таблица
денных
.
4.1
*
*
,0
∂
⎛⎞
=
⎜⎟
*
0
∂
≥
∂x
L
∂
⎝⎠
x
x
L
*
0≥x
*
0
∂
≥
∂y
L
*
*
,0
⎛⎞
∂
=
⎜⎟
∂
⎝⎠
y
y
L
*
0≥y
110
