Козко А.И., Чирский В.Г. Задачи с параметром и другие сложные задачи
Подождите немного. Документ загружается.

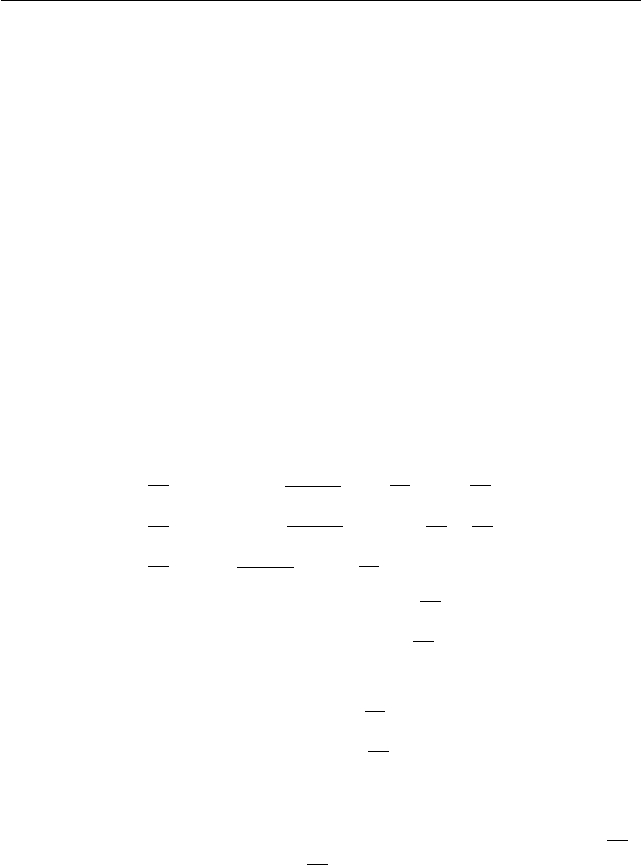
§1.14. Метод областей 101
Остаётся выписать ответ в терминах (y; b): если b ∈ [0; 1/2], то
y ∈ (b; 1 − b); если b ∈ (1/2; 1], то y ∈ (1 − b; b); если b > 1, то y ∈ [0; b).
II. Решим систему (1.9) аналитически. Для этого нам потребуется
сравнить корни y
1
= b, y
2
= 1 − b между собой и с нулём. С нулём
сравниваем, так как нам требуются неотрицательные корни. Из ур ав-
нений
b = 1 − b, b = 0, 1 − b = 0
находим решения b = 0, b = 1/2, b = 1. Значит, по переменной b иссле-
дуем систему (1.9) на каждом из участков по отдельности: b ∈ [0; 1/2],
b ∈ (1/2; 1], b > 1. И опять приходим к ответу в терминах (y; b): если
b ∈ [0; 1/2], то y ∈ (b; 1 −b); если b ∈ (1/2; 1], то y ∈ (1 −b; b); если b > 1,
то y ∈ [0; b).
Вернемся к переменным (a, x):
b ∈ [0; 1/2], y ∈ (b; 1 − b),
b ∈ (1/2; 1], y ∈ (1 − b; b),
b > 1, y ∈ [0; b)
⇐⇒
⇐⇒
√
2a ∈ [0; 1/2],
√
x + 2a ∈ (
√
2a; 1 −
√
2a),
√
2a ∈ (1/2; 1],
√
x + 2a ∈ (1 −
√
2a;
√
2a),
√
2a > 1,
√
x + 2a ∈ [0;
√
2a)
⇐⇒
⇐⇒
a ∈ [0; 1/8], x + 2a ∈ (2a; 1 − 2
√
2a + 2a),
a ∈ (1/8; 1/2], x + 2a ∈ (1 − 2
√
2a + 2a; 2a),
a > 1/2, x + 2a ∈ [0; 2a)
⇐⇒
⇐⇒
a ∈ [0; 1/8], x ∈ (0; 1 − 2
√
2a),
a ∈ (1/8; 1/2], x ∈ (1 − 2
√
2a; 0),
a > 1/2, x ∈ [−2a; 0).
Ответ. При a < 0 решений нет; если a ∈ [0; 1/8], то x ∈ (0; 1−2
√
2a);
если a ∈ (1/8; 1/2], то x ∈ (1 − 2
√
2a; 0); если a > 1/2, то x ∈ [−2a; 0).
Пример 36. Докажите, что множество, заданное на координатной
плоскости условием
|3x + 6| + |2y + 3x − 2| < 6,
102 Часть 1. Основные задачи и методы их решения
является параллелограммом с центром в точке пересечения прямых
3x + 6 = 0, 2y + 3x − 2 = 0, которые являются диагоналями данного
параллелограмма. Найдите площадь параллелограмма.
Решение. Заметим, что
|a| + |b| < c ⇐⇒
(
|a + b| < c,
|a − b| < c.
Действительно, это легко проверить, исследуя знаки чисел a и b. Ис-
пользуя данное замечание, находим, что исходное неравенство равно-
сильно системе
(
|(2y + 3x − 2) + (3x + 6)| < 6,
|(2y + 3x − 2) − (3x + 6)| < 6
⇐⇒
⇐⇒
(
|2y + 6x + 4| < 6,
|2y − 8| < 6
⇐⇒
(
|y + 3x + 2| < 3,
|y − 4| < 3.
7
4
1
y = 1 − 3x
y = −3x − 5
x
y
−4 −2
O
A
B C
D
E
Рис. 1.69. Множество −5 < y + 3x < 1
Решением неравенства
|y + 3x + 2| < 3
является множество −5 < y + 3x < 1, см. рис. 1.69.
Решением неравенства
|y − 4| < 3
§1.14. Метод областей 103
y = 1
y = 7
x
y
−4 −2
O
A
B C
D
E
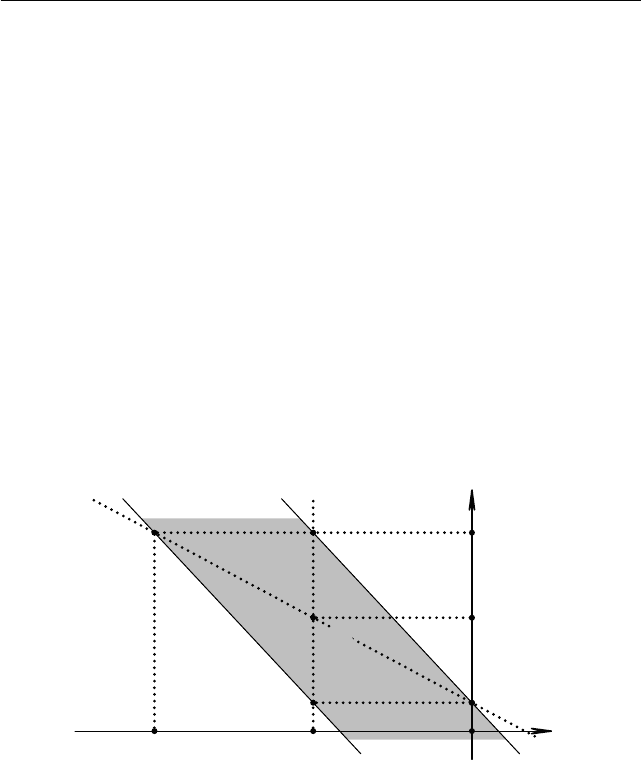
Рис. 1.70. Множество 1 < y < 7
является множество 1 < y < 7, см. рис. 1.70.
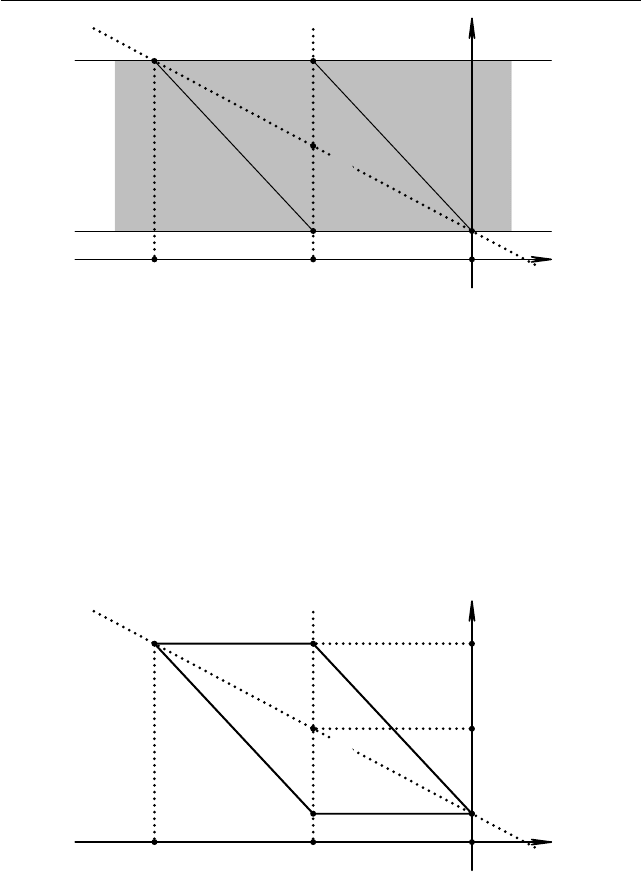
Пересечением данных множеств (−5 < y + 3x < 1 и 1 < y < 7)
действительно является параллелограмм со сторонами
AB : y + 3x + 5 = 0, BC : y = 7,
CD : y + 3x − 1 = 0, DA : y = 1,
7
4
1
y = 1 − 3x
y = −3x − 5
2y + 3x − 6 = 0
3x + 6 = 0
(−2, 4)
x
y
−4 −2
O
A
B C
D
E
Рис. 1.71
Отсюда получаем, что диагоналями данного параллелепипеда дей-
ствительно являются прямые AC : 3x + 6 = 0, BD : 2y + 3x − 2 = 0,
которые пересекаются в точке (−2; 4). Найдём площадь парал лел о-

104 Часть 1. Основные задачи и методы их решения
грамма:
S
ABCD
= AC · AD = 2 · 6 = 12.
Ответ. S
ABCD
= 12.
Задача 200 (филологический факультет (июль), 2001, № 5 (5)).
При каких значениях параметра a на плоскости (x; y) существует круг,
содержащий все точки, удовлетворяющие системе неравенств
2y − x 6 1,
y + 2x 6 2,
y + ax > −1.
Задача 201 (ЕГЭ (демо), 2006, С5). Шесть чисел образуют возрас-
тающую арифметическую прогрессию. Первый, второй и четвертый
члены этой прогрессии являются решениями неравенства
log
0,5x−1
log
4
x − 11
x − 8
> 0,
а остальные не являются р ешен иями этого неравенства. Найдите мно-
жество всех возможных значений первого члена таких прогрессий.
Задача 202 (высший колледж наук о материалах (апрель), 2000,
№ 2). Найдите площадь фигуры, координаты точек которой удовле-
творяют соотношениям
x
2
+ y
2
6 9,
y + 1 > 0,
3y + 6 > 2|x|.
Задача 203 (факультет почвоведения (май), 1996, № 6). Опреде-
лите площадь фигуры, распол оженной на координатной плоскости и
состоящей из точек (x; y), удовлетворяющих неравенству
log
(x
2
+y
2
)/2
(x − y) > 1.
Задача 204 (географический факультет (июль), 2005, № 4 (6)).
Найдите периметр фигуры, точки которой на координатной плоскости
(x; y) удовлетворяют системе
(
y >
|x − 2| − 1
,
x
2
+ y
2
< 4x + 2y − 3.

§1.14. Метод областей 105
Задача 205 (ИСАА, 1997, № 5 (7)). Найдите площадь фигуры,
заданной на координатной плоскости условиями
(
y 6
√
4 − x
2
,
y > |x − 1| − 3.
Задача 206 (факультет почвоведения (май), 2002, № 6 (7)). Опре-
делите площадь фигуры, расположенной на координатной плоскости
и состоящей из точек (x; y), удовлетворяющих неравенству
x
2
+ y
2
6 6|x| − 6|y|.
Задача 207 (геологический факультет, 2005, № 7 (8)). Найдите все
значения, которые может принимать сумм а x + a при условии
|2x + 4 − 2a| + |x − 2 + a| 6 3.
Задача 208 (экономический факультет (отделение полити чес кой
экономии), 1988, № 4 (6)). Найдите площадь фигуры, заданной на
координатной плоскости соотношением
|y − x
2
/2| + |y + x
2
/2| 6 2 + x.
Задача 209 (экономический факультет (отделение вечернее и ме-
неджмента), 1996, № 6). При каких значениях параметра p площадь
фигуры, заданной на координатной п лоскости уравнением
|2x + y| + |x − y + 3| 6 p,
будет равна 24?
Задача 210 (ИСАА, 2002, № 7). Найдите все значения парамет-
ра a, при каждом из которых система
(
x
2
+ y
2
− 6|x| − 6|y| + 17 6 0,
x
2
+ y
2
− 2y = a
2
− 1
имеет хотя бы одно решение.
Задача 211 (экономический факультет, 1994, № 4). Составьте
уравнение окружности наименьшего радиуса, внутри которой поме-
щается множество, заданное на коорд ин атной плоскости условием
|y − 2x − 1| + |2x − 4| < 4.

106 Часть 1. Основные задачи и методы их решения
Задача 212 (химический факультет (весна), 2000, № 6). При каж-
дом значении параметра b решите неравенство
p
x + 4b
2
> x + 2|b|.
Задача 213 (химический факультет (весна), 1999, № 6). Для каж-
дого значения параметра a, принадлежащего отрезку [−1, 0], решите
неравенство
log
x+a
x
2
− (a + 1)x + a
> 1.
Ответы. 200. a ∈ (−1/2; 2). 201. a
1
∈ (2; 2,5). Указание. Напишите
неравенства для a
1
и d и решите их методом областей. 202. 9(π + 1)/2.
203. S = π/3+ 2
√
3. 204. P = 3π/
√
2+ 2
√
2. 205. S = 2π + 7. 206. 10π +16.
207. [−1; 5]. 208. S = 15/2. 209. p = 6. 210. a ∈ [−6; 1 −
√
13] ∪ [
√
13 − 1; 6]
211. (x − 2)
2
+ (y − 5)
2
= 20. 212. Если |b| ∈ [0; 1/4], то x ∈ (0; 1 − 4|b|);
если |b| ∈ (1/4; 1/2], то x ∈ (1 − 4|b|; 0); если |b| > 1/2, то x ∈ [−4b
2
; 0).
213. Если a = −1, то x ∈ (2; +∞); если a ∈ (−1; −1/2), то x ∈ (1; a + 2] ∪
∪ (1 − a; +∞); если a = −1/2, то x ∈ (1; 3/2) ∪ (3/2; +∞); если a ∈ (−1/2; 0),
то x ∈ (1; 1 − a) ∪ [a + 2; +∞); если a = 0, то x ∈ [2; +∞).
§1.15. Задачи на целые числа
При решении задач в целых числах важную роль играет понятие
делимости чисел. Напомним, что целое число b делит целое чи сл о a,
если существует такое целое число c, что a = bc. Если целое число
делится на 2, то оно называется чётным. Чётными являются числа
0, ±2, ±4, ±6, . . . Общая формула чётного числа: 2n, n ∈ Z. Если
целое число не делится на 2, то оно называется нечётным. Нечётными
являются числа ±1, ±3, ±5, ±7, . . . Общая формула нечётного числа:
2n + 1, n ∈ Z.
Часто бывает полезно знать признаки делимости на 2, 3, 5, 9, 10.
Число делится на 2, если в его десятичной записи последняя цифра
чётная.
Число делится на 5, если в его десятичной записи последняя цифра
равна либо 5, либо 0.
Число делится на 10, если в его десятичной записи последняя циф-
ра 0. Вообще, число делится на 10
n
, есл и n его последних цифр рав-
ны 0.
Число делится на 3, если сумм а его цифр делится на 3.
Число делится на 9, если сумм а его цифр делится на 9.

§1.15. Задачи на целые числа 107
Если произведение целых чисел x, y равно заданному числу k, то
каждое из чисел является делителе м k. Например, уравнение xy = 21
допускает следующие восемь решений в целых числах: (x; y) = (1; 21),
(21; 1), (3; 7), (7; 3), (−1; −21), (−21; −1), (−3; −7), (−7; −3).
Пример 37. Найдите пары целых чисел x и y, удовле творяющие
уравнению 3x
2
− 7y
2
− 20xy = 15.
Решение. Представим исходное уравне ние в следующе м виде:
(3x + y)(x − 7y) = 15.
Поскольку мы решаем задачу в целых числах, 3x + y, x − 7y тоже
целые числа. Число 15 можно представить в виде произведения двух
целых чисел так: 1 ·15, (−1) ·(−15), 15 ·1, (−15) ·(−1), 5 ·3, (−5) ·(−3),
3·5, (−3)·(−5). Поэтому исходное уравнение равносильно совокупности
восьми систем в целых числах.
1.
(
3x + y = 1,
x − 7y = 15.
Умножим второе уравнение на −3 и сложим с первым. Получаем 22y =
= −44, откуда находим y = −2. Теперь из первого уравнения находим
x = 1. Аналогично решим все оставшиеся семь с исте м.
2.
(
3x + y = −1,
x − 7y = −15
⇐⇒ y = 2, x = −1.
3.
(
3x + y = 15,
x − 7y = 1
решений в целых числах нет.
4.
(
3x + y = −15,
x − 7y = −1
решений в целых числах нет.
5.
(
3x + y = 5,
x − 7y = 3
решений в целых числах нет.
6.
(
3x + y = −5,
x − 7y = −3
решений в целых числах нет.
7.
(
3x + y = 3,
x − 7y = 5
решений в целых числах нет.
8.
(
3x + y = −3,
x − 7y = −5
решений в целых числах нет.
Ответ. x = 1, y = 2, x = −1, y = −2.
108 Часть 1. Основные задачи и методы их решения
Пример 38 (ЕГЭ, 2003, № С4). Из области определени я функции
y = log
0,8
a
a
− a
8x+5
x+5
взяли все натуральные числа и сложили их. Найдите все натуральные
значения a, при которых такая сумма будет больше 8, но меньше 15.
Решение. Выпишем ОДЗ данного уравнения:
(
a > 0,
a
a
− a
8x+5
x+5
> 0.
Из последнего неравенства заключаем, что a 6= 1. Для решения этого
неравенства рассмотрим два случая: a ∈ (0; 1) и a ∈ (1; +∞).
I. Пусть a ∈ (0; 1). Тогда
a
a
> a
8x+5
x+5
⇐⇒ a <
8x + 5
x + 5
⇐⇒
(8 − a)x + 5 − 5a
x + 5
> 0 ⇐⇒
⇐⇒ (8 − a) ·
x +
5a−5
a−8
x + 5
> 0.
Решим последнее неравенство методом интервалов. Корень знамена-
теля x
1
= −5, а числителя x
2
= −
5a−5
a−8
. Поскольку при a ∈ (0; 1) спра-
ведливо неравенс тво
5a−5
a−8
= 5+
35
a−8
< 5, мы получаем x
1
< x
2
. Следо-
вательно, решение неравенства при a ∈ (0; 1) имеет вид x ∈ (−∞; x
1
) ∪
∪ (x
2
; +∞). Поскольку в этом случае среди реше ний содержится бес-
конечное множество положительных чисел, условие задачи не выпол-
нено.
II. Пусть a ∈ (1; +∞). Тогда
a
a
> a
8x+5
x+5
⇐⇒ a >
8x + 5
x + 5
⇐⇒
(8 − a)x + 5 − 5a
x + 5
< 0 ⇐⇒
⇐⇒ (8 − a) ·
x +
5a−5
a−8
x + 5
< 0.
Для дальнейшего исследования придётся рассмотреть три случая, в
зависимости от величины числа 8 − a.
IIa. Пусть a ∈ (1; 8). Тогда исходное неравенство равносильно нера-
венству
x +
5a−5
a−8
x + 5
< 0.

§1.15. Задачи на целые числа 109
Поскольку при a ∈ (1; 8) справедливо неравенство
5a − 5
a − 8
= 5 +
35
a − 8
< 5,
как и ранее, мы получаем x
1
< x
2
. Следовательно, метод интервалов
даёт решение x ∈ (x
1
; x
2
) =
−5; −5 +
35
8−a
. При a ∈ (1; 8) выполнено
неравенство −5 +
35
8−a
> −5 +
35
8−1
= 0, откуда вытекает, что x = −4,
−3, −2, −1, 0 будут целыми решениями при любом a из рассм атривае-
мого промежутка. Найдём те a, при которых сумма всех натуральных
решений неравенства будет больше 8, но при этом меньше 15. Из со-
отношений
1 + 2 + 3 = 6 < 8, 1 + 2 + 3 + 4 = 10 > 8, 1 + 2 + 3 + 4 + 5 = 15.
вытекает, ч то x
2
∈ (4; 5]. Отсюда получаем
4 < −5 +
35
8 − a
6 5 ⇐⇒ 9 <
35
8 − a
6 10 ⇐⇒
⇐⇒
35
10
6 8 − a <
35
9
⇐⇒
⇐⇒ −
9
2
6 −a <
37
9
⇐⇒
37
9
< a 6
9
2
.
Данные значения параметра a удовлетворяют условию задачи.
IIб. Пусть a = 8. Тогда решений нет, так как получается неверное
неравенство 0 > 0.
IIв. Пусть a ∈ (8; +∞). Тогда исходное неравенство равносильно
неравенству
x +
5a−5
a−8
x + 5
> 0.
Поскольку при a ∈ (8; +∞) справедливо неравенство
5a − 5
a − 8
= 5 +
35
a − 8
> 5,
мы получаем x
1
> x
2
. Метод интервалов даёт решение x ∈ (−∞; x
2
) ∪
∪ (x
1
; +∞). И в этом случае среди решений натуральных чисел x
бесконечно много, следовательно, условие задачи не выполнено.
Ответ. a ∈ (37/9; 9/2].
110 Часть 1. Основные задачи и методы их решения
Пример 39 (химический факультет (июл ь), 2005, № 5 (6)). Найдите
все пары целых чисел (x; y), удовлетворяющих уравнению
p
2x − y − 3 +
p
2y − x + 3 = 2
p
3 − x − y.
Решение. Найдём ОДЗ данного уравнения:
2x −y −3 > 0,
2y −x + 3 > 0,
3 −x −y > 0
⇐⇒
y 6 2x −3,
y >
x −3
2
,
y 6 x −3
⇐⇒
x −3
2
6 y 6 2x −3,
x −3
2
6 y 6 x −3.
(1.10)
Из последней системы как следствие получаем
x − 3
2
6 2x − 3,
x − 3
2
6 x − 3
⇐⇒
(
3x 6 9,
3 6 3x
⇐⇒ 1 6 x 6 3.
I. Пусть x = 1. Тогда из системы (1.10) следует
(
−1 6 y 6 2,
−1 6 y 6 −1
⇐⇒ y = −1.
Подстановкой в исходное уравнение убеждаемся, что (x; y) = (1; −1)
не является решением:
√
2 + 1 − 3 +
√
−2 − 1 + 3 = 0 6= 2
√
3 − 1 + 1.
II. Пусть x = 2. Тогда из системы (1.10) следует, что
(
−1/2 6 y 6 1,
−1/2 6 y 6 1
⇐⇒ y = 0; 1.
Подставим в исходное уравнение (x; y) = (2; 0):
√
4 − 0 − 3 +
√
0 − 2 + 3 = 2
√
3 − 2 − 0.
Таким образом, (x; y) = (2; 0) является решением исходного уравнения.
Подстановкой в исходное уравнени е убеждаемся, что другая пара
(x; y) = (2; 1) не является решением:
√
4 − 1 − 3 +
√
2 − 2 + 3 =
√
3 6= 0 = 2
√
3 − 2 − 1.
