Коврижных А.Ю., Конончук Е.А. и др. Прикладное программное обеспечение для решения экономических задач

Подождите немного. Документ загружается.

1. Табличный курсор установите в левый верхний угол результирующей

матрицы, например в А7. Введите формулу для вычисления первого

элемента результирующей матрицы =А1 + А4.

2. Скопируйте введенную формулу в остальные ячейки результирующей

матрицы: установите табличный курсор в ячейку А7; наведите указатель

мыши на точку в правом нижнем углу ячейки, так чтобы указатель

мыши принял вид тонкого крестика; при нажатой левой кнопке мыши

протяните указатель до ячейки С7; затем так же протяните указатель

мыши до ячейки С8.

Рис.3.9

3. В результате в ячейках А7:С8 появится матрица, равная сумме исходных

матриц.

Рис.3.9

Подобным же образом вычисляется разность матриц (2.1), только в формуле

для вычисления первого элемента вместо знака + ставится знак –.

Умножение матриц.

Для нахождения произведения двух матриц в Excel используется функция

МУМНОЖ (матрицы хранятся в массивах).

Функция имеет вид МУМНОЖ (массив1;массив2). Здесь массив1 и массив2

— это перемножаемые массивы. При этом количество столбцов аргумента

массив1 должно быть таким же, как количество строк аргумента массив2, и

оба массива должны содержать только числа. Результатом является массив с

таким же числом строк, как массив1 и с таким же числом столбцов, как

массив2.

Массив С, который является произведением двух массивов А и В,

определяется следующим образом: c

i,j

∑

kjik

ba где i — номер строки, а j —

номер столбца.

Рассмотрим примеры умножения матриц.

Пример 3.5. Пусть матрица А введена в диапазон A1:D3, а матрица В — в

диапазон А4:В7. Необходимо найти произведение этих матриц С.

Решение.

1) Выделим блок ячеек под результирующую матрицу. Для этого требуется

найти размер матрицы-произведения. Ее размерность будет, в данном

примере, 3х2. Например, выделим блок ячеек F1:G3.

2) Нажмем на панели инструментов Стандартная кнопку Вставка

функции.

3) В появившемся диалоговом окне Мастер функций в поле Категория

выберите Математические, а в поле Функция — имя функции

МУМНОЖ. После этого щелкните на кнопке ОК.

Рис.3.10

Введем диапазон исходной матрицы А — A1:.D3 в рабочее поле Массив1, а

диапазон матрицы В — А4:В7 в рабочее поле Массив2 (рис.3.10). После этого

нажмем сочетание клавиш CTRL+SHIFT+ENTER.

Рис.3.11

В результате в диапазоне F1:G3 появится произведение матриц:

Пример 3.6

Предприятие выпускает продукцию трех видов: Р1, Р2, РЗ и использует

сырье двух типов S1 и S2. Нормы расхода сырья характеризуются матрицей

⎟

⎠

⎞

⎜

⎝

⎛

где каждый элемент показывает, сколько единиц сырья каждого типа

расходуется на производство единицы продукции. Стоимость единицы

каждого типа сырья задана матрицей-столбцом

⎟

⎠

⎞

⎜

⎝

⎛

С .

Определить стоимость затрат сырья на единицу продукции.

Решение. Каждая строка матрицы соответствует определенному виду

продукции, а столбец – виду сырья. Таким образом, чтобы решить задачу

необходимо перемножить А и С, результат – ветор-столбец из трех элементов,

каждый из которых и определяет стоимость затрат сырья на единицу каждого

вида продукции.

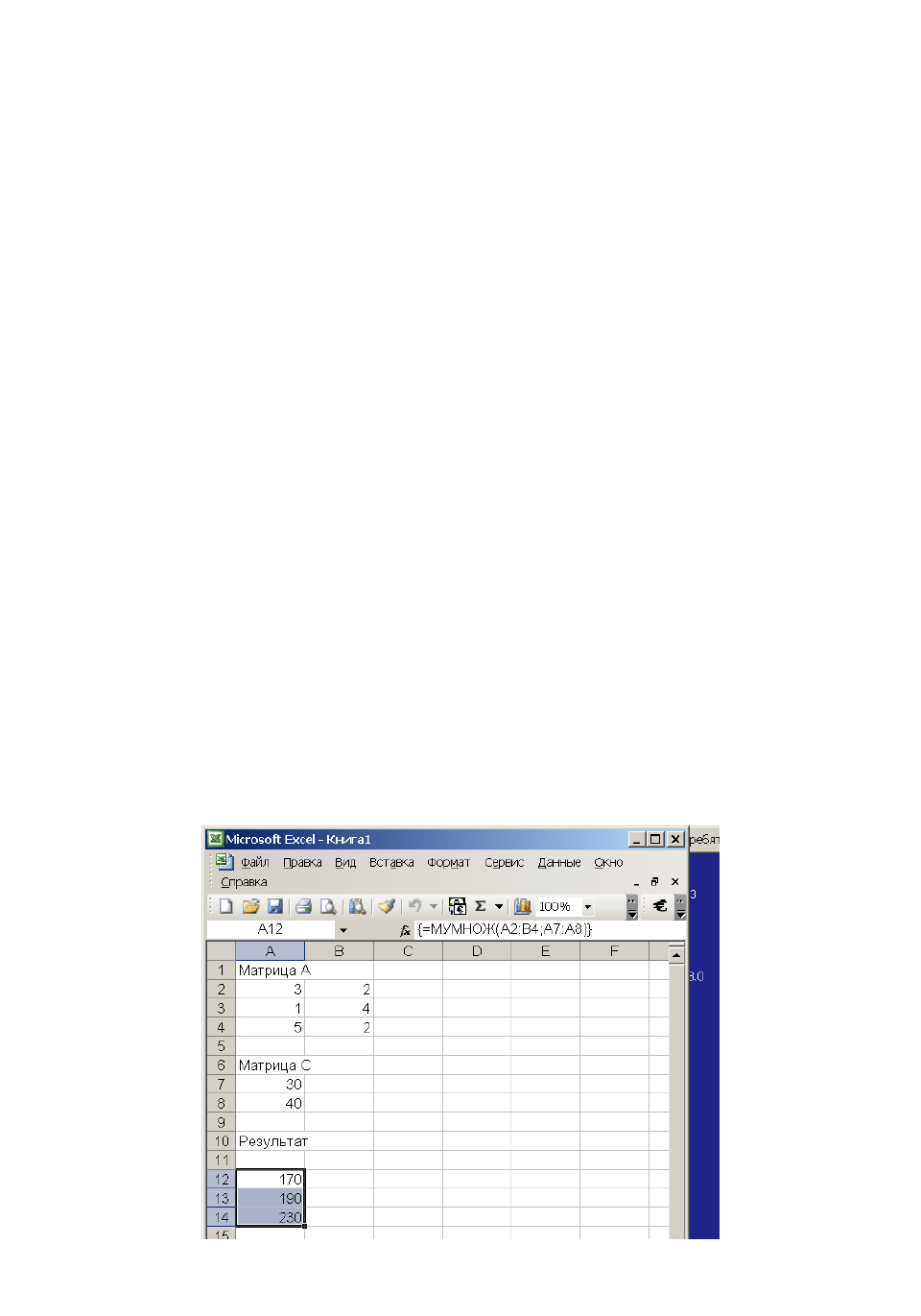
1. Зададим элементы А в диапазоне А2:В4, А элементы С в диапазоне

А7:А8.

2. Для результата выделим диапазон А12:А14.

3. Вставим функцию МУМНОЖ, указав диапазоны исходных данных.

В результате имеем (рис.3.12):

стоимость затрат сырья на единицу продукции Р1 равна 170;

стоимость затрат сырья на единицу продукции Р2 равна 190;

стоимость затрат сырья на единицу продукции Р3 равна 230.

Рис.3.12

Решение систем линейных уравнений

Многие прикладные задачи в технике, экономике и других областям

сводятся к решению систем линейных уравнений, поэтому особенно важно

уметь их решать.

Пусть дана линейная система n уравнений с n неизвестными, где a

ij(

„(i =

1,2....,n ;j = 1.2.....п) – коэффициенты при переменных и b

- свободные члены

уравнений.

⎪

⎩

⎪

⎨

⎧

=+++

bnxaxaxa

bxaxaxa

nnnnn

...

.............................................

...

2211

22222121

11212111

(3.1)

Решением системы (1) называется такая совокупность п чисел (x

, x

,. . . ,x

при подстановке которых каждое уравнение системы обращается в верное

равенство.

Две системы уравнений являются равносильными или эквивалентными,

если они имеют одно и то же множество решений. Система, равносильная

данной может быть получена с помощью элементарных преобразований

системы (1). Систему (1) можно также записать в виде матричного уравнения:

А·х=b (3.2)

где А - матрица коэффициентов при переменных, или матрица системы;

x — вектор – столбец неизвестных:

b — вектор – столбец свободных членов:

Предполагая использование MS Excel для проведения вычислений,

рассмотрим решение системы (1) в общем виде (метод обратной матрицы),

Будем считать, что квадратная матрица системы (А) является невырожденной,

то есть ее определитель отличен от 0. В этом случае существует обратная

матрица А

-1

. Умножая слева обе части матричного равенства (3.2) на обратную

матрицу А

-1

, получим:

-1

·А·х = А

-1

· b, Е·х = А

-1

· b т.к. Е·х = х,

решением системы (3.2) методом обратной матрицы будет столбец:

х = А

-1

b (3.3)

Таким образом, для нахождения вектора х необходимо найти обратную

матрицу коэффициентов и умножить се справа на вектор свободных членов.

Выполнение этих операций в пакете Excel рассмотрено ранее.

Пример 3.7. Пусть необходимо решить систему

⎩

⎨

⎧

=−

4054

723

(3.4)

Решение:

1) Введем матрицу А (в данном случае размера 2 × 2) в диапазон А1:В2

2) Вектор b введем в диапазон С1:С2.

3) Найдем обратную матрицу А

-1

. Для этого:

9 Выделим блок ячеек под обратную матрицу. Например, блок АЗ:В4.

9 нажмем на панели инструментов Стандартная кнопку Вставка

функции;

9 в появившемся диалоговом окне Мастер функций в рабочем поле

Категория выберем Математические. а и рабочем поле Функция —

имя функции МОБР.

9 введем диапазон исходной матрицы А1:В2 в рабочее поле Массив.

9 Нажмем сочетание клавиш CTRL+SHIFT+ENTER;

если обратная матрица не появилась в диапазоне А3:84, то следует

щелкнуть указателем мыши в Строке формул и повторить нажатие

CTRL+SHIFT+ENTER.

Рис.3.13.

В результате в диапазоне А3:В4 появится обратная матрица (рис3.13):

⎟

⎠

⎞

⎜

⎝

⎛

−

0,13043-0,173913

086957,00,217391

4) Умножением обратной матрицы А

-1

на вектор b найдем вектор x.

Для этого:

9 выделим блок ячеек под результат (вектор x).. Например, СЗ:С4 ;

9 нажмем на панели инструментов Стандартная кнопку Вставка

функции;

9 в появившемся диалоговом окне Мастер функций в рабочем поле

Категория выберите Математические, .а в рабочем поле Функция имя

функции — МУМНОЖ. Щелкните на кнопке 0К;

9 в появившемся диалоговое окно МУМНОЖ введем диапазон обратной

матрицы А

-1

в рабочее поле Массив1, .а диапазон столбца b (С1:С2) — в

рабочее поле Массив2. После этого нажмем сочетание клавиш

CTRL+SHIFT+ENTER;

9 если вектор x не появился в диапазоне СЗ:С4, то следует щелкнуть

указателем мыши в строке формул и повторить нажатие

CTRL+SHIFT+ENTER.

Рис.3.14

В результате в диапазоне С3:С4 появится вектор x (рис.3.14). Причем х

= 5

будет находиться в ячейке СЗ, а y = 4. в ячейке С4. Можно осуществить

проверку найденного решения. Для этого найденный вектор x необходимо

подставить в матричное уравнение А·х=b .

Проверка производится следующим образом:•

1) Выделим блок ячеек под вектор b . Например, блок ячеек D1:D2;

2) Нажмем на панели инструментов Стандартная кнопку Вставка функции.

3) В появившемся диалоговом окне Мастер функций в рабочем поле

Категория выберем Математические, а в рабочем поле Функция — имя

функции МУМНОЖ.;ОК.

4) В появившееся диалоговое окно МУМНОЖ введем диапазон исходной

матрицы А в рабочее поле Macсив1, а диапазон вектора x в рабочее поле

Массив2. После этого нажмем сочетание клавиш CTRL+SHIFT+ENTER.

В результате в диапазоне D1:D2 появится вектор b, и, если система решена

правильно, появившийся вектор будет равен исходному (7, 40).

Рис.3.15

Рис.3.16

Пример 3.8. Ресторан специализируется на выпуске трех видов фирменных

блюд: В1, В2, ВЗ. При этом используются ингредиенты грех типов S1, S2, S3.

Нормы расхода каждого из них на одно блюдо и объем расхода ингредиентов

на 1 день заданы таблицей:

Нормы расхода ингредиентов

на одно блюдо (у. е.)

Ингредиент

B1 B2 B3

Расход

ингредиентов

на 1 день(у. е.)

S1 5 3 4 2700

S2 2 1 1 800

S3 3 2 2 1600

Нужно найти ежедневный объем выпуска фирменных блюд каждого вида.

Решение.

Пусть ежедневно ресторан выпускает x

блюд вида B1, x

блюд вида В2 и x

блюд вида ВЗ. Тогда в соответствии с расходом ингредиентов каждого типа

имеем систему:

⎪

⎩

⎪

⎨

⎧

=++

1600223

800112

2700435

321

xxx

Решаем систему аналогично решению предыдущего примера.

1) Введем матрицу системы в А1:С3;

2) Находим матрицу, обратную матрице системы в диапазоне A4:C6;

3) Умножим ее на столбец свободных членов;.

Процесс решения отображен на рисунке 3.17

Рис.3.17

Получен ответ : (0, 500, 300)

Система m линейных уравнений с n неизвестными.

Система m линейных уравнений с n неизвестными имеет вид:

⎪

⎩

⎪

⎨

⎧

=+++

mnmnmm

bxaxaxa

...

.............................................

...

2211

22222121

11212111

(3.5)

Как и система (3.1), система (3.5) может быть представлена в матричном виде

А·х=b

Возможны следующие три случая: m<n, m = n и m>n. Случай, когда m = n.

рассмотрен ранее. В случае если m > n обычно применяют метод наименьших

квадратов. Для этого обе части матричного уравнения системы (3.5) умножаем

слева на транспонированную матрицу системы A

·А·х = А

· b ;

Затем обе части уравнения умножаем слева на матрицу (А

·А)

-1

. Если эта

матрица существует, то система определена. С учетом того, что

(А

·А) (А

·А)

-1

= E, получаем

x = (А

·А)

-1

· b (3.6)

Матричное уравнение (3.6) определяет приближенное решение системы m

линейных уравнений с n неизвестными при m > n.

Пример 3.9 . Пусть необходимо решить систему

⎪

⎩

⎪

⎨

⎧

=−

333

4054

723

Решение.

1) Введем матрицу А в диапазон А1:ВЗ

2) Вектор b = (7, 40, 3) введем в диапазон C1:C3

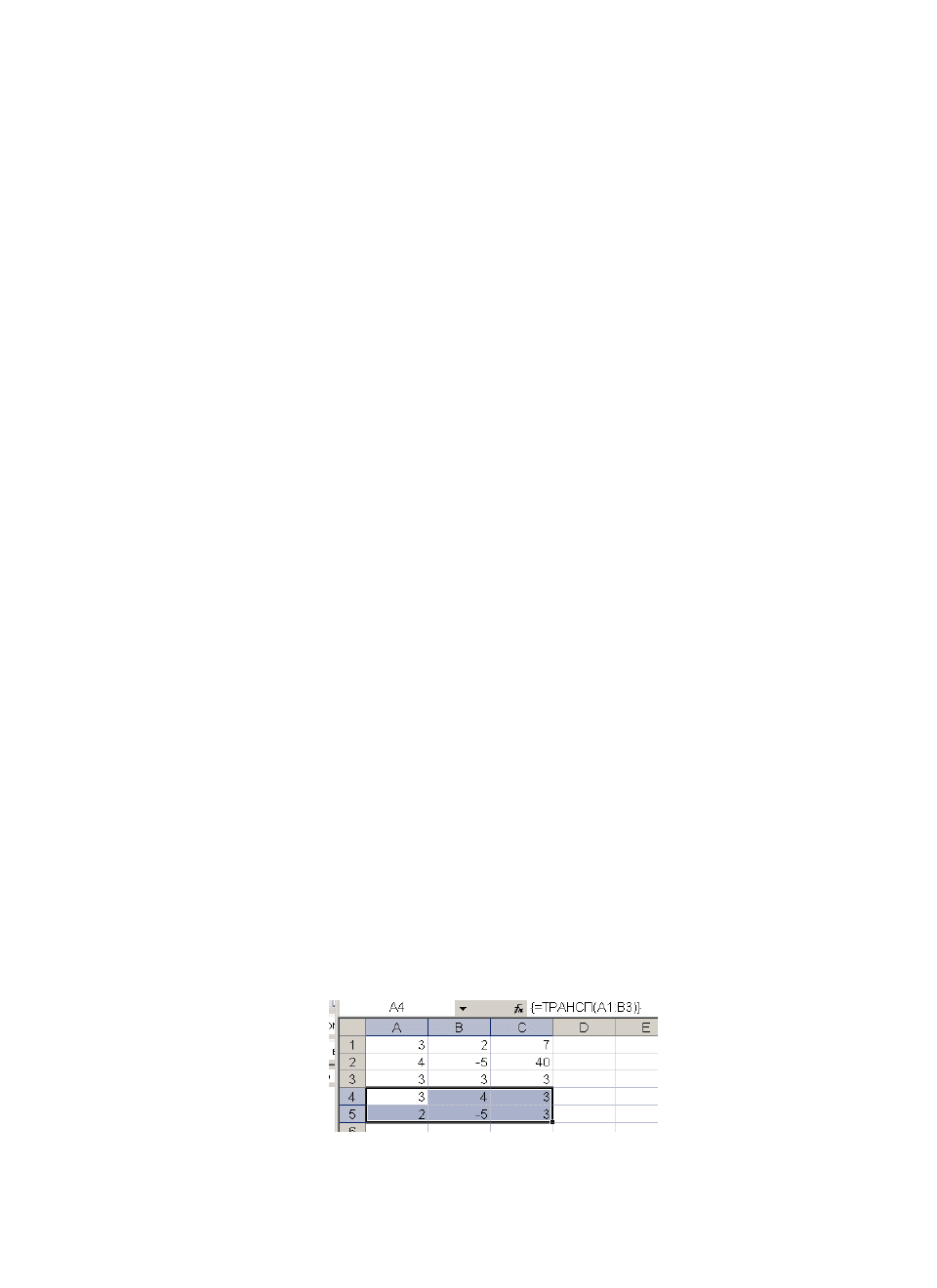
3) Найдем транспонированную матрицу А

с помощью функции ТРАНСП.

в диапазоне А4:С5 (рис.3.18)

Рис.3.18

4) Найдем произведение А

b в диапазоне Е4:Е5 (рис.3.19), оно равно (190,-

177)

;

Рис.3.19

5) Аналогично находим произведение А

А в диапазоне А7:В8

Рис.3.20

⎟

⎠

⎞

⎜

⎝

⎛

−

385

534

АА

6) Находим обратную матрицу ( А

А)

-1

. в диапазоне A10:B11

Рис.3.21

7) Теперь умножением обратной матрицы (А

А)

-1

на вектор А

b находим

вектор x.

В результате в диапазоне D1:D2 появится вектор решения системы по

методу наименьших квадратов. (рис.3.22). Причем х= 5 будет находиться в

ячейке D1, а у = -4 — в ячейке D2.