Ковалев Сергей. Программирование на алгоритмическом языке MQL4
Подождите немного. Документ загружается.

151
Код программы, реализующий этот алгоритм, выглядит так (compoundcondition.mq4):
//--------------------------------------------------------------------
// compoundcondition.mq4
// Предназначен для использования в качестве примера в учебнике MQL4.
//--------------------------------------------------------------------
int start() // Спец. функция start
{
double
Level_1, // Сигнальный уровень 1
Level_2, // Сигнальный уровень 2
Price; // Текущая цена
Level_1=1.2850; // Задаём уровень 1
Level_2=1.2800; // Задаём уровень 2
Price=Bid; // Запрашиваем цену
//--------------------------------------------------------------------
if (Price>Level_1 || Price<Level_2) // Проверка сложн услов
{
Alert("Цена находится за пределами диапазона");// Сообщение
}
//--------------------------------------------------------------------
return; // Выход из start()
}
//--------------------------------------------------------------------
Ключевым моментом в этом программном решении является использование сложного
условия в операторе if-else:
if (Price>Level_1 || Price<Level_2) // Проверка сложн услов
{
Alert("Цена находится за пределами диапазона");// Сообщение
}
Написанное простыми словами, это условие выглядит так: если значение переменной
Price больше значения переменной Level_1 или значение переменной Price меньше
значения переменной Level_2, то исполнять тело оператора if-else. Использование
логических операций (&&,|| и !) при составлении условий операторов if-else разрешено и
широко применяется в практике программирования (см. Логические операции).
При решении других задач может возникнуть необходимость составления ещё более
сложных условий, что вполне допустимо. При этом часть выражений может быть
заключено в круглые скобки, в том числе вложенные. Например, в качестве условия в
операторе if-else возможно использование такого выражения:
if ( A>B && (B<=C || (N!=K && F>B+3)) ) // Пример сложного условия
152
Таким образом, язык программирования MQL4 предоставляет широкие возможности для
использования операторов if-else: они могут быть вложенными, сами могут заключать
вложенные структуры, использовать простые и сложные проверочные условия, в
результате чего становится возможным составление простых и сложных программ с
разветвлённым алгоритмом.
7.3 Оператор цикла while
Наиболее мощным средством языка MQL4 является возможность организации циклов.
Довольно часто при создании прикладных программ приходится использовать
повторяющиеся вычисления, чаще это бывают одни и те же программные строки. Для
того чтобы программирование было удобным, а сама программа - понятной, используются
операторы циклов. В составе MQL4 имеется два оператора цикла - while и for. Здесь мы
рассмотрим первый из них.
7.3.1 Формат оператора while
Полноформатный оператор цикла while состоит из заголовка, содержащего условие, и
исполняемого тела цикла, обрамлённого фигурными скобками.
while ( Условие ) // Заголовок оператора
цикла
{ // Открывающая фигурная
скобка
Блок операторов, // Тело цикла может
состоять ..
составляющих тело цикла //.. из нескольких
операторов
} // Закрывающая фигурная
скобка
Если в операторе while тело цикла составляет один оператор, то фигурные скобки можно
опустить.
while ( Условие ) // Заголовок оператора
цикла
Один оператор, тело цикла // Тело цикла - один
оператор

153
7.3.2 Правило исполнения оператора while
Пока Условие оператора while является истинным: передать управление
первому оператору тела цикла, а после выполнения всех операторов тела
цикла передать управление в заголовок для проверки истинности
Условия.
Если условие оператора while является ложным, передать управление
оператору, следующему за оператором while.
Рассмотрим пример.
Задача 12. Вычислить коэффициент Фибоначчи с точностью до 10-го
знака.
Кратко охарактеризуем коэффициент Фибоначчи. Итальянский математик Леонардо
Фибоначчи обнаружил уникальную последовательность чисел:
1 1 2 3 5 8 13 21 34 55 89 144 233 ...
Каждое число в этой последовательности является суммой двух предыдущих чисел.
Представленная последовательность чисел обладает уникальными свойствами: отношение
любого числа к предыдущему равно 1.618, а к следующему - 0,618. Коэффициент 1.618
получил название коэффициента Фибоначчи, а указанная последовательность называется
последовательностью Фибоначчи (отметим также, что 0,3819 - сопряжённая величина для
коэффициента Фибоначчи, получена в результате его умножения на самого себя: 0.3819 =
0.618 х 0.618).
Задача состоит в том, чтобы вычислить коэффициент Фибоначчи более точно. Если
проанализировать коэффициент Фибоначчи для нескольких десятков элементов
последовательности, то становится очевидным, что полученные коэффициенты
колеблются вокруг иррационального числа 1.61803398875..., принимая поочерёдно то
большие, то меньшие значения. Чем большие числа из последовательности участвуют в
вычислениях, тем меньше отклонение от указанного значения.
154
Заранее неизвестно, какие именно числа необходимо взять, чтобы их коэффициенты
отличались между собой не более, чем в десятом знаке. Поэтому необходимо составить
программу, которая будет последовательно перебирать коэффициенты до тех пор, пока
разница между ними не окажется меньше 0.0000000001.
В данном случае для решения Задачи 12 создан скрипт (fibonacci.mq4), потому программа
не будет использоваться в длительной работе на каждом тике. После присоединения к
окну финансового инструмента скрипт должен один раз выполнить необходимые
вычисления (в том числе показать результат), после этого он будет выгружен из окна
клиентским терминалом.
//--------------------------------------------------------------------
// fibonacci.mq4
// Предназначен для использования в качестве примера в учебнике MQL4.
//--------------------------------------------------------------------
int start() // Спец. ф-ия start()
{
//--------------------------------------------------------------------
int i; // Формальн параметр,счётчик
double
A,B,C, // Числа последовательности
Delta, // Фактич. разница между Кф
D; // Заданная точность
//--------------------------------------------------------------------
A=1; // Начальное значение
B=1; // Начальное значение
C=2; // Начальное значение
D=0.0000000001; // Задаём точность
Delta=1000.0; // Начальное значение
//--------------------------------------------------------------------
while(Delta > D) // Заголовок оператора цикла
{ // Скобка начала тела цикла
i++; // Счётчик
A=B; // Следующее значение
B=C; // Следующее значение
C=A + B; // Следующее значение
Delta=MathAbs(C/B - B/A); // Искомая разница между Кф
} // Скобка конца тела цикла
//--------------------------------------------------------------------
Alert("C=",C," Число Фибоначчи=",C/B," i=",i);//Сообщение на экран
return; // Выход из start()
}
//--------------------------------------------------------------------
155
В начале программы производится объявление переменных (и даётся их описание). В
последующих строках переменным присваиваются численные значения. А, В и С
получают значения первых чисел последовательности Фибоначчи. Здесь необходимо
отметить, что, хотя в самой последовательности идёт речь о целых числах, частное от их
деления должно быть учтено в программе как действительное число. Если бы в данном
случае был использован тип int для этих чисел, то не было бы возможности вычислить
коэффициент Фибоначчи, например, 8/5 = 1 (целое число 1, то есть без дробной части).
Поэтому в данном случае использован тип переменных double. Собственно оператор
цикла выглядит так:
while(Delta > D) // Заголовок оператора цикла
{ // Скобка начала тела цикла
i++; // Счётчик
A=B; // Следующее значение
B=C; // Следующее значение
C=A + B; // Следующее значение
Delta=MathAbs(C/B - B/A); // Искомая разница между Кф
} // Скобка конца тела цикла
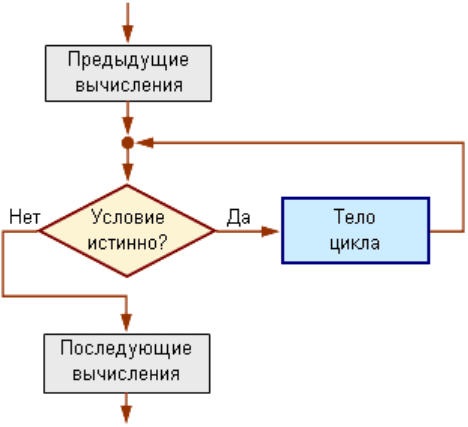
Рассмотрим функциональную схему оператора цикла while:
Рис. 42. Функциональная схема исполнения оператора while в программе fibonacci.mq4.
Оператор цикла начинает свою работу с проверки условия. Многократное выполнение
цикла будет повторяться до тех пор, пока условие (Delta>D) является истинным.
Понимание кода программы существенно упрощается, если при чтении операторов
произносить ключевую фразу - правило исполнения. Например, при чтении оператора
156
while это фраза: "До тех пор пока .., выполнять следующее: ..". В данном случае заголовок
оператора while звучит так: до тех пор, пока Delta больше D, выполнять следующее.. И
далее можно перейти к анализу программных строк, составляющих тело цикла и
исполняемых в случае истинности этого Условия.
Перед тем как управление в приведенном примере fibonacci.mq4 передано оператору
цикла while, значения этих переменных соответственно равны 1000.0 и 0.0000000001,
поэтому при первом обращении к оператору цикла условие является истинным. Это
значит, что после проверки условия управление будет передано первому оператору,
составляющему тело оператора цикла.
В данном примере - это оператор:
i++; // Счётчик
В трёх последующих строках вычисляются значения очередного набора элементов
последовательности:
A = B; // Следующее значение
B = C; // Следующее значение
C = A + B; // Следующее значение
Легко увидеть, что переменные принимают значения следующих (ближайших больших)
элементов. Если до исполнения оператора цикла значения А, В и С были равны
соответственно 1.0, 1.0 и 2.0, то в процессе первой итерации эти переменные принимают
значения 1.0, 2.0 и 3.0.
Итерация - повторное выполнение некоторых вычислений; используется для обозначения
факта исполнения программных строк, составляющих тело оператора цикла.
В следующей строке вычисляется интересующая нас разница между коэффициентами
Фибоначчи, полученным на основе последующих (C/B) и предыдущих (B/A) элементов
последовательности:
Delta = MathAbs(C/B - B/A); // Искомая разница между Кф
В этом операторе используется стандартная функция MathAbs(), вычисляющая
абсолютное значение выражения. Ранее указывалось, что по мере увеличения значений
элементов последовательности, коэффициенты Фибоначчи принимают поочерёдно то
большие, то меньшие значения, в сравнении с "эталоном". Поэтому разница между
соседними коэффициентами будет принимать то отрицательное, то положительное
значение. В то же время, нас интересует собственно величина этого отклонения, т.е. её

157
абсолютное значение. Таким образом, независимо от того, в какую сторону отклонилось
текущее значение коэффициента Фибоначчи, значением выражения MathAbs(C/B - B/A), а
также значением переменной Delta, всегда будет положительное число.
Этот оператор является последним в списке операторов, составляющих тело цикла, о чём
свидетельствует наличие в следующей строке закрывающей фигурной скобки. После
исполнения последнего оператора тела цикла управление передаётся в заголовок
оператора цикла для проверки условия. В этом состоит ключевой момент, определяющий
сущность оператора цикла. В зависимости от того, является ли теперь истинным условие
оператора цикла, управление будет передано либо на очередную итерацию в тело цикла,
либо за пределы оператора цикла.
На первых итерациях значение переменной Delta оказывается больше значения, заданного
в переменной D. Это означает, что условие (Delta > D) является истинным, поэтому
управление будет передано в тело цикла на следующую итерацию. Все переменные,
участвующие в вычислениях, получат новые значения, и после достижения конца тела
цикла управление снова будет передано в заголовок для проверки истинности условия.
Этот процесс будет продолжаться до тех пор, пока условие оператора цикла не станет
ложным. В момент, когда значение переменной Delta окажется меньше или равным
значению D, условие (Delta > D) перестанет соответствовать истине, а значит управление
будет передано за пределы оператора цикла, в строку:
Alert("C=",C," Число Фибоначчи=",C/B," i=",i);//Сообщение на экран
В результате на экране появится окно оператора Alert(), в котором будет напечатано
следующее:
С=317811 Число Фибоначчи=1.618 i=25
Это означает, что на 25-й итерации заданная точность достигнута, при этом максимальное
значение элемента последовательности Фибоначчи, которое было обработано, равно
317811, а сам коэффициент Фибоначчи, как и ожидалось, равен 1.618. Это сообщение
является решением поставленной задачи.
Здесь нужно заметить, что действительные числа в MQL4 вычисляются с точностью до
15-го знака. В то же время, коэффициент Фибоначчи отражён с точностью до 3-го знака.
Это произошло потому, что свойством функции Alert() является отображение чисел с
точностью до 4-го знака, но все последние ноли при этом не отображаются. Если бы у нас
158
возникла необходимость отобразить на экране число Фибоначчи с некоторой наперёд
заданной точностью, то нам пришлось бы несколько изменить код, например, так:
Alert("C=",C," Число Фибоначчи=",C/B*10000000," i=",i);// Сообщение
Особо нужно отметить следующее:
Возможна ситуация, при которой условие, указанное в заголовке
оператора цикла, всегда будет оставаться истинным, в результате чего
происходит зацикливание.
Зацикливание - бесконечное повторяющееся выполнение операторов, составляющих тело
цикла; критическая ситуация, возникающая в результате реализации ошибочного
алгоритма.
При зацикливании программа бесконечно исполняет блок операторов, составляющих тело
цикла. Вот простой пример оператора цикла while с зацикливанием:
int i=1; // Формальн параметр (счётчик)
while (i > 0) // Заголовок оператора цикла
i++; // Увеличение значения i
В данном примере происходит накапливание (увеличение значения) переменной i на
каждой итерации. В результате условие никогда не станет ложным. Аналогичная ситуация
возникает в случае, когда в теле цикла вообще ничего не вычисляется. Например, в этом
коде:
int i=1; // Формальн параметр (счётчик)
while (i > 0) // Заголовок оператора цикла
Alert("i= ",i); // Сообщение на экран
значение переменной i в цикле не изменяется. На каждой итерации на экран будет
выводиться сообщение:
i= 1
Этот процесс будет повторяться бесконечно. Однажды попав в ловушку зацикленного
кода, управление уже не может выйти из него. Особенно опасна эта ситуация в
торгующих экспертах и скриптах. В таких случаях обычно не обновляются переменные
окружения, т.к. специальная функция не заканчивает свою работу, а о факте зацикливания
159
пользователю может быть ничего не известно. В результате управление в выполняемой
программе не может быть передано в соответствующие программные строки, где
принимается решение о закрытии или открытии ордеров.
Задача программиста состоит в том, чтобы не допустить возникновение условий, при
которых неконтролируемое зацикливание становится возможным. Не существует метода,
с помощью которого можно было бы обнаружить эту ситуацию программным способом
ни на этапе компиляции программы, ни при её выполнении. Единственным возможным
средством для выявления подобных алгоритмических ошибок является внимательный
анализ кода - логические рассуждения и здравый смысл
7.4 Оператор циклa for
Вторым оператором цикла является оператор for.
7.4.1 Формат оператора for
Полноформатный оператор цикла for состоит из заголовка, содержащего Выражение_1,
Условие и Выражение_2, и исполняемого тела цикла, обрамлённого фигурными скобками.
for (Выражение_1; Условие; Выражение_2) // Заголовок оператора
цикла
{ // Открывающая фигурная
скобка
Блок операторов, // Тело цикла может
состоять ..
составляющих тело цикла //.. из нескольких
операторов
} // Закрывающая фигурная
скобка
Если в операторе for тело цикла составляет один оператор, то фигурные скобки можно
опустить.
for (Выражение_1; Условие; Выражение_2) // Заголовок оператора
цикла
Один оператор, тело цикла // Тело цикла - один
оператор
160
Допускается отсутствие Выражения_1, Условия и Выражения_2. При этом наличие
разделяющего знака ; (точка с запятой) обязательно.
for ( ; Условие; Выражение_2) // Отсутствует
Выражение_1
{ // Открывающая фигурная
скобка
Блок операторов, // Тело цикла может
состоять ..
составляющих тело цикла //.. из нескольких
операторов
} // Закрывающая фигурная
скобка
// - ------------------------------------------------------------------------
---------
for (Выражение_1; ; Выражение_2) // Отсутствует Условие
{ // Открывающая фигурная
скобка
Блок операторов, // Тело цикла может
состоять ..
составляющих тело цикла //.. из нескольких
операторов
} // Закрывающая фигурная
скобка
// - ------------------------------------------------------------------------
---------
for ( ; ; ) // Отсутств. Выражения
и Условие
{ // Открывающая фигурная
скобка
Блок операторов, // Тело цикла может
состоять ..
составляющих тело цикла //.. из нескольких
операторов
} // Закрывающая фигурная
скобка
7.4.2 Правило исполнения оператора for
