Ковалев И.В., Волкова Г.В. Автоматизированные системы конспект лекций

Подождите немного. Документ загружается.

директивные сроки начала

и окончания

. Для того, чтобы задача была

корректной необходимо выполнение условий

≤

(j)≤

(j)-

где K

– длина критического пути в q-м проекте плана, K

(j) – максимальный

путь из начального события в событие j.

Планируемый период

 

нoн

TTT min,, 

= max

разбивается на f интервалов

каждый (к=

fI ,

). На к-й интервал для каждого вида используемых ресурсов

заданы наличное их количество

и суммарная трудоемкость





. Кроме

того, считаются известными следующие функциональные зависимости

),),(,),((),(),(

qoqнq

jitjitjiwjiw 

),),(,),((),(),(

qoqнq

jitjitjinjin 

),),(,),((),(),(

qoqнq

jitjitjicjic 

где

jiw ),(

jin ),(

jic ),(

– соответственно, трудоемкость, среднее

количество используемых ресурсов и полезные трудозатраты в стоимостном

выражении, относящиеся к той части продолжительности работы

jit ),(

, которая

покрывается результатом τ



qн

jit ),(

– моменты начала и окончания работ.

Поскольку состояние процесса формирования в произвольный момент времени

определяется значениями

qн

jit ),(



i,j



,то последние можно

рассматривать как фазовые координаты объекта управления.

Требуется найти такую точку фазового пространства, т.е. значения

qн

jit ),(



i,j



, чтобы с учетом всех ограничений достигались номинальная, и по

возможности, равномерная загрузка всех видов ресурсов на протяжении

планируемого цикла.

2. Алгоритмизация модели

Сформулированную выше задачу формализуем в следующем виде. Движение

объекта в фазовом пространстве должно удовлетворять ограничениям на сроки

выполнения процессов

,)),(),((

),(

max

jit





(3.39)

NqDjit

нqн

Vji

,1,),(min

),(





и ограничениям на порядок выполнения задач, задаваемых топологией сетевых

моделей (комплексом информационно и по управлению взаимосвязанных задач

ИУС)

Nq ,1

, (3.40)

где J

– множество вершин (событий) сетевой модели.

Пусть R

– подмножество тех задач, которые покрываются к-м интервалом

времени длительностью τ



, к=

fI,

, R

1

120

На подмножестве

так называемая задача многотемного сетевого

планирования с учетом условий (3.39) и (3.40) представляется в виде целочисленной

модели.

max,),(),(

),(

)( 









jix

jic



(3.41)

,,,),(),(

),(

LIl

jix

w 









(3.42)

где













случае. противном в,0

интервале, м-k на явыполняетс),(,1

),(

jiесли

jix

)(l



– функция штрафа, о которой подробнее будет сказано ниже.

Для оптимального управления на всем планируемом периоде

 

oн

TT ,

требуется

оптимальность этого управления на любом интервале τ



Следовательно,

эффективность управления на всем планируемом периоде будет определяться

целевой функцией вида

Vji

jixjicl

),(),()(

),(

1 1

 





 



(3.43)

Задача (3.39) - (3.43) наиболее полно учитывает специфические особенности

процессов в ИУС. Максимизация функционала (3.43) эквивалентна минимизации

себестоимости выполнения всех операций.

В настоящее время для решения задач оптимизации сетевых моделей

применяются два метода: старый и испытанный алгоритм Д.И. Голенко [44],

использующий метод статистического моделирования в сочетании с методом

направленного случайного поиска и, сравнительно недавно предложенный

алгоритм, основанный на комбинации метода статистического моделирования и

точного метода неявного перебора – "ветвей и границ".

К недостаткам алгоритма Д.И. Голенко можно отнести следующее:

 применение метода статистических испытаний при наличии большого

числа сложных ограничений (см. (3.39), (3.40), (3.42)) требует значительных затрат

машинного времени;

 при нарушении в процессе поиска ограничений (при выходе из

допустимой области поиска) возврат осуществляется также методом статистических

испытаний;

 направленный случайный поиск осуществляется с постоянным шагом,

либо монотонно убывающим шагом, что мало эффективно при наличии сильной

овражности (использование штрафных функций необходимо влечет за собой

появление овражности) и многоэкстремальности оптимизируемой функции.

Ниже, для решения выше сформулированной задачи, предлагается алгоритм

случайного поиска с пересчетом с переменной величиной шага, который

осуществляет направленный поиск как при достижении допустимой области поиска,

определяемой заданными ограничениями, так и непосредственно в допустимой

области.

121

Поиск ведется в М-мерном пространстве, где





MMM

– число операций в

q- м плане) пространстве T – значений; t

(i,j)– начала всех работ.

Опишем процедуру поэтапно.

3. Многоэтапная процедура оптимизации сетевой модели

Этап I. В соответствии с топологией сети (3.40) и известными t

рн

(i,j)

и t

по

(i,j)

рассчитываем длину критического пути в каждом проекте плана операций – k

, а

также резервы времени всех работ

P(i)

= t

по

(i,j)

- t

рн

(i,j)

qн

kDD 

Nq ,1

Вычисляем Ш

iP )(max

(величина шага). Здесь максимум определяется по

всем работам, входящим в N рассматриваемых проектов.

Этап II. Определяем начальную точку поиска Т

(положение начал операций

проектов) по правилу



jit ),(

рн

(i,j)

iP )(



(i,j)

Nq ,1

Этап III. Проверяем выполнения условия (3.42) в найденной точке для каждого

k-го интервала

fIk ,

, т.е. выполнение требования о том, чтобы ожидаемая

потребная трудоемкость не превышала наличную по каждому виду ресурса (

LIl ,

)























случае противном в,1

),(

,,1,),(,),(),( если,0

jix

jiw



Этап IV. На этом этапе производится подсчёт интервалов, на которых условие

(3.42) не выполняется, определяется

Целочисленная функция  является

функцией качества при достижении допустимой области. Шаг считается удачным,

если значение  в новой точке меньше, чем в предыдущей.

Если   0, т.е. допустимая область ещё не достигнута, то переходим к этапу

VIII, если   , т.е. найденная точка находится внутри допустимой области, то

переходим к вычислению функции качества (3.43).

Этап V. В функционале (3.43)









– функция штрафа за невыполнение

условия











jix

jin

),(

),(),(

(3.44)

LIl ,

fIk ,

, которое обозначает, что наличное количество l –го вида

ресурса в произвольный момент времени устанавливается с некоторыми допусками





и 



122









Функция









определяется по формуле:









=1-



 







)(

kiill

tstsb



 









kiill

tstsb



)()(

где t

– моменты времени, в которые происходит изменение потребного кол-ва

ресурса (t

= t

(i,j)

или t

= t

(i,j)

+ t(i,j)

Nq ,1

);

)(

– суммарное количество l-го

вида ресурса, требуемого в момент времени t

;



– сумма по тем t

,в которых

происходит нарушение условия (3.44) справа (перегрузка);

– коэффициенты

штрафа за недогрузку и перегрузку соответственно, I

– число моментов t

на k-м

интервале -



Значение F

=F(T

) запоминаем и переходим этапу VI. Если



≥ I (



- номер

шага поиска), то переходим к этапу Х.

Этап VI. На этом этапе моделируем М-мерный единичный случайный вектор



(





), равномерно распределенный по всем направлениям фазового

пространства. Обозначим через

 

ji,



координату этого вектора, соответствующую

операции

 

ji,

в q-м плане проекте.

Этап VII. Переходим из точки T

в точку T

η+1

по формулам



















;),( ),(),( или

),(),(),( е сли ,),(

;),(),(),(),( если ,),(),(

),(

по

jiШ

рн

jiШ

по

jiШ

рн

jiШ

















































.случае противном в ,,1,),( ,),(),( (

),(

max

)),(),((

),(

max),(

если ,),(

),(

jit

рн

jit

рн





Для того, чтобы можно было осуществить возврат в точку Т

, вычисляются

величины

,,1,),(,),(),(),(

Nqjijitjitji

qqнqнq









которые хранятся в памяти до следующего шага. Переходим к этапу III.

Этап VIII. Если функция  вычисляется в первый раз, что случается либо в

начале поиска, либо после того, как вычислялась функция качества (3.43) (алгоритм

работал в допустимой зоне), то присваиваем 

значение  (

= ) и переходим к

этапу VI. В противном случае формируем новую величину шага по формуле























).()(),(),()(, если ,

);(),()(, если ,)(

);()( и если ,)(

);()( и или )( и если ,

100

101-

001















ШHШ

УШ

HУ(Δ(Ш

(3.7)

Здесь У(Δ) – число удачных подряд шагов, δ(Δ) – целое, наперед заданное

число, которое определяет, сколько необходимо сделать подряд удачных шагов для

того, чтобы величина шага увеличивалась, α(Δ) > I – коэффициент увеличения шага;

Н(Δ) – число неудачных подряд шагов, χ(δ) – целое, наперед заданное число,

123

определяющее количество неудач, после которого следует уменьшение шага, β(Δ)>I

– коэффициент уменьшения шага;

ε(Δ) – заданная точность, делать шаг меньше которой не имеет смысла; целое

число



(Δ) определяет сколько раз шаг уменьшался до заданной точности, если



(Δ)



(Δ), которое задается заранее, то поиск прекращается и точка





принимается за

оптимальную.

Если заранее известно, что оптимизируемая функция является унимодальной,

поиск можно прекращать сразу, после того, как величина шага станет меньше

заданной точности



(Δ). В противном случае, многократное (



(Δ) раз) увеличение

шага до Ш

при уменьшении его до



(Δ) позволяет избежать окончания поиска в

локальном экстремуме. При удачном шаге ( < 

) значение Н(Δ) обнуляется и

происходит переход к этапу VI; при неудачном (  

) – обнуляется У(Δ) и

происходит переход к этапу IX.

При попадании в допустимую область поиска (этап V) обнуляется как У(Δ), так

и Н(Δ). Для достижения большей надежности поиска можно при этом обнулять и



(Δ).

Этап IX. На этом этапе происходит возврат в исходную точку по формуле

Nqjijijitjit

qqqнqн

,1,),(,),(),(),(









и переход к этапу VI.

Этап X. На этапе вновь полученное значение функции качества F(T



)

сравнивается со значением, хранимым в памяти в качестве наилучшего – F

формируется величина шага поиска в допустимой зоне.

Если F(T



)>F

, то шаг считается удачным и F

присваивается значение F(T



), в

противном случае шаг считается неудачным и значение F

остается без изменения.

Таким образом, в памяти у нас постоянно хранится значение F

– наилучшее из всех

полученных в процессе поиска.

Величина шага формируется по правилу, аналогичному (3.45)























).()(),()(),()(, если ,

);()(),()(,)( если ,)(

);()( и )( если ,)(

);()( и или )( и )(если ,

100

101-

001

FFFШFFFHF)F(TШ

FШFFFHFTFШF

FFУFTFШF

FFHF)F(TFУ(F)FT FШ















где все параметры имеют тот же смысл, что и в (3.45). В зависимости от

специфики конкретной задачи значения параметров при поиске вне допустимой

области и при поиске в допустимой области могут задаваться различными.

Если шаг был удачным, то переходим к этапу VI, в противном случае к этапу

IX. При



(F)=



(F) и в качестве оптимальной принимается точка (совокупность

моментов начал всех операций в ИУС t

(i,j)

Nq ,1

; соответствующая F

, которая

хранится в памяти вместе со значением T

Таким образом, применение многоэтапной процедуры оптимизации позволяет

для имеющихся наборов величин t

(i,j)

, соответствующих оптимальному плану

процесса с учетом продолжительности всех операций – t(i,j)

рассчитать сроки

окончания операций t

(i,j)

В результате полностью определяется оптимальный

124

план, то есть формируется оптимальное расписание выполняемых в ИУС операций,

объединенных общими ограничениями на ресурсы.

Тема 3.7 Алгоритмическая GERT-процедура определения нормативных времен

выполнения параллельных процессов в условиях неопределенности

В качестве формальной базы алгоритмической GERT-процедуры используется

аппарат стохастических сетей и графического метода оценки и пересмотра планов.

До сих пор мы рассматривали лишь те модели реализации параллельных

процессов, которые описываются детерминированными сетями. Для полного

выполнения типичной сети такого класса необходимо выполнение всех дуг. Из

этого условия следует, что в такую модель не могут быть включены операции с

обратной связью, поскольку они представляются петлями, существование которых в

свою очередь означает, что конечный узел операции должен быть выполнен раньше

ее начального узла. В области детерминированных сетей наиболее полно были

изучены две модели. В первой из них, модели критического пути, время выполнения

каждой дуги фиксировано. Во второй, модели PERT, для каждой дуги существует

несколько возможных времен ее выполнения.

При моделировании работы промышленных автоматизированных комплексов и

информационно-управляющих систем нередко наиболее гибкими и полезными

оказываются сетевые модели со стохастической структурой. Стохастическую сеть

определим, как сеть, которая может быть выполнена только при выполнении

некоторого подмножества дуг; при этом время выполнения каждой дуги выбирается

в соответствии с вероятностным распределением. В стохастических сетях для

выполнения узла не является необходимым выполнение всех дуг, входящих в него.

Поэтому в таких моделях допускается существование циклов и петель.

1. GERT-сетевое представление моделей процессов

Узлы стохастической сети могут быть интерпретированы, как состояния

системы, а дуги — как переходы из одного состояния в другое. Такие переходы

можно рассматривать как выполнение обобщенных операций, характеризуемых

плотностью распределения, или функцией массы, и вероятностью выполнения.

Каждый внутренний узел стохастической сети выполняет две функции, одна из

которых касается входа в узел, а другая — выхода. Обычно эти функции называют

входной и выходной.

1. Входная функция. Она определяет условие, при котором узел может быть

выполнен.

2. Выходная функция. Она определяет совокупность условий, связанных с

результатом выполнения узла. Другими словами, с помощью выходной функции

указывается, должны ли выполняться все операции, которым данный узел

непосредственно предшествует, или только одна из них.

Отметим, что начальный узел сети выполняет только выходную функцию, в то

время как конечный узел—только входную. Существуют три типа входных

функций.

125

Определим следующие типы входных функций:

Тип 1. Узел выполняется, если выполнены все дуги, входящие в него.

Тип 2. Узел выполняется, если выполнена любая дуга, входящая в него.

Тип 3. Узел выполняется, если выполнена любая дуга, входящая в него, при

условии, что в заданный момент времени может выполняться только одна дуга.

Определим следующие типы выходных функций:

Тип 1. Все дуги, выходящие из узла, выполняются, если этот узел выполнен.

Данная функция называется детерминированной выходной функцией.

Тип 2. Ровно одна дуга, выходящая из узла, выполняется, если узел выполнен.

Выбор такой дуги может быть описан с помощью вероятности. Поэтому эта

функция называется вероятностной.

В настоящем разделе мы рассматриваем два типа узлов: а) узлы с третьим

типом входной функции и детерминированной выходной функцией и б) узлы с

третьим типом входной функции и вероятностной выходной функцией. Сети,

содержащие только эти два типа узлов, называются GERT-сетями. Для GERT-узлов

используются обозначения, приведенные на рисунке 3.27.

а) б)

а – детерминированный выход; б – вероятностный выход

Рисунок 3.27 – Типы GERT-узлов:

Покажем, как можно воспользоваться этими обозначениями при рассмотрении

простой ИУС технологического контроля и диагностики качества продукции

(рисунок 3.28). В результате выполнения операции проверки система контроля и

диагностики определяет, какие детали следует сдать в металлолом, какие исправить,

а какие отправить на линию сборки. После исправления детали могут быть проданы

в розницу, сданы в металлолом или отправлены непосредственно на линию сборки.

Рисунок 3.28 – Пример GERT-сети

126

Отметим, что р

+ р

= 1 и р

+ р

= 1. Кроме того, дуги (4, 2), (1, 4), (1,

2), (1, 3), (4, 3) и (4, 5) соответствуют физическим процессам, которые можно

описать плотностями распределения. Например, случайные величины,

соответствующие операциям (1, 4) и (4, 5), могут быть нормально распределенными,

операциям (1, 2) и (4, 3) — экспоненциально распределенными, а операциям (1, 3) и

(4, 2) — равномерно распределенными. Методы системы GERT позволяют ответить

на следующие вопросы:

1. Какова вероятность того, что деталь будет сдана в металлолом?

2. Какова вероятность того, что деталь будет использована на линии сборки?

3. Какова вероятность того, что деталь поступит в розничную продажу?

4. Чему равны математическое ожидание и дисперсия времени, необходимого

для изготовления детали, которая поступает на линию сборки?

5. Сколько времени будет потеряно, если деталь сдается в металлолом?

Далее предлагается аналитический подход, позволяющий ответить на эти

вопросы. Для его реализации необходимо рассмотреть основные процедуры

системы GERT. В качестве модели процесса будем рассматривать сеть G = (N, А),

содержащую только GERT-узлы, которые образуют множество N. Пусть время

выполнения операции (i, j) есть случайная величина Y

. По определению операция

(i, j) может быть выполнена только в том случае, если выполнен узел i. Поэтому для

изучения вопросов, связанных с выполнением этой операции, необходимо знать

условную вероятность (в дискретном случае) или плотность распределения (в

непрерывном случае) случайной величины Y

при условии, что узел i выполнен. Это

в свою очередь позволит нам провести исследования, связанные с выполнением

всей сети. В частности, мы сможем определить моменты распределения времени

выполнения сети, с помощью которых будут вычислены математическое ожидание

и дисперсия времени выполнения сети и соответствующего ей процесса.

Таблица 3.9 – Моменты и производящие функции моментов

Тип

распределения

(s)

Математическое

ожидание

Второй момент

Биномиальное

(В)

(pe

+ 1 – p)

np Np(np + 1 – p)

Дискретное (D)

...



epep

sTsT

...

2211



TpTp

...



TpTp

Экспоненциаль-

ное (E)

















Гамма (GA)















1

)1(

bb 

Геометрическое

(GE)

pee

1

p

Отрицательное

биномиальное

(NB)

pee













1

pr )1( 

)1)(1(

rprpr 

127

Нормальное

(NO)

)2/1(



ssm



m m

+ σ

Пуассона (P)

)1( 



λ λ(1+λ)

Равномерное

(U)

sba

sbsa

)( 



ba 

baba 

Пусть f

– условная вероятность или плотность распределения времени

выполнения операции (i, j). Условная производящая функция моментов случайной

величины Y

определяется как M

(s) = E[e

], т. е.

















величины) случайной дискретной (ддл )(

величины) случайной йнепрерывно (ддл )(

)(

ijij

yfe

dyyfe

В частности, M

(s) = E[e

] = e

при y

= a = const. Если a = 0, то M

(s) =1. В

таблице 3.9 описаны некоторые наиболее важные функции распределения и указаны

соответствующие производящие функции моментов и первые (математические

ожидания) и вторые моменты относительно начала координат.

Пусть p

— вероятность того, что операция (i, j) будет выполнена при условии,

что узел i выполнен. Для случайной величины Y

определим W-функцию как

(s) = p

(s) (3.46)

С помощью преобразования (3.46) всегда можно определить сеть G', структура

которой идентична структуре сети G, только вместо двух параметров дуг p

и y

присутствует один параметр W

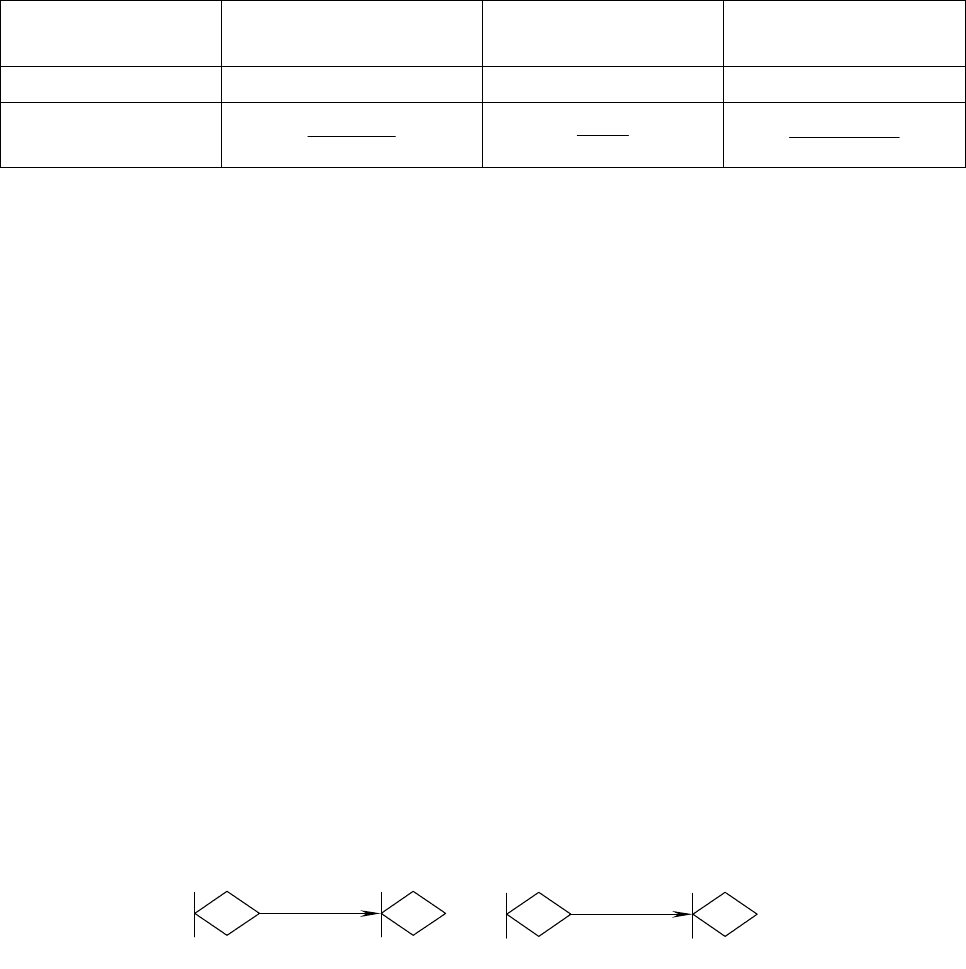
. На рисунке 3.29 изображены дуга сети G и

соответствующая ей дуга сети G'.

Wij=p

а б

а – элемент сети G; б – элемент сети G'

Рисунок 3.29 – Сети G и G'

В описание системы GERT мы включили в качестве параметра дуги время

выполнения соответствующей операции.

В действительности можно рассматривать также любой характерный параметр

процесса, который обладает аддитивностью по дугам любого пути.

Если времена выполнения операций сети G представляются независимыми

случайными величинами, то G' обладает рядом свойств, представляющих интерес с

вычислительной точки зрения. Для изучения этих свойств мы рассмотрим три

частных случая 1) G' состоит из двух последовательных дуг; 2) G' — из двух

параллельных ветвей, 3) G' — из одной ветви и одной петли.

128

Последовательные дуги

Рассмотрим простую сеть, состоящую из двух последовательных ветвей. Эти

две ветви могут быть заменены одной эквивалентной им ветвью, как показано ниже.

Исходные ветви имеют W-преобразования W

(s) = p

(s), W

(s) = p

(s). W-

функция для эквивалентной ветви (i, k) имеет вид W

(s) = p

(s). Напомним, что

производящая функция моментов суммы двух независимых случайных величин

равна произведению производящих функций моментов этих величин. Тогда

поскольку p

= p

и M

(s) = [M

(s)][M

(s)], то

Wik(s) = [pijMij(s)][pjkMjk(s)] = Wij(s)Wik(s) (3.47)

Основной результат (3.47) может быть обобщен на случай трех и более ветвей:

W-функция для эквивалентной ветви равна произведению W-функций для

последовательных ветвей.

Параллельные ветви

Рассмотрим простую сеть, состоящую из двух параллельных ветвей. Доказано,

что эти ветви могут быть заменены эквивалентной ветвью. Пусть (i, j)—такая ветвь.

По определению W

(s) =p

(s). В этом cлучае p

= p

+ p

и M

(s) = [p

(s)

(s)]/(p

). Поэтому

 

)()(

)( sWsW

sMpsMp

ppsW

bbaa

baij



















(3.48)

Формула (3.48) также может быть обобщена на случай сетей, состоящих из трех

и более параллельных ветвей: W-функция для эквивалентной ветви равна сумме W-

функций для параллельных дуг.

Петли

Рассмотрим простую сеть, состоящую из одной петли и одной дуги. Она может

быть преобразована в эквивалентную сеть, содержащую только одну дугу.

Отметим, что рассматриваемая сеть может быть преобразована. Эта новая сеть

будет состоять из бесконечной последовательности параллельных цепей, каждая из

которых представляет собой совокупность последовательных ветвей. Поэтому

можно вначале каждую ее цепь свести к эквивалентной дуге, а затем эти дуги

преобразовать в сеть, состоящую из одной ветви, эквивалентную исходной системе.

Пусть (i, j) — ветвь, эквивалентная сети. Из (3.47) и (3.48) следует, что вес

ветви (i, j) равен W

= W

+ W

+ … = W

[1+





1m

]. Данное выражение, в

котором мы временно опустили аргументы W-функций, можно упростить, зная, что

биномиальный ряд (1—W

)

-1

раскладывается следующим образом:

129